动力电池SOC估算设计与方法概述

姚子欣

江苏联合职业技术学院常州刘国钧分院 江苏省常州市 213000

目前电动汽车在我国已经逐步普及，但是续航里程过短等问题也在严重制约着电动汽车的进一步发展，由于电池电量的精准估算直接影响着上述问题，而且作为电池管理系统当中是最重要也是最核心的功能之一。

1 电池剩余电量定义

一般电池剩余电量状态用SOC表示，也称荷电状态（State Of Charge），是指电池存储电量百分数[1]。SOC的数学定义式如下：

公式中，SOC为电池剩余电量百分比，Qr为当前电池剩余的电量，Qc为电池的额定容量。一般认为电池的额定容量等于剩余电量与已放出电池电量总和，此外还通常采用另外一种公式来表达SOC：

公式中，QI为最近的一次充放电中，已经放出的电量。

2 SOC估算需要考虑的实际问题

2.1 针对汽车安全性的问题

对于汽车而言，保证安全是第一位需要考虑的，因此SOC估算误差不能影响到车辆安全。在考虑设计SOC估算方法的同时必须考虑关于安全方面的几点：

（1）针对汽车安全性设置冗余。例如需要针对使用过一段时间的电机系统可能会出现的性能退化情况要有电量冗余或者在充电时，防止电池出现过充，当SOC估算出为95%时，也要显示为100%，实际上这样也减小了电池充放电的深度。

（2）电池管理系统必须设置另外一套不依赖于SOC的安全机制。原因如下：第一，将SOC估算值作为唯一指标，则估算误差会严重影响汽车安全；第二，SOC估算需要一定的时间和内存，当故障或事故发生时需要系统优先及时处理相关信息，而电池电量可以临时采用电压比较器来进行监测。

2.2 实现可行性的问题

SOC估算需要兼顾到系统的可行性，在一定条件下提高估算的精度，主要包括技术与成本两个方面：

（1）从软件算法出发，考虑技术的可行性。

SOC估算不能太过复杂，因为车用芯片的运算能力有限，内存空间不足，在考虑设计SOC估算的同时使系统随时有效地评估SOC。

（2）从硬件电路的角度，考虑成本的可行性。

SOC的精度有很大程度取决于对电池的温度、电压及电流的监测，若选择精度过高的传感器会导致成本过高，所以需要在硬件成本与精度之间进行取舍。

2.3 针对驾驶员需求的实际问题

SOC的另外一个作用是用于帮助驾驶员判断车辆的剩余行驶里程，因此需要考虑以下几个方面：

（1）显示信息量与准确性

考虑到驾驶员对SOC的百分数并不敏感，所以电池SOC在仪表显示一般为图形分度，这样更符合传统汽车驾驶员的习惯。

（2）考虑到驾驶员的主观感受

第一，对驾驶员显示的SOC值不允许跳变，因此显示精度并不非评判SOC估算的唯一指标。

第二，受算法的影响，SOC值可能会出现的回弹现象会导致驾驶员对系统不信任，所以SOC在放电时不允许出现电量增长的情况。

第三，在电池组放电末期，驾驶员对电量误差的敏感度提高，所以这是需要提高SOC的显示精度。

3 SOC的估算方式

3.1 以端电压为基础的方法

由于蓄电池都存在着电压迟滞现象，即电池的端电压不能迅速达到实际电压值[2]，需要保证蓄电池在一段时间内既不充电也不放电，此时电池内部达到稳定状态，那么电池端电压则为电池的静态电动势，由图1可看出，端电压与SOC有较为准确的对应关系。但是上述方式存在两点问题：（1）无法实时地准确估算电池SOC，因为在使用过程中无法留出足够的时间进行静置电压；（2）由于磷酸铁锂电池的电压平台过于平缓，所以会造成电压平台的一段区间内无法准确地对应出SOC，所以更常用于电压平台更加陡峭的三元锂电池[3]。开路电压法虽然存在一定的缺点，但是在误差范围内还是允许的，一般提高电压测试精度或提高电压采集分辨率可以有效地克服上述问题。

图1 单体电池端电压与容量关系曲线

3.2 以安时积分为基准的方法

该方法的理论基础为公式（2），通过过去参数QI可以估算出剩余电量。将放电电流函数i（t）与放电时间dt作积分处理后，考虑到充放电存在一定的效率η,得出时间段内的放电电量QI，再通过总容量Q就可以求得剩余电量的绝对值。

假设当t1时刻的电池剩余电量为Qt1，当前时刻t2电池的剩余电量为Qt2，计算从时间t1到t2电池总计充放电的电量为：

则

其中η为充放电效率，i（t）为电流关于充放电时间的数值函数，i（t）可取正或负值：当为放电时，i（t）取正值；当为充电时，i（t）取负值。结合公式2即可求出SOC。

安时积分法相较于第一种估算方法精度更加准确，但自身也有以下几种缺陷需要考虑：（1）电池的初始电量必须精确，若初始电量即上一次电量估算不准确就会带来新的估算偏差；（2）同样存在电流采集的累积误差问题，由于安时积分法主要通过电流传感器采集电流，那么电流传感器的精度就会直接影响电量的变化量[4]；（3）电池内部存在自放电即本身的电量会自行降低，且会贯穿电池的生命周期，所以采用安时积分法必须要考虑到这方面的问题。

3.3 电池端电压法结合安时积分法

考虑到安时积分法在动态计算电量变化值时的优点以及开路电压在静置时估算电量的优点，可以将两者的检查方法相结合，如图2为SOC的估算模型。

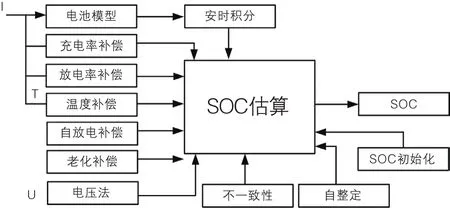
图2 SOC估算模型

该模型考虑到了电池的充放电补偿、电池工作温度的影响、老化影响、电池单体一致性以及自放电等问题，将影响因素折算为系数进行标定。此外通过进一步细化温度与SOC-OCV曲线，特别对放电末期的OCV值进行修正，较好地解决因其他因素带来过大的修正系数引发的SOC跳变等问题。

3.4 电池内阻法

由于电池内部存在浓差极化和活化极化等情况，这些情况导致了电池无论在充电还是放电时都会产生热量，所以一般认为电池内部存在内阻抗，且分为交流阻抗和直流阻抗。交流阻抗，表征对交流电的阻碍能力，可用交流阻抗仪来测量；直流阻抗表征对直流电的阻碍能力，一般通过电压变化量ΔV与电流变化量ΔI的比值来确定。部分文献通过大量实验表明电池SOC状态与交直流阻抗都有关系，实际上当电池老化过程中，容量在不断衰退，其内阻也在不断增加，所以一般用于电池中后期估算SOC。但是电池内阻法一般不用于磷酸铁锂电池，原因有以下几点：

第一，SOC不仅受到电池内阻的影响，同时还受到温度等因素的影响，两者的对应关系较为复杂，所以直接采用内阻对应SOC的方法并不准确。

第二，电池内阻的计量单位属于毫欧级，常规电路无法进行实时测量，且易受到电磁干扰。

第三，对于电池的一致性要求较高，如果单个模组内电池不一致性过大，将会对内阻的检测产生较大的错误，因此难以确定“内阻-SOC”曲线。

3.5 负载电压法

通过将电池短暂地静置后可视为电池处于开路状态，为了补偿电池端电压法存在的问题，考虑到电池都存在内阻，可将电池视为一个直流内阻模型如图3，电池的内阻r和工作电流I为已知的，只需测量负载RL两端的工作电压UL，可按照下述公式来计算电池端电压：

图3 电池组等效模型

上式中：EMF为电池电动势，UL为负载工作电压，r为电池的内阻，I为工作电流。上述方法在理论上是可行的，但依然存在一些缺点：

第一，例如磷酸铁锂电池内阻r与多种因素有关，且电池个体差异大难以准确获取。

第二，实际电动汽车运行过程中电流I的数值波动较大，会影响其计算结果。

第三，负载电压法最终要回归于计算OCV或EMF，因此也不能回避端电压法存在的一些缺陷。因此较少地用于车辆运行工况，但可用于电池充放电截止的判据。

3.6 卡尔曼滤波法

卡尔曼滤波法是当前较为热门的估算SOC的方式，该方式将电池充放电运行过程看成一个状态转换过程，状态由多个状态参数确定，包括了激励噪声和观测噪声等[5]。采用卡尔曼滤波估算电池SOC，精度可以提高到2%。根据其SOC定义式：

将SOC定义式和电池电压定义式进行线性处理再将其泰勒展开后再次迭代。这样SOC的预估校正过程可以消除更多的误差，但是对于电池单体的离散情况依然无法解决。

3.7 人工神经网络法

人工神经网络法属于人工智能方面的热点研究领域，通过模拟人的脑神经网络，建立大量网络节点，采集电池各个参数值并通过网络对应出电池实时的SOC，但是该方法需要建立在功能强大的芯片上才能实现，目前处于实验阶段。

4 总结与展望

SOC估算作为电池管理系统中最为重要的功能，也是当前电池管理系统（BMS）的研究热点之一，虽然SOC的估算方式有多种，但是每种方式都具有一定的局限性，与快速、高效以及低成本的要求还有一定的距离，所以需要考虑结合不同的方式以及影响电池SOC的各种因素等，对算法的结果进行修正，从而达到精准估算SOC的目的。