实验探究 助推几何难点的突破
2022-11-22江苏省江阴市周庄中学朱炎林
⦿江苏省江阴市周庄中学 朱炎林
几何证明题是学生学习的难点,几何图形变化的抽象性,常常让几何证明显得神秘又复杂,让学生一筹莫展.而解决几何证明难点的最好手段就是通过实验探究直观观察,通过自己动手实践,亲身体验图形变化的过程,突破思维的阻碍,获得结论.本文中以笔者的一节课为例,谈一谈如何通过实验探究,突破几何证明的难点.
1 教学分析
本课主要通过剪纸、画图和组题实验,让学生自己动手,了解图形的基本特征,体会图形经过平移、对称和旋转之后的分割与组合;通过图形组合,形成解决问题的思路,提高解决几何疑难问题的能力.
在教学中采取教师引导、学生探究、互动交流的方式进行学习,学生在探究与合作中,获得解决问题的路径;通过实验操作,学生由感性认识逐步上升到理性认识,归纳出解决几何疑难问题的思路和方法.
2 过程解析
2.1 导入
2.1.1 温故知新
师:同学们已经学习了哪些几何知识呢?
生:三角形、轴对称图形等.
师:同学们还记得轴对称图形的主要关键词吗?
生:对折.
师:是的.我们还学过判定三角形全等的各种方法,那么今天我们将采用实验探究的方法来进行进一步的学习.
设计意图:通过直接的对话,开门见山,直入主题,让学生对本节课要学习的内容做到心中有数.
2.1.2 动手实验,回顾知识
(1)请你将两张不同颜色的纸叠在一起,并按照图1所示进行剪裁.

图1
(2)请你将所剪的图形展开,并说一说这个图形有什么特征?(如图2)

图2
(3)将图1的最后一个图形按照图示(如图3)进行剪裁,再展开,说一说它的特性.

图3
设计意图:通过用不同颜色的纸叠加完成,增加趣味性,从视觉上引起学生的注意;通过动手实践和观察,学生能比较准确地说出图形的特征,增加了学生学习的信心.
2.1.3 设置疑问,激发学生的好奇心
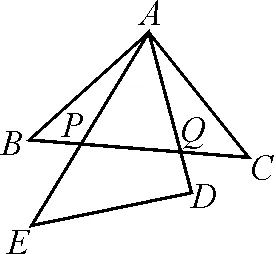
图4
问题如图4放置两个等腰直角三角板,将△AED绕点A进行旋转,AE,AD与△ABC的斜边BC相交于点P和点Q,请问以BP,PQ和QC为边的三角形为直角三角形吗?
设计意图:通过设置疑问,让学生带着疑问进入下面的学习,会紧紧抓住学生的注意力,让学生充满要解决问题的斗志.
2.2 实验探究
实验1按照图5所示剪纸,裁剪再进行折叠,将角进行平分.
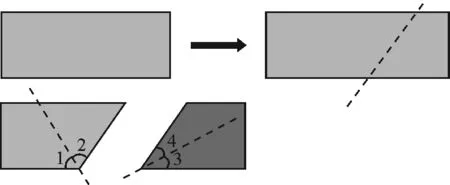
图5
设计意图:实验1从最基础的图形出发,让学生能快速入门,并感受到几何学习的简单和乐趣.
实验2将实验1中的任意两个剪纸进行组合,你可以画出多少种组合的图形?
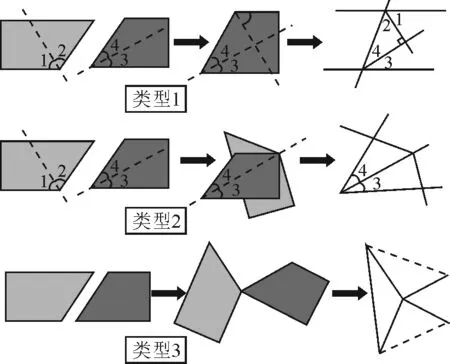
图6
设计意图:学生自己裁剪图形一开始可能出现毫无章法的现象,偏离课堂目标.教师要适时地进行引导,通过画出组合图形引导学生朝着平移、对折、旋转的思路入手.教师对于学生的尝试要及时给予肯定和表扬,并且可以鼓励学生小组合作,尝试多种组合方式(如图6所示).
2.3 合作探究
小组合作探究以下几何问题,每一组的要求不尽相同,小组之间展开良性竞争.分层施教,关注学生的个性发展,落实“以生为本”的教学理念.
(1)根据图7,提出几何问题.
设计意图:从最简单的问题入手,激发学生学习的信心,符合学生由浅入深的认知规律.
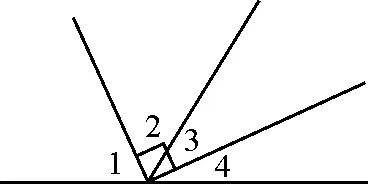
图7

图8
(2)图8是通过什么图形转换而来的呢?你能提出相关的几何问题吗?
60例患者一线、二线治疗后CR 3例(5.00%),PR 37例(61.67%),SD 12例(20.00%),PD 8例(13.33%),总缓解率为66.67%。其中一线治疗CR、PR、SD、PD各为2、22、7、3例,二线治疗CR、PR、SD、PD各为1、15、4、5例。一线治疗(70.58%)与二线治疗(61.54%)总缓解率无显著性差异(χ2=0.543,P>0.05)。总体无进展生存时间为(11.67±2.32)月,其中一线治疗为(12.43±2.41)月,与二线治疗(11.0±2.28)月无进展生存时间无显著性差异(t=2.330,P>0.05)。
设计意图:通过实物操作,抽象出图形的概念,初步渗透数学建模思想,实现思维的飞跃,促进思维的发展.
(3)图9又是如何得来的呢?
设计意图:由图8到图9,图形上只有微小的变化,实质上却是探究内容从平行线到等腰三角形和轴对称图形的扩展,设计的精妙之处也就在于此.
(4)将三个等腰三角形组合成如图10所示的汉字“区”或字母K的图形,那么这三个三角形有什么关系呢?

图9
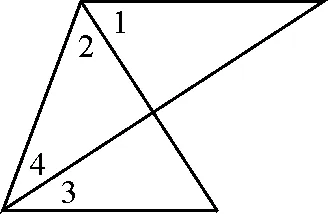
图10
设计意图:从图9到图10的变化,体现了从简单图形开始逐渐延伸到复杂图形,提高学生学习的深度,拓展思维的广度,提升学生的认知水平.
(5)如图11,将过点O的直线绕点O进行旋转,仔细观察图形,寻找图形之间的关系.
设计意图:通过开放型的设问,发展学生思维的发散性.教师要注意创造学生交流和思考的平台,鼓励学生进行分析、思考,培养学生自主解决问题的意识.
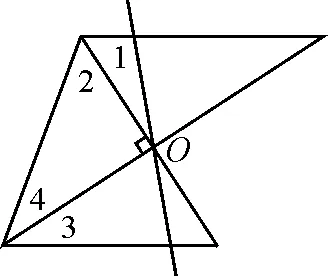
图11

图12
(6)仔细观察图12,请写出AD,BC和AB之间的关系,并说明你的理由.
设计意图:图12是在上述图形的基础上演变而来的,考查学生的知识迁移和转化能力.对于学生已经略有遗忘的知识,教师可以适当提示,帮助学生从复杂图形中分离出简单图形.

图13
(7)如图13,AD与BC平行,∠DAB和∠ABC的角平分线分别是AO和BO,CD的中点为O,AD和BC的和与AB相等.请你以上述四个条件中的任意三个作为条件,一个作为结论,写出不同的几何命题,并进行论证.
设计意图:本题是针对学习能力较强的学生进行的拓展,从一题多解、一题多变中进行思维训练,培养学生思维的灵活性.但是在实际教学中要注意不能对所有学生提同样的要求,否则一方面会造成课堂时间不够,另一方面也会导致学习能力稍弱的学生失去学习的信心.所以要做好分层要求,才能更好地提升学习效果.
2.4 解决疑难问题
学生提出在学习中遇到的疑难问题,共同解决.
设计意图:通过本课所学,引导学生遇到疑难问题时,该采用什么数学思想解决,应该从哪里开始着手等,让学生大胆地尝试,教师做好引导和纠正工作.
2.5 反思总结
小组合作进行本课的小结,谈谈本课的收获以及还有什么期待学习的问题,互相交流.
3 课后反思
3.1 取得良好教学效果的关键是完美的教学设计
教学设计是教师对整堂课的预设和把控,只有做出精准、完美的教学设计,才能保证课堂的教学效果.教学设计首先要根据课程标准和教材,确定准确合理的教学目标,并且能根据学情进行具体的调整和个性化的设计.当教师能把握教学的每个细节,那么离精彩的课堂教学就不远了.因此,教师要在教学设计上花时间和心血,做好课堂各个环节的安排,为顺利完成教学任务做好铺垫.
3.2 有效控制课堂讲解时间,合理调配教学时间
(1)试题要精讲精练.每道试题的选择要有目的、有设计,尽量控制好讲解的时间,给学生充分思考和展示的时间和空间.
(2)课堂难度安排适当.如果课程太简单,学生觉得毫无挑战,也不愿意去参与;如果教师随意发挥,思维过度跳跃,学生也很有可能因为跟不上节奏而消极“罢工”.因此,试题讲解难度要适中,注意由浅入深,深浅适度,并留有余地.
(3)课堂讲解要注意给学生留下交流的空间,让学生在交流中汲取经验,取长补短.
3.3 有效完成作业,提高课堂效率
课堂作业是对课堂所学知识的巩固,与课堂讲解相辅相成,缺一不可.学生能较好地完成课堂作业,才能有效提高学习效率.
(1)作业重质不重数,作业的安排要有针对性,能够对本课所学内容起到巩固、训练以及补充的作用,不做无意义的重复劳动.
(2)改变单一的作业形式,丰富作业的完成形式.传统的作业形式一般是书面作业,可以创新作业形式,如,口头问答、实验探究等.教师批改作业的形式也可以多种多样,如,同学之间互问互答,合作交流等.
(3)注意分层布置作业,关注个性发展.每个学生都有不同的特点,教师要尊重学生的个性差异,根据他们已有的知识经验和水平进行分类教学,分层要求,调动他们学习的积极性,发掘他们的潜能.在作业分层中不仅可以数量分层,也可以难度分层,目标分层,等等,为每位同学创设可以达到的目标.
总之,教学的内容、对象都决定了教学没有一致的可以照搬摘抄模板.教师只有遵循教育发展的规律,创造性地进行开发,用丰富的内容、多样的教学方式、精心设计的课堂结构让所有学生感受数学学习的快乐,学有所获!Z
