系统聚类分析法在学生成绩评价应用中的深度挖掘①
2022-11-22汤凤香方秀男康兆敏杨文泉
汤凤香, 方秀男, 康兆敏, 杨文泉, 李 东
(佳木斯大学理学院,黑龙江 佳木斯 154007)
0 引 言
学生成绩的评价问题一直是人们关注的焦点问题,即使是在大力提倡素质教育、人文教育的当下,学生成绩的高低仍然是衡量一个学生优劣的最直接的评价依据,因此如何根据学生的实际成绩尽可能客观、公平的评价学生,就显得尤为重要。从目前的实际情况看,学生的总成绩或是平均成绩,仍然在学生的成绩评价中占有重要的地位。此外,也有一些文献提出了学生成绩评价的方法,如层次分析法,主成分分析法,灰色预测法和模糊综合评价法等[1-5]。文献[6-7]是研究学生成绩综合评价问题的比较新的研究成果,其中[6]将权重分析与秩和比评价法相结合,在综合考虑分数与排名的基础上对学生成绩进行了综合评价;文献 [7]对各个影响因素进行主成分分析从而确定指标权重,基于成绩排名得到主成分得分,进而对学生成绩进行了综合评价。本文旨在文献[6-7]的研究基础上,尝试利用系统聚类分析的方法,对学生成绩评价做进一步的分析,并对不同方法得到的结果进行比较研究。 从已有的研究成果看,采用系统聚类法研究综合成绩评价的文献较少[8]。
1 系统聚类分析法概述

2 模型建立与求解
2.1 五种系统聚类方法的分类研究
数据来自于某中学学生9门课程的成绩,学生总人数1383人,其中一部分数据见下表:
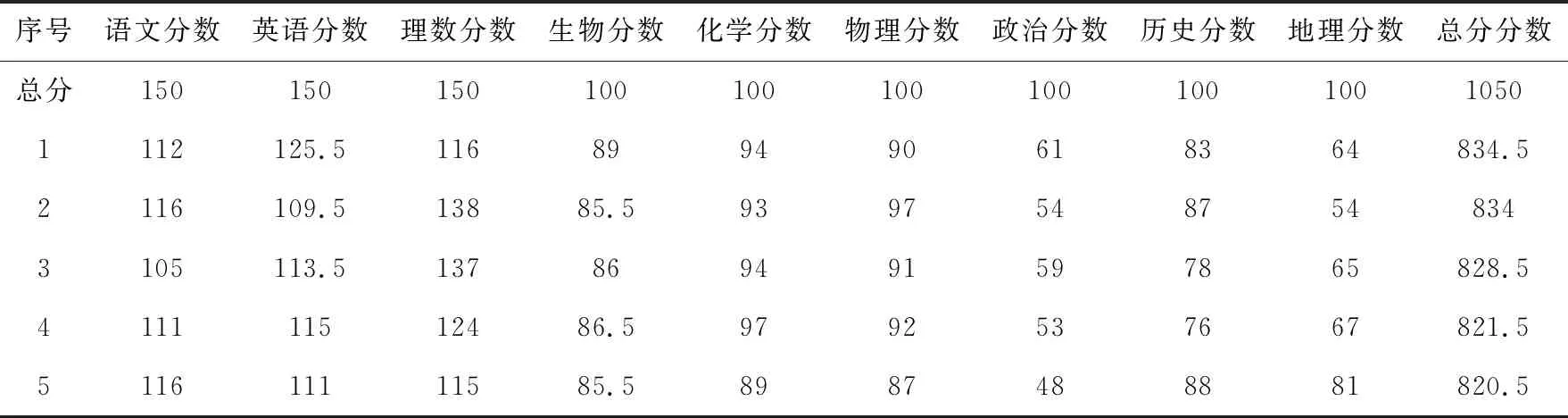
表1 学生成绩部分数据
利用MATLAB软件,并以前20个样本为例,打算分成六类,分别采用最短距离法、最远距离法、类平均法、重心法以及ward法等五种系统聚类方法得到如下分类结果:
从表中分类结果看,各个方法的分类结果有较大差异,从而对于分类决策造成一定困难。为此,对五种分类结果的相关性做进一步的研究,采用SPSS分析五种结果的相关性得到:
从结果可以看出,类平均法和其他几种方法相关性较好,其中类平均法和最短距离法有最好的相关性0.681,且显著性较强。除类平均法以外,其他几种方法之间的相关性很差。因而,最短距离法与类平均法的结果在某种意义上可以互相借鉴,并可以确定使用类平均法进行聚类分析。
2.2 分类数的合理性检验
利用分类的方法对样本进行评价研究时,分得类过少或者过多都有各自的弊端,这里不再赘述。那么将样本分成多少类合适?本文采用统计学当中的F检验方法,构建如下的统计量[9]:
其中u1,u2,…,un为n个样本,ui=(xi1,xi2,…,xim)含有m个指标,另外记
可以看到,类别从2类到10,分6类较合适,因F值从大到小然后到11.584第一次出现上升,然后又递减。而前面的2类和3类F值虽高,但类太少,因此确定最佳分类的方式即为F值递减后第一次出现上升趋势的值所对应的类数。
2.3 基于类平均法的分类及评价
从2.1中的结果可以看出,不同的聚类分析方法得到的结果是有差异的,而通常将不同的结果作为更多可能性的一种参考,但从实际最终决策的角度来说,更倾向于“少数服从多数”的原则。从五种方法的相关性分析结果来看,最短距离聚类和类平均聚类的结果是可以作为决策参考的。根据表2对比两个结果,第2、5、16、17个样本作为少数样本单独分类,单独比较这几个样本与其他样本的差距是不理想的,这里从几个类的聚类中心出发进行比较。以类平均法聚类为例,各类的聚类中心如下:

表2 五种聚类分类结果
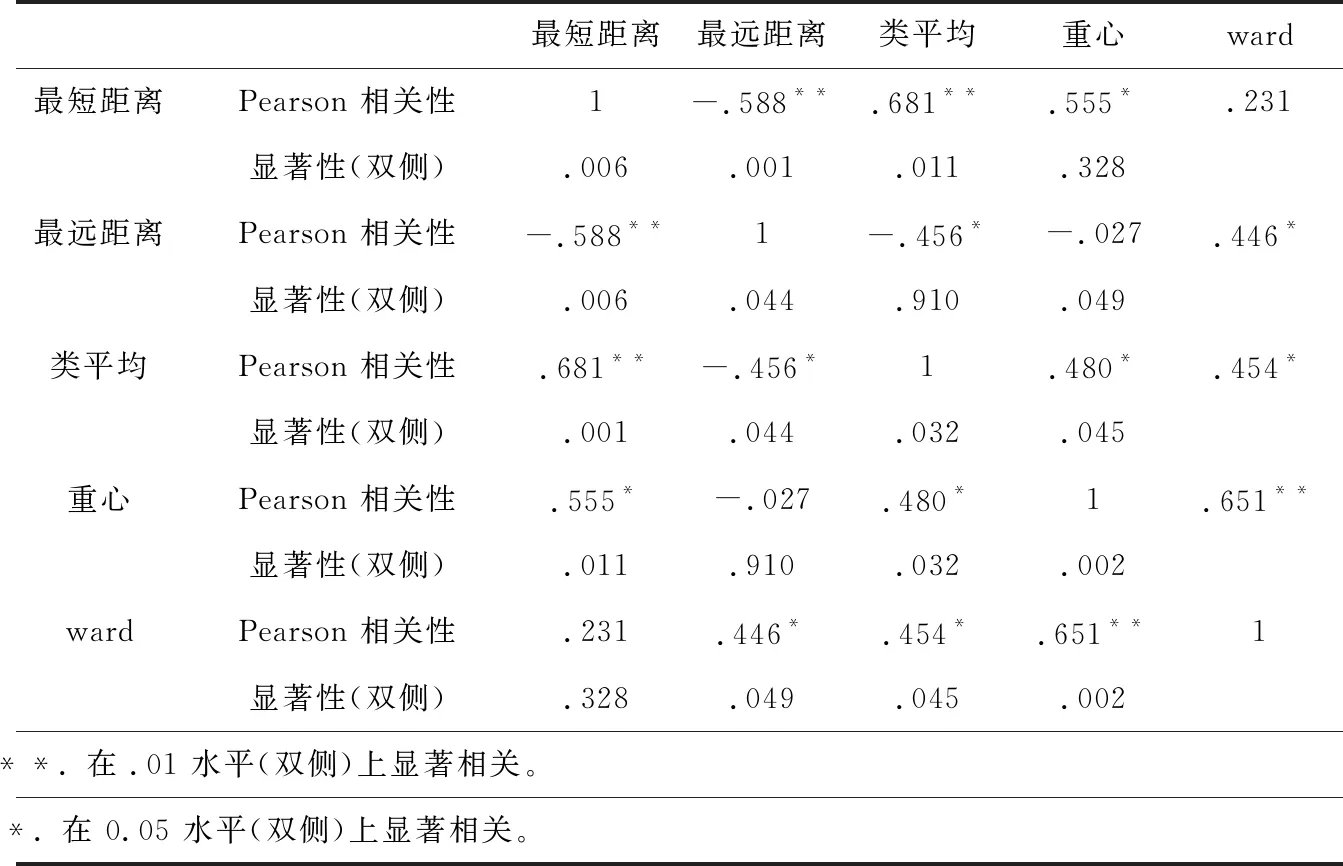
表3 五种聚类结果的相关性
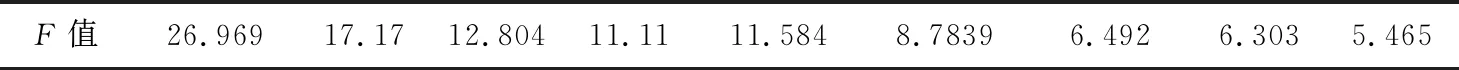
表4 类平均法各分类F值
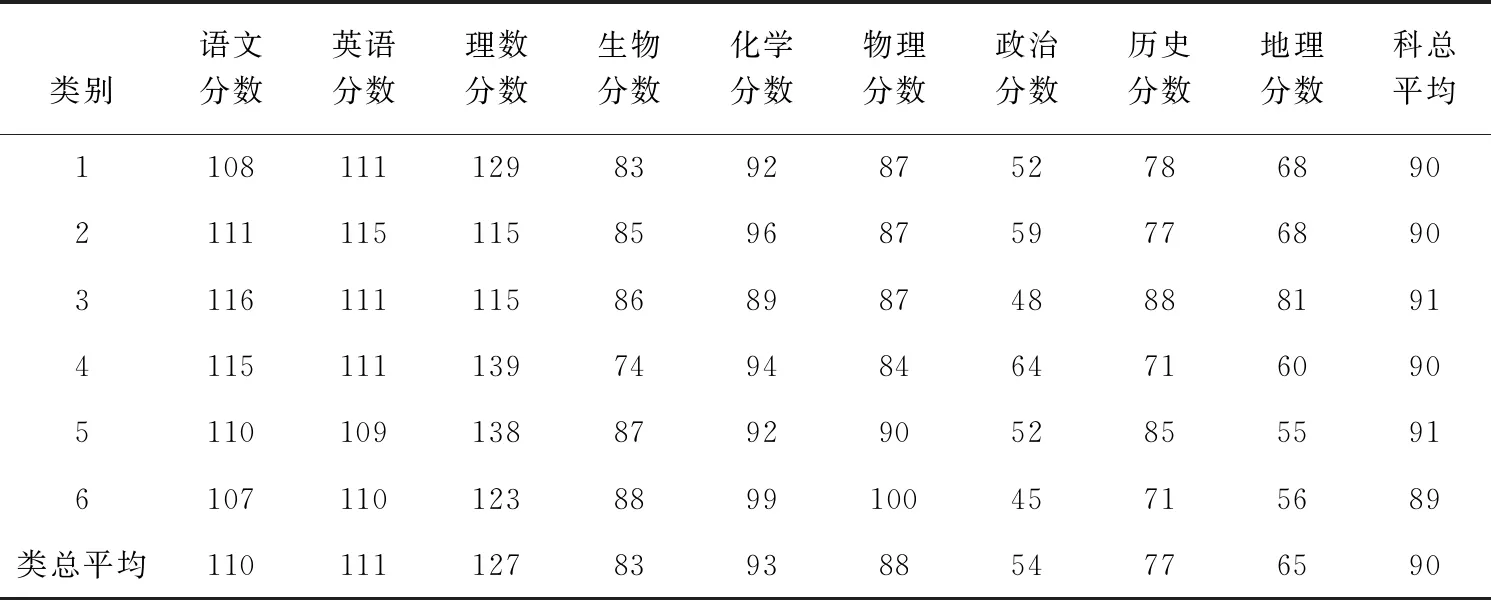
表5 类平均法各类的聚类中心
首先,选择的前20个样本的总成绩相差不大,因此如果单从总成绩来对他们进行分类是不恰当的,因为他们都很优秀,这一点从科总平均分差距不大得以验证。其次,第1个类别的学生人数较多达到了9名,因此第1类的类平均分与总体平均分非常接近,反映了这个总体的平均水平。最后,如何通过分类结果对成绩分布的特点进行发掘与说明?这一点可以从某一科目的平均成绩在不同的类当中是否变化明显得出一定的结论,例如以生物科目为例,其在第4类的分数为74分,明显低于其他类的分数,因此,可以初步认定第4类学生生物科目的成绩相对较弱。与之对应的,第3类学生地理科目的成绩明显高于其他类,因此初步判断第3类学生的地理成绩不俗。
3 结 语
对于学生的评价,单从分数上论显然是不全面的,例如考虑某种极端情形
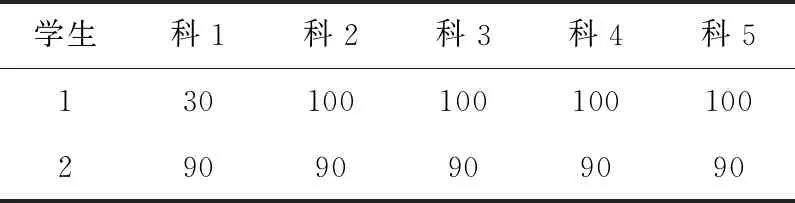
学生科1科2科3科4科513010010010010029090909090
显然单从成绩上来看,学生2的总分要高,但是学生1的四门课程均为满分。如果从某入学门槛来看,学生1单门课程不及格,极有可能导致这样的人被拒之门外,这是符合规则但是又不符合人才培养的常理的。研究希望为类似的选拔机制提供一个借鉴,根本目的是希望人才的选拔更加全面一些,减少因错过未来的人才而造成的损失。
