柔性路面层系统下瑞利波传播模式特性研究
2022-11-22肖展
肖展
(广西南宾公路建设发展有限公司,广西 南宁 530400)
0 引言
柔性路面广泛应用于各等级的道路和街道中,而随着道路运行时间持续、外界环境变化、材料内部温度变化和人为因素的影响,使道路质量产生相应问题,严重时甚至危害结构的安全。因此,道路网的维护与质量检测是公路和交通工程研究中的重要内容。
传统的路面质量评估方法通常具有破坏性,如取芯和CBR法,以上方法虽然能有效检测路面质量,但检测效率较低且费时费力,对于多层路面检测结果难以做到准确评估。因此,需要一种简便可靠且无损的检测方法对路面质量进行无损检测。由于瑞利波(SASW)检测法操作简便,无破坏性,同时具有较高准确性的检测结果,目前已广泛应用于工程领域。如:陈云敏等[1]随机选取30处机场跑道混凝土板块并采用表面波对机场跑道路面进行检测,同时进行现场钻芯取样验证路面抗折强度,结果表明:表面波检测可以通过剪切波速度准确判断混凝土强度,且检测结果与取芯法一致。董继业[2]采用瑞利波检测法、室内迭代以及反演路面工况等方式对沥青混合料和沥青路面进行质量检测,分析结果表明:由于路面压实度不足导致沥青路面剥落,同时材料对水损害控制较低。徐晨鸣和周艳红[3]通过瑞利波对高速公路进行检测,并确定了物理检测参数与路基路面质量指标的相关系数,同时构建评价指标,结果表明:瑞利波无损检测结果可靠,受检路面路基质量均达到优秀标准。罗广衡等[4]为探究混凝土表面裂缝深度影响因素,设定不同裂缝深度与频率间的相关实验,探究最优检测频率范围,对比了截止频率法和瑞利波法对裂缝检测的结果。杨成林[5]通过相关实验验证了瞬态瑞利波在浅层地质中检验的可行性。柴华友等[6]通过为频率分离探究了瑞利波反演中的不确定性问题,并以概率统计形式对频散现象进行表征。曲华等[7]为进一步提高了截止频率识别精度,提出了相应的拟合公式验证了截止频率检测的有效性。
目前业内关于瑞利波在路面层系统中传播特性的分析尚少。因此,本文对瑞利波在柔性路面层系统中的传播速度变化、检测频率范围等特性进行研究。
1 研究方法
瑞利波频谱分析(SASW)是利用机械表面波来评估地下材料介质的有效方法。当使用瑞利波从表面穿透介质进行检测时,至少需要穿透一个波长的深度。同时,该方法能够利用不同的波长来评估不同深度的介质。当撞击源发生撞击,可能产生较大范围频率的瑞利面波组合,此时通过记录设备,即动态信号分析仪和高性能计算机,可以在特定时间内记录该频率范围内的相关信息。瑞利波在传播过程中可分为一般模式或高阶模式。
由于不同层刚度的差异可以抑制某些层中的应力波,或者引起一些折射和反射,从而形成不同的射线路径。因此当表面波穿过这个多层系统时,每一层的刚度都会影响表面波的传播,最终导致在相同的频率点产生不同的传播速度。为了识别一般模式或更高模式的波速,研究采用传递矩阵法和动态刚度矩阵法对其速度进行计算。
图1所示为仪器布置及试验安排示意图。通常瑞利波现场分析的典型配置包括两个竖向检波器,并在检波器周边设置一个撞击源,最终通过记录设备对波频进行记录、分析。在整个测量过程中,竖向检波器间距相同,且在路面分层系统中取样需要满足一定的波长范围。
叠加模式是介于叠加与正常模式之间的一种模式(正常模式包括一般模式和高级模式),该模式不具有任何固定形式,其对应模式也被称为视速度或有效速度。其中,表观速度的数值大小取决于撞击源和接收器的实际位置。由于接收器位置位于撞击源附近,使得所测量的波的模式为叠加状态而非分离状态,虽然MASW、f-k法等方法是利用一般模式或高阶模式进行波形测定,但这是由于撞击源的位置远离接收器,才使测量的波具有较好的模式分离,而f-k法在测量过程中需要更多的接收器才能帮助模式分离。这表明以上两种方法的检测过程较为复杂,因此需要分析叠加模式下波的状态来反映实际情况。
2 试验结果与讨论
常见路面层系统具有分散轮廓不规则的特点,其多表现为顶层比底层更坚硬,剪切波速更高等。这一特征与正常分散场地或浅基岩场地的分散剖面相反。具有夹层层状体系的场地与路面层状体系具有一定的相似性。因此,在研究分析路面分层系统时,使用了表1所示的一个特定剖面,以代替实际路面层系统。
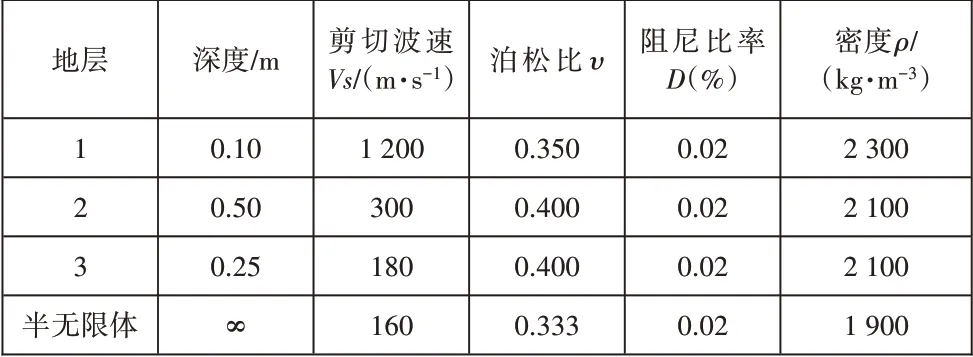
表1 路面层系统土性参数
本研究分别设置两组不同接收器距离,即1号接收器距离D=0.15m和2号接收器距离D=0.30m。由于路面层系统的频率范围相对高于地质位置,因此在保持两个接收器距离不变的同时将频率范围设置在10kHz,设采样间隔为0.000 1s,奈奎斯特频率为5 000Hz,则可满足本文对地下材料剖面测量研究。为了获得更高的分辨率,试验选择了2 048个样本为记录长度,历史记录时间为0.204 7s。时间信号记录如图2(a)和图2(b)所示。
从图2可知,波幅变化信号在0.010s前呈强烈波动变化,而两个接收器在深度分别为S1=0.30m,S2=0.60m,S4=1.2m和S8=2.4m状态下,均表现出幅值随着深度增加而降低。
图3为接收器距离为D=0.15m时,基于瑞利波理论模拟出路面层系统中波的相位谱图,而图4显示了当接收器距离为0.30m时的相位谱图。根据图3可初步判断,当D=0.15m时,其对应波频介于9~11kHz范围内,且该频率范围内存在跳跃次数差异现象。在这种情况下,需假设实际相位周期对应频率为9 000Hz。通过对比图4相可知,图3的循环周期并不完整的,而完整的周期应是由相位角为0开始至相位角为0时结束。因此,当设置接收器距离为D=0.15m时对路面系统进行测量,可能不足以反映出整个分层系统样本的实际状态。由于初步判断不足以描述整体路面系统,初步结果并不能代表最终的结果。因此,试验需要以色散曲线进一步研究分析路面系统,用以验证最初的观察结果。
根据瑞利波检测理论,获取了2种不同接收器间隔的相速度频散曲线。为进一步获取地下材料的刚度剖面,需要进行相关内容的反演计算,其中相速度频散曲线则是分析反演中的重要环节。而在理论相速度计算时则需要使用正演模拟过程进行分析。为保证路面系统中的每一层材料信息的正确性,需要通过分析不同剖面模型以保证最终结果合理可信。通过前人研究可知,在理论频散曲线的计算中,多数研究没有考虑反演过程撞击源和接收器的实际位置。因此为反映实际工况,本研究采用了瑞利波测量期间有关撞击源和接收器的实际位置信息进行反演计算。
图5显示了在瑞利波法计算下的不同模式对应表现行为。其中理论叠加模式,本文采用全局反演计算。将S8之前所有源距离S1的叠加模式绘制在一起,可以看出每个源距离的色散是相似的。在这个图中得到的实验叠加模式并非为现场测量获取,而是基于理论上的叠加模式所形成。由于考虑了撞击源和接收器的实际位置关系,因此可以将理论叠加模式经过反演计算得出实验叠加模式,以模拟出实际状态下瑞利波的传播路径及状态。
(1)观察两个剪切波速图可知,路面层状体系的介质剖面具有波速随深度增大而减小的特征,这与通常的分散介质中完全相反。
(2)路面层系统剖面的表观速度不遵循瑞利波的一般模式,该样本与夹层情况类似。在低于200Hz(或波长大于2m)的频率范围内,叠加模式获得的视速度遵循一般模式的趋势。然而,从200Hz的频率开始,速度稳步增加,直到2 000Hz的频率截止(波长约为0.35m)。观察图5可知,理论叠加模式下的表观速度与实验叠加模式相比具有更陡的梯度,这是由于在获得理论叠加模式的反演过程中没有考虑撞击源和接收器的实际位置导致。
(3)在所有源距离(S1~S8)条件下,较小接收距离(D=0.15m)的剪切波速比较大接收距离(D=0.30m)的剪切波速更加分散。这表明较小的接收器距离的模式计算不太精确。这也说明,较小的接收器距离不适合或不足以用于取样或表征具较大深度和厚度的路面层系统材料。
3 结论
本文通过对瑞利波在柔性路面层系统中的传播速度变化、检测频率范围等特性的研究,得到如下结论:
瑞利波波幅变化通常在0.010s产生波动,且波幅随着检测深度增加而降低。当接收距离为0.15m时,瑞利波会在9~11kHz范围内产生跳跃差异,说明接收器距离较小将影响瑞利波检测的准确性。通过色散曲线分析可知,剪切波速随检测深度增大而减小。在路面系统中,瑞利波表观速度不遵循一般模式下的速度变化。
