基于EV保有量预测的充电站选址规划

于泉，张浩楠，刘芳亮，于加晴，田龙飞，王宇

（1.北方工业大学电气与控制工程学院，北京 100144；2.中交公路规划设计院有限公司，北京 100088）

0 引言

相较于传统燃油汽车，电动汽车（Electric Vehicle，EV）具有环保、绿色、节约能源等优点。我国从2009年开始，通过试点项目、政策激励、财政补贴等手段，已经成为全球电动汽车保有量最大的国家[1]。我国充电设施的数量随之快速增长，但仍满足不了日益增长的充电需求，存在“有车无桩，有桩无车”的现象。充电设施选址如果不合理，不仅影响用户的充电需求，也会造成资源的浪费。因此，科学合理地预测电动汽车增长情况，并以此为基础规划充电设施位置和容量是需要研究的重要问题。

近几年，国内外学者针对充电设施选址定容相关问题做了大量研究。其中，杨洋等人[2]基于截流选址模型构建充电站选址模型，并以用户等待充电时间最小为目标提出了充电站定容模型；赵炳耀等人[3]综合多种约束条件，建立充电站选址定容多目标决策模型，引入层次分析熵权法解决多目标决策难问题；田枫等人[4]考虑用户的充电选择偏好，以最小化充电站建设成本和最大化充电站覆盖构建双目标选址模型，最大限度提高用户的充电便利性；Wang等人[5]模拟驾驶员充电决策过程并利用变分不等式描述电动汽车路径选择和充电行为，以此建立充电站选址定容模型。

目前，对充电站选址的研究大多考虑充电站建设运营成本、用户充电需求等因素，并未考虑随着电动汽车保有量的快速增加，充电设施应如何增设。本文对充电设施的选址定容研究主要针对城市公共充电站，首先采用遗传算法优化的BP神经网络（Back Propagation Neural Network，BPNN）模型预测电动汽车保有量；其次，综合考虑充电站投资方和电动汽车用户双方利益构建电动汽车充电站选址定容模型，提出一种基于Logistic映射的离散二进制粒子群算法（A Binary Particle Swarm Optimization Based on Logistic Chaotic Map，LBPSO）求解；最后，通过案例仿真得到最优充电站位置和容量配置。

1 基于GA-BP神经网络的EV保有量预测

人工神经网络作为人工智能领域的研究热点，是模仿人脑神经元建立的一种数学模型，神经网络至今已经发展出许多模型，其中应用最广泛的BP神经网络因其具有广泛的适应能力、学习能力、多因素非线性映射能力等，常用于各类数据预测。

遗传算法（Genetic Algorithm，GA）由美国John holland教授于1975年在书中首次提出[6]，是一种启发式算法，其原理是仿照自然界生物进化过程，不断地在种群中筛选出优良个体繁衍后代，其算法具有良好的适应性和全局搜索能力，广泛应用在各种工程中。

在进行电动汽车保有量预测时，常用的方法有时间序列预测法、Logistic模型法、Bass模型法等，现有预测方法仅考虑单一因素对电动汽车保有量的影响，并且预测精度不够理想。基于BP神经网络存在的多种优势，本文通过遗传算法优化BP神经网络模型预测电动汽车保有量，其实质是通过遗传算法良好的全局搜索能力优化网络的权值和阈值，从而提高BP神经网络的预测精度和收敛速度。

2 充电站选址定容模型

2.1 模型假设

（1）用户往往选择距离自己最近的充电站充电，并且电动汽车剩余电量能满足用户至少到达一个充电站进行充电；

（2）用户行驶费用与行驶距离、电量消耗成正比；

（3）充电站有足够的停车位供电动汽车等待充电，电动汽车按照到达顺序排队充电。

2.2 目标函数

从充电站这一公共服务设施建设角度出发，其建设位置必须为路网中产生充电需求的用户提供满意的服务，在保证用户需求的基础上，本文以最小化综合总成本为目标，以区域充电需求为约束，考虑充电站内快慢充电桩数量，构建充电站选址定容模型。引入0-1变量xj，xj=1表示在充电候选点j建站，xj=0表示不在充电候选点j建站。

式（1）～式（9）中：Fcost为综合总成本；Bj为充电站j年均建设成本；Aj为充电站j年均运营成本；U为用户年充电成本；j为充电站候选点；r0为投资回收率；m为充电站运营年限；Lj为充电候选点j的单位面积土地价格；Sj为充电候选点j的占地面积；Cfj为充电候选点j的快充充电桩数量；Sf为快充充电桩单价；Csj为充电候选点j的慢充充电桩数量；SS为慢充充电桩单价；Fj为充电站j固定成本；Q为区域内平均每天的充电需求；E为电动汽车保有量；γ为电动汽车中每天需要充电的电动汽车比例；P为电动汽车额定电池容量；Wf为快充充电桩功率；Ws为慢充充电桩功率；t为每台充电机平均每天工作时间；η为充电机充电效率；pc为电网每度电单价；Qi为充电需求点i的充电需求；δi为充电需求点i的权重；dij为充电需求点i到充电候选点j最短距离；pd为电动汽车每千米行驶花费；i为充电需求点；Fmax为可投入最大成本。

式（1）为综合总成本最小公式；式（2）计算充电站j折算至每年的年均建设成本；式（4）计算充电站j的运营成本，由电站电量消耗成本构成；式（6）计算用户到充电站候选点j的年充电成本，由用户到充电站的行驶费用构成；式（7）计算充电需求约束，充电站供给大于等于该区域总充电需求；式（8）计算区域电量总需求约束；式（9）为投资花费小于最大预算成本。

2.3 改进离散二进制粒子群算法

电动汽车充电站选址定容问题是多变量、多约束的非线性整数规划问题，采用传统的方法往往无法解决，因此本文采用离散二进制粒子群算法求解，该算法由美国Kenndy和Eberhart教授提出，可以解决本文提出的离散问题[7-8]，是一种群体智能优化算法，具有调节参数少、收敛速度快、求解质量高等优点。基本粒子群算法的粒子速度和位置更新公式为：

式（10）中：V为速度；X为位置；k为当前迭代次数；w为惯性权重；d为搜索空间的维度，d=1,2,...,D；i为粒子编号，i=1,2,...,n；c1和c2为加速因子；r1和r2为分布在[ 0,1]区间的随机数，P为个体极值；Pg为群体极值。

离散二进制粒子群算法是在基本粒子群算法基础上改变粒子位置更新公式而得到的，采用Sigmoid函数将粒子速度取值映射到区间[ 0,1]上，然后粒子通过式（11）改变位置：

混沌是确定性系统自发产生的不稳定现象，一个系统如果在其进化的过程中对初始的状态非常敏感，则这个系统就是混沌系统。该系统具有随机性、遍历性、不确定性等。主要的混沌映射有Logistic映射、Tent映射等。由于混沌系统的遍历性，使其可以不重复地搜索范围内的所有状态，又由于Logistic映射结构简单，如式（12）所示，且具有良好的安全性，因此利用Logistic映射来优化BPSO的初始种群位置并在迭代过程中随机扰动粒子位置，从而提高算法的遍历性。

式（12）中：k=1,2,...,n；3.57＜μ≤4，为分支参数，本文μ取4。

3 案例分析

本文选取某市某一区域为例，该区域总面积为25.2km2，共有8条道路。拟规划若干数量的充电站，以满足该区域电动汽车用户的充电需求，并尽量使综合总成本最小。根据道路交通流量、电网约束、交通便利性做出合理假设，共选定了8个充电需求点和16个充电站候选点，见图1所示。

电动汽车充电站运营年限设为20年，投资回收率为0.25，快充桩2.5万元每台充电功率60kW，慢充桩0.16万元每台充电功率7kW，平均每台充电桩运作20h，工作效率为0.9；每天需充电的电动汽车比例为0.2，电动汽车型号统一，额定电池容量为30kW·h，每行驶1km花费1元，电网每度电0.5元。根据北京市出台的标准文件《电动汽车电能供给与保障技术规范：充电站》[9]，设定备选充电站的基本参数见表1，各类型土地成本分别为商业用地1.524 6万元/m2、居民用地2.672 7万元/m2、工业用地0.915 1万元/m2。

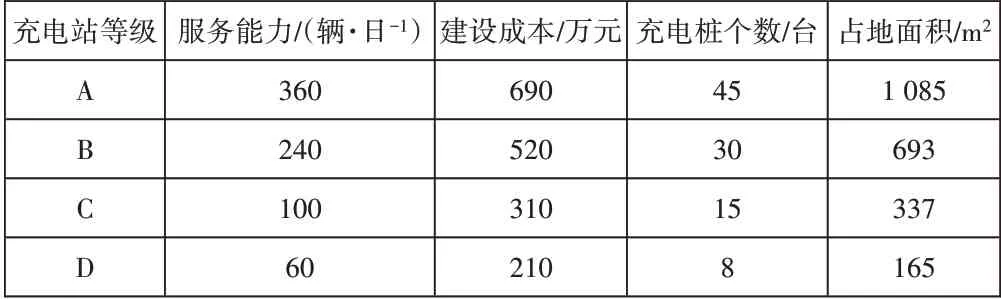
表1 充电站等级及对应的建站参数

基于该区域历史数据训练的GA-BP神经网络对电动汽车保有量预测的结果为：2025年0.27万辆、2030年0.78万辆、2035年1.05万辆、2040年2.32万辆。

假设充电桩的平均功率是34kW，将2030年作为目标年，则该区域每天的充电需求为46 800kW·h，平均分配到各个需求点，需要77台充电桩。当充电站按等级A配置时，需要至少2座，当充电站按等级D配置时，需要10座，因此到目标年，该区域最少需要2座、最多需要10座充电站。通过道路拓扑图求得各个需求点到候选点的最短路，设定快慢充电桩比例为1∶2，统计每条道路电动汽车占比，得到每个需求点权重分别为0.15、0.2、0.05、0.125、0.025、0.1、0.155、0.195。LBPSO算法参数设置为：种群规模为25，最大迭代次数为150代，粒子的个体和社会学习因子均为2，惯性权重为0.4，采用MATLAB2018b软件编程求解，在所有取值中，最少成本对应的规划方案即为最优方案。

建设不同数量的充电站综合总成本如图2所示，从计算结果可以看出：充电站数量建设过少，则会造成用户充电成本上升，充电站数量过多则会造成充电站建设运营成本增加，当建站数量为7时，综合总成本最低为633.9万元。

采用LBPSO算法分别求解该区域2025年、2030年、2035年和2040年的充电站规划方案如表2所示。

表2 预测年份充电站规划方案

从表2可以看出，随着电动汽车保有量的不断增长，需要不断增加费用扩建充电设施，若不规划新的充电站候选点位，则在原有电站选址基础上增加充电桩数量来满足需求是最优策略；当充电桩数量超过电站最大容量时，则不得不在其他候选点位建设充电站；进一步可以发现，选址位置的轻微变化说明模型的综合总成本中，用户年充电成本，即用户因车辆电量不足而去电站充电这个过程所耗费用是相当巨大的。

4 结语

电动汽车充电站的规划对电动汽车发展十分重要。本文考虑多方面因素，建立充电站建设运营和用户费用综合总成本最小为目标的规划模型；提出的LBPSO算法是在BPSO算法基础上，引入混沌映射干扰粒子位置，使其在充电站选址定容中具有更强的搜索和寻优能力；随着电动汽车保有量的增加，在原有站点基础上增加充电桩是最优扩建措施，且在电站规划中，用户年充电损失成本占比较大。