基本入手 化繁为简
——基本量法的解题程序
2022-11-22俞海东李柏翰
俞海东, 李柏翰
(1.嵊州中学,浙江 嵊州 312400;2.浙江师范大学教师教育学院,浙江 金华 321004)
数学思想方法是数学在漫长发展过程中所积累的文化灵魂,将数学思想方法渗透到课堂教学有助于学生数学学习能力的发展、锻炼数学思维,是落实学科核心素养的重要途径.笔者在实践教学中发现:当学生碰到陌生复杂的问题时,在如何审题以及如何解题方面存在一定的困难.基于此,笔者以渗透数学思想方法为导向,以基本量法为核心方法,根据波利亚解题理论和卢正勇教授的解题程序,形成基本量法的解题程序.本文以平面向量问题、解三角形问题、函数与方程问题为例,将解题过程一般化、可操作化,让学生学会对问题的条件和结论进行适当分解和组合,建立已知条件和目标之间的联系,使学生在解题过程中体会思维分拆的过程,形成明确的解题思维程序.
1 基本量法的概念及解题程序
17世纪初,韦达提出用几个字母来表达未知量或已知量的想法.在数学问题解决的过程中,往往需要根据题目所给的条件设定未知量,并分析已知量和未知量之间的关系,选择其中的一些量,使得其余量可以用它们表示,这些量被称为基本量.举例而言,平面直角坐标系中任意一个向量都可以由两个向量(1,0)和(0,1)线性表示,因此这两个向量(1,0)和(0,1)称为基本量.化繁为简是处理数学问题的常见方法,将题目中的量用基本量来表示体现的正是这种化繁为简的思想.以基本量为主线,来解决数学问题的方法称为基本量法.
根据波利亚解题理论和卢正勇教授的解题程序,本研究认为基本量法的解题程序包括:审题、分析、解答、验证反思这4个环节.认真审题的核心是寻找合适的变量表达已知量和未知量;分析环节是寻找合适的基本量表达数学问题;解答环节的关键是寻找合适的等式并利用其消元,以达到简化问题、解决问题的目的;验证反思环节是总结选择基本量的经验,让学生学会举一反三.
2 基本量法的解题实践
2.1 平面向量问题中的基本量法
例1已知平面向量a,b满足|2a-b|=2,且a·(a+b)=1,求|a+b|的取值范围.
研究思路基底是平面向量中的重要概念,在涉及多个向量的问题中,选两个作为基底,将条件和目标的向量都用基底表达,再将问题转化为两个基底的模长和数量积的方程组问题.对于问题的解决能起到化繁为简的效果.
解题程序1)审题:该问题包含向量的运算、向量的模等要素,a,b可以通过向量的加法和减法运算、向量的数量积转变为题中的已知条件和目标.通过基本量法将问题转化为两个基底的模长和数量积的方程组问题.
2)分析:本问题可以选择a,b作为基本量.由题意知
4a2-4ab+b2=4,
a2+ab=1,
设|a|=x,|b|=y,a·b=xycos
8x2+y2=8,
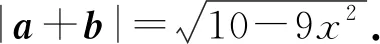
3)解答:再考虑-|a|·|b|≤a·b≤|a|·|b|,即
-xy≤1-x2≤xy,
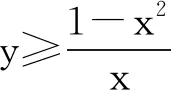
代入目标函数,得
1≤|a+b|≤3.
4)验证反思:在平面向量问题中,可以选择基底作为基本量,对题目中的条件进行化简.同时也需要注意向量问题中的“隐性”条件:
-|a|·|b|≤a·b≤|a|·|b|.
2.2 解三角形问题中的基本量法
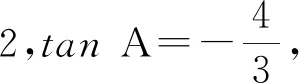

图1
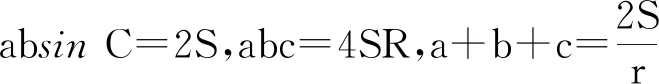
解题程序1)审题:该题干中的信息包括内切圆半径r、角A、所求变量为面积S,可以将内切圆半径r和面积S用三角形的基本要素3个角和3条边来表示.在△ABC中,基本量是角A,B,C和边a,b,c.

3)解答:本题中角A为已知量,目标函数中需要求bc的最小值,因此需要根据上述已知条件消去a.条件③可以因式分解为
与条件②联立,可得
b+c-a=2,
将其代入条件③,化简得

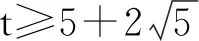
从而
于是
4)验证反思:三角形的3条边与3个角是三角形的基本要素,因此在解决三角形问题时,把三角形的3条边与3个角作为基本量是解决问题的突破口.
2.3 函数与方程问题中的基本量法
例3已知函数f(x)=ax2+bx+1(其中x>0,a>0,b∈R),设方程f(x)=x有两个实数根x1,x2.试解决以下问题:
1)如果x1<2
2)如果0 研究思路一元二次方程的根与系数存在关系,一元二次方程的系数可以用根来表示,同样地,根也可以用系数来表示.把根作为基本量去表示系数,或把系数作为基本量去表示根能起到精简题干、化繁为简的作用.这为也我们解决函数与方程问题提供了思路. 解题程序1)审题:该题关于x1,x2的信息最多,可以选择x1,x2作为基本量,把系数a,b以及对称轴用x1,x2表示. 2)分析:根据韦达定理,可得 进而得到 至此已将题中的其他量用x1,x2来表示. 3)解答: ①由0 -3<(x1-1)(x2-1)<3. 进而得到x0>-1. ②条件中的等式有 若x1-x2=2,则x2<0,与a>0矛盾.利用等式消元,得 得 故 4)验证反思:在二次函数与方程的问题中,根与系数都可以作为基本量.把题干中的量用基本量表示,既建立了量与量之间的联系,又起到消元的作用.研究的目标从多个变量转为少数几个变量,体现了数学的简洁美. 基本量法基于消元、转化等数学思想,从数学思想方法的角度对问题解决提供理论指导.本研究以平面向量问题、三角形问题、函数与方程问题为例,分析了3个例题的基本量选取以及基本量法的解题程序.将基本量法的解题程序运用于教学实践,能让学生体味数学思想方法的魅力,促进学生学习能力以及思维能力的发展.对于基本量法的解题教学,教师应该特别关注以下3个方面. 第一,重视基本量法解题程序的4个环节.教师需要深度理解基本量法的解题程序,落实审题、分析、解答、验证反思这4个环节.审题的核心是寻找题目中量与量的关系,选择合适的量作为基本量;分析环节则需要在“审题”的基础上,把题目中的所有量都用基本量表示,达到统一变量的目的;解答环节的关键是寻找合适的等式并利用其消元,以达到简化问题、解决问题的目的;验证反思环节,教师需要总结选基本量的经验,使学生在后续的解题中学会举一反三. 第二,注重归纳总结各类问题中的基本量.高中数学课程内容突出函数、几何与代数、概率与统计、数学建模活动与数学探究活动这4条主线.对于不同的知识点,教师需要根据知识的生成脉络,总结解题所需的基本量.举例而言,△ABC的3条边a,b,c可以作为解三角形问题中的基本量,3个角A,B,C、面积S、外接圆半径R和内切圆半径r都可以用3条边a,b,c表示.在等差数列中,可以选择首项a、公差d和项数n作为基本量;在等比数列中可以选择首项a、公比q和项数n作为基本量.平面向量问题中可以选择两个不共线的向量作为基本量.只要我们明确了事物的基本量,那么事物的本质就平铺在台面上,一切问题就能迎刃而解.在解决各类问题时,我们可以根据问题的类型与解题目标,选取适当的基本量,通过基本量的确定来迅速完成解题任务. 第三,设计有效的题组训练.数学思维水平的提高离不开一定的训练量,教师在课堂中设置有效的题组训练是非常必要的.尤其是同一类问题,教师需要设置一题多变、一题多解的题组,引导学生思考“该如何选择基本量”“基本量的选择是否唯一”等问题.举例而言,在解三角形问题中,3条边a,b,c可以作为解三角形问题的基本量,两边及其夹角a,b,C也可以作为解三角形问题的基本量.教师需要设置有效的题组训练,让学生知道在解题时选择哪些量作为基本量是最恰当的.通过设置有效的题组训练培养学生思维的发散性,让学生洞悉基本量法的本质.

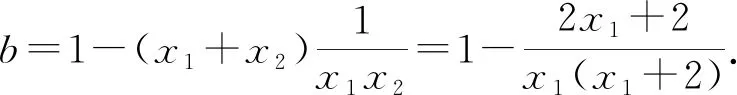

3 启示
