聚焦学科素养 凸显“三性”教学 指向深度学习——有感于浙江省2021年中小学正高级评审之“弧度制”说课环节

冯 斌, 刘次律

(1.宁波市教育局教研室，浙江 宁波 315000；2.梦麟中学，浙江 余姚 315400)

“说课”是促进教师专业水平提升的重要途径，被广泛用于各级评优活动、教师职称评审环节.“弧度制”是高中数学公认的“难教、难学”的内容之一.本文根据浙江省2021年中小学正高级评审之说课环节的“弧度制”说课内容，在新课程、新教材“双新”背景下，结合平时的教学调研基础上加以提炼的成果.在此谈谈笔者的体会与感悟，以抛砖引玉.

1 对“说课”的认识

“说课”顾名思义，对象是“课”，方式是“说”，是在备课的基础上，面对同行或专家领导，在规定的时间内，针对具体课题，根据课程标准、教学理论、学生学情等，采用讲述为主的方式，阐述自己的教学设计及理论依据.“说课”不仅要说清“为什么学”“学什么”“怎么学”,还要说清“为什么这么学”“学得怎样”.说课的基本内容有：说教材内容、说学习目标、说学情、说学法、说教学过程、说目标检测、说教学反思等，其中“说教学过程”是务实部分，其他为务虚部分，务虚与务实的时间一般按“三七”或“二八”分配.

2 对“弧度制”一课的教学思考

2.1 “弧度制”一课的育人价值

本节课是人教A版新教材普通高中教科书《数学(必修1)》第五章中“任意角与弧度制”的第二课时，内容包括：“1弧度”的定义、弧度与角度的互化、弧度制下的弧长公式与扇形面积公式.《普通高中数学课程标准(2017年版2020年修订)》对此内容的要求是：了解弧度制，能进行弧度与角度的互化，体会引入弧度制的必要性[1].本节课的重点是：弧度制含义的理解、弧度与角度的互化.弧度制不仅丰富了角的度量方法，还是学习三角函数的预备知识，也为高等数学微积分的研究奠定了基础.弧度制的本质是用线段长度度量角的大小，弧度制下角的集合与实数集合建立了一一对应关系，为数学研究带来优越性和更广泛的应用性.本节课蕴涵着丰富的数学教学方法，如类比、特殊到一般、数形结合等，是提升学生数学抽象、数学运算、逻辑推理素养的良好载体.

2.2 “弧度制”一课的教学问题诊断分析

学生对本节课的认知基础主要有：

1)关于度量制度，学生在初中阶段学过两类，即十进制和六十进制，积累了如度量长度、质量的经验，初步认识到不同的度量制度能给解决问题带来方便.

2)对角的度量，学生在初中阶段学习了角度制、角度制下的弧长公式和扇形面积公式，对学习的路径、方法具有初步的体验.

3)上节课学习了任意角的概念，知道角有正角、负角和零度角，为弧度制下角的集合与实数集合建立一一对应关系奠定了基础.

学生戏称“弧度制”为“糊涂制”，究其原因：一是学习弧度制的目的不清楚；二是定义“1弧度角”的原因不明了.为此，让学生经历“弧度制”概念的形成过程，体会研究过程所蕴涵的类比、特殊到一般、数形结合等思想方法.

2.3 “弧度制”说课的重点与难点

说课如同上课一样是有重点的.笔者认为“弧度制”一课是一节典型的概念课，本节课的说课重点是：说清楚弧度制建构的“三性”，即必要性、合理性、优越性.

2)合理性：弧度制的理论基础是弧长与半径比值的不变性.在同一量的不同度量方式中，需要满足一一对应、同增同减的基本关系，一般情况下需要满足正比例关系或线性关系.教学时在学生“最近发展区”设计适合学生思维水平的数学问题链，使得知识的形成自然而合理.

3)优越性：在中学阶段，建立弧度制的优越性主要体现在两个方面：一是统一进制，“角度制”的度、分、秒里的数并用了十进制与六十进制，“弧度制”下统一用十进制，给数学研究带来方便；二是简化公式，弧度制下弧长与扇形面积公式非常简洁，这符合数学追求简洁美的需求.

本节说课的难点是弧度制的建构，主要内容包括：弧度制的度量单位是什么？弧度制的本质是什么？弧度制的进位制是什么？角度与弧度有何换算关系？突破难点的主要教学策略是：类比学生已有的认知基础“角度制”来建构，以“问题引领学习”，通过学生自主学习、合作交流的方式逐步推进，并结合多媒体辅助教学.

3 “弧度制”一课的说课片段分享

本轮课改是以学科核心素养为导向的，数学教学的终极目标是“三会”.笔者的教学主张是“学习即研究，教学即研究指导”，以研究一个数学对象的基本套路为依据，以问题引领学习，通过主干问题驱动，用问题分解学习目标，在问题研究与解决的过程中达成学习目标.本节是典型的概念学习课，学习方式按概念的形成来进行，教学过程包括：背景—概念—表示—深化—应用.以下就“说教学过程”环节中的“弧度制的引入”“弧度制概念的建构”“角度制与弧度制的换算”这3个部分的说课与同行们分享.

3.1 弧度制的引入——说“必要性”

度量是人类生产生活、科学研究不可缺少的内容，要进行度量必须要确定度量单位.由于不同的需要，同一个量可能有多个度量单位，如度量长度可以用米、英尺、码等不同的单位制，度量质量可以用千克、磅等不同的单位制.不同的单位制能给解决问题带来方便.对角的度量，初中阶段已经学过“角度制”及“角度制”下的度、分、秒里的数并用了十进制与六十进制，角度制会对研究带来很多不便(如60°+1=？)，自然要问：能否像度量长度那样，用十进制的实数来度量角的大小呢？

设计意图学生在初中阶段已学过角度制，习惯了用角度制度量角的大小，“引言”制造学生认知上的冲突，激发学习兴趣，体现了弧度制学习的必要性.美国著名教育心理学家奥苏柏尔曾说过：“要我将教育心理学的规律总结为只有一条就是：‘要知道学生已经知道了什么，探究它，并据此进行教学’.”[2]笔者认为这也是教学的一条基本原则.

3.2 弧度制概念的建构——说“合理性”

弧度制概念的建构是本节说课的重点也是学生学习的难点.通过教师设计“问题串”与追问，以问题引领学习，通过主干问题驱动，通过学生自主学习、合作交流的方式逐步推进，结合多媒体辅助教学，突出重点，突破难点.

情境1如图1，自行车的大齿轮与小齿轮通过链条相连，当链条移动一定的长度时，大齿轮转过的角度比小齿轮转过的角度小.为什么？

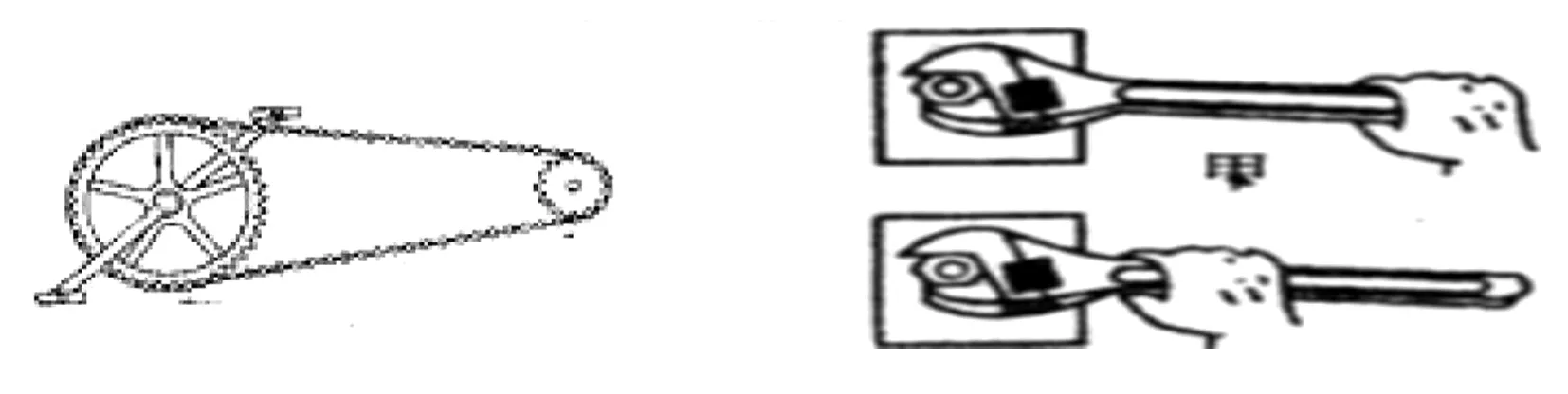
图1 图2

情境2如图2，用直扳手扳动螺母时，螺母转过相同的角度，扳手臂上手握点越近则转过的弧长越小；手握点越远则转过的弧长越长.为什么？

设计意图弧度制的建构需要经历一个过程，不能急于求成.从学生身边的实例出发，激发学生的好奇心与学习兴趣，引导学生用数学的眼光观察现实生活中的现象，分析现象背后的数学本质，学会用数学的思维思考问题.同时激活旧知，联想初中建立的圆心角与圆心角所对的弧长、半径这三者的制约关系，为弧度制的建立奠定基础.

问题1利用几何画板作出多个同心圆，并设定一个固定大小的圆心角α，对每个画出的圆度量出角α所对的弧长与半径，得到一组组数对(li，ri)，并将这些数对放在直角坐标系中，观察有怎样的关系？

追问1初中角度制的研究经历了“定义单位角—命名单位角—用单位角度量其他角”的过程，类比角度制的研究，我们如何合理定义十进制下的单位角？如何给它命名？如何用单位角度量其他角？

师生活动教师给出问题后，借助多媒体辅助教学，先让学生独立思考，再小组交流，然后让学生阅读教材：“1弧度”的规定、记号、表示、读法，弧度数的绝对值公式，特别地，当r=1时，可以直接用弧长度量角.

追问2依照以前概念研究的套路，接下来我们应该进行怎样的研究？

设计意图让学生通过从定性到定量、特殊到一般，经历“1弧度角”概念的形成过程，体会定义的合理性.追问1、追问2的设计是对数学学习活动与经验的再梳理，明确研究的路径，局部范围内渗透单元学习的理念，凸显系统思维视角，帮助学生养成良好的数学学习习惯，促进学生深度学习[3]，从而进一步提升学生的数学抽象、逻辑推理核心素养.

3.3 角度制与弧度制的换算——说“优越性”

关于单位换算，学生在义务教育阶段学过同一度量制下两种单位的换算，例如米、厘米、毫米的换算，度、分、秒的换算等；也学过两种不同度量制的换算，如公顷与平方米的换算等.角度制与弧度制是角的两种度量制，它们也必有内在联系，发现这种内在联系是数学研究的一个基本任务.为此，通过设计以下3个问题引导学生探究换算公式及简单应用，并从中体会引进弧度制的优越性.

问题3学习了角的度量的两种制度，请同学们对弧度制与角度制做个比较.

师生活动通过生生、师生互动，从两种制度的“名称、单位、进制、本质”等维度形成共识，进一步深化对“弧度制”的认识，使学生对“弧度制”不再“糊涂”.

问题4弧度制、角度制都是角的度量制，它们之间应该可以换算，如何换算？填写特殊角的度数与弧度数的对应表(如表1所示)：

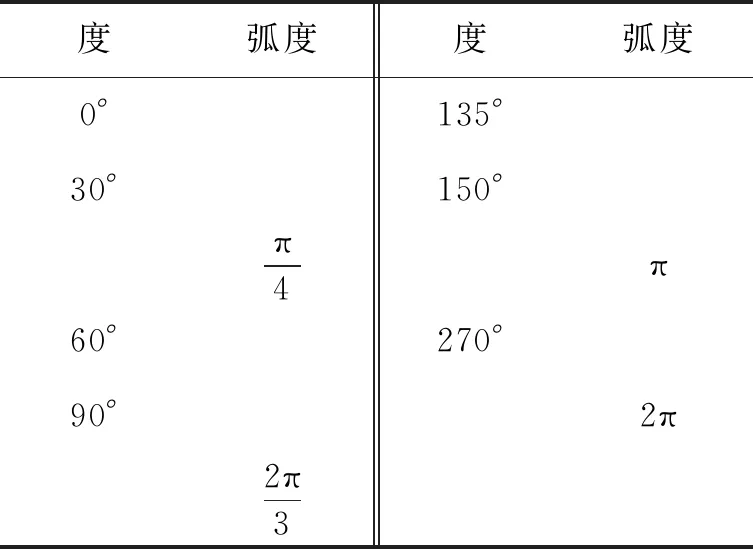
表1 特殊角的度数与弧度数

问题5利用弧度制证明下列关于扇形的公式：

其中R是圆的半径，α(其中0<α<2π)为圆心角，l是扇形的弧长，S是扇形的面积.

设计意图体会弧度制下角的集合与实数集R建立的一一对应关系，体会弧度制下弧长、扇形的面积公式的简洁性，建立弧度制的优越性，从而进一步提升学生的数学运算核心素养.

4 结束语

“双新”背景下的关键词是学科核心素养，“说课”的内容必然围绕核心素养组织和展开，并最终指向学生核心素养的生成和发展，如“说教材内容”应站在单元教学视角揭示内容本质、研究方法、育人价值；“说学习目标”应围绕“四基、四能、核心素养”展开；“说教学过程”应以“研究一个数学对象的基本套路”为指导设计说课内容.以上弧度制概念建构的说课环节体现“必要性、合理性、优越性”，笔者认为一般数学概念教学的说课都应该以这3个属性为主线展开，充分体现概念的形成过程、思维的层次性与深刻性.