基于组合近似模型桁架检测装置稳健性优化
2022-11-21赵清海陈建良
朱 浩 赵清海 张 亮 陈建良 徐 冲
(青岛大学a.机电工程学院;b.电动汽车智能化动力集成技术国家地方联合工程研究中心,山东 青岛 266071)
作为支撑载体,桁架结构因材料的稳健性,在桥梁、建筑、运输和航天器结构中均具有广泛的应用[1-3]。桁架结构性能的优化设计在工程领域仍具有重要研究意义,但仅追求轻量化而忽视桁架的稳健性,会使桁架产生性能波动和结构失效问题。目前,桁架优化主要集中在算法优化方面,W.C.DORN[4]引入数值方法实现了桁架结构的拓扑优化,解决了使用解析法求解Michell桁架[5]较难实现的问题;G.I.N.ROZVANY 等人[6]提出的优化布局理论,可以实现桁架结构尺寸、形状及拓扑的综合优化。近年来,随着计算数学的大力发展,以启发式算法为代表的现代优化算法在桁架优化设计中也得到了推广应用。S.O.DEGERTEKIN 等人[7]提出了Jaya 算法,解决了桁架结构尺寸、布局、规模等优化问题。此后,粒子群算法[8-9]、狼群算法[10--12]、花授粉算法[13-14]等智能算法在结构优化中的应用越来越广泛。B.GEBRAIL等人[15]利用花授粉算法,对二维和三维桁架结构进行尺寸优化,将局部搜索和全局搜索有效地结合;龚雨兵[16]利用改进路径信息素的蚁群算法,对多杆平面桁架及空间桁架进行分析与优化,优化效果较传统智能算法有所提高;LI Y C等人[17]采用改进粒子流算法,实现了桁架形状与尺寸的优化。以上研究虽在算法上改进了桁架优化率,但没有考虑外界不确定因素造成的可靠性问题。因此,桁架优化开始考虑不确定优化设计。于利磊等人[18]考虑约束函数及目标函数的鲁棒性,将工程结构稳健优化问题转化成双目标稳健优化问题;李小刚等人[19]构建了Kriging近似模型的稳健优化设计方法,实现机械结构优化设计;M.CARRASCO 等人[20]提出了数学规划解决方差-期望模型,找到稳健结构。上述研究考虑了优化中的稳健性问题,但在数学模型精确度上存在优化空间。虽然桁架结构优化设计在算法上已取得了一定进展,但在工程运用中,桁架结构优化会因不确定因素产生稳健性问题。因此,针对桁架自动检测装置,本文采用组合近似模型,对某桁架检测装置可靠稳健性进行优化设计,该设计有效提高了桁架结构的可靠性与稳健性,满足桁架结构轻量化和的设计要求。
1 桁架结构及设计参数
桁架自动检测装置三维模型如图1所示。桁架自动检测装置由4根立柱、2根纵梁、1根横梁和检测机械臂组成。该装置处于工作状态时,横梁在2根纵梁上左右移动,检测机械臂在横梁上可前后移动,桁架自动检测装置的工作范围可覆盖其所处的三维空间。
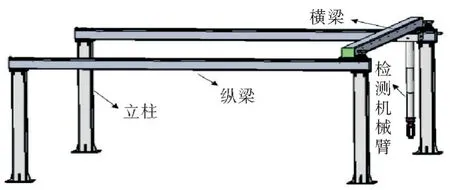
图1 桁架自动检测装置三维模型
对桁架检测装置模型结构材料参数进行设置,模型结构材料参数进行设置如表1所示。

表1 模型结构材料参数设置
检测机械臂的材质为铝合金,密度较小,本身质量较小,其尺寸优化对检测装置整体质量影响较小,因此选择桁架立柱、横梁和纵梁截面形状尺寸作为设计变量进行优化设计。桁架自动检测装置设计变量如图2所示,图2中,L1为横梁截面单元长度;h1为横梁截面单元侧壁厚;h2为横梁截面单元主壁厚;L2为纵梁截面单元长度;h3为纵梁截面单元侧壁厚;h4为纵梁截面单元主壁厚;L3为立柱截面单元长度;h5为立柱截面单元侧壁厚;h6为立柱截面单元主壁厚。
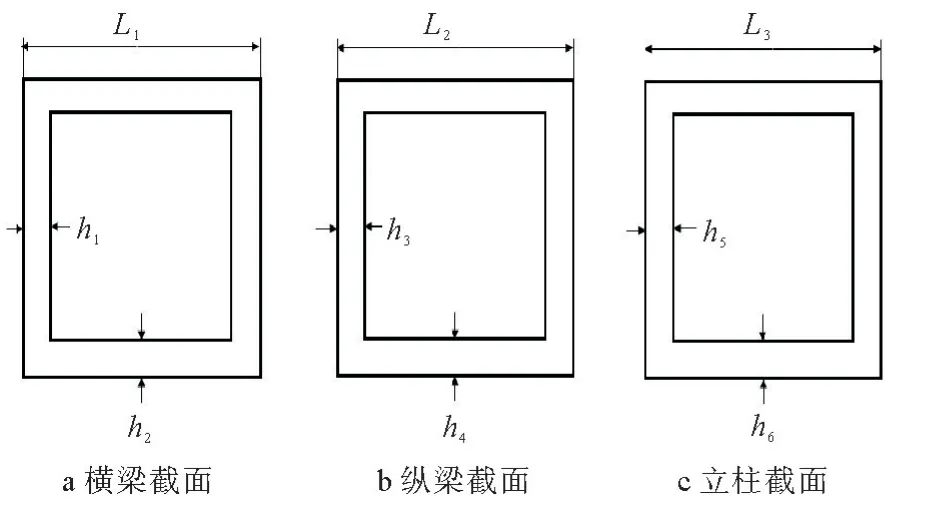
图2 桁架自动检测装置设计变量
通过分析设计变量对目标函数的影响程度,获取设计变量的灵敏程度,更好地把握设计变量的取值和优化范围,设计变量对桁架质量的影响如图3所示。由图3可以看出,在满足约束条件下,h1~h6对桁架质量影响较大,而L1~L3对质量的影响程度低很多。
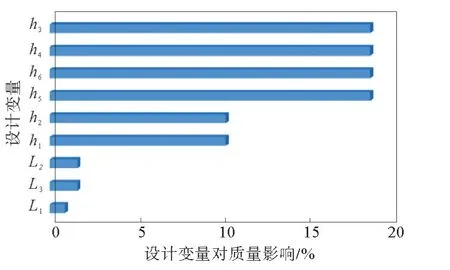
图3 设计变量对桁架质量的影响
考虑设计变量对目标函数的影响程度和实际要求,对桁架检测装置优化变量参数及取值范围进行设置,优化设计参数初始值如表2所示,优化设计参数取值范围如表3所示。

表2 优化设计参数初始值

表3 优化设计参数取值范围
2 桁架结构确定性优化设计
2.1 约束条件确定
横梁的应力为弯曲应力,其应力与应变是由横梁自重和检测机械臂重力共同作用产生,横梁最大应力与应变的发生位置在横梁中点处,横梁应力与应变分别为

式中,σ1为横梁受到的最大弯曲应力;M1为横梁最大弯矩;W1为横梁抗弯截面系数;ρ为横梁密度;Lh为横梁长度;ms为检测机械臂质量;ε1为横梁最大变形;E为桁架材料的弹性模量;I1为横梁的截面惯性矩。
纵梁应力也为弯曲应力,由自重、横梁和检测机械臂重力共同作用产生,纵梁的最大应力与应变发生位置为纵梁中点处,纵梁应力与应变分别为

式中,σ2为纵梁受到的最大弯曲应力;M2为纵梁最大弯矩;W2为纵梁抗弯截面系数;Lz为纵梁长度;ε2为纵梁的最大变形;I2为横梁的截面惯性矩。
立柱的应力为压应力,其应力与应变是由横梁、纵梁与检测机械臂重力共同作用产生,立柱应力与应变分别为

式中,σ3为横梁受到的最大弯曲应力;ε1为横梁的最大变形。
对上述约束条件进行设置,约束条件及约束值如表4所示。

表4 约束条件及约束值
2.2 确定性优化模型
桁架检测装置确定性优化设计数学模型为

式中,X为设计变量集;σs为最大拉压应力;εs为最大应变值。
2.3 优化结果与分析
对建立的确定性优化模型进行求解,获取其目标函数值随迭代次数求解变化情况,桁架总质量随迭代次数变化曲线如图4所示。图4中,红色为不满足约束的解,黑色为可行解,绿色为最优解。由图4可以看出,当迭代次数为185次时,目标函数取得最优解,即在满足约束条件下,桁架总质量取得最小值,为313.06 kg。横梁截面单元尺寸Pareto图如图5所示,纵梁截面单元尺寸Pareto图如图6所示,立柱截面单元尺寸Pareto图如图7所示。

图4 桁架总质量随迭代次数变化

图5 横梁截面单元尺寸Pareto图

图6 纵梁截面单元尺寸Pareto图
图5~图7中的红色部分为不满足约束的解,黑色部分为可行解,绿色部分为最优解。由图5可以看出,横梁截面单元长度高于0.141 m,且主壁厚不低于0.003 23 m 时,绝大部分满足约束条件,绿色点为满足约束的最佳设计尺寸;由图6可以看出,纵梁截面单元长度低于0.138 5 m 时,采样点全部不满足约束条件,纵梁截面单元长度高于0.138 5 m 时,且侧壁厚不低于0.003 66 m,主壁厚不低于0.004 735 m 时,采样点绝大部分满足约束条件,绿色点为满足约束的最佳设计尺寸;由图7可以看出,立柱截面单元长度高于0.138 m时,且侧壁厚不低于0.002 94 m,采样点绝大部分满足约束条件,绿色点为满足约束的最佳设计尺寸。

图7 立柱截面单元尺寸Pareto图
3 桁架可靠稳健性优化
3.1 6σ 稳健性数学优化模型
稳健性优化是在确定约束条件与目标函数的前提下,寻找优化中波动较小的区域。其目的主要防止未曾考虑的因素对优化结果的影响,提高优化的可靠度。优化模型为

式中,X优化变量集;F(X)为目标函数;H(X)为约束条件;XL为优化变量下限;XU为优化变量的上限;n表示σ水平。
3.2 桁架稳健性优化分析
采用响应面模型与径向基神经网络模型的组合近似模型,对其可靠稳健性进行优化分析。组合近似模型权重系数及组合近似模型为

式中,MEN为组合近似模型的响应预测值;ωi和Si分别为第i个模型的权系数和响应预测值,权系数之和等于1;Ei为第i个单一近似模型的均方根误差;ˉE为所有单一近似模型的平均均方根误差;ω*i为近似模型第i个控制权重系数;N为近似模型个数,N=2;α和β为近似模型控制参数,当α=0.05,β=-1时,组合近似模型精度较高。
通过实验设计采样,生成响应面模型与RBF模型的置信水平R2,响应面模型R2值如图8所示,RBF模型R2值如图9所示。由图8和图9可以看出,当响应面模型R2=1,RBF模型R2=0.998 25时,一般认为R2>0.9,则认为近似模型具有高可信度。
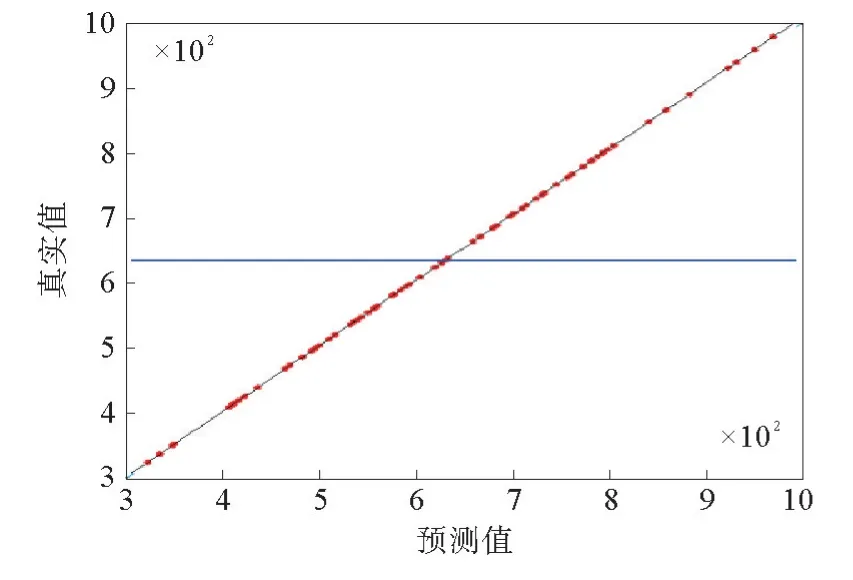
图8 响应面模型R2 值
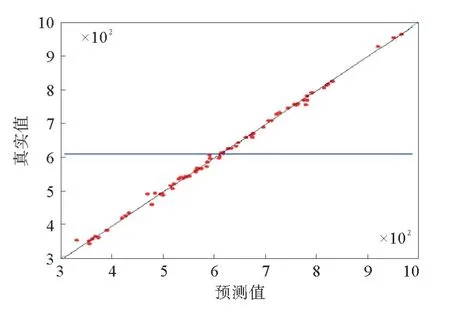
图9 RBF模型R2 值
经计算可知,组合模型表达式为

采用6σ分析中的均值一阶可靠性分析,并定义9个初始设计变量为随机变量,变异系数为0.01,对桁架自动检测装置的6个输出响应进行质量水平检查与可靠性分析,输出响应可靠度分析结果如表5所示。

表5 输出响应可靠度分析结果
由表5可以看出,桁架自动检测装置输出响应的横梁应变、纵梁应变、立柱应变和立柱应力的质量水平都达到了8σ,可靠度为1,不需要稳健性优化。而对于桁架自动检测装置输出响应中的横梁应力和纵梁应力质量水平达不到6σ的情况,可靠度不为1。其中,横梁应力的质量水平为0.362σ,可靠度为0.283;纵梁应力的质量水平为0,可靠度为0,均不满足6σ质量水平,可靠度没达到1.000,所以桁架自动检测装置在这几个输出响应时的稳健性较差,需要对其进行6σ稳健性优化。构建桁架的可靠性稳健优化数学模型,即

式中,X为随机设计变量集;M(X)为桁架质量函数;G(X)为最大应力约束函数;D(X)为最大变形约束函数;GU为最大应力约束值,DU为最大应变约束值;XL和XU分别为设计变量X的上下限;n表示σ水平。
通过稳健性优化后,输出响应可靠度,稳健性优化后输出响应的可靠度如表6所示。由表6可以看出,横梁应力的质量水平为5.144 3σ,可靠度为0.999,纵梁应力的质量水平为4.555σ,可靠度为0.999,满足可靠性要求。

表6 稳健性优化后输出响应的可靠度
稳健性优化后,桁架总质量随迭代次数变化曲线如图10所示。由图10可以看出,当迭代次数为197次时,桁架质量为满足约束条件最小值,此时桁架质量为331.9 kg。质量分布概率随整体质量变化曲线如图11所示。由图11可以看出,桁架质量在270~450 kg为稳健性优化范围,其总分布概率大于0.99,在可靠性基础上进行稳健性优化,使优化的目标函数随设计变量的波动影响较小。
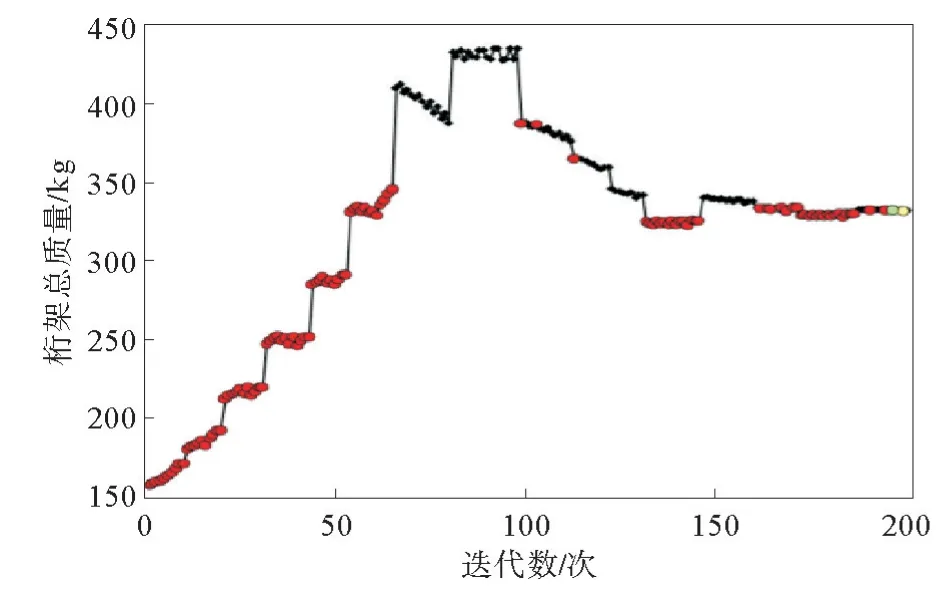
图10 稳健性优化后桁架质量变化线

图11 稳健性优化后桁架质量分布概率
对桁架自动检测装置确定性与稳健性进行优化,优化前后横梁和纵梁截面单元设计参数对比如表7所示,优化前后立柱截面单元和桁架总质量设计参数对比如表8所示。由表7和表8可以看出,在确定性优化中,横梁截面单元长度为0.141 m,侧壁厚为0.001 m,主壁厚为0.003 295 m;纵梁截面单元长度为0.138 5 m,侧壁厚为0.003 655 m,主壁厚为0.004 735 m;立柱截面单元长度为0.138 m,侧壁厚为0.002 935 m,主壁厚为0.001 m。

表7 优化前后横梁和纵梁截面单元设计参数对比

表8 优化前后立柱截面单元和桁架总质量设计参数对比
在稳健性优化中,横梁截面单元长度为0.157 m,侧壁厚为0.002 72 m,主壁厚为0.003 14 m;纵梁截面单元长度为0.145 m,侧壁厚为0.002 m,主壁厚为0.005 6 m;立柱截面单元长度为0.136 25 m,侧壁厚为0.002 m,主壁厚为0.002 m。
桁架优化结果对比如图12所示。由图12可以看出,原方案桁架的总质量为353.1 kg,经过确定性优化后,质量变为313.06 kg,结构减重达11.3%。采取可靠稳健性优化后,桁架总质量缩减为331.9 kg,结构减重为6%,虽然稳健性优化方案的效果不如确定性优化方案,但有效提高了优化的稳健性。

图12 桁架优化结果对比
4 结束语
本文主要对某桁架结构的设计变量进行灵敏度分析。选取桁架横梁、纵梁和立柱截面形状的9个设计变量,并根据设计要求确定其取值范围,推导桁架应力与应变的约束函数,进行确定性优化设计研究,优化后实现减重11.3%,采用组合近似模型对桁架进行可靠稳健性优化设计,优化后实现减重6%,在实现结构轻量化设计的前提下,有效提高了桁架结构的可靠性与稳健性。由于已有的研究主要集中于拓扑优化理论,而本文采用Hooke Jeeves算法,对桁架进行可靠稳健性分析与优化,在实际应用中,可以解决桁架用料过多问题,追求轻量化而忽视桁架的稳健性所导致的桁架性能波动和结构失效问题,后期将主要围绕桁架自动检测装置进行可靠稳健性优化设计及实验仿真验证进行研究。
