Lasso-BP组合模型在鲤鱼价格预测中的应用研究

李海涛刘昌年

(青岛科技大学信息科学与技术学院,山东 青岛 266061)

2020年,受新冠疫情的影响,我国水产养殖业出现了大规模压塘现象,养殖经营企业损失严重[1]。2021年,随着疫情的好转,消费市场逐渐复苏,而水产品市场供应严重不足,造成了水产品价格持续上涨[2]。若能对水产品价格进行预测,则能指导企业合理控制养殖规模,帮助企业减少因受市场波动造成的经济损失。近年来,国内外学者对水产品价格预测问题进行了深入研究。杨卫等人[3]基于2016年1月至2019年5月大黄鱼月度价格指数数据,提出了使用ARIMA 模型进行拟合,成功对大黄鱼价格指数做出预测;张静怡[4]基于2010—2017年上海7种主要水产品价格数据,采用Holt-winters模型对不同种类水产品进行预测;R.MAHARJAN 等人[5]提出了基于模糊CBR 模型的水产品价格预测模型,对中国水产品价格进行研究;A.P.BARTEN 等人[6]提出将逆需求体系应用于水产品价格形成研究;C.M.JOLLY 等人[7]将普通最小二乘法模型、无条件最小二乘法模型、最大似然模型和自回归条件异方模型用于水产品价格研究,对欧洲部分水产品进行分析;段青玲等人[8]提出GA-SVR 水产价格预测模型,并对价格序列进行稳定性检测,再通过GA 遗传算法优化支持向量回归模型参数,最终以最优参数为基准构建支持向量回归(support vector machines for regression,SVR)模型。基于此,本文提出一种Lasso-BP组合价格预测模型,以北京地区鲤鱼价格为例,分析价格波动成因,将影响因素通过Lasso模型进行筛选,再将关联性高的影响因素作为BP神经网络的输入变量,构建出北京地区鲤鱼价格预测模型。该研究具有一定的应用价值。

1 鲤鱼价格波动及影响因素分析

1.1 数据来源及波动分析

本文所研究的鲤鱼价格数据主要来源于北京丰台区新发地农产品批发市场、北京八里桥农产品批发市场及北京京丰岳各庄农副产品批发市场。由于各个市场报价规格不同,因此取各批发市场“＞1 000 g”规格的鲤鱼大宗报价的平均值进行研究。选取自2013年1月1日至2018年6月17日每日价格数据作为研究对象,共计1 811条数据。

2013—2017年北京地区鲤鱼月度均价走势如图1所示。由图1可以看出,鲤鱼的价格波动与季节有关,具体表现为秋冬季价格较低,春夏季价格较高,每年的6～8月处于全年峰值,其后持续下跌,直至12月价格开始回升。

图1 2013—2017年北京地区鲤鱼月度均价走势

1.2 波动成因及影响因素分析

水产品价格是水产品市场供需关系的体现[9]。在理想状态下,市场供应和市场消费直接影响价格走势。现实中,鲤鱼价格受到政策和汇率等外部因素的影响,价格走势不完全由市场供需决定,而且鲤鱼具有养殖周期长、养殖成本变化较大的特点[10],外部因素的细微变化都会对鲤鱼价格造成影响。结合市场供需关系和鲤鱼的养殖过程,可将鲤鱼价格波动成因归纳如下:

1) 生产。生产方面可从供给和生产成本2个维度进行分析。从供给方面来看,鲤鱼的产量影响鲤鱼价格,在市场需求稳定的情况下,产量越高,价格越低。产量的影响因素包含鲤鱼产量、鲤鱼养殖面积、水产苗种数量等;从生产成本方面来看,鲤鱼生产成本的提高会提高鲤鱼的价值,鲤鱼价格也会提高。影响生产成本的因素主要包含鱼塘租金、鱼苗成本、饲料成本、鱼药成本等[11]。

2) 消费。消费者对鲤鱼的需求和消费能力会影响价格。随着消费者消费理念的升级,消费者对水产品等优质蛋白质的需求日益旺盛,在一定程度上扩大了市场需求,在鲤鱼供给稳定的情况下,消费需求越大,市场行情越高[12]。影响消费需求的因素包含居民人口数量和饮食习惯等,消费者的消费能力越强,能承受的价格越高,也会促进消费需求的增长。影响消费能力的因素主要包含居民人均可支配收入、平均工资、居民人均消费支出等。

3) 流通。鲤鱼从出塘到批发市场需要经历运输过程,运输过程的成本会对鲤鱼价格产生影响,影响因素包含柴油油价和运输人员薪资等。

4) 综合因素。主要包含宏观和微观。宏观方面主要包含政府对渔业的扶持力度、生产总值、水产品产值、居民消费价格指数等因素,是政治经济的综合体现[13]。微观方面主要包含产区平均气温、平均降水量及鲤鱼价格的周期性波动等因素[14]。

通过对波动成因的分析,选择北京地区平均气温、降水量和鲤鱼产量等19个因素为研究对象,影响因素及数据来源如表1所示。

表1 影响因素及数据来源

2 基于Lasso-BP鲤鱼价格模型的构建

2.1 基于Lasso-BP鲤鱼价格模型原理

基于Lasso-BP鲤鱼价格模型主要包括Lasso回归模型和BP神经网络两部分,Lasso-BP组合模型结构如图2所示。图中Lasso回归部分的x1…x19为待筛选的19个影响因素,BP神经网络部分的x′1…x′9为筛选后的9个影响因素,H1…H10为10个隐含层节点,输出层节点Y为鲤鱼价格。

图2 Lasso-BP组合模型结构

首先使用Lasso回归模型对影响因素变量进行筛选,再将筛选之后的影响因素作为BP神经网络的输入,将鲤鱼价格作为输出。影响因素数据通过隐含层的非线性变换之后输出价格,若输出价格与真实价格不相符,则进入误差反传过程,将误差传递至各层的节点,以误差为依据重新调整各节点之间的权值,直至找到误差最小的参数,完成神经网络训练[15]。

将影响因素数据输入到训练之后的模型中,即可输出预测价格。使用Matlab 进行编程,Lasso-BP组合模型实现过程如图3所示。

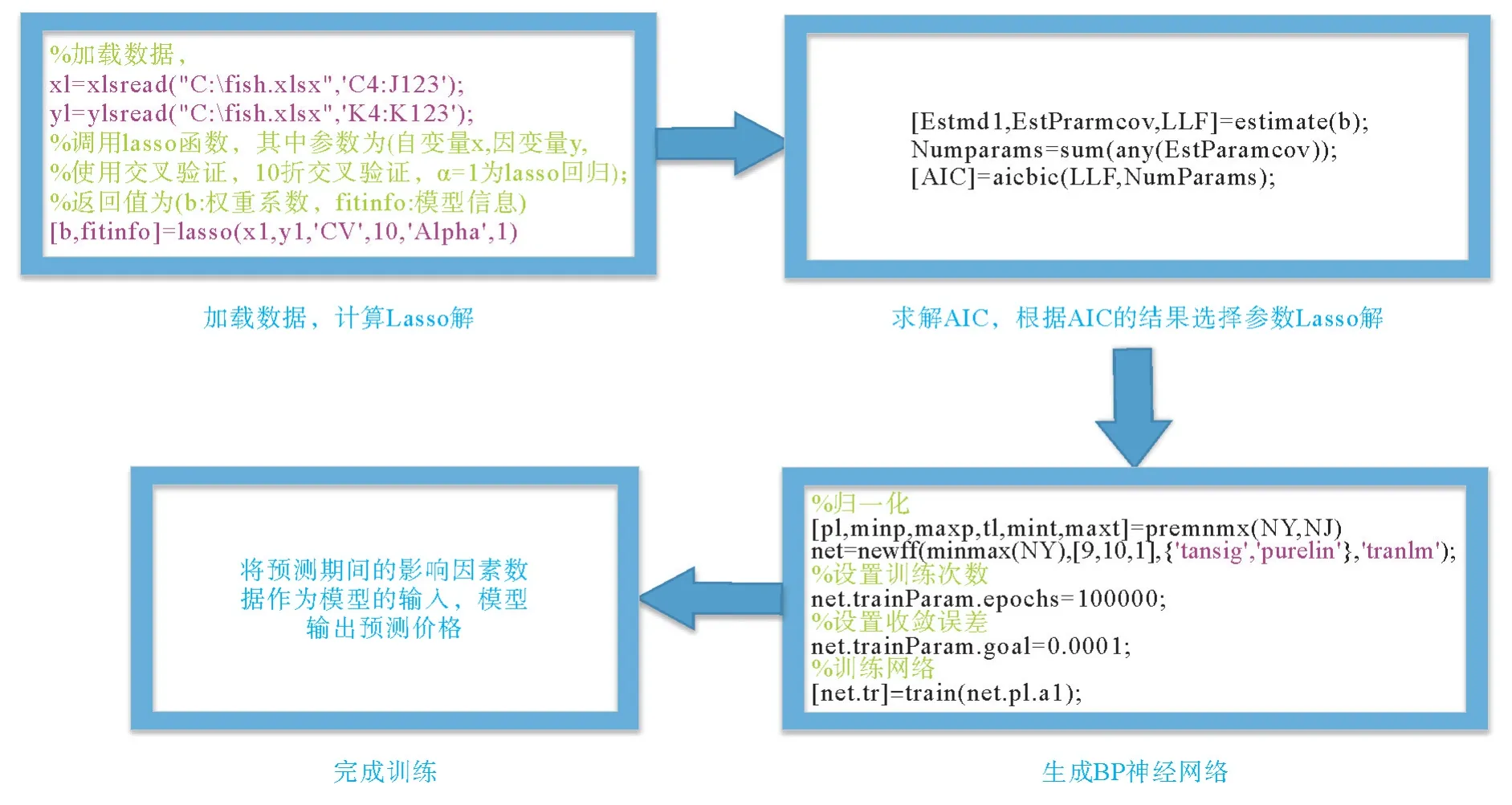
图3 Lasso-BP组合模型实现过程

2.2 变量选取及数据预处理

根据以上分析,选取19个对鲤鱼价格造成影响的变量,即平均气温x1、降水量x2、柴油价格x3、居民人均可支配收入x4、社会平均工资x5、居民人均消费支出x6、年末常住人口x7、水产品类居民消费价格指数x8、北京市生产总值x9、渔业总产值x10、农用柴油使用量x11、地方财政农林水事务支出x12、鲤鱼产量x13、鲤鱼养殖面积x14、水产苗种数量x15、淡水加工品总量x16、渔业从业人员数量x17、受灾害水产品损失数量x18、渔业灾情造成的经济损失x19,并选取2013年1月至2017年5月的影响因素与价格数据作为训练样本,部分样本数据如表2所示。

表2 部分样本数据

由于鲤鱼价格受到多种因素的影响,各个因素的单位不一致,因此需要对原始数据进行中心标准化处理[16],使不同维度的特征拥有相同的影响尺度。中心标准化后的数据计算过程为

式中,x为原始数据;μ为原始数据均值;σ为方差。

构建鲤鱼价格Yt影响因素的线性回归模型为

式中,β1…β19是影响因素的回归系数;εt是一系列服从标准正态分布的干扰项;β取常数8。

2.3 Lasso回归筛选影响因素

将中心标准化之后的数据进行Lasso求解,经过28次迭代得到所有的Lasso解,使用赤池信息准则(akaike information criterion,AIC)确定最佳模型[17]。赤池模型通过在似然函数添加惩罚项的方式描述模型的精度[18],根据赤池最小值A可以从一系列不同模型中确定最佳模型,即

式中,d为参数数量,d＝19;n为观测数,n＝28;R为残差平方和(residual sum of squares,RSS)。残差平方和计算方法为

式中,yi为实际值为估计值。

求解后,Lasso回归模型参数估计如表3所示。由表3可以看出,在第9次Lasso迭代时,赤池信息值A达到最小值,此时模型拟合最佳。选择第9次迭代结果作为变量筛选依据,去掉系数为0的参数,最终选取平均气温、居民人均可支配收入、居民人均消费支出、水产品类居民消费价格指数、渔业总产值、地方财政农林水事务支出、鲤鱼产量共9个变量作为BP神经网络的输入层节点。

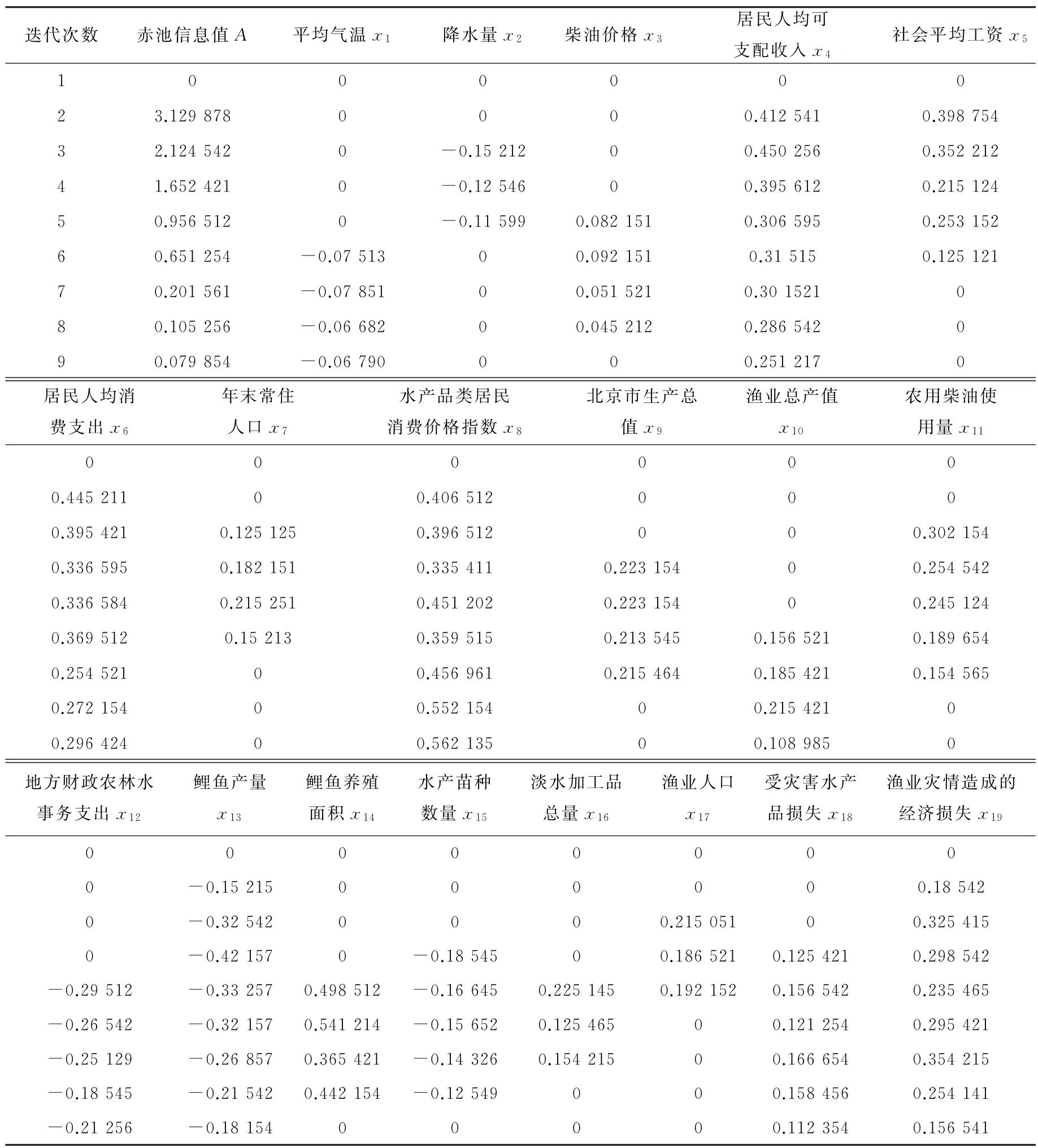
表3 Lasso回归模型参数估计

2.4 训练BP神经网络

为了避免神经网络收敛慢的问题,需要对样本数据进行归一化操作[19]。采用零均值归一化方法,将数据映射到[0,1],归一化后的数据计算方法为

式中,μ为原始数据的均值;σ为原始数据的标准差;x为原始数据。

选择2013年1月1日至2017年9月31日数据作为训练样本,构建BP神经网络需确定网络结构、激励函数和隐含层节点数[20]。将Lasso回归模型筛选出的9个变量作为BP神经网络的输入层节点,输出层节点为鲤鱼价格,隐含层和输出层的激励函数分别选择tan-sigmoid函数线性传递函数purelin。隐含层节点数的计算公式为

式中,N为输入层节点数,N＝9;M为输出层节点数,M＝1;常数a范围为[0,10]。经计算,隐含层节点数应在[3,14]之内。将训练次数上限设置为10 000,误差目标设置为10－8,隐含层节点数分别设置为3～14,生成BP神经网络,BP神经网络训练过程如图4所示。

图4 BP神经网络训练过程

将隐含层节点数不同的神经网络进行检验,不同隐含层节点数神经网络均方误差如图5所示。由图5可以看出,当隐含层节点数为10时,均方误差(mean squared error,MSE)最低,模型性能最佳。BP神经网络的拓扑结构设定为9-10-1,重新训练神经网络,在进行162次迭代后,均方误差满足预设的误差目标10－8,训练停止。BP神经网络迭代过程如图6所示。

图5 不同隐含层节点数神经网络均方误差

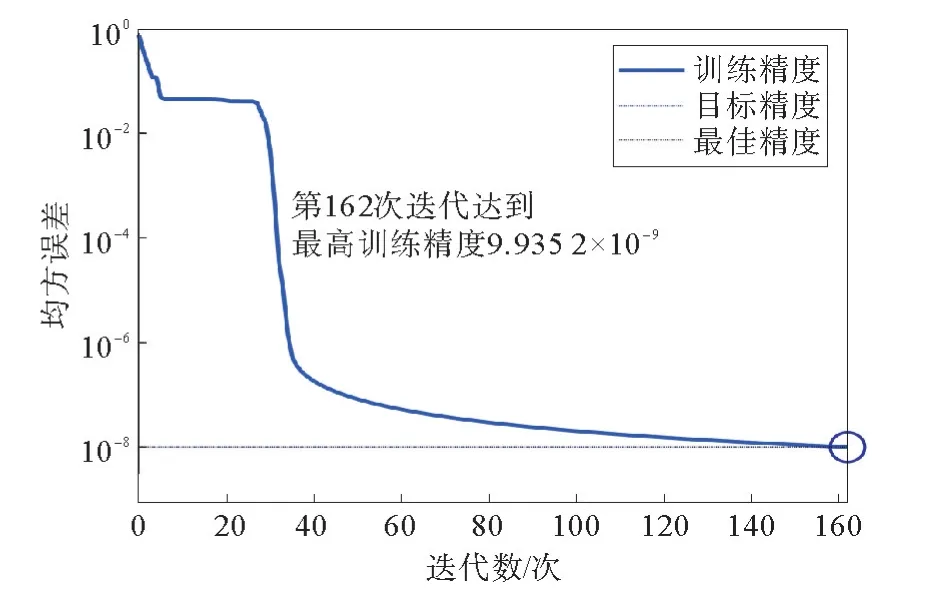
图6 BP神经网络迭代过程

3 实验结果分析

3.1 预测结果分析

选择2017年10月1日至2018年6月17日数据作为测试样本,对测试样本进行归一化处理。使用已构建的BP神经网络对2017年10月1日的价格进行预测,再将预测结果加入到训练样本中,重新训练神经网络,以此类推,直至完成对2018年6月15日的预测,共获得260条预测结果。对输出结果进行反归一化处理,获得价格预测值,Lasso-BP组合模型部分预测结果如表4所示。

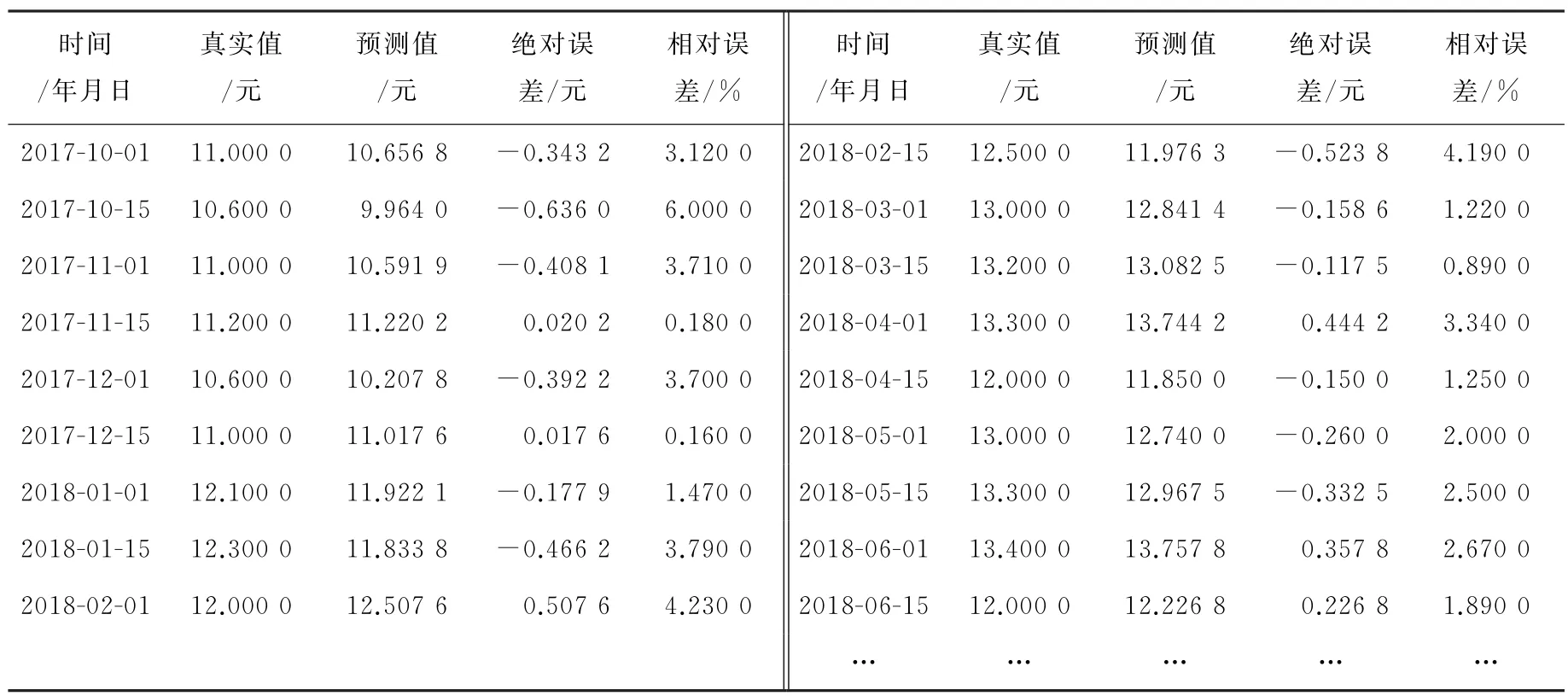
表4 Lasso-BP组合模型部分预测结果

在260条预测数据中,有30条预测数据相对误差低于1%,70条数据介于1%与3%之间,120条数据在3%～5%之间,40条数据大于5%,预测值与真实值整体平均误差2.59%,模型预测精度较高。真实价格与预测价格拟合情况如图7所示。

由图7可以看出,在260条预测数据中,有132条预测值大于真实值,128条预测值小于真实值,误差偏向不明显。在价格波动趋势方面,有251条预测数据与真实情况相同,9条预测数据与实际情况相反,准确率96.53%。在价格波动幅度方面,预测结果的波动幅度与真实数据基本相同,预测结果可满足实际生产工作中的需要。

图7 真实价格与预测价格拟合情况

3.2 Lasso-BP与其他模型实验结果对比

本研究采用Lasso-BP组合模型,并与无Lasso的BP神经网络和ARIMA 差分整合移动平均自回归模型进行对比,选择均方误差MSE、平均绝对误差MAE和回归方程确定性系数R2作为不同模型的评判方法,不同模型指标对比结果如表5所示。

由表5可以看出,通过对3种模型比较可以看出,ARIMA 模型的MAE远高于其他2种模型,已经无法满足实际需求,而Lasso-BP 组合预测模型和BP神经网络模型的MEA 较低,预测效果较好;在回归方程确定性系数R2方面,Lasso-BP组合预测模型最大,拟合效果最好;BP神经网络模型与Lasso-BP组合预测模型MSE均好于ARIMA 模型。

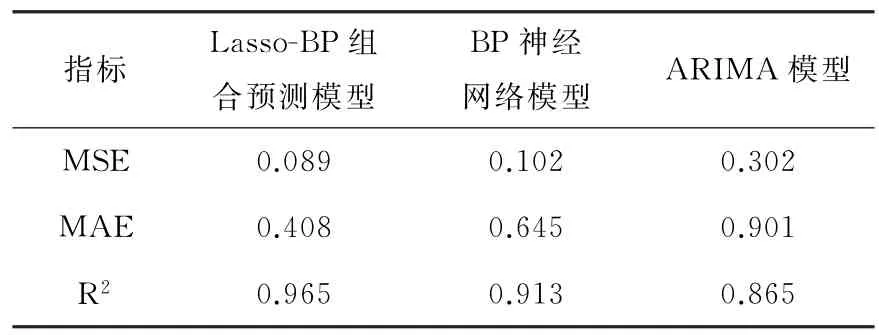
表5 不同模型指标对比结果

4 结束语

本文提出了一种使用Lasso-BP组合模型进行鲤鱼价格预测的方法,并选择2013—2018年北京地区鲤鱼价格及影响因素数据进行试验,实验结果证明本文提出的价格预测模型能准确预测鲤鱼价格。在实验过程中,由于研究方法的局限性,未考虑很多难以量化的影响因素,如政策因素、社会突发事件、自然灾害事件等,可能会影响模型的预测精度。与研究价格自身的波动规律不同,本文从消费、生产、流通等不同环节选择多个影响因素进行研究,获得了各个影响因素与鲤鱼价格之间的映射关系,构建的价格预测模型符合水产品价格波动成因。本文提出的组合预测模型实现了通过历史数据对未来鲤鱼价格做出预测,为养殖企业提供生产指导,帮助企业规避市场因素造成的经济损失。接下来的研究重点是将寻找合适方法对难以量化的因素进行研究,并结合GA 遗传算法,对BP神经网络的初始化权值和阈值进行寻优,加快BP神经网络收敛,提高预测精度,进一步优化模型。