嫦娥五号月面上升和下降段实时轨道确定

黄普，张重阳，李海玥，王帆

宇航动力学国家重点实验室,西安 710043

1 引言

在嫦娥五号任务中，探测器首次进行月面上升。在这个环节中由于距离远、信号弱，上升过程将完全依靠自身系统，这对器上导航，制导与控制(guidance,navigation and control，GNC)系统是一个考验，同时，如何利用外测数据实时确定探测器位置也是一个重要问题。由于月面上升过程采用自主GNC模式，受力复杂，地面中心很难建模，传统的动力学定轨方式将不再适应，众多学者[2-4]均给出非动力学的定轨方法，其中Song在近地卫星定轨中，采用样条法逼近航天器的轨道[5]。昌胜骐同样采用样条法，对落月过程的轨道进行了分析[6]。黄勇等利用统计定轨方法对嫦娥三号任务软着陆和返回过程的轨道进行了事后解算[7-10]，这些方法采用参数化建模的形式，利用样条函数逼近轨道，实现了高精度统计定位，但主要问题在于样条函数的节点选择需要人工干预，并不适合实时定位，同时，几种方法均为几何定位，测量数据质量对精度影响大，特别是轨道曲线的平滑性受测量野值影响很大。

为此本文分析探测器月面上升和下降过程，建立自适应当前统计模型，利用无迹卡尔曼(unscented kalman filter，UKF)方法进行实时定位，考虑到运动过程的复杂性，可通过自适应模型进行非动力学模型建模。通过对嫦娥五号探测器月面上升下降数据进行测试，证实了该方法的有效性，为深空探测三向测量跟踪定位技术提供新思路。

2 实时自适应轨道确定方法

2.1 三向测量预测值计算

目前，深空探测航天器的外测数据除了常用的甚长基线干涉测量(very long baseline interferometry，VLBI)数据[9,10]外，还包括三向测量数据[11,12]，其主要通过主站发送上行信号，经应答机转发后，由副站接收信号，获得双程测距和，当两个副站及主站同时接收到下行信号后，传统方法通过几何方式进行定位计算，测量原理如图1所示。但该种方式受测量精度影响很大，且通常为事后计算。本文从实时定位需求出发，将自适应模型引入三向测量模型，进而完成滤波计算。

图1 三向测量原理图Fig.1 Three-way measurement schematic diagram

图中SI，S2和S3分别代表3个测站(S1为主站，S2和S3为副站)，S1发上行信号时刻为T0，T0经卫星转发机处理后，发射下行信号时刻为T1，S1按收到下行信号时刻为T4，S2接收到下行信号时刻为T2，S3接收到下行信号时刻为T3。

考虑到UKF滤波方法不需要将测量值线性化，可将观测模型直接建立在观测坐标系(如东北天测量坐标系)下，且以距离和作为观测量。

考虑到三向测量的时标(记为Te)均为下行测站接收时刻，其对应的探测器时间(记为Tn)、上行测站发送站时间(记为Ts)，由于电波传播时延，必不相同，为此，滤波计算中需要根据探测器当前状态矢量X及光行时公式迭代计算三个时标，τ1，τ2为光行时，指电磁信号在发射和接收之间传播的时间间隔。测量解算如图2所示。

2.3 急性呼吸窘迫综合征炎症损伤患儿SIRT6与炎症因子及动脉血气指标相关性 采用Pearson相关系数分析显示，肺泡SIRT6含量与TNF-α、IL-6、PaCO2呈显著正相关，与PaO2、PaO2/FiO2呈显著负相关(P<0.05)。见表3。

图2 距离和解算示意图Fig.2 Distance sum solution diagram

迭代出三个时标后，由发端站、收端站大地坐标即可计算出两站分别在Ts、Te时刻的地心惯性系位置rs、re，又由滤波器状态外推可计算出Tn时刻探测器的位置rn，这样即可得到Te时刻的距离和预测值为：

r=|rn-re|+|rn-rs|

(1)

以三向测量的三条基线d11，d12，d13为例，计算三向测量的预测值方程如下：

(2)

(3)

(4)

2.2 当前统计滤波算法

在机动目标跟踪计算中，受力复杂很难建立高精度动力学模型的情况下，通常采用运动学定轨方式，主要包括：多项式模型、当前统计模型及相关改进方法[13-15]。

以当前统计模型为例，其主要采用修正瑞利分布描述目标机动加速度，能准确体现目标的机动特性，可定义系统状态矢量为：

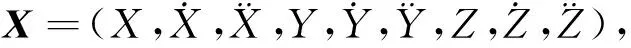
X(k+1|k)=f(X(k|k),W(k))=

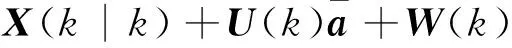
(5)

(6)

(7)

(8)

2.3 自适应计算

当前统计模型的性能需要依靠加速度最大幅值与机动常数的准确设置。通常解决方法为事前分析，分段设置，该方法能在一定程度上解决问题，但对滤波性能的影响依然存在，且当目标机动与事先不一致时，会严重影响滤波性能，为此本文采用自适应[15]的方式实时在线计算机动参数。

(1)加速度最大幅值计算

(9)

(2)机动常数计算

加速度的变化与机动常数存在关联。可通过累积增量的方法进行计算。设置采样间隔为Δt，则加速度增量Δak=ak-ak-1，具体公式如下：

(10)

同样，实际计算中，需要引入渐消因子λb∈(0,1)和λα∈(0,1)提高系统的稳定性并限制αk的大小。渐消因子可根据公式(11)进行计算。

(11)

3 算例分析

为了验证算法的可行性，分别使用月面上升和下降数据进行测试。其中月面上升过程由于没有三向测量数据，可根据事后数据仿真观测数据进行测试。月面下降过程全程采用实测三向测量数据进行测试，由于没有标准轨道评价该弧段轨道的外符合精度，可通过内测弹道作为标准轨道。

(1)仿真数据月面上升轨道计算

月面上升过程发生在北京时间2020年12月3日23时10分，持续时间大约400 s，将事后多源融合轨道作为标准轨道，生成三向测量数据，采样率设置为1 s，测距噪声标准差设置为5 m。为了验证算法的有效性，分别采用传统的多项式滤波方法、本文提出的自适应滤波方法和几何定位方法计算的上升过程高度变化，计算高度变化曲线和定位偏差曲线如图3、4所示，其中横坐标表示相对时间，起始点为23时10分，高度变化图中设置月球参考半径为1 737 400 m。

图3 不同算法的高度变化曲线Fig.3 Height change curves of different algorithms

图4 不同算法定位误差曲线Fig.4 Positioning error curves of different algorithms

(2)实测数据月面下降轨道计算

月面下降过程发生在北京时间2020年12月1日22时57分，持续时间大约12 min，三向数据的三个测站分别为喀什、三亚、佳木斯。分别采用多项式滤波方法、自适应滤波方法和几何定位方法计算的下降过程高度变化曲线如图5所示，其中横坐标表示相对时间，起始点为22时57分，高度变化图中设置月球参考半径为1 737 400 m。

图5 实测数据不同算法的高度变化曲线Fig.5 Height change curves of different algorithms for measured data

从上图3～5可以看出，几何定位方法受制于三向测量精度，计算曲线存在震荡；两种滤波方法同样受制于三向测量精度但抗差性要明显好于几何定位方法，多项式滤波方法在滤波起始阶段和机动过程中存在适应性差的问题，而本文提出的自适应滤波方法效果最好。另外，当采用两个站进行跟踪时，滤波直接发散，定位误差曲线如图6所示。

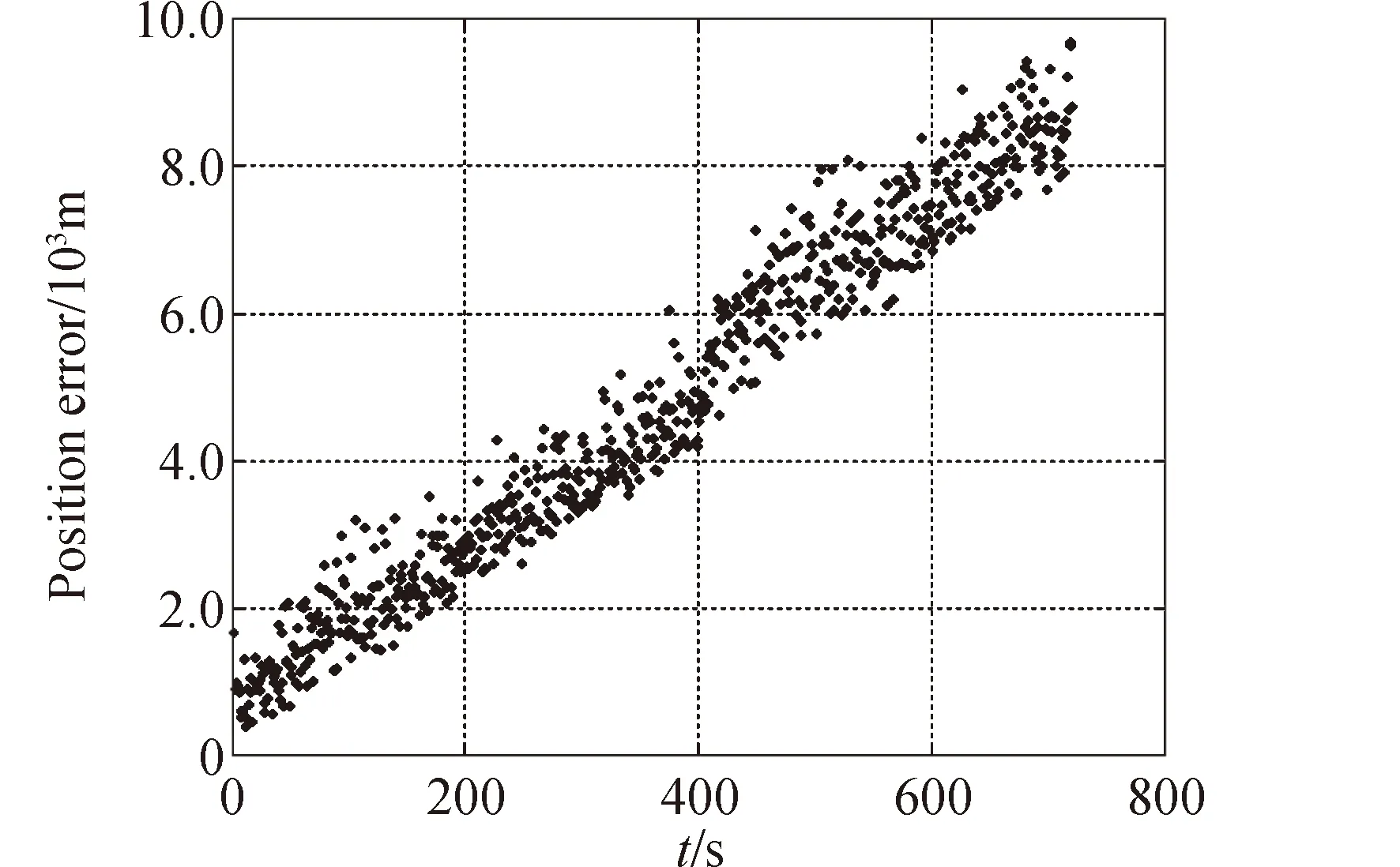
图6 双站滤波定位误差曲线Fig.6 Two-station filtering positioning error curve

4 结论

本文对深空探测中常用的三向测量方式进行了阐述，并提出自适应多项式模型的三向测量滤波算法，从嫦娥五号的月面上升下降数据滤波计算结果可得到以下结论：

1)本文给出的自适应当前统计滤波方法是可行的，但测量结果受测量精度影响较大，且至少要有3个站才能正确定位。

2)对于三向测量数据滤波，运动学滤波算法抗野值能力和稳定性要好于几何定位方法。

可以看出，虽然三向测量数据是深空探测的一类重要观测数据，但此类数据源对测量精度较为敏感，定位精度受测量精度影响明显，需要联合其他数据源进行融合计算提高定位精度。