模块化空间可展开天线支撑桁架结构的热-结构分析

2022-11-21金路张飞扬田大可

中国空间科学技术 2022年5期

金路，张飞扬，田大可

1. 沈阳建筑大学土木工程学院，沈阳 110168 2. 沈阳建筑大学机械工程学院，沈阳 110168

1 引言

模块化空间可展开天线是航天和国防领域传递与获取信息的重要核心装备[1-3]，是近二三十年来随着航天科技的快速发展而产生的一种新型空间结构，广泛应用在空间通信、军事侦察、对地观测、导航等领域[4-6]。随着深空探测技术对卫星天线结构的精准服役需求不断提高，天线支撑结构作为空间可展开天线中的核心部件，在轨服役时遭遇恶劣环境影响及动力响应问题日益凸显，其中天线结构从日照区到阴影区绕地飞行受到热辐射影响而诱发振动及变形等热力学问题最为常见。

热诱发变形振动最早由Boley从理论上预言，并给出参数判断依据[7]。之后国内外学者逐渐关注空间结构在热环境下的热力学响应，Thornton等根据HST太阳翼弯曲振动，发现了结构动力响应与瞬态温度场的相互耦合，给出了弯曲振动稳定性的判断依据[8]；Namburu R等研究发现受一般线性与非线性温度作用下受弯构件的动力响应存在显著差异[9]；Johnston J D等研究了带有柔性附件的航天器热诱导姿态动力响应振动，确定了柔性附件的热响应时间与结构响应时间的比值有关[10]；张淑杰针对直径5 m的抛物面可展天线进行了温度场分析、热应力分析和结构变形仿真分析[11]；丁勇等通过傅里叶-有限元法构造空间薄壁圆管结构瞬态温度场计算，为分析复杂空间结构的瞬态温度场和热变形提供了行之有效的方法[12]；Rodriguez J I等对TES(对流层发射光谱仪)的热低温系统开发了热低温技术，最大限度地提高了仪器的整体性能[13]；范立佳等通过Lagrange非线性有限元法，研究了航天器柔性附件等结构在轨工作时的热-动力耦合[14]；刘劲等对星载铰接肋天线结构进行了热振动有限元研究，结果表明热致振动导致天线结构形面精度受到影响[15]；吴江等通过绝对节点坐标法提出了基于柔性多体系统的新方法，研究了空间结构展开的热弹性效应[16]；李俊兰等在近地轨道和地球同步轨道两种不同的高度下，研究了太阳翼在空间热流作用下热响应[17]；Abbas等针对暴露在温度场超音速飞行中的面板，开发了可变厚度的三维矩形板单元[18]；苏新明等分析了柔性空间桁架在不同结构参数下的热致振动[19]；孔祥宏等通过提出的有效位移法对柔性太阳翼计算分析了结构的热响应，为结构优化及在轨安全稳定设计提供参考[20]；孙远涛研究了星载螺旋天线结构在轨工作时复杂恶劣环境规律，对结构强度和动力特性进行了仿真分析，从而反馈指导天线结构设计[21]；贠海亮等对环形可展天线进行了热-结构分析，结果表明天线结构在轨工作时进出阴影区受到非均匀温度场作用会发生显著的结构整体变形[22]；武聪魁等对环形可展天线结构进行了热-结构分析，研究发现温度场对结构形面精度和张力影响显著[23]。综上，大型空间结构热-结构耦合问题不可忽视，对卫星结构振动及变形等力学性能影响显著[24-25]。而模块化构型使空间可展开天线结构口径扩展到百米成为可能，这将导致热致变形影响网面精度及结构稳定性问题更加明显。

对模块化空间可展开天线支撑结构在空间热交变环境下进行热-结构分析，研究天线结构各弦杆及拉索的热应力及结构关键点位置热致变形发展趋势。对比分析不同约束位置下天线结构随时间历程的热致变形的发展，为模块化空间可展开天线结构的防护与设计提供依据。

2 有限元模型及验证

2.1 天线支撑桁架结构

天线结构是模块化空间可展开天线展开锁定后的支撑背架，由多个六边形模块根据天线网面精度拓扑排列而成[26-27]。首先由上下弦杆、斜腹杆和竖杆组成肋单元(图1)，再由六个肋单元和拉索组成单个六边形模块(图2)，将单模块拓扑形成3圈19个模块的双层抛物面天线支撑桁架结构，尺寸为4 800 mm×5 196 mm。

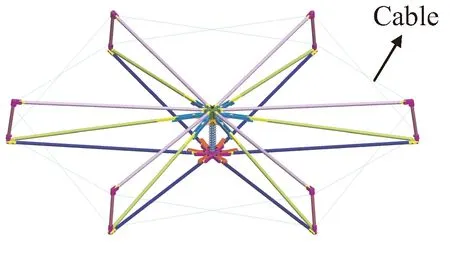
图2 单模块单元Fig.2 Single module unit

如图3所示，其中双层抛物面天线结构上层内侧凹面为上弦杆，下层外侧凸面为下弦杆，其第一圈有1个模块，第二圈有6个模块，第三圈有12个模块，该结构各模块的拓扑位置、圈数及标记点见图4。图4中BB′表示两模块拼接竖杆位置，该结构所有杆件为空心2A12铝合金圆杆，竖杆外径为12 mm，内径为10 mm；上下弦杆和斜杆外径为10 mm，内径为8 mm；拉索为1 mm直径钢丝索。

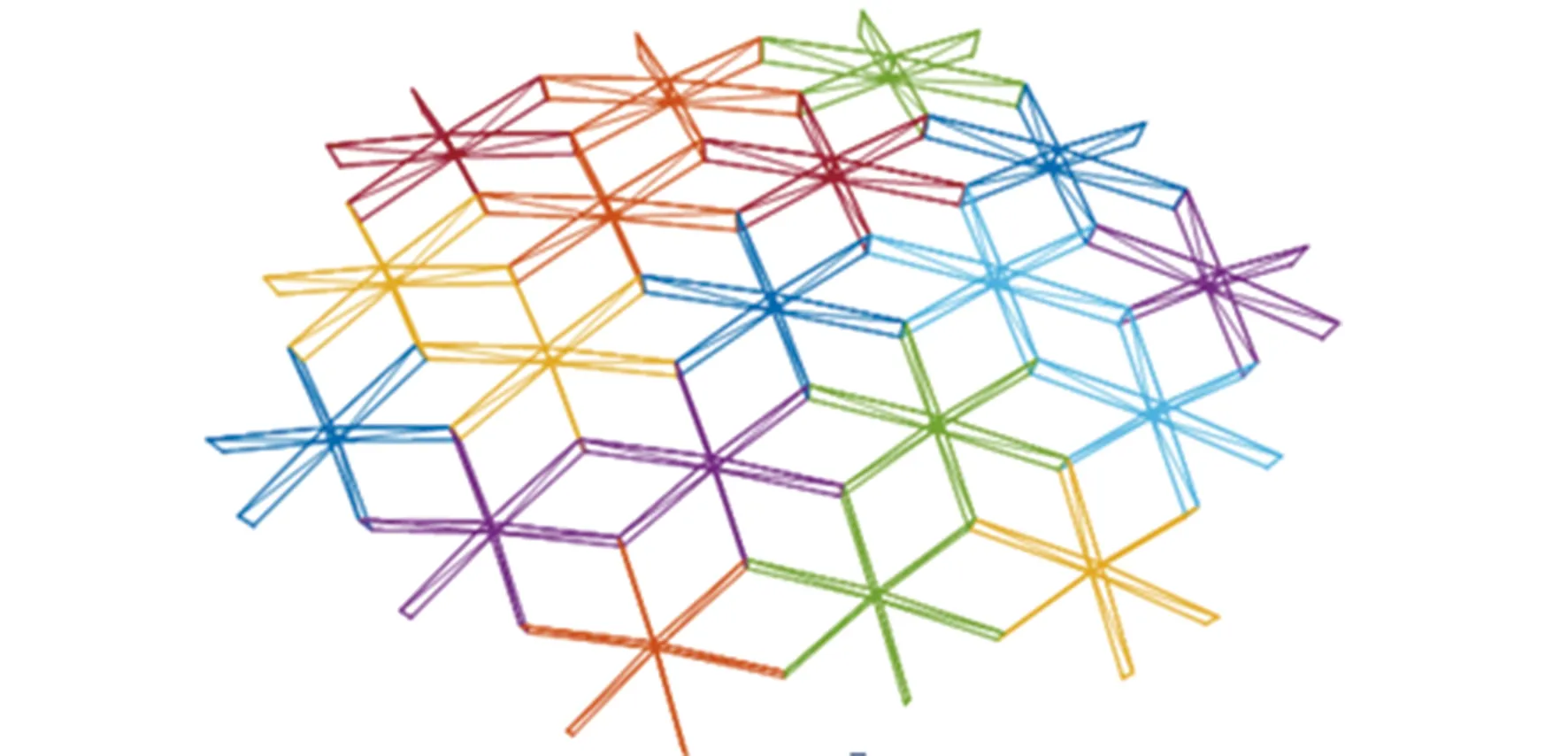
图3 天线支撑桁架结构Fig.3 The antenna support truss structure

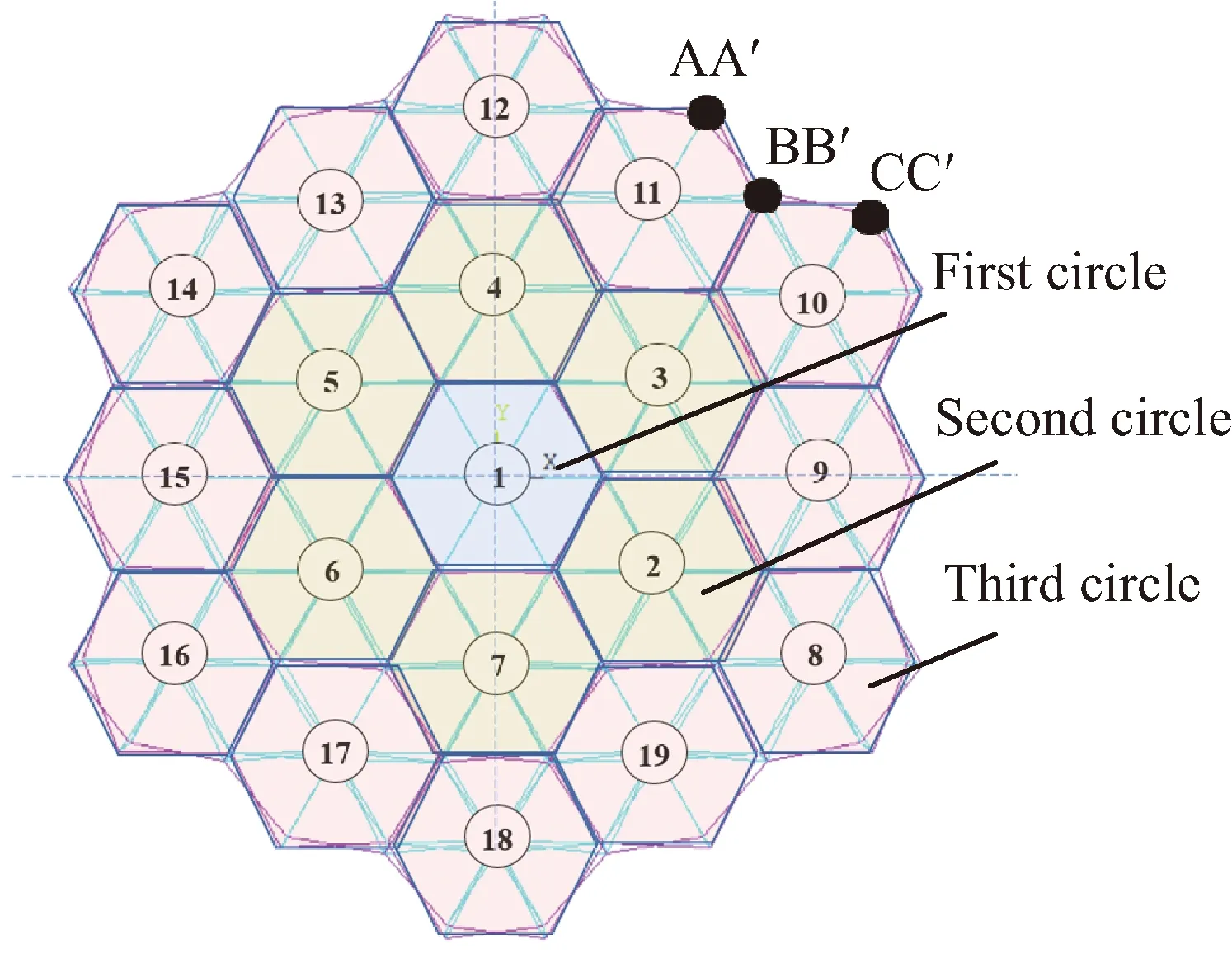
图4 模块位置分布及圈数拓扑图Fig.4 Module location distribution and hierarchy topology

2.2 模型的建立

利用ANSYS APDL有限元软件建立图5所示天线支撑桁架结构有限元模型。热应力分析中对最外层模块之间竖杆连接BB′处进行位移和转角约束，作为天线与卫星伸展臂连接展开点。天线结构在展开后，通过拉索作用保证结构整体稳定即为超静定结构。各杆件之间为刚性连接，天线结构杆件的材料参数见表1。

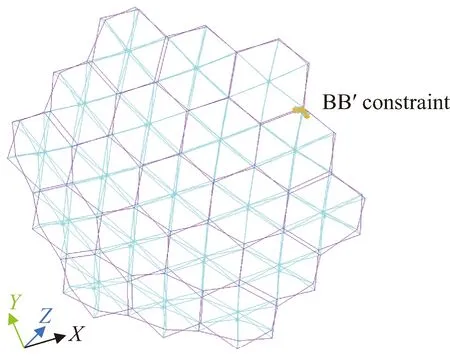
图5 模块化可展天线支撑桁架结构有限元模型Fig.5 Finite element model of modular deployable antenna support truss structure

表1 材料参数表

2.3 结构模型验证

根据文献[28-29]中2圈7模块天线支撑桁架结构模态试验(图6)，建立2圈7模块天线支撑桁架结构有限元模型(图7)，运用子空间法对该模型进行模态分析，得到天线结构的固有频率及振型图，并与试验结果进行对比，验证天线支撑结构有限元模型的准确性。采用beam188单元模拟天线结构各个弦杆，link10单元模拟拉索，并施加200 N预紧力，mass21单元模拟集中质量。

图6 7模块天线支撑桁架结构试验装置Fig.6 Experiment apparatus of 7-module antenna support truss structure

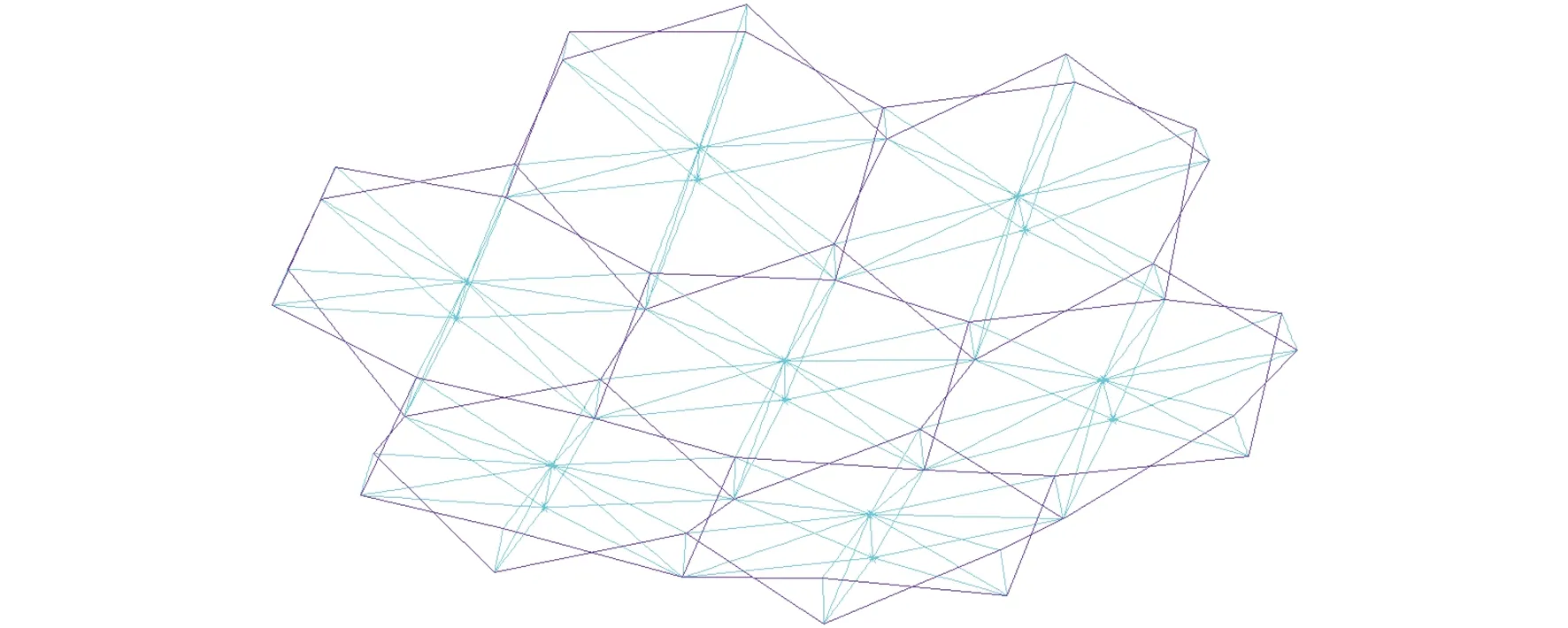
图7 7模块天线支撑桁架结构有限元模型Fig.7 Finite element model of 7-module antenna support truss structure

表2为该结构试验实测值与有限元分析计算的前四阶固有频率对比。图8为该结构通过试验激振器得到的前两阶振型图与本文有限元模拟结果对比。由图8和表2可以看出，两种方法得到的结构前两阶振型一致，二至四阶固有频率相差不大。一阶固有频率相差10.59%，分析原因可能为天线结构展开锁紧装置导致杆件点位误差所致，但此有限元计算结果与文献[20]中对结构模型进行有限元自证结果一致，说明对此类天线结构采用该有限元建模方法的正确性。

表2 有限元结果与试验结果比较

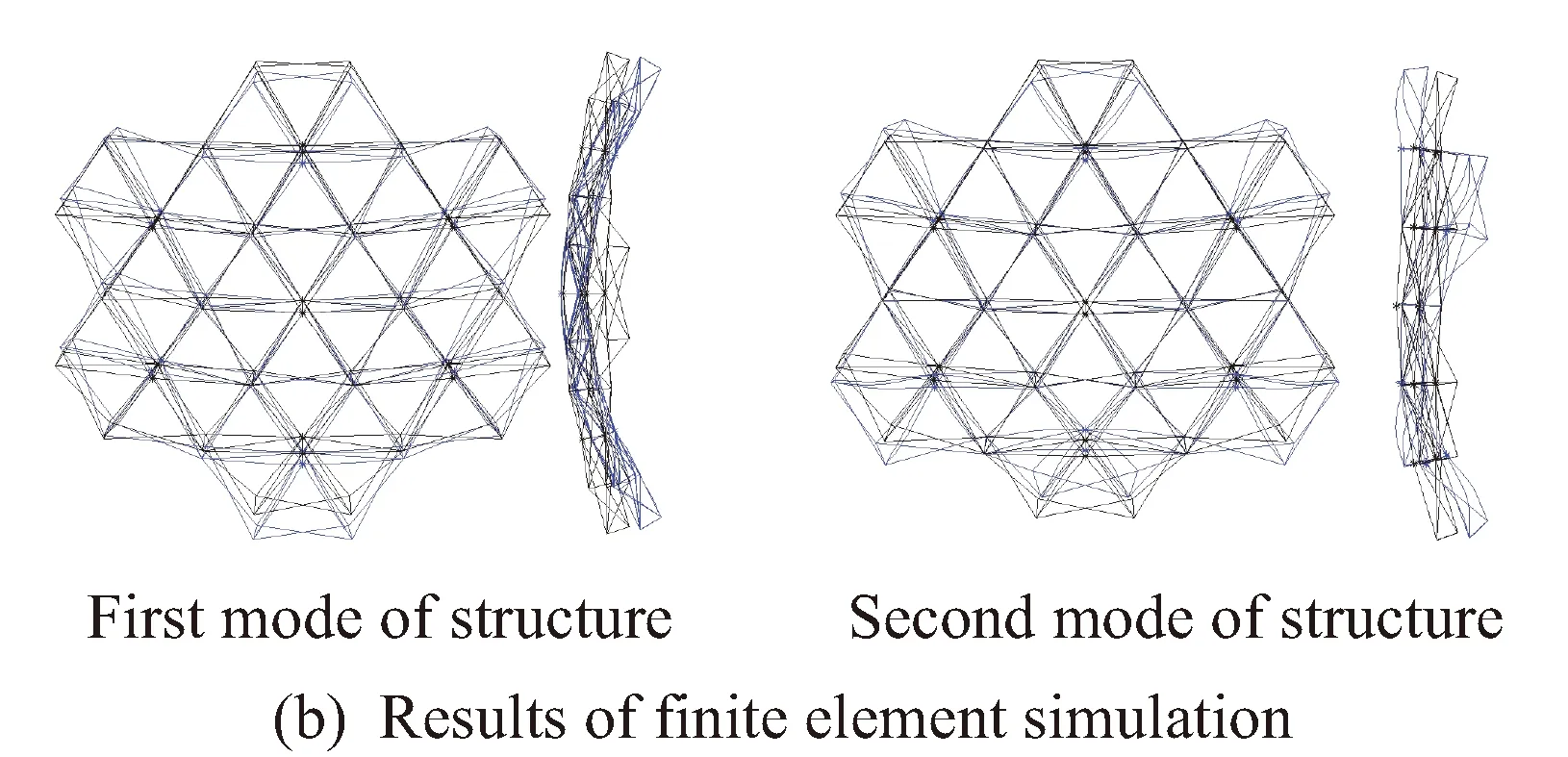
图8 试验与有限元分析比较Fig.8 Comparison between experiment and simulation

2.4 热分析模型验证

采用ANSYS有限元软件对文献[30]中的网架结构非均匀温度场试验进行瞬态热分析全过程模拟(图9)，得到该网架结构日照下非均匀温度场分布，并与试验结果进行对比，从而验证结构热分析模型的准确性。模型采用link31单元模拟结构各杆件(图10)，杆件材料为钢管，钢材的热物理特性见表1。

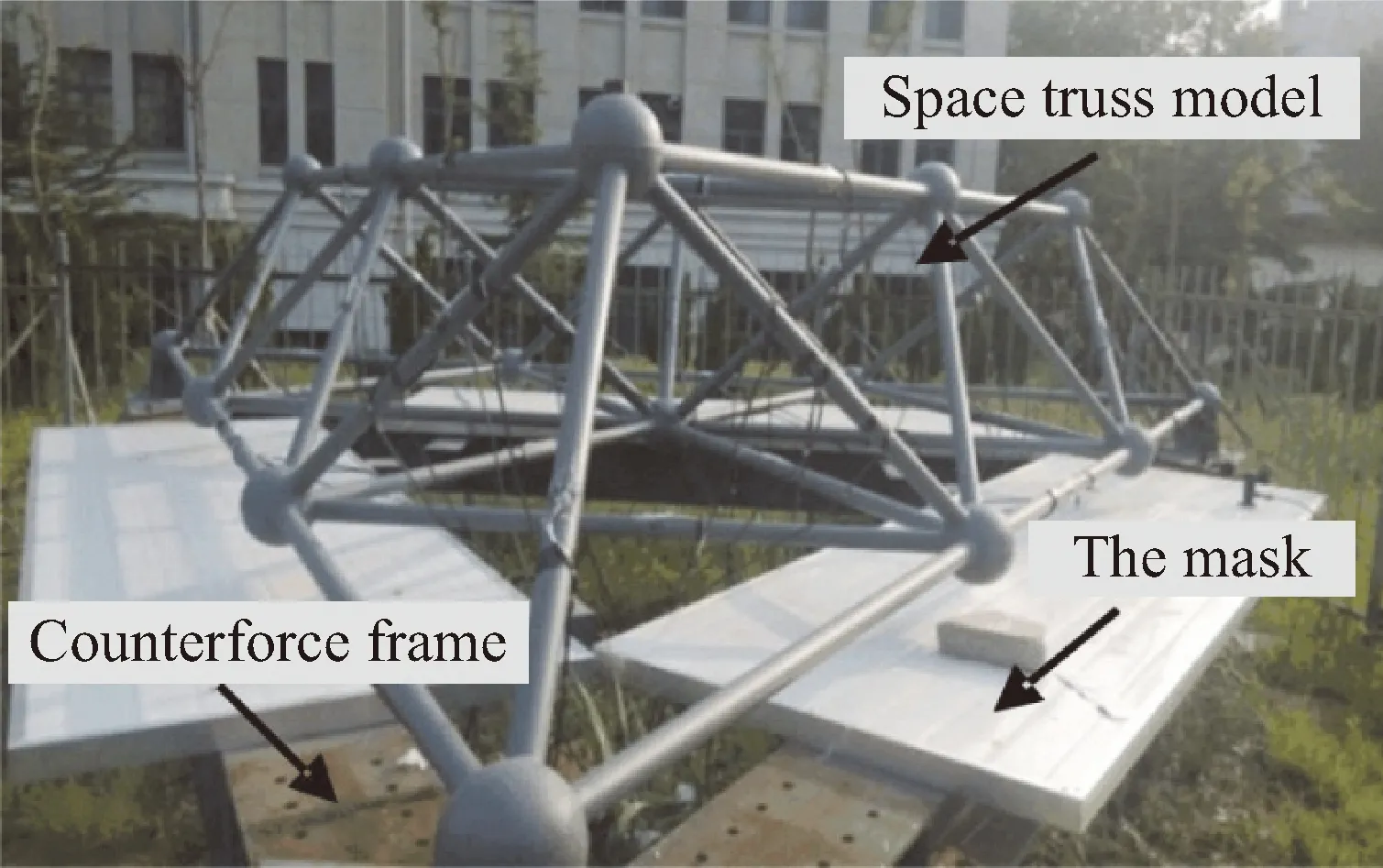
图9 钢结构空间网架结构热分析试验装置Fig.9 Experiment apparatus for thermal analysis of steel structure space grid structure

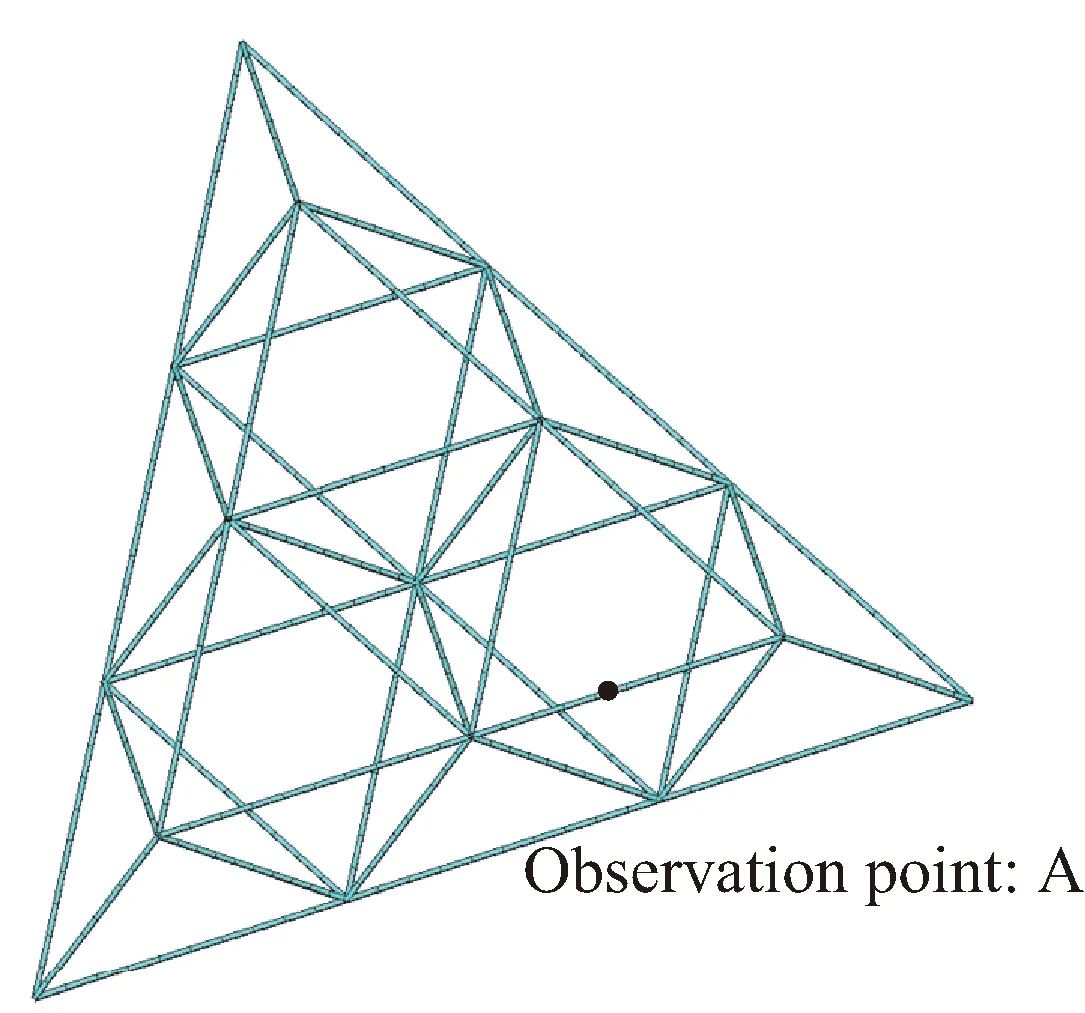
图10 钢结构空间网架结构有限元模型Fig.10 Finite element model of spatial steel grid structure

图11为网架结构测点A处(见图10)24 h网架结构试验实测值与有限元模拟值温度变化趋势对比；整个网架结构在经历了14 h的温度场试验后各杆件温度场分布对比见图12。可以看出，采用ANSYS有限元软件对网架结构进行热分析得到的温度场分布与试验实测温度场分布基本相同，24 h内某测点的温度变化趋势也与试验值吻合较好。在试验开始6 h后测点A的应力值相差最大，其他时刻平均相差约4%，由此说明采用该方法建立天线支撑桁架结构等类似结构的热分析模型的正确性。

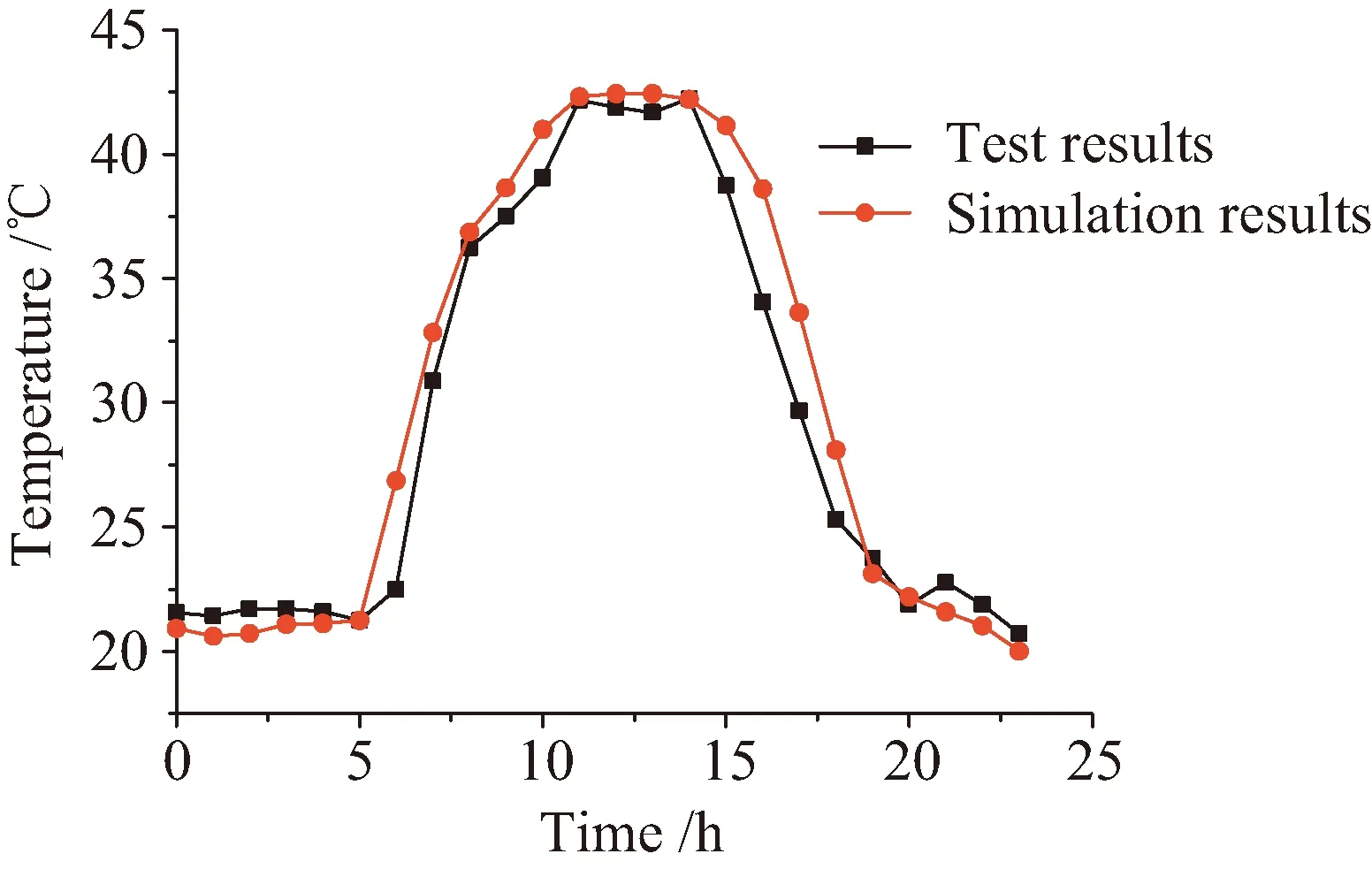
图11 试验值与模拟值对比Fig.11 Comparison between simulation and experiment

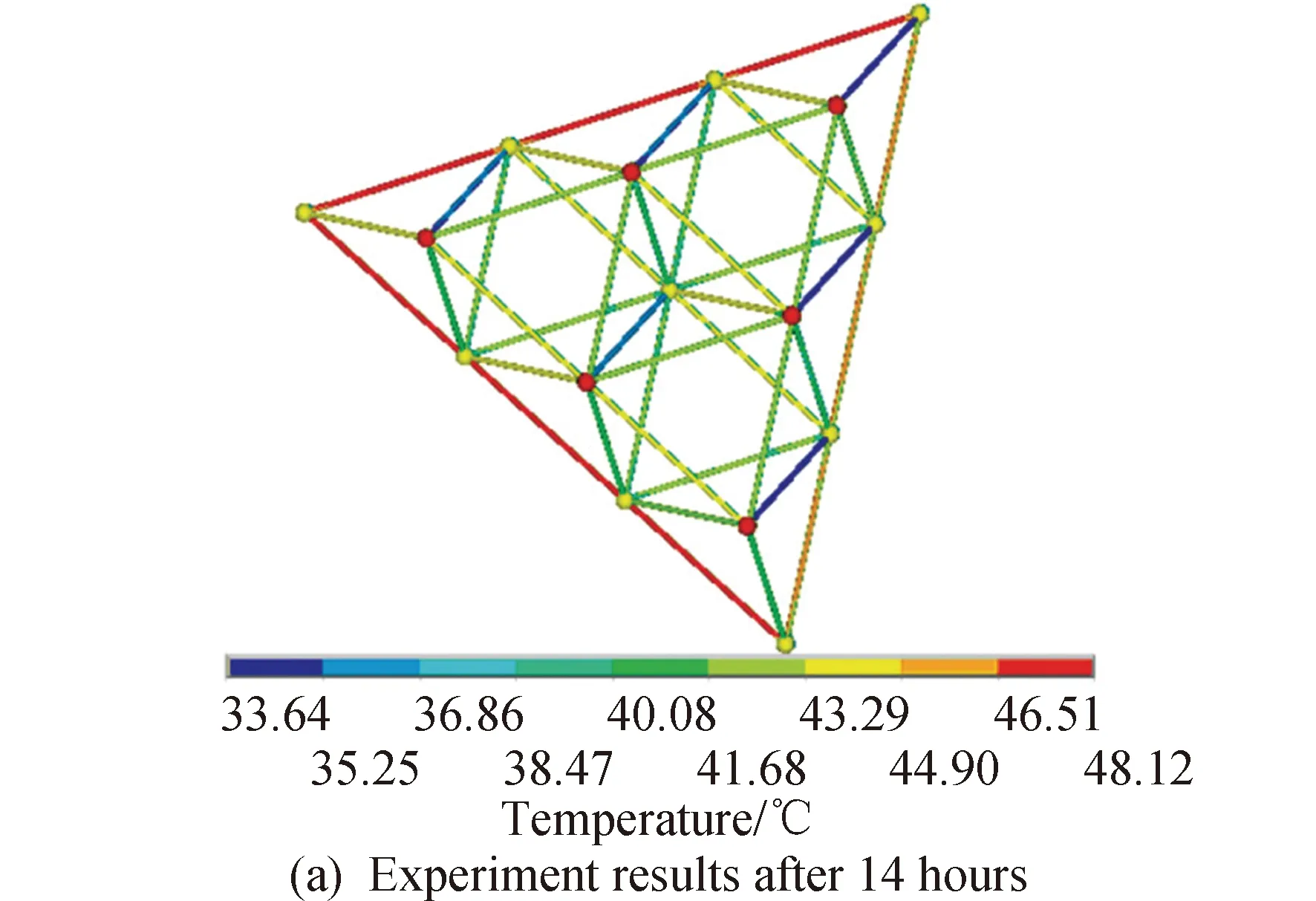
图12 网架结构温度场分布比较Fig.12 Comparison of temperature field distribution of grid structure

3 瞬态热分析

3.1 边界条件及基本假设

模块化空间天线支撑桁架结构在轨工作时受太阳辐射形成的瞬态温度场作用，其辐射边界条件假设为[31-32]：

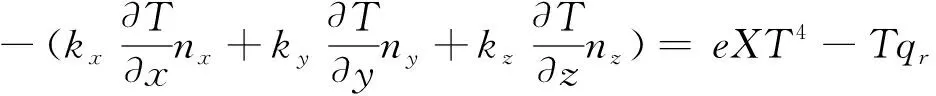
(1)

初始条件为：

T(x，y，z，t=0)=T0

(2)

式中：kx、ky、kz为杆件三个方向的导热系数；X为黑度系数；e为斯蒂芬彼尔兹曼常数；T为节点温度。

本文研究瞬态热分析过程，为简化结构热分析模型，采用如下基本假设：

1)天线支撑桁架结构进出阴影区经历时间为1 h，即3 600 s；

2)根据资料统计，卫星在轨服役24 h内的工作环境温度变化在-200～200℃之间[33]，由此可换算3 600 s内热环境下对结构造成的辐射温度变化范围为73.15～473.15 K；

3)天线支撑桁架结构不考虑阴影遮挡，在各个时间段中桁架结构各杆件受到热辐射相同。

对天线支撑结构进出阴影区温度变化进行曲线拟合，可得温度变化函数为：

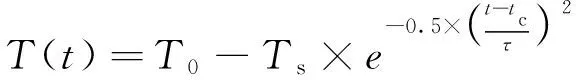
(3)

式中：T0为初始温度；Ts为温度变化幅值；t为时间函数；tc为完全进入阴影区的经历时间，本文取tc=1 800 s；τ为热响应特征时间，本文取τ=440.2 s[34]。

3.2 瞬态热分析

根据以上假设，瞬态热分析中采用link33单元模拟天线结构各弦杆和拉索，将结构杆件和拉索的有效面积赋予link33单元属性，其集中质量采用mass71单元模拟；对19模块空间可展开天线支撑桁架结构的有限元数值模型进行瞬态温度场求解，得到该结构整体在各时刻的瞬态温度曲线，如图13所示。

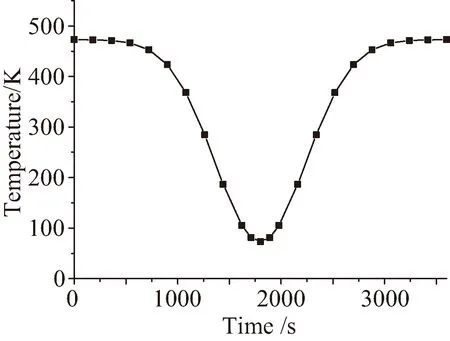
图13 天线结构瞬时温度曲线Fig.13 The instantaneous temperature curve of antenna structure

整个天线结构各杆件在各个时间点的温度相同。取该天线结构在t1=900 s和t2=1 800 s典型累积时间的温度分布情况，此时结构整体温度分别为423.517 K和73.168 K，如图14所示。

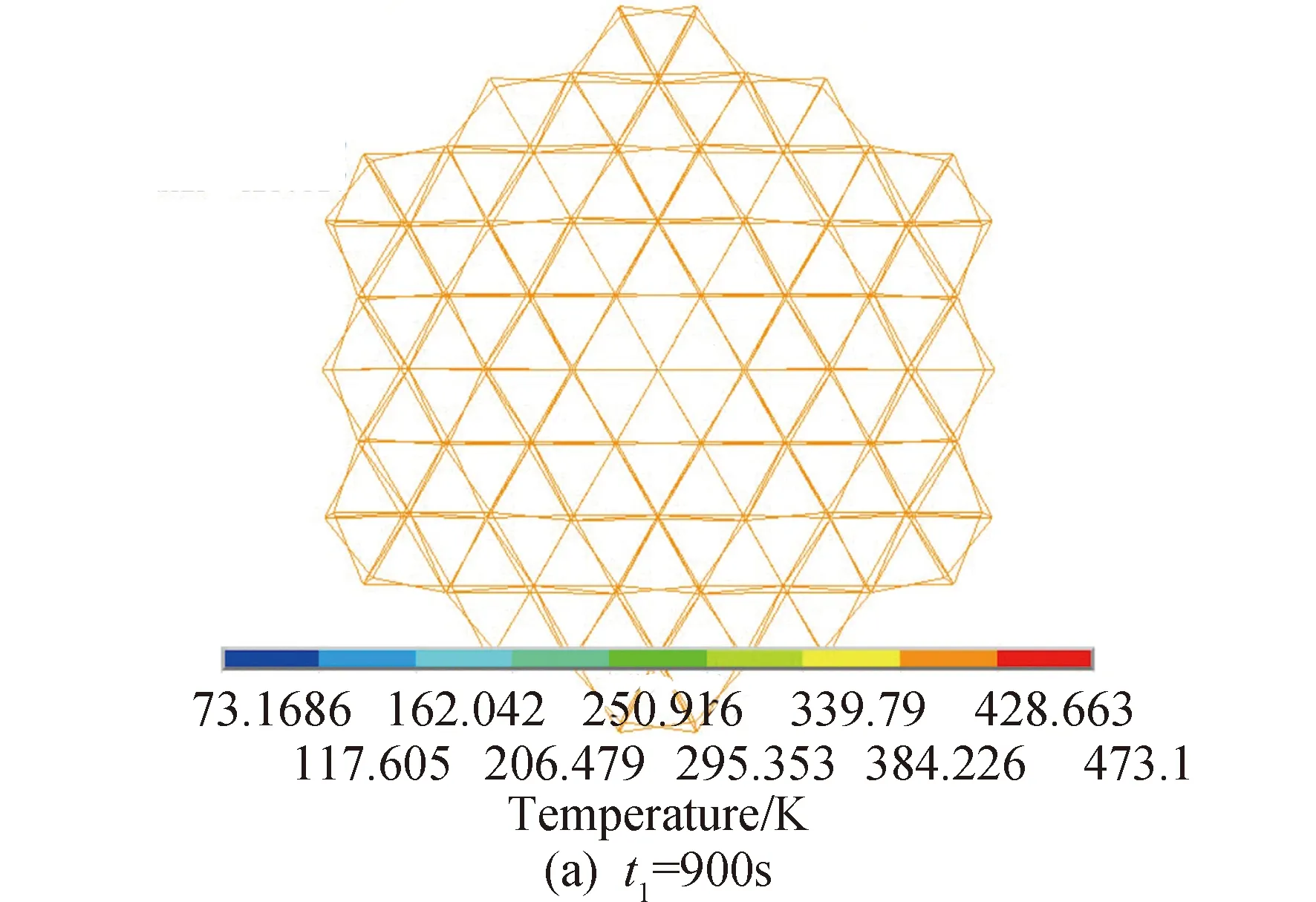
图14 天线结构温度分布情况Fig.14 Temperature distribution of antenna structure

从图13和图14可知，由于未考虑阴影遮挡，天线支撑桁架结构在各时间段中各杆件单元的温度相同，天线结构从初始0 s至900 s进入阴影区过程温度降低缓慢；待天线结构完全进入阴影区时结构温度下降剧烈；1 800 s后天线结构出阴影区过程，天线各弦杆温度与进入阴影区过程变化相反，直至3 600 s后天线结构升温至原温度。上述热分析结果作为热应力分析的求解依据。

4 不同约束位置下的热-结构分析

4.1 模型概况

采用ANSYS APDL有限元软件对结构进行热-结构分析，研究天线支撑结构在瞬态温度作用下的应力发展和位移时程。将3.2节得到的瞬态温度场作为天线支撑桁架结构热-结构分析的温度边界条件，将温度单元link33转化为结构单元link180。由于天线支撑桁架结构在轨工作展开时，其端部与卫星伸展臂连接，将图4中BB′处竖杆处作为天线结构展开支点，施加x，y，z方向的位移约束及绕三轴转动的转角。假设天线桁架结构在温度场作用下材料的热膨胀系数不随温度而变化，且天线结构在初始温度273.15 K下的应力及位移为0，该结构杆件参数见表1。ANSYS建模分析及提取结果均采用国际单位。

4.2 热应力分析

通过间接法进行热分析求解，把求得的瞬态温度场作为体荷载施加在热-结构分析中，得到天线支撑桁架结构弦杆和拉索的最大热应力变化及结构中心点处和边缘处的变形趋势，统计见表3。从表3可知，热-结构分析各时刻结构弦杆的最大正应力发生在第12个模块位置处，最小应力发生在约束处，拉索的最大应力发生在第一圈中间模块。天线结构最大累计变形发生在第16模块且距离约束(BB′)最远端处，变形在32.05～-39.02 mm范围内，上层中心点处变形在13.15～-15.91 mm范围内。由此可见，天线结构中心点处热致变形对天线形面精度的影响不可忽略。结构的变形和应力变化与瞬态温度场曲线一致，在1 s和3 600 s时，结构的弦杆最大正应力均为50.67 MPa，拉索最大正应力均为47.94 MPa，结构最大膨胀变形均为32.05 mm；天线结构在1 260 s和2 340 s，即温度为293.15 K时，结构变形和应力非常微小；在1 800 s时，第12个模块位置处的弦杆最大负应力为-61.92 MPa。参照文献[35]中2A12铝合金材料实测压缩屈服强度为fy=384.6 MPa，判断该时刻弦杆材料未屈服。同时从结构整体变形结果看，该杆件中点侧向变形仅为0.7 mm，且应力小于该杆件压缩临界屈曲应力78.69 MPa，此时承受最大应力杆件未屈曲。中心模块(第1圈)拉索位置处最大负应力为-58.84 MPa，此时冷缩变形为-39.02 mm。而在约束BB′处，该竖杆热应力变化极小，与其他杆件相比可忽略。各个时刻下结构第12个模块位置处弦杆的最大应力比中心模块拉索应力平均值大5.23%左右，说明天线结构在瞬态温度场下，弦杆比拉索受到更大的应力。

表3 热应力和变形统计结果

取瞬态温度场t1=900 s和t2=1 800 s时间为例，对天线结构的热致应力分布和整体变形情况进行分析。天线结构各模块热应力分布情况见图15，由图15可以看出，在任何时刻下，天线结构各模块应力分布趋势基本相同。在第一圈中心模块中，拉索应力最大，下弦杆应力次之，上弦杆应力最小；在第二圈模块中，以第6模块为例，其拉索应力最大，上弦杆应力次之，下弦杆应力最小；在第三圈模块中，以第16模块为例，其上弦杆应力最大，下弦杆应力次之，拉索应力最小。同时，也可以看出随着圈数的增加，上弦杆应力逐渐增大，拉索应力逐渐减小。

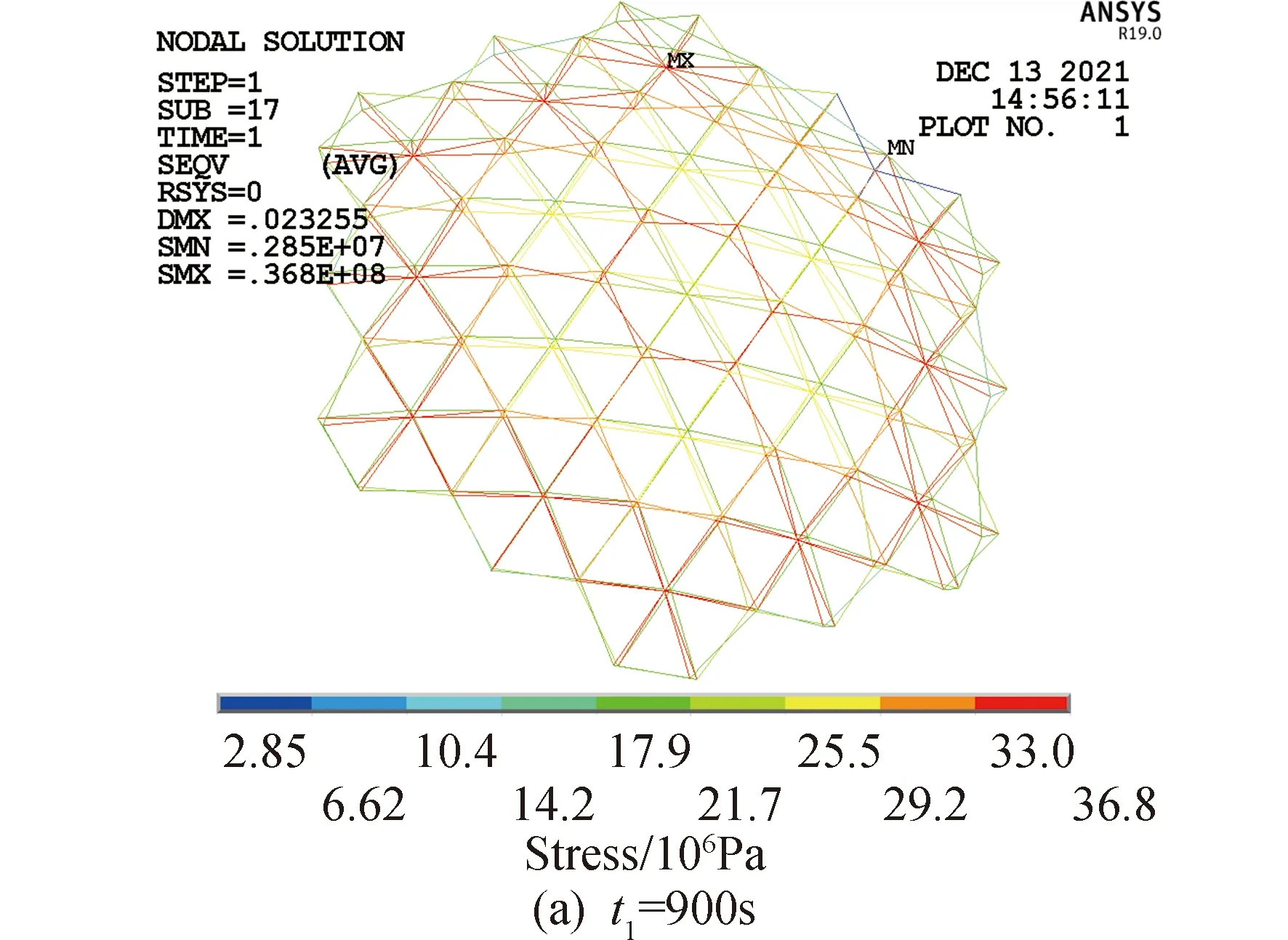
图15 热应力分布Fig.15 Structural thermal stress distribution

为了进一步说明结构各杆件的应力发展，分别提取各圈中第1、6、16模块的上、下弦杆和拉索应力进行比较，见图16各模块杆件热应力分布柱状图。由图16可知，天线结构第一圈模块中上弦杆热应力比下弦杆小8.87%；在第二圈模块中，上弦杆热应力比下弦杆超出17.3%。前两圈模块拉索热应力均为最大，第一圈模块中上弦杆热应力比下弦杆小，第二圈模块中上弦杆热应力比下弦杆大，而在第三圈模块中拉索受到的热应力最小，并且上弦杆最大热应力比拉索大52.27%左右。从图16中还可以发现，天线结构在三圈模块中，与第一圈模块相比，上弦杆受到的热应力逐渐增大7.72%和33.22%，而下弦杆受到的热应力逐渐减小22.43%和24.97%；与第三圈模块相比，拉索受到的热应力逐渐增大46.58%和51.42%。验证并说明天线结构的弦杆在双层抛物面上弦杆受到热应力比下弦杆大，且逐圈递增，拉索与之相反，逐圈递减。

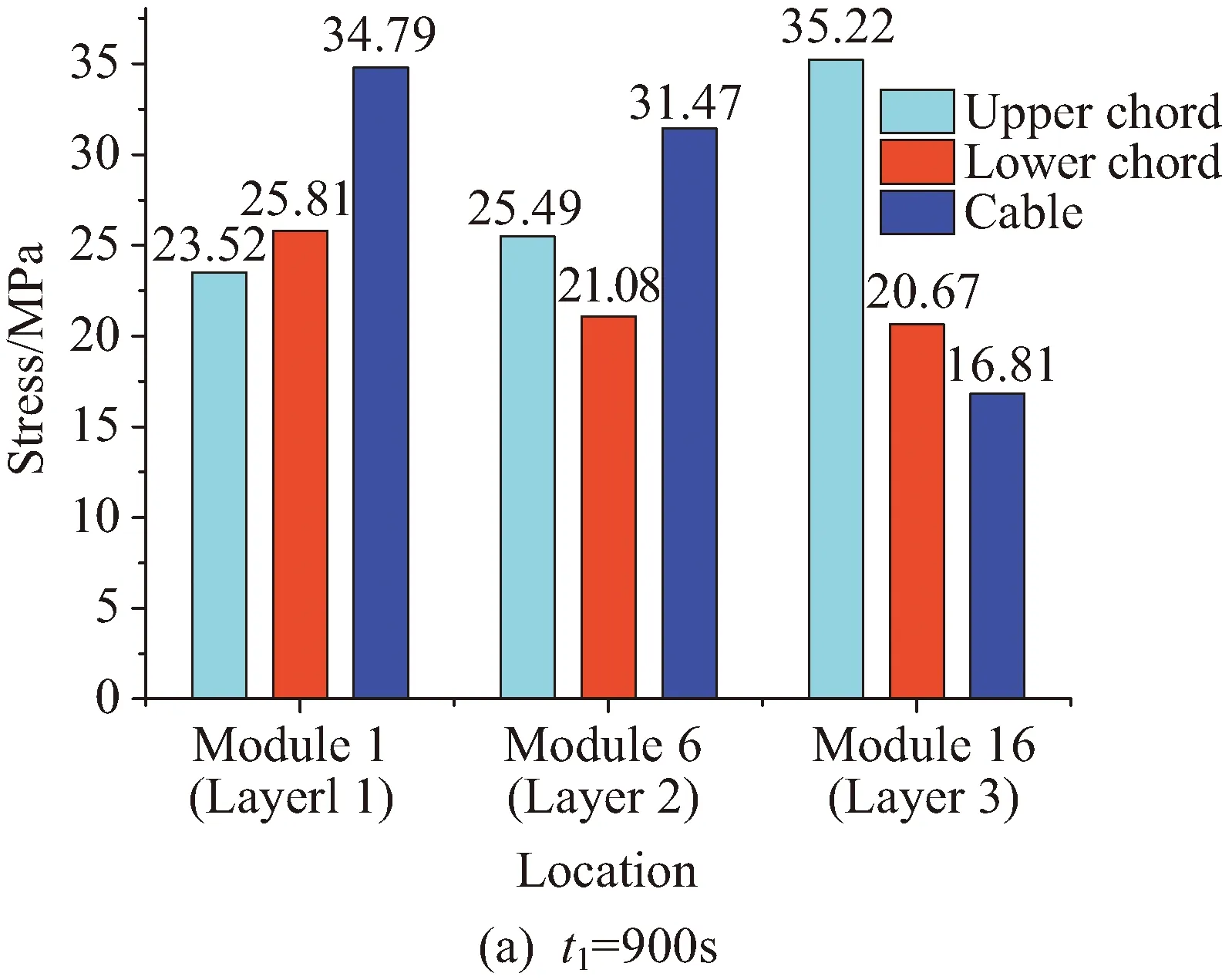
图16 结构各模块杆件热应力分布柱状图Fig.16 Bar chart of thermal stress of each module rod

统计天线结构各构件的热应力极值时间历程见图17所示，其中弦杆的最大应力出现在第12个模块位置处，拉索的最大应力发生在中心模块位置处，最小应力发生在约束处。从图17中可以看出，在任何时刻下，约束处(BB′)的热应力最小；天线结构的极值应力随着进出阴影区，与时间历程瞬态温度场发展趋势基本一致，当进入阴影区900 s左右时，弦杆应力减小27.45%，拉索应力减小27.43%，降低程度基本相同；当进入阴影区1 800 s时刻，天线结构弦杆和拉索都达到最大负应力，1 800 s之后结构应力变化与前1 800 s相反，直至完全出阴影区。

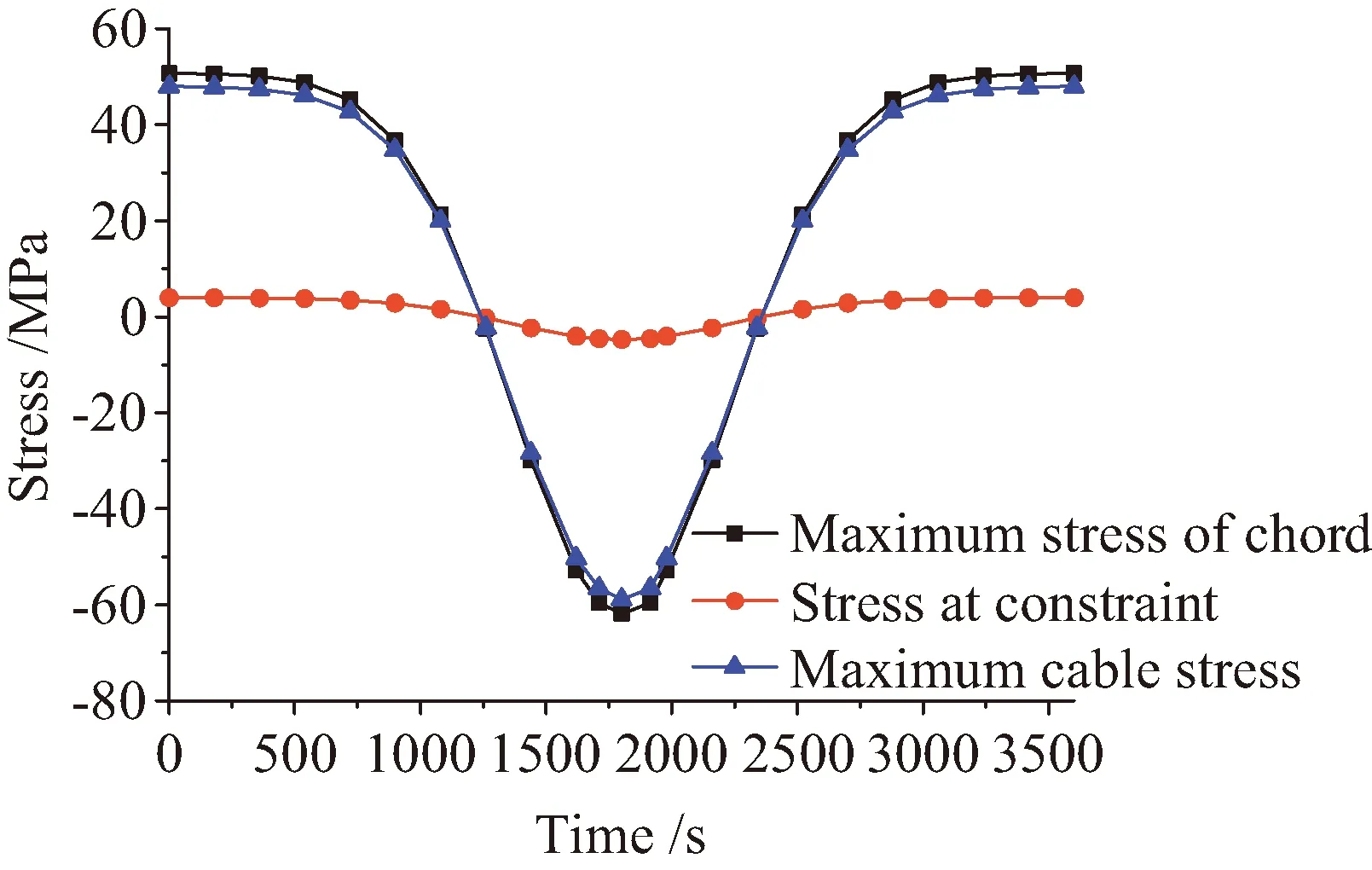
图17 热应力极值时间历程曲线Fig.17 Time history curve of extreme thermal stress

天线结构约束位置处、上层中心点位置以及距离约束最远端位置处随时间变化的曲线如图18所示。由图18可知，在0 s到1 260 s、2 360 s到3 600 s时间段中结构处于热胀伸长阶段，在1 260 s到2 360 s中间阶段结构为冷缩变形。结构在约束竖杆BB′处几乎无变形。距离约束最远端位置处与结构上层中心点位置处变形随时间变化趋势一致，但距离约束最远端位置处的累计变形最大，上层中心点位置处变形幅度在13.15～-15.91 mm之间，针对此变化可进一步研究对天线形面精度的影响。

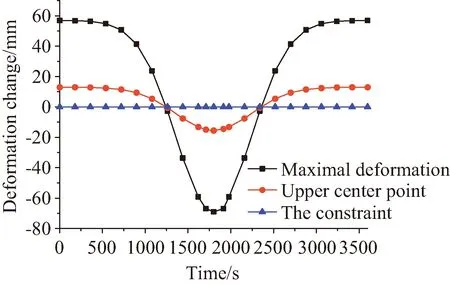
图18 天线结构关键点位置处变形时程曲线Fig.18 Deformation time history curve at key points of antenna structure

取t1=900 s和t2=1 800 s典型累积时间下结构整体变形情况如图19所示，由图可知，在某一时刻距离约束越远，结构在该点的累积总变形越大，天线结构最大变形发生在距约束最远端处。

“我上一次到访查谟-克什米尔大君的斯里那加宫殿时，他们端出了三十个盘子，如果我说任何一个盘子上的宝石都能在市场卖得到一百万元，恐怕是远远低估了这些宝物的美及它所代表的财富。”

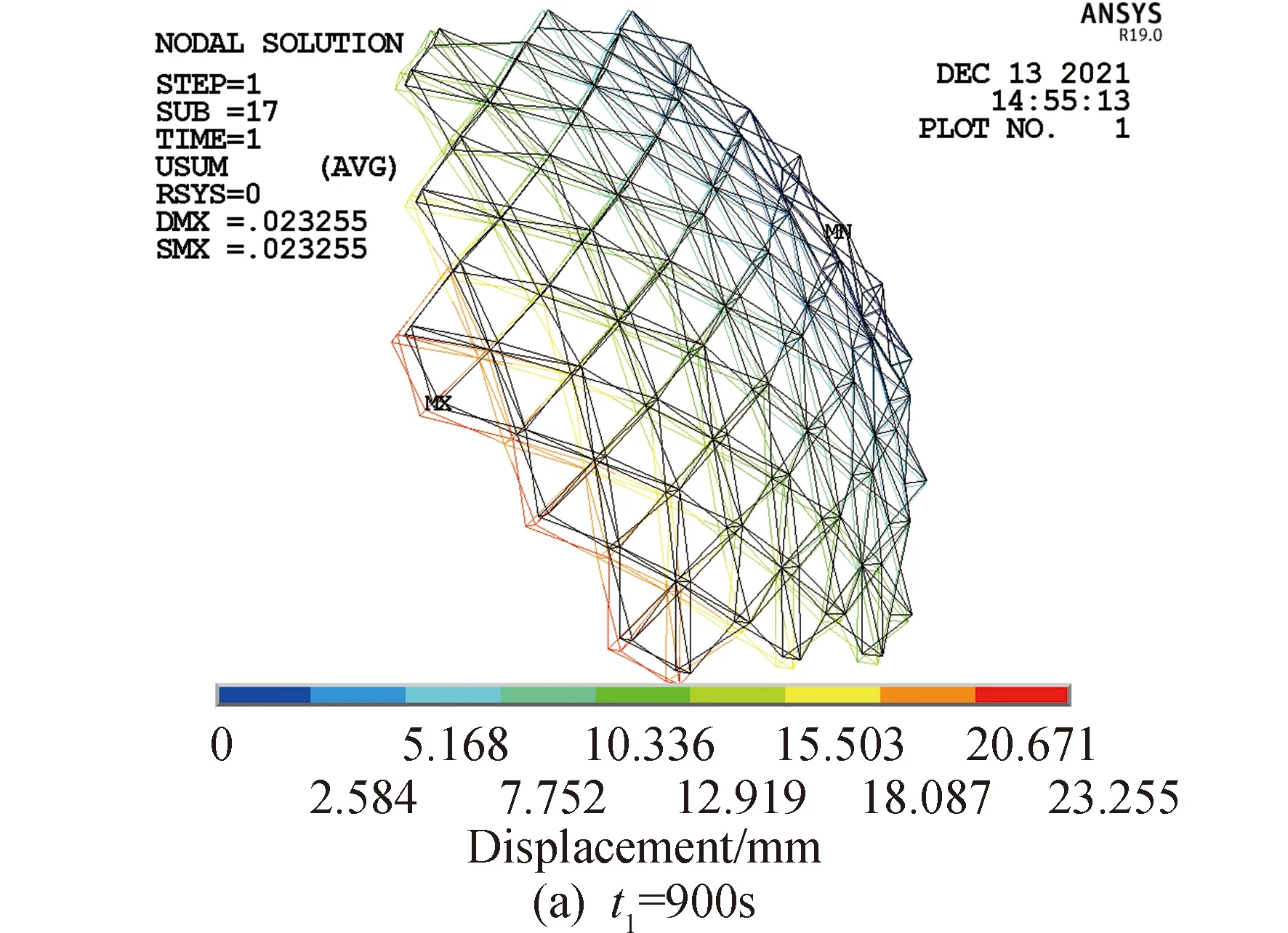
图19 天线结构典型时刻整体变形情况Fig.19 Overall deformation of structure at typical time

通过以上分析可知，瞬态温度场下的天线结构在第一圈模块拉索的作用下，上、下弦杆受到应力变化不大，第二圈到第三圈模块中由于抛物面内侧拉索使天线结构在热交变作用下，上弦杆张紧程度比下弦杆更甚，从而受到更大的应力，并在第三圈模块中达到最值。因此，天线结构在距离约束最远端位置处和结构上层中心点位置处变形，对天线结构形面精度的影响不可忽视。

4.3 不同约束位置下的热致变形

为了进一步分析天线结构受到瞬态交变温度场作用下结构热致变形的影响，分别取天线结构第10、11模块AA′、BB′和CC′竖杆处作为天线展开支点，分析不同约束位置对天线支撑桁架结构变形的影响。当约束设置在上述3个竖杆展开点时，天线支撑桁架结构在t1=900 s后整体变形见图20，在经历t1=900 s、t2=1 800 s、t3=2 160 s和t4=3 600 s时间后不同约束位置下随温度时程的最大变形发展见表4和图21，结构上层中心点处变形发展见表5和图22。

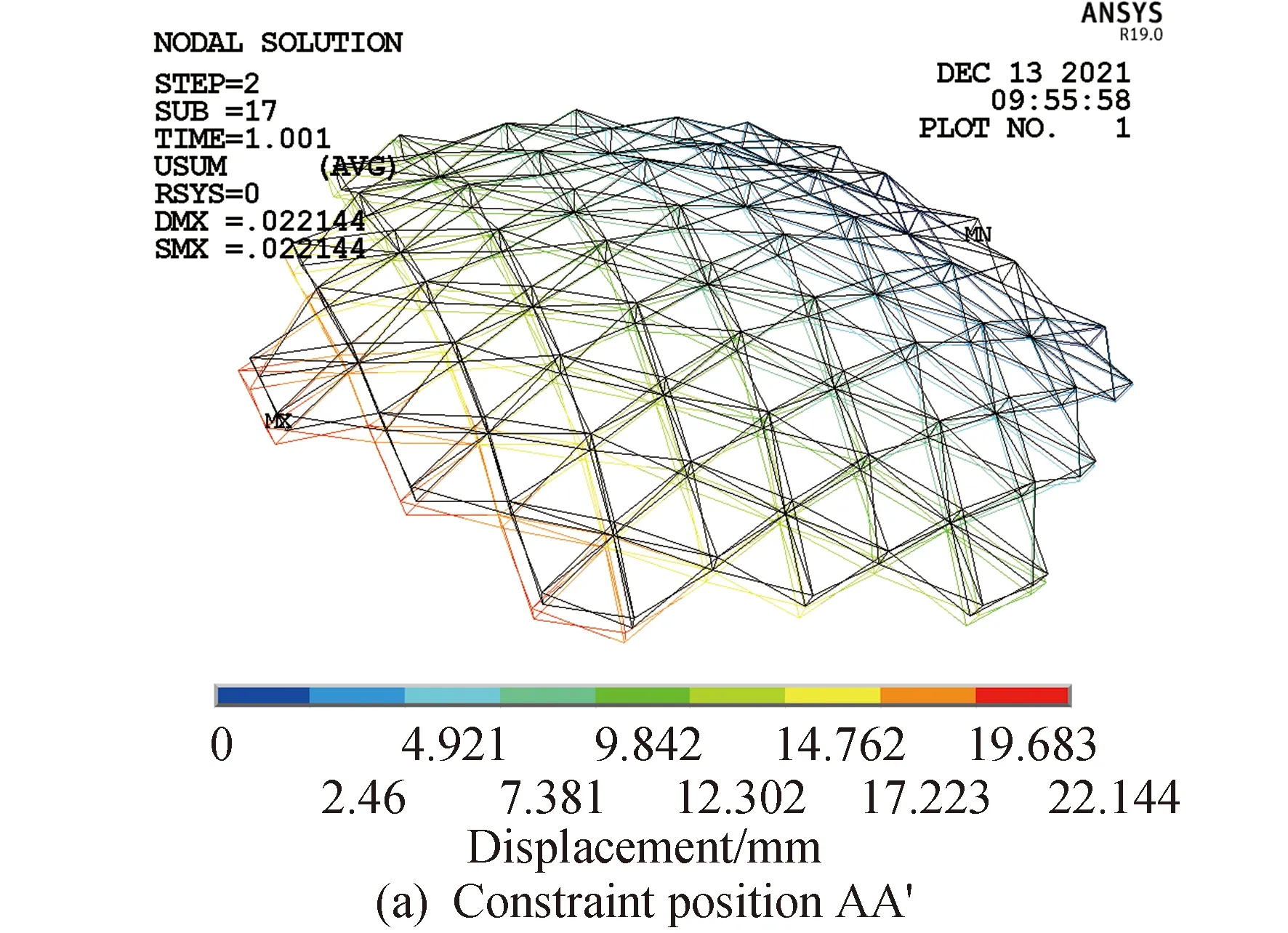
图20 不同约束位置下挠度变形Fig.20 Deflection deformation diagram under different constraint positions

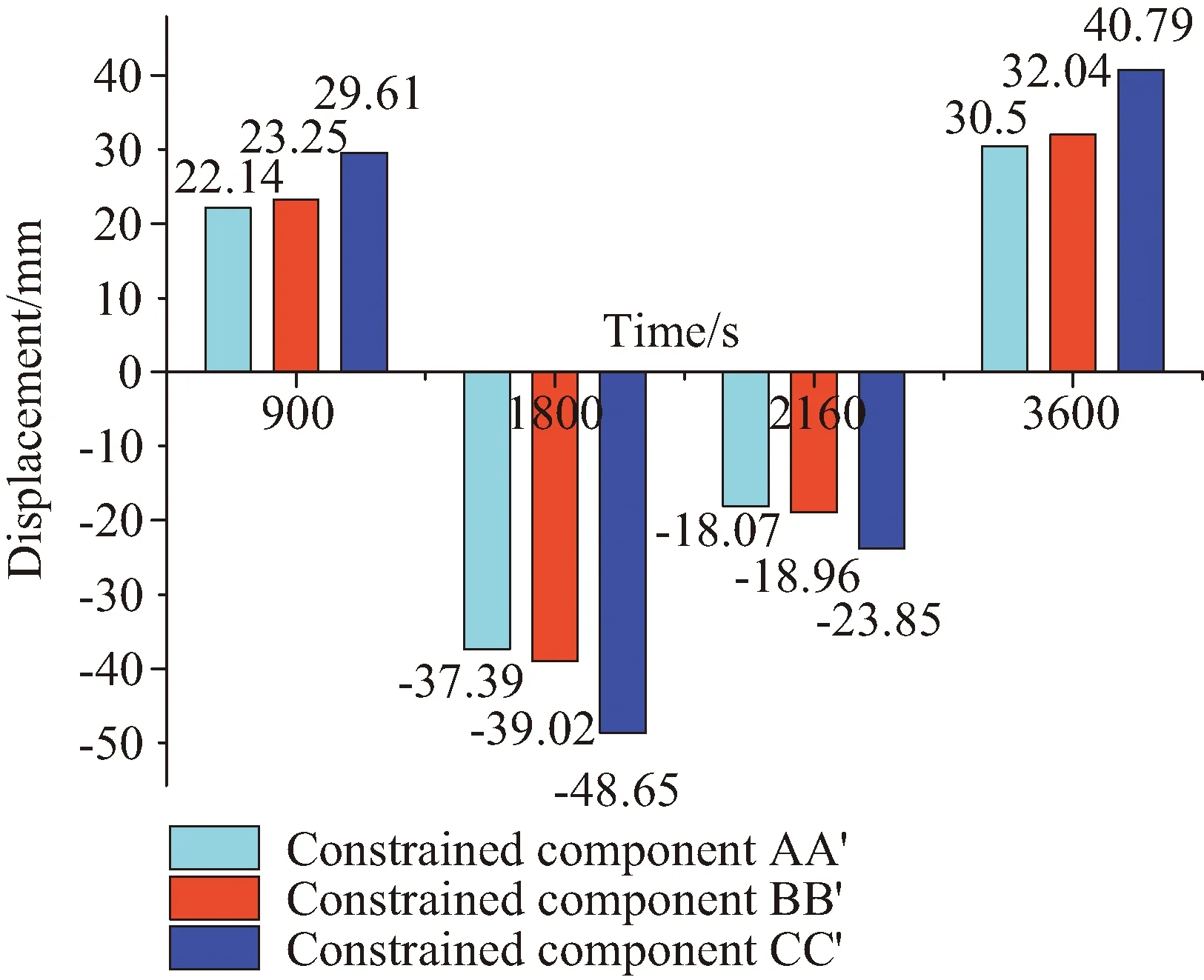
图21 不同约束位置下结构的最大变形柱状图Fig.21 The maximum displacement histogram of structure under different constraint positions

表5 不同约束位置下结构上层中心点处变形

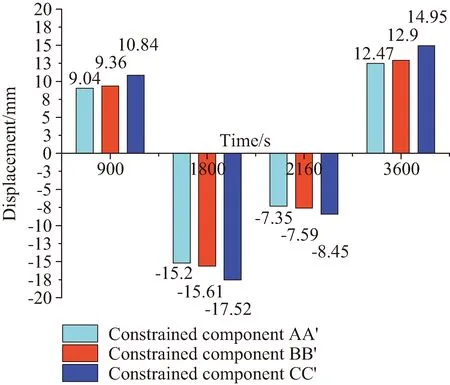
图22 不同约束位置下结构上层中心点处变形柱状图Fig.22 Displacement histogram at upper center point of structure under different constraint positions

从图20可以看出，在t1时刻天线结构在不同约束位置的变形情况。当约束位置在第CC′竖杆处，结构整体变形最大；约束位置在BB′竖杆处，结构整体变形稍小；约束在AA′竖杆时，结构整体变形最小。从表4和图21可知，在经历了t1、t2、t3和t4后，天线结构约束位置在AA′竖杆处，与在CC′竖杆处相比结构整体最大变形减小约33.74%，与约束在BB′竖杆相比结构最大变形仅减小约5.01%。

图22显示了不同约束位置天线结构上层中心点处变形趋势。当天线结构的约束位置在CC′竖杆处，结构上层中心点处变形最大；约束位置在BB′竖杆处，上层中心点处变形稍小；在AA′竖杆处约束其变形最小。由表5对比可知，约束位置在AA′竖杆处与约束位置在CC′和BB′竖杆处相比，结构上层中心点处变形分别减小约16.61%和3.42%。

通过以上分析，天线支撑桁架结构的约束位置选择在最外侧且距离结构中心最近模块顶角和与相邻模块竖杆拼接处，将此位置全约束作为天线结构展开点与卫星伸展臂连接，此时天线结构在瞬态温度作用下结构上层中心点处和整体变形发展可以控制在较小的范围内，从而减弱热致变形导致模块化空间可展开天线网面构型精度下降等不利影响。