考虑安装误差的螺旋锥齿轮啮合性能分析
2022-11-21阿达依谢尔亚孜旦
韩 鹏,阿达依·谢尔亚孜旦
(新疆大学机械学院,新疆 乌鲁木齐 830047)
1 引言
与直齿锥齿轮相比,螺旋锥齿轮啮合时会增加轮齿间的重叠作用。因此,运动传递将比直齿锥齿轮或斜齿锥齿轮更平顺,从而使它们在高速转动下有效的降低了噪声和振动。同时其具有负载能力高、传动效率高等优点,被广泛应用于汽车、飞机、机床等机械中。其噪声,振动和耐久性的水平通常主要受接触方式以及传输误差的影响。在传动过程中产生误差的因素包括螺旋锥齿轮的准共轭特性、变形、制造误差、安装误差等。它们对螺旋锥齿轮传动动态性能、齿面接触质量和振动噪声有着较为重要的影响。而安装误差则是人为的一种不可避免的影响因素,它会直接改变轮齿的接触方式,并对齿轮的传递性能产生影响。最早,文献[1]率先研究了考虑轴承的螺旋锥齿轮啮合接触的几何算法和仿真生成,提出了一种称为“局部综合”的方法,并设计提供了一种预先设计的存在极限传递误差的抛物线函数[2],该函数可控制由安装误差引起的传动误差的线性函数,降低振动等级,达到消除因安装误差引起的传动误差,减小传动时的冲击、振动和噪声等效果。这一方法作为研究螺旋锥齿轮传动误差和啮合性能的基础理论方法。随后格里森公司提出轮齿接触分析(TCA)[3],对局部接触的两齿面的啮合和接触进行模拟,通过轮齿接触分析确定齿面的接触迹线、由安装误差引起的传动误差和由瞬时接触椭圆构成的接触痕迹,在计算机上预先模拟出齿面接触区域的形状、大小和位置,并且可以得到合理的修正参数,进而用这些使齿面接触区域合理的机床调整参数来指导齿轮的加工生产过程,从而有效缩短弧齿锥齿轮的生产周期。在(Tooth Contact Analysis,TCA)理论的基础上,研究学者又提出了齿面加载接触分析理论(Load Tooth Contact Analysis,LTCA)[4],轮齿接触有限元分析(Tooth Contact Finite Element Analysis,TCFEA)方法[5],以及存在安装误差的齿面接触分析(Error Tooth Contact Analysis,ETCA)方法[6]。
近年来,齿轮研究者主要关注的是无边缘接触、无集中应力、传动误差合理等,具备高接触性能的螺旋锥齿轮。因此优化更为合理的啮合区,从而提高螺旋锥齿轮啮合性能成了现今学者们研究螺旋锥齿轮传动的主要研究方向。这里充分考虑安装误差的四种存在形式,通过建立存在安装误差的螺旋锥齿轮三维模型,利用有限元软件进行分析,并分别得到静力学和动力学两种条件下的齿轮啮合性能。通过对比并最终得到了安装误差以及荷载大小对齿轮啮合性能的综合影响。
2 建立齿轮模型
2.1 齿轮三维模型的建立
理想锥齿轮副的基本几何结构是由de1和de2两个节锥相互滚动而成,其锥尖在轴的公共交点处重合[7]。当两个节锥互相滚动时,齿面上的任何一个啮合点都会在球面上移动,球面的中心点与两个节锥的锥尖点重合,如图1(a)所示。齿形的参考轮廓定义在两个节锥之间相切位置的锥齿轮副上,如图1(b)所示。在两个锥齿轮啮合期间,两个齿面之间的啮合点在其上移动,啮合点的运动轨迹即所谓的球面渐开线[8],且在啮合点的任何啮合位置,齿面彼此垂直,从而导致从主动轮到从动轮的连续运动传输。

图1 螺旋锥齿轮建模原理Fig.1 Modeling Principle of Spiral Bevel Gear
这里通过球面渐开线齿廓原理,从渐开线的几何轨迹出发,结合齿轮加工原理,可以确定球面上的齿面几何轮廓。随后利用Matlab语言求解得到齿面各离散点并导入三维建模软件UG中,从而建立参数的螺旋锥齿轮几何模型,如表1所示。
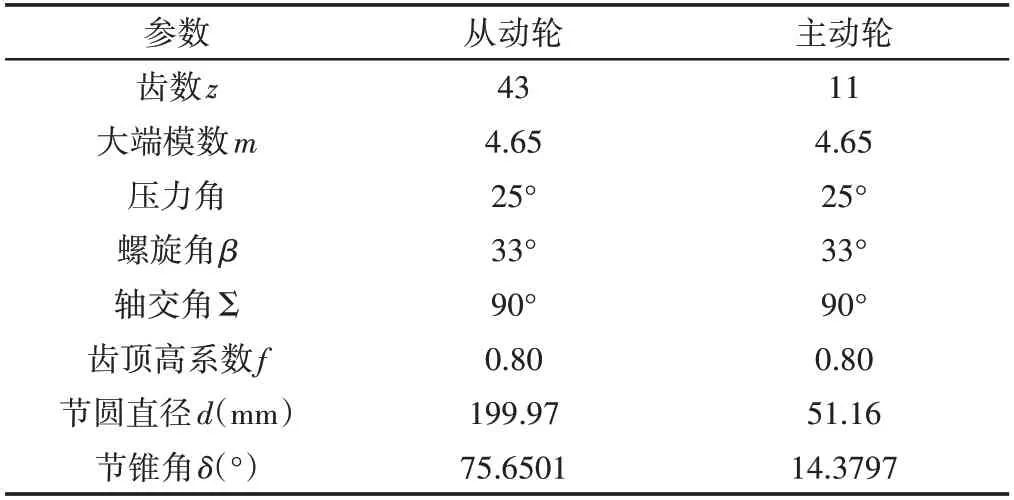
表1 齿轮加工参数Tab.1 Gear Processing Parameters
为简化后续的有限元计算,对大齿轮进行切割。最终确立的螺旋锥齿轮三维模型,如图2所示。

图2 齿轮模型Fig.2 Gear Model
2.2 考虑安装误差的齿轮模型
2.2.1 常见安装误差类型
存在安装误差情况下的螺旋锥齿轮会影响螺旋锥齿轮的啮合质量、振动噪声、齿面接触方式等。安装误差的存在形式主要有四种[9],如图3所示。存在轴间距偏置误差ΔP,如图3(a)所示。存在大齿轮轴向偏移误差ΔG,如图3(b)所示。存在轴交角偏移误差ΔE,如图3(c)所示。存在小齿轮轴向误差ΔT,如图3(d)所示。实际工程中四组误差可能同时产生,综合作用于齿轮。

图3 螺旋锥齿轮安装误差示意图Fig.3 Installation Error Diagram of Spiral Bevel Gear
2.2.2 考虑安装误差的齿轮啮合方程
安装误差等因素会使齿面接触方式从线接触变为点接触,现在我们对齿面接触点进行分析,通过齿面接触点来确定含安装误差的齿面接触轨迹,从而进行存在安装误差的齿面接触计算[10]。
我们根据螺旋锥齿轮齿面的展成运动,将刀盘切削轨迹方程进行坐标变换所得到齿面方程。我们分别令小轮坐标系为S1、大轮坐标系S2、齿轮刚性固连机架所在坐标系为S3,刀盘位置坐标系为Sqi、与刀盘机床固连的坐标系为Spi,考虑安装误差的坐标系为Se。通过啮合原理,可知刀盘上一点M在坐标系Sq下的位置和方向矢量方程如下:

式中:u和θ—刀盘运动参数。
根据齿轮啮合原理可得齿面啮合方程

将刀盘上一点M根据坐标变换原理将其坐标系转化至齿面坐标系,其方法为:

式中:Mi—各部件进行坐标变换的矩阵。我们通过求解齿面接触点可以得到齿面接触轨迹,初始瞬时接触点满足以下啮合方程:

大小轮齿面方程如下:
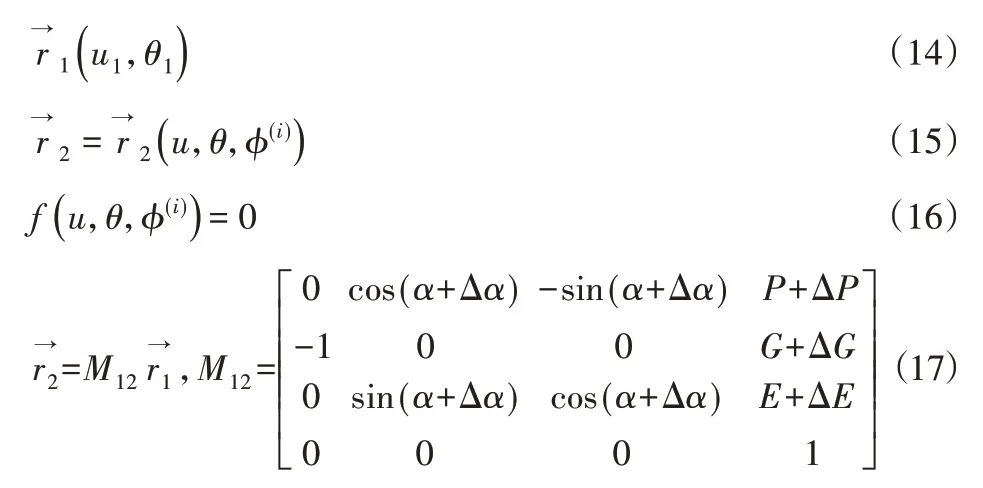
式中:M12—从S1到S2的坐标变换矩阵。
通过考虑安装误差的齿轮啮合方程可以求解得到存在安装误差的螺旋锥齿轮坐标,在前文建立的不含齿轮三维模型的基础上利用UG软件进行坐标调整,最终得到四组存在安装误差的螺旋锥齿轮三维模型。具体安装误差量,如表2所示。

表2 齿轮安装误差偏移量Tab.2 Deviation Value of Gear Installation Error
3 齿轮体网格划分及有限元前处理
3.1 网格划分
螺旋锥齿轮具有空间几何复杂性,使得直接利用ABAQUS等有限元软件生成的齿轮体网格有很大程度上的弯曲变形,降低了网格质量,对有限元分析会产生很大阻碍。所以我们利用有限元前处理软件Hypermesh对齿轮进行网格划分[11]。划分方式,如图4所示。先在一个齿的表面生成如图的壳单元网格,接着在六面体网格划分solid界面的drag操作面板选取网格和特征线,最终完成整个实体的切割。

图4 网格划分示意图Fig.4 Schematic Diagram of Grid Division
3.2 有限元前处理
建立好的有限元网格模型,接下来对齿轮进行有限元前处理工作,如图5所示。

图5 有限元齿轮模型Fig.5 Finite Element Gear Model
(1)设置材料属性,如表3所示。

表3 材料属性Tab.3 Material Properties
(2)建立相互作用及约束:分别选中大齿轮面和小齿轮面作为相互作用面。设置法向接触属性为硬接触,设置切向接触属性的摩擦系数为0.1。接下来分别在大小齿轮轴线上创建一个参考点,并在参考点与齿轮间创建“耦合”约束。
(3)设置分析步:因这里分别对模型做了动态和静态分析,所以分别利用ABAQUS软件的动力学模块和静力学模块创建动力学分析步和静力学分析步。
(4)静态下的边界条件及荷载设置:①固定大齿轮所有约束,对小齿轮施加微小转动量,从而消除轮齿间隙。②对小齿轮仍然施加微小转动量,并释放大齿轮沿轴向的约束,确立齿轮传动接触的初始条件。③对小齿轮施加较大的转动量,使小齿轮足以带动大齿轮,进行正常的齿轮啮合作用。考虑三种工况下的有限元分析结果,故大齿轮分别施加载荷300N·m、500N·m、800N·m。
(5)动态下的边界条件及载荷设置:固定其他自由度,并释放大小轮参考点上沿轴线方向上的旋转自由度,并定义小轮转速20rad/s,大轮所受荷载为500N·m,时间t=0.02s。
(6)输出结果为:大小齿轮的接触应力、大小轮齿根最大应力、大小轮转角。
4 有限元分析
4.1 传输误差的数学模型
齿轮传动误差(Transmission Error,TE)[12]是齿轮系统噪声的主要来源。研究螺旋锥齿轮传动误差,对优化结构设计、降低振动和噪声具有指导意义。螺旋锥齿轮两齿面接触时的第一个接触点的传动比与理论值相等,为随后接触继续进行,接下来的各接触点的传动比与理论值会出现一定的偏差。已知小轮为主动轮,大轮为从动轮,假如传动比始终恒定,大小等于理论值,则当主动轮转角等于θ主时,从动轮的转角大小为θ从=Z2/Z1·θ主。而当传动过程中的各接触点传动比与理论值有一定的偏差时,θ从=Z2/Z1·θ主。此时理论值与实际转角的偏差为可由式(18)表示。

式中:θ主(t)—主动轮(小齿轮)的角度变化;θ从(t)—从动轮(大齿轮)的角度变化;i—两齿轮的传动比,如式(10)所示。

式中:Z1、Z2—大小锥齿轮的齿数。
4.2 传动误差曲线图
4.2.1 静力学传动误差曲线
通过有限元软件输出三种载荷工况下包含四种偏移误差类型的齿轮转角,计算出传动误差值,并绘制出的齿轮传动误差曲线图,如图6~图9所示。

图6 大齿轮轴向偏移Fig.6 Axial Deviation of Large Gear

图8 轴交角偏移Fig.8 Axis Crossing Angle Offset

图9 轴间距偏移Fig.9 Axis Spacing Offset
静态误差曲线分析:
首先可以直观的看出传动误差曲线有较为明显的周期性,此现象是由于当齿轮啮入啮出时所收到的冲击造成的。在较低的荷载运动时,传动误差曲线周期性较为规律[13]。
从图6~图9可以看出,每组模型误差值的大致范围,如表4所示。

表4 误差值范围Tab.4 Error Range
因此可以得到四种误差偏移量的传递误差值从小到大分别是:大齿轮轴向位移、轴间距、轴交角、小齿轮轴向偏移。
(3)传动误差曲线的幅值大小和波动情况可以反映出齿轮的啮合性能。为了更为直观的反映传动误差曲线图的结果,我们通过统计分析方法,利用幅值、平均值以及标准差来衡量比对传动误差曲线结果。
其中,幅值就是一个周期内的最大绝对值,标准差可以反应一组数据的离散情况。我们用传动误差值的标准差对幅值的波动情况进行考量。利用幅值和传动误差的平均值来反映误差曲线值的大小情况,如表5~表8所示。
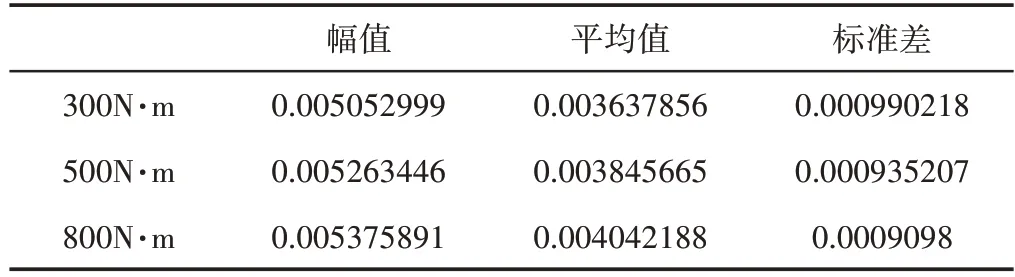
表5 大齿轮轴向偏移Tab.5 Large Gear Axial Offset

表6 小齿轮轴向偏移Tab.6 Pinion Axial Offset

表7 轴交角偏移Tab.7 Axis Crossing Angle Offset

表8 轴间距偏移Tab.8 Axis Spacing Offset
从表中数值我们可以看出四组模型传动误差的幅值、平均值均会随着载荷的增加而增大,标准差则均随着载荷的增加而减小。这说明随着载荷的增大,传动误差值随之增大,而传动误差幅值的波动则变为平缓。
4.2.2 动力学传动误差曲线
在静态啮合分析中,已经得到载荷大小对啮合结果的影响,因此在动态分析过程中,只考虑均在500N·m荷载作用下进行分析,得到的传动误差曲线结果,如图10所示。

图10 动态传递误差Fig.10 Dynamic Transfer Error
模型一:大齿轮轴向偏移、模型二:小齿轮轴向偏移、模型三:轴交角、模型四:轴间距。
同样地,利用统计分析方法绘制误差分析表格,如表9所示。

表9 动态传递误差分析Tab.9 Dynamic Transfer Error Analysis
从表9中我们可以看出幅值,平均值和均方差从小到大依次均为:大齿轮轴向偏移、轴间距偏移、轴交角偏移、小齿轮轴向偏移。动态的分析结果与静态基本吻合。
而从动态误差传递图中我们还可以看出,初始阶段的幅值波动较大,随后振动逐渐减小,并趋于稳定。造成这一现象的主要原因是动态传动过程中,初始状态下的啮入啮出冲击较为严重,随后齿轮转速达到平稳,这一现象便得以减弱,并逐渐稳定。
5 结论
(1)传动误差的周期性是由于当齿轮啮入啮出时所收到的冲击造成的。在较低的荷载运动时,传动误差曲线周期性较为规律。
(2)静态分析中,载荷的增大使得误差值增大,这直接对传动精度造成影响。但是随着载荷的增大,传动误差幅值波动较为平缓,这有效降低了由振动产生的噪声。
(3)动态分析在初始阶段的幅值较静态有较大波动,随后结果则与静态分析基本吻合。
(4)可以得到四种误差偏移量的传递误差值对啮合性能的影响从小到大分别是:大齿轮轴向位移、轴间距、轴交角、小齿轮轴向偏移。因此当我们在无法控制安装误差的前提下,应尽可能减少齿轮所存在的对啮合性能影响较大的安装误差类型。
