基于图像序列的波浪三维重建算法优化

郑耿忠，宋亚男，徐荣华，黎兆锴，李发义

(广东工业大学 自动化学院，广东 广州 510006)

0 引言

波浪作为海洋中常见的物理现象，能反应出海洋的诸多信息，所以监测和研究波浪具有重要的研究意义和应用价值。其中，立体成像技术提供了廉价又不失准确的大范围的波浪观测，并且从中推断出波浪的实时信息。随着技术的发展，波浪测量的精度越来越高。波浪测量技术也从基于几何约束[1]、到基于双目视觉[2]、到基于神经网络[3]逐步迭代更新。本文使用Pixel2Mesh深度学习网络[4]三维重建波浪，Pixel2Mesh以波浪RGB图像作为输入，使用图卷积神经网络[5](Graph Convolutional Network, GCN)处理输出的三维网格，并逐渐将其形变为对应的波浪表面。一方面，深度学习网络在拥有大量数据后通过训练获得强大的非线性映射能力，另一方面，训练后的网络能以极低的计算代价生成重建波浪表面。然而，仅仅使用Pixel2Mesh不能大量恢复波浪细节，重建的波浪易在波浪边缘出现网格点分布不均匀的情况，或者是一些“洞”(没有匹配特征点)出现在高波浪的背面，或者在没有明显光度特征的区域(如破碎波形成的平坦白顶区域)位置。优化三维重建的结果模型，提高精度可以借助波浪的先验知识。比如波浪的时间连续性，波浪观测往往是一段时间内的连续观测，其以图像序列或视频的方式储存和分析，序列中波浪随时间的起伏必然是连续的。本文在重建和分析波浪时结合这一先验知识，优化重建精度；针对“孔洞”问题，联合传统插值和离散卷积神经网络方式进行深度补全。

1 算法框架设计

波浪三维重建的架构如图1所示，使用Pixel2Mesh三维重建网络重建出波浪序列中连续三帧的波浪三维模型，后续设计连续帧组合模块和深度补全模块进行三维模型优化。Pixel2Mesh是一个端到端的深度学习三维重建网络，结合输入的波浪图像frame逐步迭代推理出精确的波浪模型mesh。本文基于此mesh进行模型的后续优化，由于序列的时间连续性，用下标t-1，t，t+1表示连续的3帧并加权组合，生成相对平滑的波浪表面同时生成投影图projection。投影时，以海平面作为投影平面，归一化波浪高度作为像素值。投影后，将网格表示的三维模型转换为单通道二维图像。然后，进行深度补全，通过反距离加权插值(Inverse Distance Weighted，IDW)粗略补全生成projection’；同时，补全前后的projection相减生成对应的掩膜mask，将mask与projection’维度叠加输入卷积神经网络。卷积神经网络对粗补全过的表面进行优化，同时均匀化了Pixel2Mesh重建表面时分布不均的网格点，恢复波浪细节，如图1所示。

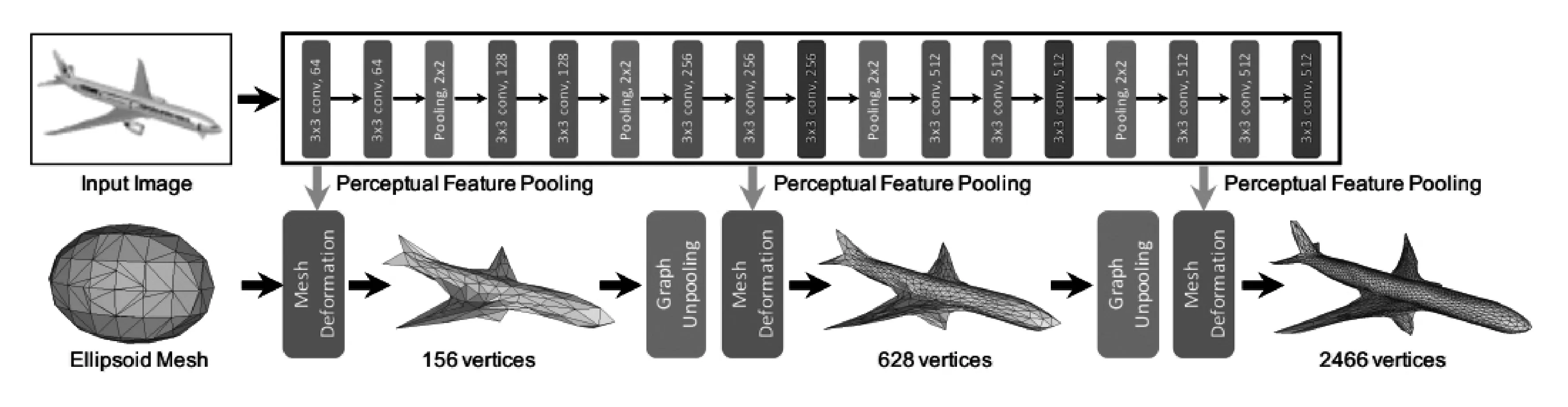
图1 Pixel2mesh网络架构

1.1 连续帧组合模块设计

由于波浪在时间和空间上都是连续的，所以连续(相邻)帧之间的波浪存在时间连续性。如果连续帧间隔时间足够短，可以把两帧中的波浪近似为相同的。由于数据集中波浪图像是定时等间隔拍摄的或是以视频的形式拍摄的，按照这个思想，可以利用连续帧平滑当前帧的波浪：将3帧分别命名为mesht-1，mesht，mesht+1，其中当前帧为mesht，以平滑当前帧为目的，将三维网格投影至平面后得到投影图projection(简称pro，prot为当前帧投影图)，此时当前帧的投影图应该满足等于连续三帧的加权平均，组合公式如下，其中α∈[0,1]是一个加权参数，在实验中α=0.8是一个相对较优的值。

prot+1

(1)

1.2 深度补全模块设计

深度补全模块是使用IDW粗略地补全投影图，IDW又称反距离加权法，是一种传统的图像插值方法，IDW权重ωi公式如下，其中Di为距离，n为邻点总数：

(2)

Di表示离散点(xi,yi)到插值点(x,y)的距离，x、y分别为二维图中的横纵坐标。

(3)

在插值公式中，p表示一点像素值。

(4)

粗略的投影图往往倾向于非常平滑地关闭“孔洞”，而如果使用小窗口的离散卷积神经网络[6]也可以通过训练实现关闭孔洞，但是网络越深，得出的结果越平滑。而如果使用多尺度的网络，又会变得难以训练，所以本文使用两者结合的方式，即保留了网络训练的能力也不会使得补全的表面过于平滑。使用离散卷积神经网络。网络结构见图2(下)深度补全模块。网络输入也可以看做一种扩展维度的操作：将IDW补全后的二维图减去起始投影图pro得到单通道mask，与补全后的二维图一起送入卷积神经网络。其中，原来的“孔洞”在mask中往往为1，而没有改动的地方mask为0或者接近0。网络中，卷积神经网络对稀疏数据进行一系列4次的ReLU激活的稀疏卷积。最后，得到最终的输出波浪曲面。

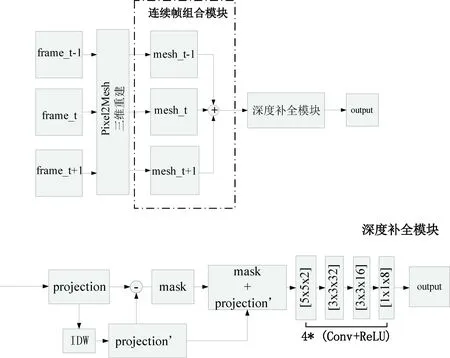
图2 波浪三维重建框架(上)，深度补全模块(下)

2 测试与分析

2.1 数据集

为了验证本文算法的有效性，使用2011年在黑海海洋水文物理研究所研究平台上获得的双目系统记录数据集[7]，该平台位于黑海Katsiveli海岸(44.39°N, 33.98°E)附近500 m的海岸；观测区水深约为30 m；双目相机安装在海面以上11 m，使用一对同步的500万像素(2 048×2 456pixels) BM-500GE JAI相机，焦距5 mm。此次训练设备参数如下：基于Ubuntu16.04操作系统，python2.7+Tensorflow1.3.0+cuda8.0环境，CPU为Intel i5-7400，主频率为3.00 GHz，GPU使用NVIDIA GeForce GTX 1050。

2.2 评价指标

由于卷积神经网络最终的输出为二维的波浪高度图，故采用传统的图像质量客观评价方法作为指标。图像质量客观评价方法是根据人眼的视觉系统建立的数学模型，并通过具体的公式计算表达图像间的相似性，在本文中以结果波浪与真值的相似性来评价结果波浪的精度。本文使用两个指标：均方误差(MSE，Mean Squared Error)和峰值信噪比(PSNR，Peak Signal to Noise Rate)。均方误差公式如下，其中m和n为图像的长和宽，i和K分别为做对比的两个图像，该值越小说明图像越接近。

(4)

峰值信噪比是衡量图像失真或是噪声水平的指标。公式(5)中，MAX表示图像像素的最大数值，8bit图像最大值为255。MSE为均方差，该值越大说明图像越接近。

(5)

2.3 实验结果评估

对比Pixel2Mesh三维重建得到的波浪(未经过优化)和经过本文算法优化后的波浪，计算评价指标，验证优化后的波浪更加接近数据集中的真值。如表1—2所示，优化后的波浪的指标更好。与重建精度相比，未经过优化的有所提高。

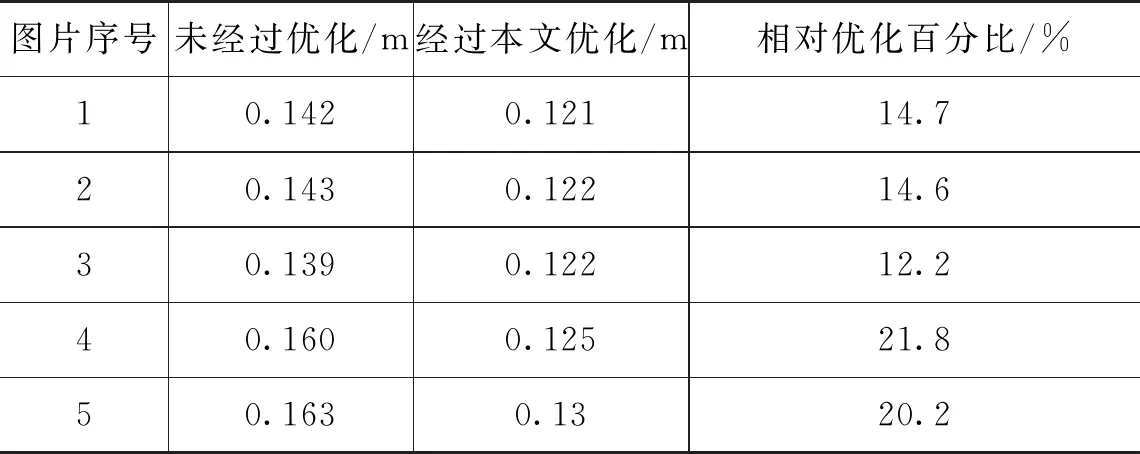
表1 经过优化前后的MAE

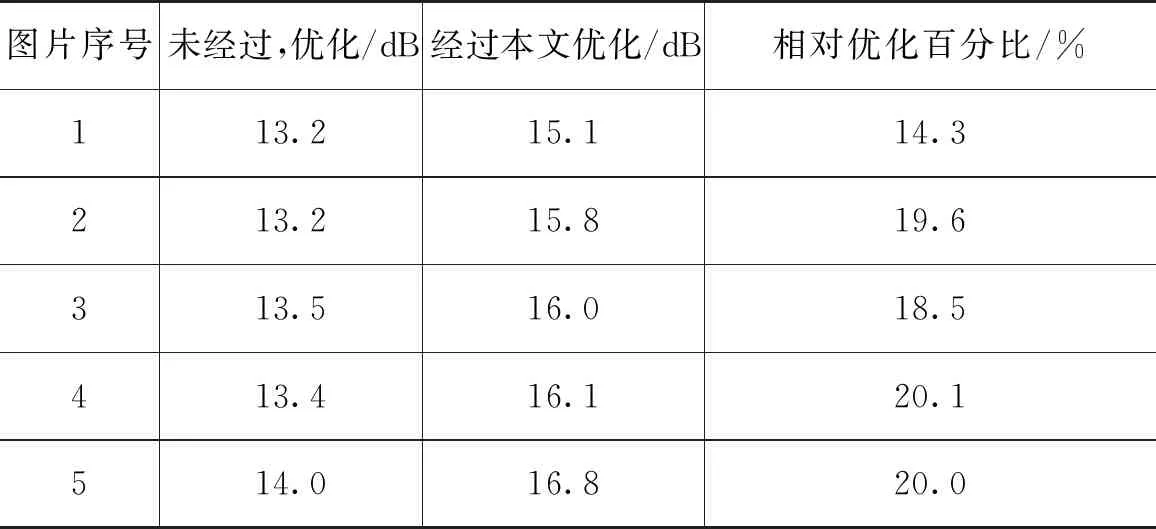
表2 经过优化前后的PSNR

2.4 基于可视化的结果分析

为了对结果进行定性对比，将二维投影图以散点形式绘制出来。其中，点的像素值代表点的高度，像素点越黑表示该点高度越高。图3中左右分别为重建后未优化、重建后优化的散点图。从图3可以看出，优化后的散点更加均匀。每一行显示了一个场景，第一行中间部分的散点经过优化后分布更加均匀；第二、三行对于散点造成的“孔洞”(右上部分)也能较好地闭合起来。

图3 波浪三维重建结果定性对比

3 结语

本文研究了基于Pixel2Mesh的波浪三维重建时，后续优化提升精度的步骤。本研究利用波浪序列的连续性特点约束最终的输出波浪。训练后，本算法可以以更高的精度重建波浪，提供波浪测量数据。实验表明，新方法有更好的指标表现，更加接近波浪真实值。