车间生产过程的能量足迹建模与加工参数协同优化
2022-11-21邵文婷王太勇
田 颖 邵文婷 王太勇
天津大学机械工程学院,天津,300350
0 引言
为使制造与生产过程更加环保,曹军华等[1]将绿色工厂作为绿色制造的实施主体,通过合理规划工厂内能量流与物质流的走向,优化工厂设备并将生产资源回收利用,从而减少生产过程对生态环境的影响。
要实现绿色工厂对能量流的监测和控制,需要建立工厂主要用能设备的能耗模型。针对机床的能耗建模,王超等[2]建立了数控机床能耗的状态节点模型,通过功率信息与通信信息判断机床的运行状态,实现对机床能耗的实时监测;PARK等[3]建立了数控机床的加工参数与能耗的关系模型,构建了有置信区间的能耗预测函数;ZHOU等[4]建立了包含工艺参数信息的机床能耗模型,通过比能耗和工件材料去除率来快速预测能耗。在机器人能耗建模方面,MOHAMMED等[5]对机器人进行动力学分析,建立了机器人的空间能耗模型;PARYANTO等[6]分析了机器人运行参数与能耗的关系,建立了机器人的动态能耗模型。综上所述,目前对数控机床设备的能耗建模多以能耗预测为主要目标,重点考虑机床本身工艺特性的影响因素,而对机床加工过程中的环境因素(如刀具的退化对加工能耗的影响)研究不充分,且大部分能耗建模都基于独立的生产设备,对生产系统的多装备能耗建模研究较少。
优化生产车间能耗的方法包括调整设备的工艺参数、改变车间生产调度方案等。对于加工路径和生产节拍确定的生产车间,能耗优化集中在调整设备的工艺参数。在以加工参数为主要对象的能耗优化中,黄拯滔等[7]分析了数控机床系统的功率去向,通过引力搜索算法优化加工参数来减少生产能耗;陈行政等[8]建立了机床不同工作状态的能耗模型,通过改变加工参数来优化机床的生产能耗、生产成本及加工时间;XU等[9]建立了机床能量和刀具磨损状态的关系,通过人工神经网络方法对加工参数进行优化,以减少加工能耗。在对机器人的能耗优化方面,ZHANG等[10]建立了工业机器人的能耗模型,通过蜂群算法优化机器人的路径节点速度,降低了机器人运行过程中的能耗。在以车间生产调度方案为主要对象的能耗优化中,SOBOTTKA等[11]采用遗传算法优化生产过程及生产线布局来减少生产能耗。综上所述,目前的加工参数多目标优化研究多关注优化指标函数及优化算法的选取,但优化对象的单一性导致优化方法多局限于独立设备的单一加工过程,对生产系统整体的参数协同优化研究较少,生产车间的优化多考虑生产布局与生产调度,而不考虑单台设备加工参数的影响。
针对以上不足,本文以自动化生产车间为研究对象,结合刀具退化信息,以及设备的多样性与相互配合需求,研究了典型用能装备机床、机器人等在机加工作业过程中的能量属性转换规律,建立了装备关键工艺参数与输出能耗间的定量流动关系函数即设备能量足迹模型[12]。进而结合车间调度方案获得生产车间总体的能量足迹模型,对车间生产过程汇总能量动态运行规律进行高实时精准描述。将融合工艺参数信息的设备能耗指标、生产成本指标、生产时间等作为动态评价指标,建立了多目标优化函数,借助蚁群算法实现了生产车间内部多设备间的加工参数协同优化。
1 面向节能的生产车间多装备加工参数协同优化
本文以生产设备的加工参数为优化对象,通过建立加工参数、生产数据与能量消耗的关系,实现能耗的优化。优化整体方案流程的框架如图1所示。

图1 生产车间多装备加工参数协同优化流程框架
确定车间各设备的能耗水平,筛选出主要的用能设备。通过传感器采集主要用能设备的生产数据,考察其运行时的能量流动动态特性,建立设备独立加工时的能量足迹模型。结合设备的运行时序关系建立车间的能量足迹模型。
在进行最优加工参数选择时,考虑到加工时的能量利用率,将设备能量足迹模型转化为比能耗模型,建立动态能耗指标函数;考虑刀具的磨损、机器人的运动平稳性对加工质量和成本的影响,建立生产车间的成本指标函数。
对上述指标函数模型进行加权处理,建立多目标优化函数,依据不同的优化侧重点提出两组评价方案。通过生产时间与生产节拍计算加工时间,建立包含加工参数取值范围与加工时间的约束条件,使用蜂群算法[10]对优化函数进行多目标优化,依据优化后参数,将应权重因子分配给机床、机器人等设备,实现多装备加工参数的协同优化。
2 车间生产过程能量足迹建模
2.1 车间生产过程能量足迹分析
机床、机器人是车间的主要用能设备,它们在生产过程中的动态能耗规律对车间总体能耗的影响很大,因此将机床、机器人作为主要研究对象,分析其工作能耗。
机床的加工功率Pmw为与加工参数相关的函数:
Pmw=f(n,f,ap,ae,tT)
(1)
式中,n为主轴转速,r/min;f为进给速度,mm/r;ap为切削深度,mm;ae为切削宽度,mm;tT为该刀具已加工时间,min。
机床的加工时间tm由加工参数与单个工件去除的材料体积V共同决定:
(2)
机床的总能耗Wm由机床功率积分得到:
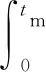
(3)
式中,2tr为上下料总用时;tr为机床的上料时间;ts为机床的待机时间;Pms为机床的待机功率。
机器人的工作功率Prw为与机器人工具中心点(tool center point,TCP)速度有关的函数:
Prw=f(vT)
(4)
式中,vT为机器人的TCP速度,mm/min。
tr由TCP速度vT与机器人工具中心点移动总距离L所决定:
(5)
机器人总能耗Wr为

(6)
式中,Prs为机器人的待机功率。
生产车间主要用能设备的总能耗为
(7)
式中,Wmi为第i台机床的能耗;Wrj为第j台机器人的能耗;Wo为生产车间其他固定能耗;xm为车间中机床的数量;xr为车间中机器人的数量。
2.2 主要用能设备能量足迹建模
本文基于实验数据分析生产车间中机床与机器人的能量流动规律,并对其进行能量足迹建模。首先分析机床切削时的能量足迹。使用FANUC数控铣床TSIM-VMA8050V4直线顺铣45号钢。如图2所示,在相同的切削条件下,刀具磨损大时,主轴切削功率显著增大。因此,要建立准确的机床切削能量足迹模型,就必须综合考虑刀具生命周期磨损规律的影响。

图2 主轴切削功率变化情况
机床主轴的切削能耗与加工参数密切相关,刀具磨损造成的切削能耗上升幅度与加工参数相关。根据广义泰勒公式,建立切削能耗与加工参数及刀具已加工时间tT的关系式:
(8)
式中,K1、K2为与机床、刀具、切削对象等相关的系数;a1~a8为各个加工参数的指数。
机床的总能耗为
Wm=Wmw+Wms
(9)
式中,Wmw为机床的主轴切削能耗;Wms为机床除主轴切削能耗外的其他系统能耗。
机器人的工作能耗与机器人的运动速度密切相关。根据广义泰勒公式建立机器人一次上料的能耗与TCP速度vT的关系式:

(10)
式中,K3为机器人、工件等相关的系数;a9为TCP速度的指数。
机器人的总能耗为
Wr=Wrw+Wrs
(11)
式中,Wrw为机器人的工作能耗;Wrs为机器人的待机能耗。
3 加工参数协同优化
3.1 加工参数优化指标函数
有效的协同优化方案不仅能处理大批量定制生产模式下生产需求的变化,还满足定制生产对产线响应的高效性与批量生产对质量的稳定性的要求。
3.1.1动态能耗指标函数
工业中通常使用比能耗即切削过程的能耗与去除材料体积的比值来表示加工过程中的能量利用率[8]。将机床切削能量足迹模型(式(8))转换,可得到机床切削单个工件的比能耗模型即机床切削的动态指标函数:
(12)
式中,N为刀具所切削的工件的数量。
机床的进给系统、冷却系统、照明系统等其他部分的能量消耗也不可忽略。将加工过程中机床其他部分的功率视为恒定值,则机床加工单个工件的其他系统能耗为
Wms=Pmo(tm+2tr+ts)
(13)
式中,Pmo为机床其他系统总功率。
建立机器人的比能耗模型即机器人工具中心点移动固定距离的能耗(机器人一次运输所消耗的能量),直接将式(10)作为机器人的动态能耗指标函数。
除了工作能耗以外,机器人在待机时间段也有一定的能量消耗,将机器人的待机功率视为恒定值,单个工件加工过程中机器人的待机能耗为
Wrs=Prs(tm+ts)
(14)
式中,Prs为机器人的待机功率。
3.1.2生产成本指标函数
为简化分析,本文中的车间生产成本专指机床及机器人的运行成本。对于无人生产线来说,机床的运行成本以刀具成本为主。
刀具成本Cm由加工单个工件所消耗的刀具个数与刀具的价格得到:
Cm=VHt/T
(15)
T=TVV
(16)
式中,T为刀具在有效寿命内所去除材料的总体积;Ht为单把刀具的价格;TV为刀具在有效寿命内可加工的工件数。
将TV作为刀具寿命的评价指标,则刀具寿命为与加工参数相关的函数为
TV=f(n,f,ap,ae)
(17)
根据广义泰勒公式,建立刀具寿命与加工参数之间的函数:
(18)
式中,K4为与刀具材料、工件材料等相关的系数;a10~a13为加工参数的指数。
机器人运动不平稳会造成物料的损坏、残次品的增加,因此机器人的运行成本以损坏的物料成本为主。物料损坏成本Cr由出现残次品概率与物料的价格得到:
Cr=(1-q)Hp
(19)
式中,q为工件在运输过程中质量合格的概率;Hp为单个工件的价格。
机器人成功运输工件的概率为
q=1-k1/S
(20)
式中,k1为概率系数;S为机器人的运动平稳性指标。
机器人的运动平稳性与机器人在运动过程中的最大功率相关:
S=k2/Pmax
(21)
式中,k2为机器人的平稳性系数;Pmax为机器人一次运输过程中的最大功率。
机器人的最大功率为机器人TCP速度的函数,则根据广义泰勒公式可得

(23)
式中,K5为与机器人、工件等相关的系数;a14为TCP速度的指数。
生产车间的总成本为
C=Cm+Cr
(24)
3.2 多装备加工参数协同多目标优化
3.2.1加工参数协同多目标优化函数
本文的优化目标为生产车间主要用能设备的能耗与生产成本。多目标优化函数采用线性加权求和法。两个优化指标归一化处理后的多目标优化函数为
F=w1Wn+w2Cn
(25)
式中,Wn、Cn分别为归一化后的动态能耗指标函数和生产成本指标函数;w1、w2为优化目标的权重。
3.2.2多目标优化函数的约束条件
为保证设备的正常运行、工件的加工质量、生产任务的准时完成,需对多目标优化函数的优化范围加以约束,约束各设备主要加工参数的取值范围与加工时间,将最终确定的生产车间整体需用时间范围作为多目标优化函数的约束条件。
生产车间的时间模型为
(26)
t=tm+2tr+ts
(27)
机床加工参数的取值范围为
nmin≤n≤nmax
(28)
fmin≤f≤fmax
(29)
apmin≤ap≤apmax
(30)
aemin≤ae≤aemax
(31)
式中,nmax、nmin分别为加工中主轴允许的最大和最小转速;fmax、fmin分别为加工允许的最大和最小进给量;apmax、apmin分别为加工允许的最大和最小切削深度;aemax、aemin分别为加工允许的最大和最小切削宽度。
机器人加工参数的范围为
vTmin≤vT≤vTmax
(32)
式中,vTmax、vTmin分别为加工允许的最大和最小机器人TCP速度。
加工时间的的范围为
(33)
式中,tmax、tmin分别为生产任务允许的单个工件的最长和最短加工时间。
3.2.3基于蜂群算法获取最优参数
为获取最优加工参数方案,本文采用蜂群算法对式(25)进行优化参数求解。蜂群算法优化流程如图3所示。首先初始化种群,依据优化需求确定蜂群总数、优化范围、搜索次数。派出一定数量的侦察蜂在优化范围内进行一次搜索,将搜索到的优化参数代入式(25),得到多目标优化结果,并记录对应的参数值。再派出侦察蜂进行下一轮搜索,对上一轮与新一轮的优化结果采用贪婪选择策略,若新一轮优化结果优于上一轮优化结果,则用新一轮结果的优化参数代替原有优化参数,反之保留原有的优化参数。派出工作蜂,在已记录的优化参数附近随机进行搜索,若搜索到的新优化结果优于原优化结果,则用新优化参数更新原有优化参数,反之保持原有优化参数不变。当工作蜂搜素达到蜜源搜素次数时,评估最优参数,判断是否需要继续搜索。
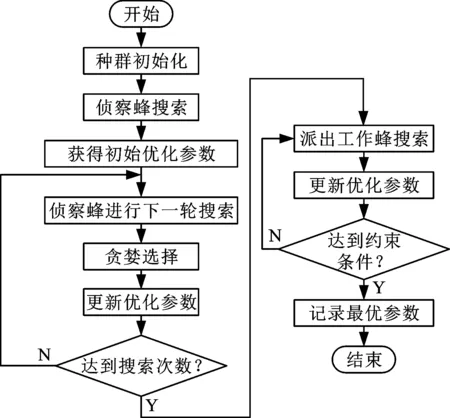
图3 蜂群算法流程
4 实验验证
为验证所提方法的有效性,对图4所示的工件进行加工实验。为实现生产任务,选择图5所示的典型生产车间布局模式。

图4 工件加工尺寸

图5 生产车间装备布局示意图
车间生产节拍给定,各设备的生产节拍与运行时序关系如图6所示,图中,tb为测量仪设备的工作时间,tc为传送带设备的工作时间。
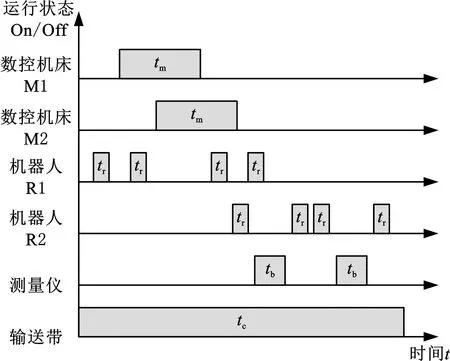
图6 生产节拍与设备运行时序图
依据式(7)可得该生产车间的能量足迹模型:
W=2Wmw+2Wms+8Wrw+2Wrs+2Wbw+Wbs+Wc
(34)
式中,Wbw、Wbs分别为测量仪的工作能耗与待机能耗;Wc为输送带的工作能耗。
依据式(19)、式(24)可得该生产车间的生产成本指标函数:
C=Cm+(1-q2)Hp=Cm+(1+q)Cr
(35)
以生产车间中的机床与机器人为主要优化设备,为确定车间能量足迹模型的具体参数值,使用PW3360-30钳型功率计,通过正交试验获取刀具生命周期的机床切削能耗数据,通过采集不同TCP速度下的机器人功率获取机器人工作能耗数据,以多元线性回归法建立机床切削能量足迹模型与机器人工作能量足迹模型,机床的其他系统功率、机器人的待机功率、非主要优化设备的工作功率与待机功率视为恒定值,从而建立生产车间的动态能耗指标函数。
为确定生产车间的生产成本指标函数,使用XDS-10A高镜身视频显微镜,测量正交试验中四刃铣刀各个刀刃的最大磨损值。4个刃中某一个刃的磨损值满足
(36)

时,判断刀具失效,记录下刀具失效时的切削工件数。
采集不同TCP速度下的机器人最大功率,采用多元线性回归法建立刀具寿命函数与机器人的最大功率函数,再结合3.1.2节内容得到生产车间的成本指标函数。
将动态能耗指标函数、生产成本指标函数代入式(25),建立该工艺流程的加工参数协同多目标优化函数。本文选择能耗权值较大的A组与生产成本权值较大的B组进行优化,权值按照经验给出,如表1所示。为对比优化结果,设置S组为对照组,将其各项加工参数取工业常用参数值,具体数值如表1所示。
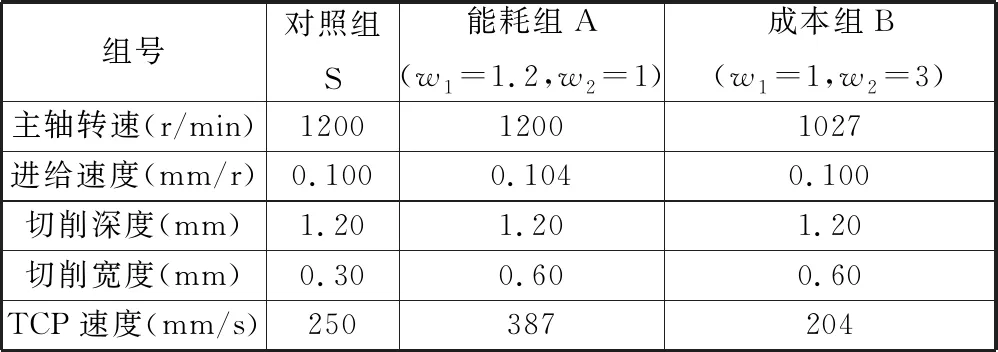
表1 多目标下生产车间多装备加工参数协同优化结果
依据式(26)与生产节拍时序图可得该生产车间加工单个工件的时间:
t=tm+4tr+tb+ts
(37)
依据实验条件与生产任务要求,对多目标优化函数做以下约束:
1000 r/min≤n≤1200 r/min
(38)
0.10 mm/r≤f≤0.12 mm/r
(39)
0.60 mm≤ap≤1.20 mm
(40)
0.30 mm≤ae≤0.60 mm
(41)
200 mm/s≤vT≤400 mm/s
(42)
800 s≤tm+4tr+tb+ts≤1200 s
(43)
取刀具平稳磨损时间段为主要优化时期,通过蜂群算法对上述不同权值的两个多目标优化函数进行优化。选取蜂群包含10只侦察蜂与30只工作蜂。能耗组A的优化过程如图7所示,生产车间各组优化结果如表1所示。

图7 蜂群算法优化过程
使用表1优化后的加工参数加工上述工件,得到图8所示加工单个工件的机床主轴切削能耗对比图,各组优化数据如表2所示。

图8 优化方案的能耗对比图

表2 多目标下生产车间多装备加工参数协同优化数据
优化后的能耗节省率为
(44)
式中,WS为对照组加工一个工件的平均能耗;WA为能耗组加工一个工件的平均能耗。
优化后的刀具寿命延长率为
(45)
式中,TVB为成本组刀具切削工件数;TVS为对照组刀具切削工件数。
优化后的机器人最大功率减少率为
(46)
式中,PS为对照组机器人最大功率;PB为成本组机器人最大功率。
结合式(44)~式(46)可知,相对于对照组S,能耗组A中机床加工一个工件平均节省能耗17.97%,机器人运输工件一次平均节省能耗18.13%,生产时间节省20.66%;成本组B延长单把刀具寿命56.25%,机器人一次运输过程中最大功率减少7.73%,生产时间节省5.99%。
图9为优化结果雷达图,对比各组优化结果可知,A组的机床与机器人整体耗能少,但刀具寿命期内可加工的工件较少。B组刀具寿命期内可加工的工件更多,且机器人运动平稳性更高,但整体能耗高于A组。

图9 优化方案雷达图
5 结论
(1)本文以生产车间为对象,分析了车间主要用能设备的能量足迹,建立了生产车间的能量足迹模型,考虑了刀具退化对设备能耗的影响。
(2)本文以降低车间的生产能耗与生产成本为主要目标,使用蜂群算法优化了车间设备的加工参数。实验证明该优化方式在以能耗为主要优化目标时,机床加工能耗减少17.97%,机器人工作能耗减少18.13%;以成本为主要优化目标时,刀具寿命延长56.25%,机器人运动平稳性增加7.73%。
刀具不同磨损时期的机床设备的最优加工参数也有所不同,应依据刀具不同的磨损时期对优化函数进行分段优化,使得优化算法能够更好地降低加工能耗和生产成本。
