周期性扇形孔结构对斜槽型纵扭复合模态超声振动系统性能的影响*
2022-11-21林基艳林书玉钟兴华
林基艳 林书玉 钟兴华
(1 榆林学院信息工程学院榆林 719000)
(2 陕西师范大学物理学与信息技术学院西安 710119)
(3 长庆油田分公司第二采气厂榆林 719000)
0 引言
近年来,随着功率超声技术的深入发展,传统的一维振动已经很难满足日益复杂的加工要求,能够综合纵向振动和扭转振动优势的二维纵扭复合振动因其较高的加工精度和可靠性而备受青睐[1-2]。目前,很多研究都倾向于采用斜槽结构实现模式转换型纵扭复合振动,该方法实现简单,但能量转换效率低,输出的扭转分量较小,因此,如何从结构上对斜槽型纵扭复合振动进行优化,提高其纵扭转化能力成为迫切需要解决的问题。
文献[3]提出了一种利用在超声变幅杆上加工斜槽的方法来实现纵扭复合振动的超声换能器;文献[4]研究了斜槽的结构参数(个数、宽度、角度等)对纵扭复合振动转换效率的影响,并计算出能使系统获得最大转换效率的最佳斜槽角度和宽度;文献[5]针对斜槽式模态转换型超声电机存在的成本高、工艺复杂的问题进行研究,提出了一种孔式模态转换型超声电机;文献[6]利用单因素实验法,分析了斜槽结构参数对系统振动频率的影响;文献[7]利用灵敏度分析理论,将纵振振幅与扭转振幅的比值作为目标参数进行优化,并获得最佳斜槽型纵扭复合振动超声系统的结构模型;文献[8]通过在喇叭形变幅杆上加工4条均匀斜缝,设计了一种斜缝式纵扭超声振动系统,并采用有限元分析方法对振动系统的机械结构进行了优化,分析了斜缝与纵扭共振频率和振幅的关系;文献[9]设计了一种圆环形斜槽传振杆,并分析了圆环斜槽传振杆的振动特性,求解出能够影响纵扭复合振动性能的因素;文献[10]对单斜槽、双斜槽变幅杆的放大系数进行了计算,并通过仿真分析求解出斜槽参数对不同双斜槽变幅杆放大系数的影响规律;文献[11]利用指数型过渡段的复合型变幅杆,实现了纵扭复合振动,并通过仿真分析,研究了斜槽结构参数对系统共振频率的影响规律;文献[12]通过在中空的阶梯型变幅杆和均匀杆上加工对角线斜缝的方式设计了一种可用于脆性材料孔加工的纵-扭复合振动装置;文献[13]在超声换能器的末端加工4个均匀倾斜的凹槽,将纵向振动转化为纵扭复合振动,设计了一种新型的用于拉丝的夹心式纵-扭复合超声换能器;文献[14]提出了基于梳状扇形孔周期性结构的纵扭复合超声振动系统,但并未具体分析扇形孔结构参数对系统性能的影响规律,也没有给出使系统获得最大的扭转分量的扇形孔结构参数及周期性扇形孔结构的引入对系统性能的改善幅度。基于此,论文提出了周期性扇形孔结构对基于斜槽结构的模式转换型纵扭复合模态超声振动系统性能的影响研究。
1 基于斜槽结构的模式转换型纵扭复合超声振动系统的设计
基于斜槽结构的模式转换型纵扭复合超声振动系统主要分为3个部分:夹心式纵向振动压电陶瓷换能器、圆锥型变幅杆和基于斜槽结构的振动转换体[15-16]。夹心式纵向振动压电陶瓷换能器由前、后盖板,压电陶瓷晶堆3部分组成;变幅杆选择圆锥形;基于斜槽结构的振动转换体则使用加工了4个均匀分布的斜槽的空心圆柱。设计半波长结构的换能器,变幅杆和基于斜槽结构的振动转换体两者共同构成半波长结构。前后盖板和基于斜槽结构的振动转换体都使用Aluminum 6063-T83,杨氏模量6.9×1010Pa,泊松比0.33,密度2700 kg/m3;压电陶瓷晶堆选用Lead Zirconate Titanate(PZT-4),杨氏模量6.45×1010Pa,泊松比0.32,密度7500 kg/m3。基于换能器和变幅杆的设计理论,利用有限元分析法建立系统的模型并初步确定各部分的尺寸,结果如图1所示。图中,基于斜槽结构的振动转换体的内圆半径r1=13 mm,外圆半径r2=17 mm;斜槽的长度为30 mm,宽度为5 mm,深度为2.5 mm,斜槽的角度为10°。
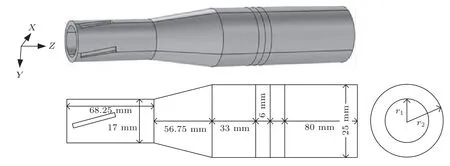
图1 基于斜槽结构的模式转换型纵扭复合超声振动系统的模型和尺寸图Fig.1 Model and size drawing of a mode conversion longitudinal-torsional composite ultrasonic vibration system based on the chute structure
为验证设计的合理性,对系统实施模态分析,搜索5~20 kHz频率范围内的谐振振型,结果如图2所示。
从图2能够看出,当基于斜槽结构的模式转换型纵扭复合超声振动系统的特征频率为12510 Hz、18634 Hz时,纵扭复合超声振动系统以纵振为主;而当特征频率为8036.5 Hz、11436 Hz、17537 Hz时,系统则以扭振为主。以二阶扭振Eigenfrequency=11436 Hz为例进行研究,由图3能够看出,二阶扭振时,基于斜槽结构的振动转换体沿顺时针方向扭转。
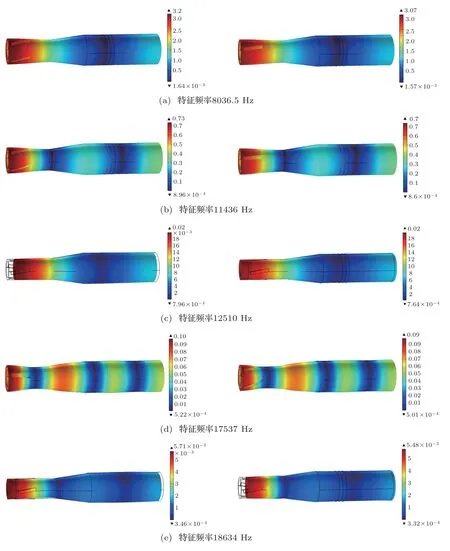
图2 基于斜槽结构的模式转换型纵扭复合超声振动系统的振型图Fig.2 Vibration modal diagram of a mode conversion longitudinal-torsional composite ultrasonic vibration system based on the chute structure

图3 二阶扭振的位移方向Fig.3 Displacement direction of second-order torsional vibration
利用仿真软件求解以二阶扭振为主的基于斜槽结构的纵扭复合超声振动系统的旋转角度、扭转振幅和剪切应力以确定系统的纵、扭振动的转化能力。在基于斜槽结构的振动转换体的输出面上任意选取外圆弧上的一条弧线进行计算,结果如图4所示。因为在小变形情况下,旋转张量的分量可以近似为以弧度给出的角度,而图1建立的系统模型是围绕z轴在xy平面内进行扭转振动,因此,可以利用变形旋转张量的xy分量Rotxy来求解旋转角位移,并将旋转角位移转换为弧度值,即可求出基于斜槽结构的振动转换体的扭转/旋转角度。旋转角度越大,扭转振幅也就越大,证明系统的纵扭转换能力越高,反之,旋转角度越小,扭转振幅也就越小。剪切应力代表基于斜槽结构的振动转换体在单位面积上所承受的剪力,剪应力越大,在同样条件下,能产生的扭矩越大,即系统的扭转分量也就越大。从图4可以看出,基于斜槽结构的模式转换型纵扭复合超声振动系统的旋转角度从2.328°到2.617°,扭转振幅从0.0407 mm变化到0.0461 mm,剪切应力的变化范围从0.206×107N/m2到1.77×107N/m2都较小,为了增大系统的扭转分量,提高纵扭振动的转化能力,需要对基于斜槽结构的模式转换型纵扭复合超声振动系统进行优化。

图4 基于斜槽结构的振动转换体辐射端面的旋转角度、扭转振幅和剪切应力Fig.4 Rotation angle,torsion amplitude and shear stress of the radiation end face of the vibration converter based on the chute structure
2 基于周期性扇形孔和斜槽结构的模式转换型纵扭复合超声振动系统的设计
为了提高基于斜槽结构的模式转换型纵扭复合超声振动系统的扭转分量,在基于斜槽结构的振动转换体的空心圆环内部,加工了4个围绕半径为rx的圆柱周期性分布的扇形片,每个扇形片的中心角都为β,优化后的振动转换体如图5所示。
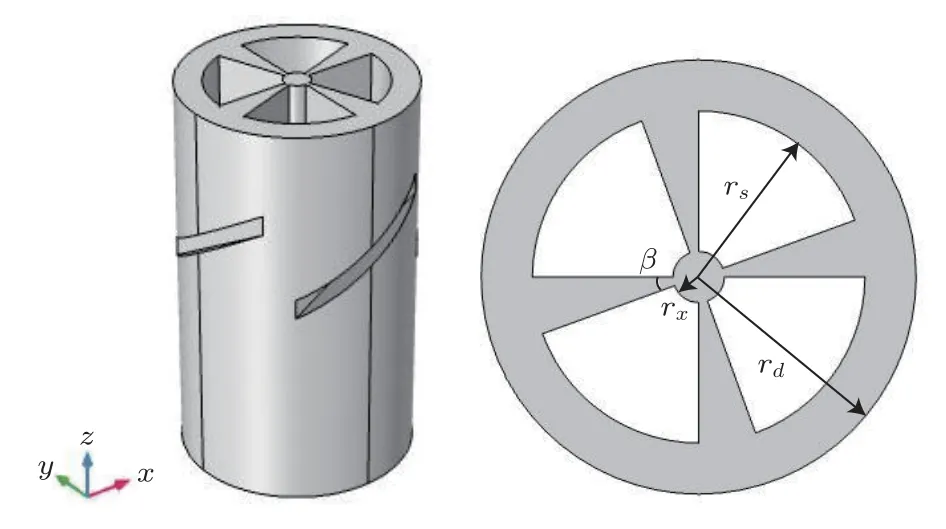
图5 基于周期性扇形孔和斜槽结构的振动转换体Fig.5 Vibration converter based on periodic fanshaped hole and chute structure
优化后的基于周期性扇形孔和斜槽结构的振动转换体可以提高系统的纵扭转换能力,因为:当夹心式压电陶瓷换能器产生的纵向振动传递到振动转换体上的斜槽结构时,斜槽位置的力被分解为两部分:法向力、剪切力,在剪切力的作用下,振动转换体产生扭转振动,进而导致4个扇形片产生剪切变形,此时,每个扇形片都可看作是一个长度为(rs-rx),宽度为1/2β(rs-rx)2的起剪切作用的弹簧,这4个剪切弹簧使振动转换体围绕半径为rx的圆柱进行扭转振动[17],即斜槽产生的剪切分力和4个起剪切作用的扇形片共同为振动转换体的扭转振动提供助力,所以,基于周期性扇形孔和斜槽结构的振动转换体能够更好地起到增大系统扭转分量的作用。为了验证结论的准确性,构造了如图6所示的基于周期性扇形孔和斜槽结构的模式转换型纵扭复合超声振动系统的模型,换能器和变幅杆的材料和结构参数保持不变,斜槽的结构参数保持不变,扇形孔结构的参数如图5~6所示。

图6 基于周期性扇形孔和斜槽结构的斜槽型复合模态超声振动系统的模型Fig.6 Model of the chute composite modal ultrasonic vibration system based on a periodic sectorshaped hole structure
对系统进行模态分析,同样搜索5~20 kHz频率范围内的谐振振型,结果如图7所示。

图7 基于周期性扇形孔结构的斜槽型复合模态超声振动系统的振型图Fig.7 Vibration modal diagram of chute type composite mode ultrasonic vibration system based on periodic sector-shaped hole structure
由图7能够看出,当特征频率为12226 Hz、18750 Hz时,纵扭复合超声振动系统表现为以纵振为主的振动型态;当特征频率为7896.6 Hz、11336 Hz、17477 Hz时,系统则表现为以扭振为主的振动型态。与基于斜槽结构纵扭复合超声振动系统相同,也以二阶扭转模态为例,计算基于周期性扇形孔和斜槽结构的系统与仅基于斜槽结构的系统二者辐射面的扭转分量对比,结果如图8所示。
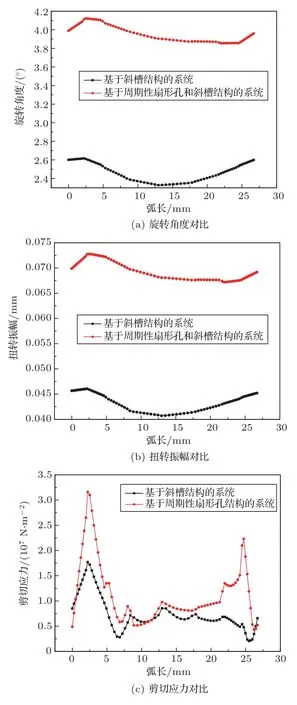
图8 有无扇形孔结构的系统扭转分量对比图Fig.8 Comparison diagram of torsional component of system with or without sector-shaped hole structure
从图8可以看出,基于周期性扇形孔和斜槽结构的系统的旋转角度从3.951°到4.111°,最大旋转角度是没有扇形孔系统的1.571倍,平均旋转角度是没有扇形孔系统的1.595倍;扭转振幅从0.0672 mm到0.0728 mm,其中,最大扭转振幅是无扇形结构的1.580倍,平均扭转振幅是无扇形结构的1.598倍;剪切应力从0.435×107N/m2变化到3.16×107N/m2,最大剪切应力是没有扇形孔系统的1.785倍,平均剪切应力是没有扇形孔系统的1.598倍,即引入扇形孔结构的系统的扭转分量得到了有效的提升。另外,为了更加清晰地看到扇形孔结构对系统性能的提升,图9给出了扇形片上的旋转角度和剪切应力的曲线分布。

图9 扇形片上的旋转角度和剪切应力Fig.9 Rotation angle and shear stress on the sector
从图9可以看出,基于周期性扇形孔和斜槽结构的振动转换体的旋转角度从2.923°变化到6.302°,最大旋转角度是未引入扇形孔结构时最大旋转角度的2.408倍;剪切应力从1.081×107N/m2变化到1.024×108N/m2,最大剪切应力是未引入扇形孔结构时最大剪切应力的5.785倍。即4个起剪切作用的扇形片的引入确实能起到增大系统扭转分量,提高纵、扭振动的转换效率的作用。
3 扇形孔结构参数对斜槽型纵扭复合超声振动系统性能的影响分析
为了获得扇形孔结构参数对系统纵扭转换能力的影响规律,分析了中心小圆的半径rx、扇形片的长度ls(ls=rs-rx)、扇形片的角度β(如图10所示)对以二阶扭转为主的纵扭复合超声振动系统谐振频率、旋转角度、扭转振幅以及剪切应力的影响,以找到最佳的扇形孔结构参数,仿真结果如图11~图14所示。
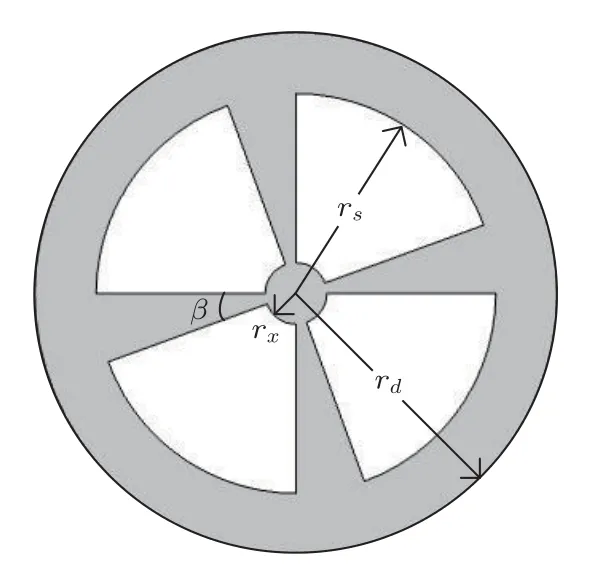
图10 扇形孔结构参数Fig.10 Fan-shaped hole structure parameters
从图11可以看出,当rs=13 mm、扇形片的角度β=11°均保持不变时,随着中心小圆半径rx的增大,系统的旋转角度、扭转振幅、剪切应力均呈现出先增大、后减小的趋势;在rx=2 mm时,旋转角度、扭转振幅和剪切应力均达到最大值;随着rx的增大,系统的谐振频率则呈现出先减小、后增大的趋势。由此可以看出,rx会对系统的性能产生影响,当rx=2 mm时,基于周期性扇形孔和斜槽结构的纵扭复合超声振动系统的性能可以达到最佳。

图11 rx对系统性能的影响Fig.11 The impact of rx on system performance
当rx=2 mm保持不变时,因为ls=rs-rx,即ls的大小只与rs有关。从图12可以很明显地看出,在rx=2 mm和扇形片的角度β=11°都保持不变时,随着rs的增大,系统的旋转角度、剪切应力以及扭转振幅均呈现出先减小、后增大的趋势。当rs=13 mm时,旋转角度、剪切应力以及扭转振幅全部达到最大;而随着rs的增大,系统的谐振频率则呈现逐渐减小的趋势。由此可以看出,rs的取值会对系统的性能产生影响,且rs=13 mm时,系统性能最佳。

图12 rs对系统性能的影响Fig.12 The impact of rs on system performance
由图13可以看出,当rx=2 mm、rs=13 mm保持不变时,随着β的增大,系统的旋转角度、剪切应力以及扭转振幅基本上均呈现减小-增大-减小-增大的趋势;在β=5°时,系统的旋转角度、剪切应力以及扭转振幅达到最大;而随着β的增大,系统的谐振频率则表现出先增大再逐渐减小的趋势。由此可以看出,β的取值大小也会对系统的性能产生影响,且β=5°时,系统性能最佳。

图13 β对系统性能的影响Fig.13 The impact of β on system performance
从上述分析能够得出:存在最佳的扇形孔结构参数的取值组合,使得以二阶扭转为主的基于周期性扇形孔和斜槽结构的纵扭复合超声振动系统可以获得最大的纵扭转换效率,且通过图11~图13可以确定扇形孔结构参数的最佳取值组合为:rx=2 mm、rs=13 mm、β=5°,此时的周期性扇形孔的尺寸如图14所示。

图14 扇形孔结构最终的尺寸参数Fig.14 The final size parameters of the fanshaped hole structure
建立当扇形孔结构参数取最佳值时的基于周期性扇形孔和斜槽结构的纵扭复合超声振动系统的模型,并将其与无周期性扇形孔结构的系统的性能指标进行对比,结果如图15所示。
由图15能够看出,引入最佳参数取值组合的基于周期性扇形孔和斜槽结构的系统的旋转角度从4.731°到5.025°,最大旋转角度是没有扇形孔系统的1.920倍,平均旋转角度是没有扇形孔系统的1.955倍;剪切应力由0.399×107N/m2变化到4.433×107N/m2,最大剪切应力是没有扇形孔系统的2.504倍,平均剪切应力是没有扇形孔系统的2.401倍;扭转振幅从0.085 mm到0.089 mm,最大扭转振幅是无扇形孔结构的1.935倍,平均扭转振幅是无扇形孔结构的1.961倍。为了更清楚地看到周期性扇形孔结构对系统各项性能的改善情况,表1给出了3种系统的性能指标值对比。从表1能够明显看出引入最佳参数组合的基于周期性扇形孔结构的纵扭复合模态超声振动系统的扭转分量得到了大幅的改善和提升。

性能指标无周期性扇形孔结构的系统基于周期性扇形孔结构的系统引入最佳参数取值组合的基于周期性扇形孔结构的系统旋转角度/(°)2.328~2.6173.951~4.1114.731~5.025剪切应力/(N·m-2)0.206×107~1.77×1070.435×107~3.16×1070.399×107~4.433×107扭转振幅/mm0.0407~0.04610.0672~0.07280.085~0.089
4 结论
周期性扇形孔和斜槽结构可以有效地改善模式转换型纵扭复合模态超声振动系统的纵、扭转换效率,增大扭转分量。论文主要分析了周期性扇形孔结构参数对基于周期性扇形孔和斜槽结构的纵扭复合超声振动系统纵扭振动转换效率的影响规律,并得到以下结论:
(1)因为斜槽产生的剪切分力和4个起剪切作用的扇形片共同为振动转换体的扭转振动提供助力,所以,基于周期性扇形孔和斜槽结构的振动转换体能够更好地起到增大系统扭转分量的作用;
(2)周期性扇形孔结构参数的改变能够对系统的旋转角度、剪切应力、扭转振幅以及谐振频率产生影响;
(3)基于本文所建立的模型进行分析后,发现:基于周期性扇形孔和斜槽结构的系统能够在很大程度上增大扭转分量,提高纵扭振动的转换效率。
