基于混沌-LSSVM神经网络的用电量短期精准预测算法
2022-11-21葛宇达沈杰周扬李大任陈茂佳甘泽鸿
葛宇达,沈杰,周扬,李大任,陈茂佳,甘泽鸿
(1.国网浙江省电力有限公司温州市洞头区供电公司,浙江 温州325700; 2.国网浙江省电力有限公司温州供电公司,浙江 温州325028)
用电量短期精准预测是电网调度进行管理决策的有效数据支撑,是确保电网安全、平稳运行、纠正电力偏差以及避免能源浪费的重要手段[1],实时负荷调度的控制方略以解决电网电量偏差问题,其核心即是需要准确掌握用户的用电量信息,对用户的用电量进行准确预测。用电量短时预测具有时效性强、精准度高的要求[2],在此前提下采取何种措施实现用电量短时预测既是国家电网实现需求侧管理需关注的重点问题,也关系着国家电网的经济利益,对电网的持续发展具有重要意义[3-4]。
具有较强随机性以及易受不确定性因素的影响是用户短期用电量表现出的显著特性,在对预测算法进行选取时需充分考虑短期用电量的特性,最大程度降低其特性对用电量预测的影响,才能有效提升用电量预测效果。乔黎伟等人针对传统用电量预测模型未能兼顾用电量各影响因素的问题,提出利用互信息法对用电量影响因素进行辨识,再通过随机森林法实现用电量预测模型的构建,以此完成中短期用电量的预测。该方法虽能降低不同用户模式对用电量预测质量的影响,但该方法具有局限性,仅能有效提升聚类中心周边用户的用电量预测效果[5];魏明奎等人提出利用最小二乘支持向量机(LSSVM)神经网络构建电力负荷预测模型,并通过粒子群算法实现模型参数的寻优,以提升短期电力负荷预测准确度,该方法确具有较好的预测性能,但受负荷时间序列关联因素的影响,使得负荷预测结果大打折扣[6]。因此,本文结合前人研究经验,有效结合混沌理论,提出基于混沌-LSSVM神经网络的用电量短期精准预测算法,通过对用电量混沌时间序列进行相空间重构,以达到用电量各影响变量关系辨识的目的,利用LSSVM神经网络实现用电量的短期预测,并通过参数优化提高用电量预测准确度。
1 用电量的短期精准预测
1.1 用电量混沌时间序列相空重构
用电量原始数据是通过某一时间间隔采样获取的时间序列数据,具有离散性特点,且用电量与时间呈非线性改变特性。基于混沌理论,混沌系统内所有变量信息均可通过时间序列进行反映[7],因此,本文通过重构相空间实现用电量隐含信息的分析。对于混沌系统而言,将任意时间点的状态称之为相,相空间是其状态的决定因素。根据Taken定理得出,系统内某一变量的改变与其决定因素的演化具有紧密关联性,对于混沌相空间重构问题,{x(t);t=1,2,…,N}表示采样获得的任意用电量时间序列,其长度表示为N,对其进行相空间重构,可得到x(t)={x(t),x(t+μ),…,x(t+(m-1)μ)},t=1,2,…,M,M=N-(M-1),其轨迹可通过下式进行描述:
X=[X1,X2,…,Xn]=

(1)
其中:对于相空间,其内一点表示为Xi,嵌入维度表示为m,延迟时间表示为μ。
确定m、μ是相空间重构的基础,由此可确保系统动力学形态得以复原,同时在保证原始数据间关联关系不变的情况下,避免发生信息、噪声冗余问题[8]。通过对时间序列进行相空间重构,可有效获取用电量的特征向量,确保用电量短期预测精度获得大幅提升。
(1)计算延迟时间
在对用电量时间序列数据进行相空间重构时,其中一个主要参数即为延迟时间,其值的选择至关重要。当μ过小,相空间轨迹将集聚于某一位置处,此时难于获取到完整信息,从而生成冗余误差;当μ过大,将使得临近时刻的动力学性态发生巨大改变,造成系统内信号严重失真,生成不相关误差。本文采用互信息法完成μ的确定,即获取互信息函数的首个最小值。
{x(t),y(t)}表示两组信号,设定y(t)=x(t+μ),t=1,2,…N,通过已知的x(t)的实测值对y(t)的信息量均值进行预估,公式描述为:
I(x,y)=H(x)+H(y)-H(x,y)
(2)
(3)
(4)
式中:对于信号x(t),其熵表示为H(x),用于描述测量N个x(i)获得的信息量均值。对由变量构成的样本空间进行网格划分,得到数个网格,分别计算各网格所含点数确定各变量的概率值,分别表示为Pxy[x(i),y(j)]、Px[x(i)]、Py[y(j)]。
(2)嵌入维数的计算
在对用电量时间序列进行相空间重构时,需确定的另一主要参数即为嵌入维数。本文利用Cao方法实现最近嵌入维数的确定,具体过程为:
{x(t);t=1,2,…,n}表示用电量时间序列,其长度为n,分别对其m维、m+1维相空间进行重构,对于m+1维相空间,其第i个相点表示为Xi(m+1),同理,对于m相空间,其第i个相点表示为Xi(m),Xj(m)(j=1,2,…k)为其最近邻域点,欧式距离表示为‖·‖,则有:
(5)
计算公式(5)的平均值,表示为E(m),其公式描述为:
(6)
时间序列由m维至m+1维相空间演化,其变化用下式进行描述:
(7)
在相空间轨迹上,当m不断增大,E1(m)的变化量越来越小,逐渐趋于稳定,由此可确定嵌入维数的最优值为m+1。
1.2 LSSVM神经网络的参数优化
支持向量机(SVM)的基本原理是采用非线性映射实现输入数据向高维空间转换,将其转变为不等式约束的二分类问题[9],与SVM相比,LSSVM的差异之处为LSSVM是通过等式约束,以误差平方和作为评价损失风险,并通过线性矩阵计算方式实现实际问题的求解。LSSVM的基本原理是:
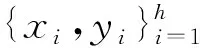
y=f(x)=Gφ(x)+b
(8)
式中:惯性权重因子表示为G,偏差表示为b,以最低结构风险作为目标函数实现LSSVM的线性回归[10],其公式描述为:
(9)
s.t.yi=GTφ(x)+b+δi
(10)
i=1,2,…,h
式中:正则化参数表示为λ,是对回归函数经验项重要程度的描述,经验风险随着该值的增大而减小,当经验风险值较低时,回归函数具有较低的泛化性能[11];松弛系数表示为δi,引入拉格朗日函数后,可将公式(9)描述为:
(11)
式中:拉格朗日乘子表示为ai,基于KKT条件可得:
(12)
对G、δi进行消除后,可得到公式(10)的解,其公式描述为:

(13)
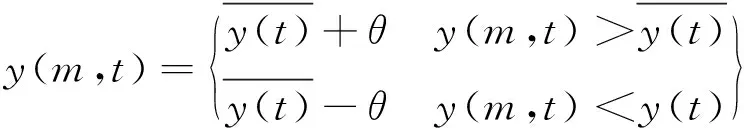
(14)
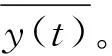
基于Mercer条件的核函数表示为K,其公式表示为:
K(xi,xj)=φ(xi)Tφ(xj)
(15)
由此可确定LSSVM的回归函数,其公式描述为:
(16)
K(x,xi)为非线性函数,可实现样本数据的高维空间映射。本文选用的核函数为径向基函数,其公式描述为:
(17)
式中:其宽度表示为σ。
通过对用电量混沌时间序列数据进行相空间重构,获取其特征向量,将其输入到LSSVM神经网络中构建用电量短期预测模型,实现用电量短期预测。由于参数λ、σ的取值对LSSVM神经网络的学习性能起决定性作用m、μ参数对相空间重构具有重要影响,因此,需对以上参数进行优化,确保用电量预测模型具有较好的预测效果。
2 用电量预测模型参数优化
2.1 用电量预测模型
m、μ、λ、σ是基于混沌-LSSVM的用电量预测模型的四个重要参数,各参数取值直接决定了该用电量预测模型的预测精度[12-13],因此,本文采用差分进化算法对其进行寻优,将适应度函数作为目标函数,在不断迭代运算中通过确定其最小值实现用电量预测模型参数组合(m、μ、λ、σ)的优化。基于差分进化的(m、μ、λ、σ)参数组合寻优的基本原理是在定义域内获取一组(m、μ、λ、σ)参数组合序列,将其视为DE算法的初始个体,利用此组参数对用电量预测模型进行训练,先计算模型预测均方差MSE值,再对各个体适应度值进行求解,在执行交叉、变异、选择过程中获取DE算法的子代种群,继续循环迭代,直至符合算法终止条件,由此实现参数组合(m、μ、λ、σ)的寻优,以最佳m、μ、λ、σ参数训练用电量预测模型,实现用电量的短期精准预测。通过下式对其适应度函数进行运算,公式描述为:
(18)
(19)
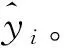
第一步:对参数进行设定,初始迭代次数t=0。
第二步:以混合编码方式对参数m、μ、λ、σ作编码处理,对m、μ作二进制编码,λ、σ为实数编码,通过混沌序列获得DE算法的初始种群。
第三步:通过对个体进行解码获得实际参数,通过参数m、μ的确定实现用电量混沌时间序列的重构,通过λ、σ参数训练LSSVM,对各组参数下的用电量预测准确度进行登记,并对所有个体的适应度值进行求解。
第四步:通过交叉、变异、选择获得子代种群,t=t+1。
第五步:对DE算法的停止迭代条件进行判定,当符合停止迭代条件,则转入下一步,反之,退回步骤三。
第六步:获得最佳参数m、μ、λ、σ。
第七步:以m、μ参数实现用电量混沌时间序列的重构,通过λ、σ实现LSSVM的训练,获得用电量短期精准预测结果。
2.2 用电量短期预测流程
本文通过构建的参数优化后的混沌-LSSVM神经网络预测模型实现用电量的短期预测,其流程如图1所示。
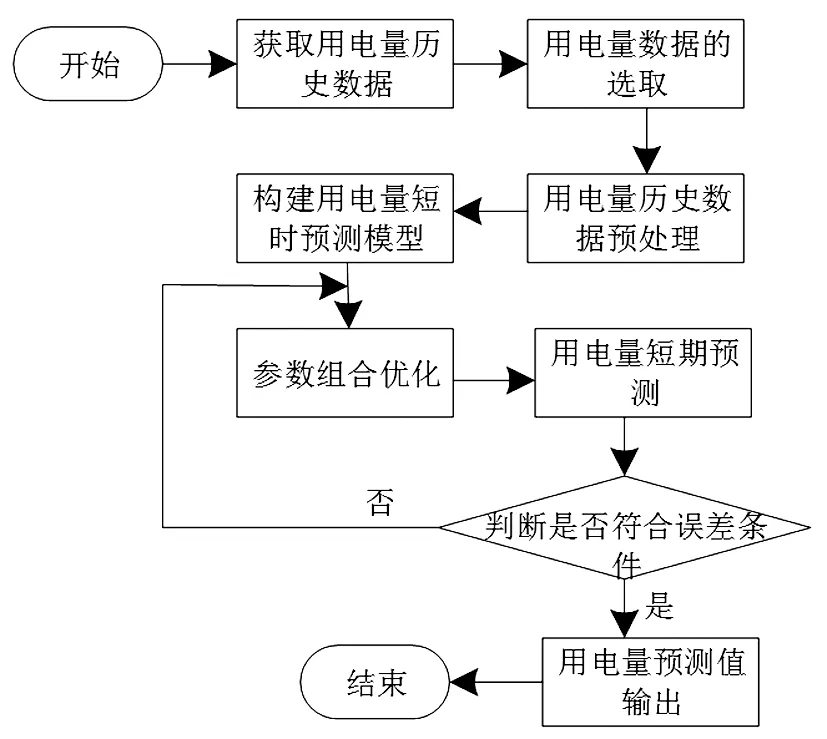
图1 用电量短期预测流程Fig. 1 Short term forecasting process of power consumption
用电量短期预测的具体流程为:
第一步:获取全面、完整的用电量历史数据,选取预测日前一天的相同时段用电量数据作为混沌-LSSVM神经网络预测模型的输入变量。
第二步:对历史用电量数据进行预处理[14],通过补充、更正操作解决历史用电量数据存在遗漏、异常的情况。
第三步:对用电量历史数据进行混沌时间序列重构,获取用电量特征变量,将其输入到LSSVM神经网络中,实现用电量短期预测模型的构建。
第四步:采用差分进化算法对混沌-LSSVM用电量短期预测模型的参数进行寻优,以确定最适合的参数组合。
第五步:利用最佳参数组合训练混沌-LSSVM用电量短期预测模型,获取用电量短期预测值。
第六步:判断用电量预测值是否符合最小误差条件[15-30],若满足条件,则将用电量预测结果输出;否则,退回到步骤四继续寻优,直至满足误差条件为止。
3 实验分析
以某地区历史用电量数据作为研究对象,将本文算法应用于该地区用电量短期预测中,分析本文算法的预测性能。利用设置于电能表上的传感器采集某地区2021年3月用电量数据,数据采集时间间隔为3分钟,构建历史用电量数据集,其中包括14880个计数点的用电量数据,将最后一天的480个计数点的历史用电量数据作为预测样本,其余全部为训练样本。
应用本文算法对历史用电量数据集时间序列数据进行相空间重构,通过对不同时间延迟时间μ下的互信息量变化情况进行分析,实现延迟时间的确定,实验结果如图2所示。
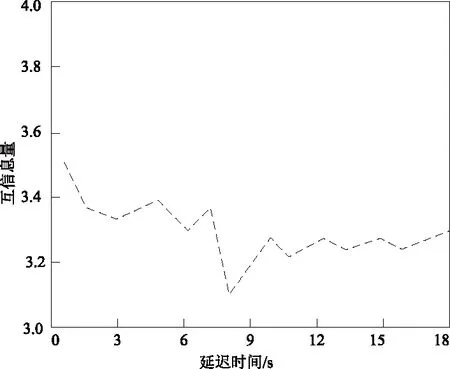
图2 不同时间延迟下的互信息量分析Fig.2 Analysis of mutual information under different time delays
分析图2可知,随着时间延迟的不断增大,互信息量开始呈现不断波动趋势,当延迟时间超过10s后,曲线慢慢趋于平稳,本文将互信息函数的首个最小值点对应的时间点作为延迟时间,因此可确定延迟时间为μ=8s。
在确定μ后,采用本文算法对相空间重构的嵌入维数进行确定,实验结果如图3所示。

图3 嵌入维数分析Fig.3 Embedded dimension analysis
分析图3可知,随着嵌入维数m的不断增加,E1(m)的值呈不断增大趋势,当m=7时,曲线走势趋于平缓,由此可确定嵌入维数为8。
设计三种用电量短期预测方案,具体内容为:
方案一:仅利用LSSVM神经网络对测试样本数据集进行预测;
方案二:在确定延迟时间为8,嵌入维数为8的前提下,采用LSSVM神经网络对测试样本进行用电量预测;
方案三:对参数组合m、μ、λ、σ进行优化,再利用优化后的混沌-LSSVM用电量预测模型(即本文算法)预测用电量。
分别应用三种方案对测试样本集用电量数据进行短期用电量预测,通过平均绝对百分误差(MAPE)、平均绝对误差(MAE)指标分析三种方案的预测性能,实验结果如表1所示。
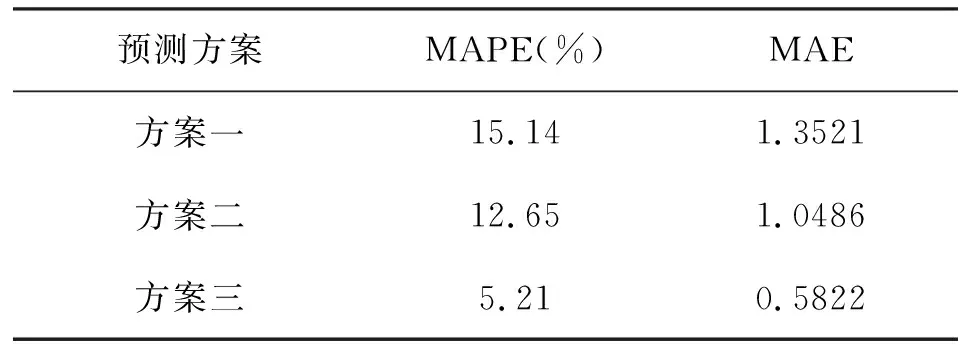
表1 三种方案的预测性能分析Tab.1 Prediction performance analysis of three schemes
分析表1可知,分别应用三种预测方案对用电量进行短期预测,MAPE、MAE指标值具有较大的差别,当采用方案一实现用电量短期预测时,二指标值均最大,高于其他方案,方案三的二指标值最小。实验表明,采用本文算法对各参数进行寻优后,可有效降低MAPE、MAE,提高用电量短期预测准确度。
采用本文算法对测试数据集不同计数点的用电量进行预测,因篇幅有限,仅给出该区域当日部分时刻的用电量预测结果,验证本文算法的预测能力,实验结果如表2所示。
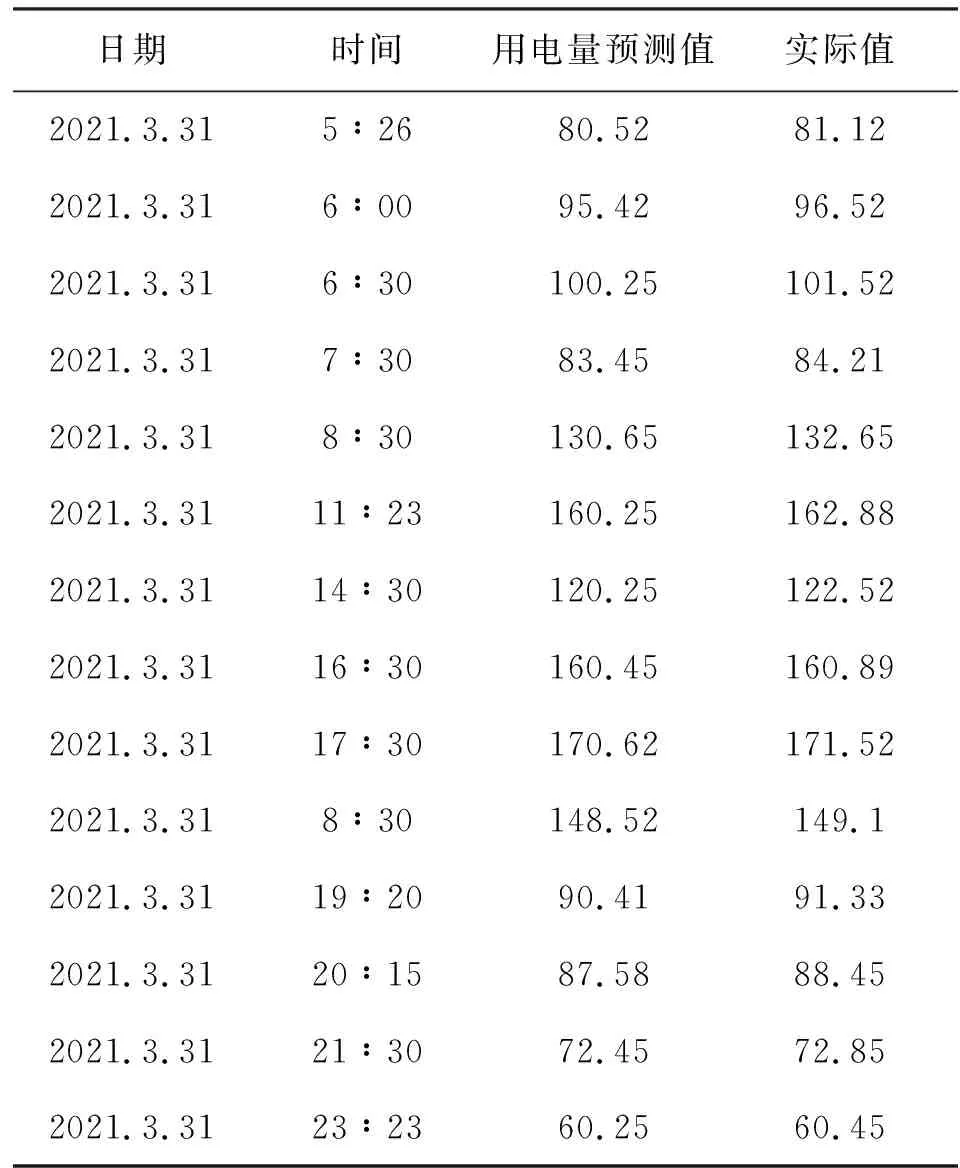
表2 某区域用电量预测结果分析Tab.2 Analysis of power consumption prediction results in a certain area
分析表2可知,本文算法可实现用电量的短时预测,且预测值与实际值存在较小差异,根据本文算法预测结果可有效衡量出该区域当日用电情况,在11∶30左右以及17∶00左右为用电量高峰期,供电部门可依据本文算法预测结果进行合理用电调度。实验结果表明,本文算法可有效提升用电量预测准确度,具有一定的应用性能。
4 结论
获取某区域2021年3月用电量数据建立历史用电量数据集,以此作为实验对象,将本文算法应用于用电量短期预测中,利用前30天用电量数据训练预测模型,将最后一天用电量数据作为测试数据,实现用电量的预测,验证本文方法的预测性能。实验结果表明:
(1)应用本文算法实现用电量短期预测,具有最低MAPE、MAE值。
(2)用电量预测结果与实际值误差较小。
