优化NGM(1,1,k)模型在国内能源消费中的应用*
2022-11-19石季雨余思瑶易叶青
石季雨,余思瑶,易叶青
(1.湖南人文科技学院,湖南 娄底 417000;2.韶关学院,广东 韶关 512005)
能源是经济增长的动力,当前我国正面临新一轮经济增长,居民消费结构升级,城镇化进程加快,经济社会发展对能源的依赖程度不断提高.因此,对中国国内能源需求形势进行科学、合理、准确的预测,不仅是保障中国能源安全,解决能源瓶颈的有效途径,而且是中国实现经济快速可持续增长的重要措施.目前,许多预测模型已经被开发出来用于预测国内能源的消耗.例如,赵飞[1]建立了基于残差自回归和自适应滤波的家庭能源消耗组合预测模型,并用该模型研究了中国的家庭能源消耗;梁武等[2]运用灰色无偏GM(1,1)模型研究中国国内能源消耗,并通过实例验证了模型的可行性和有效性;陈艺天[3]用ARIMA(2,2,0)模型预测中国人均国内能源消耗情况;何伟强[4]用小波分析理论研究了中国国内的能源消耗;冯兴来等[5]建立了基于函数变换的GM(1,1)模型,并用该模型对中国人均国内能源消耗进行了预测.在这些研究中,灰色预测模型的预测结果表现最好.
灰色预测模型最早由邓聚龙在国内提出,以预测精度高、小样本建模等特点被广泛应用于社会各个领域.NGM(1,1,k)模型是一种灰色预测模型,具有较高的预测准确度,但仍存在一些不足.为了弥补这些不足,研究人员花费了大量的时间和精力优化NGM(1,1,k)模型.例如,为了进一步提高 NGM(1,1,k)模型的预测性能,陈七榕等[6]使用复梯形公式优化模型的背景值,并基于复梯形公式建立了NGM(1,1,k)模型;童明余等[7]通过积分变换得到与NGM(1,1,k)模型的白化方程相匹配的灰度微分方程,推导出背景值优化公式,建立基于背景值优化的NGM(1,1,k)模型;鲁宝春等[8]建立了NGM(1,1,k)模型,并通过实例验证了模型的可行性和有效性,等等.这些改进的研究极大地促进了灰色预测模型的发展,丰富了灰色系统理论.
从以上改进可以看出,以往改进的模型大多是单一优化模型,缺乏双重甚至多重优化.为了进一步提高 NGM(1,1,k)模型的预测精度,笔者从 NGM(1,1,k)模型的背景值和时间响应函数2个方面对模型进行改进,基于背景值和时间响应函数的双重优化建立新的NGM(1 ,1,k)模型,并利用该模型研究中国国内能源消耗,以期更加准确地预测中国国内能源消费未来发展趋势,为政府、能源企业等决策者提供思路.
1 经典 NGM(1,1,k)模型
NGM(1,1,k)模型最早由崔杰等[9]提出,是一种预测精度较高的灰色预测模型,具体建模步骤如下:
第1步计算一阶累积生成序列.
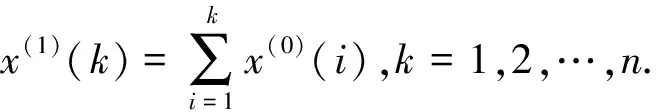
第2步建立NGM(1,1,k)模型.
x(0)(k)+ax(1)(k)=bk+c
(1)
是NGM(1,1,k)模型的原始形式.
x(0)(k)+az(1)(k)=bk+c
(2)
是NGM(1,1,k)模型的基本形式,其中
z(1)(k)=0.5×(x(1)(k)+x(1)(k-1))k=2,3,…,n
是NGM(1,1,k)模型的背景值,
(3)
是NGM(1,1,k)模型的白化微分方程.
第3步计算参数.
NGM(1,1,k)模型的参数a,b,c可以通过最小二乘法计算,即
其中
第4步建模预测.
首先根据NGM(1,1,k)模型的时间响应函数求解一阶累积生成序列的预测值,即
(4)
由于NGM(1,1,k)模型是基于一阶累积生成序列,因此需要将其归约为一阶累积归约来生成预测值序列,即
(5)
2 NGM(1,1,k)模型的优化
2.1 NGM(1,1,k)模型背景值的优化
由式(4)可以看出,NGM(1,1,k)模型的预测精度取决于参数a,b,c,而参数又与背景值密切相关.因此,背景值是影响模型预测精度的重要因素.在区间[k-1,k]上对式(3)进行积分:
可得

由式(4),白化微分方程(3)的解析方程可表示为
x(1)(k)=BeAk+Ck+D,
(6)
可得
x(0)(k)=x(1)(k)-x(1)(k-1)=B(eA-1)eA(k-1)+C,
(7)
可得
(8)
进一步可得
(9)
由于
x(0)(k)-x(0)(k-1)=B(eA-1)(eA(k-1)-eA(k-2)),
(10)
可得
(11)
然后
x(0)(k)=B(eA-1)eA(k-1)+C,
(12)
可得
C=x(0)(k)-B(eA-1)eA(k-1).
(13)
由式(6)可得
D=x(1)(k)-BeAk-Ck.
(14)
因此,优化后NGM(1,1,k)模型的背景值为
(15)
其中A,B,C,D可以通过式(9),(11),(13),(14)求解.
2.2 NGM(1,1,k)模型时间响应函数的优化
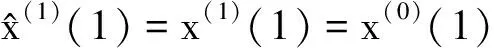
定理1已知存在一个非负原序列X(0),则对应的离散时间响应序列为
(16)
此时间响应函数的最优常数为
(17)
证明模型的约简序列从离散时间响应序列中得到,
(18)
构造误差平方和函数
为了求解误差平方和的最小值,让F′(C)=0,得到
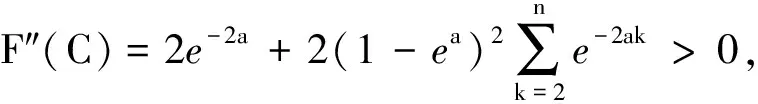
2.3 求解优化后的NGM(1,1,k)模型
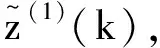
(19)
具体如下:
步骤2按照2.2节描述的方法计算模型的最优常数C*.

3 应用实例
本小节将通过实例展示该模型相对于其他模型的优越性,包括NGM(1,1,k)模型和GM(1,1)模型.
3.1 模型判断指标
采用几种广泛用于预测模型的误差度量来说明ONGM(1,1,k)模型的有效性和适用性.
(1)绝对百分比误差(eAPE).
(2)平均绝对百分比误差(eMAPE).
(3)平均绝对误差(eMAE).
(4)均方误差(eMSE).
(5)均方根百分比误差(eRMSPE).
(6)协议索引(Z).
3.2 实际应用预测
选取 2007—2013 年中国国内能源消费数据分别构建 GM(1,1)模型、NGM(1,1,k)模型和 ONGM(1,1,k)模型,2014—2017年的数据用于测试模型的预测准确性,数据均来自中国国家统计局(见表1).

表1 2007—2017年中国国内能源消耗原始数据(标准煤)
3种预测模型的预测结果如表2所示,模型的性能评价指标如表3所示.根据表2的拟合数据,3种预测模型的差异不大;根据表2的预测数据,3个预测模型均高估了实际值,但 ONGM(1,1,k)模型更接近实际值.根据表3所示的拟合指数,GM(1,1)模型拟合最佳,其次是 ONGM(1,1,k)模型,NGM(1,1,k)模型拟合最差;基于表3所示的预测指标,ONGM(1,1,k)模型对5个绩效评估指标都是最佳拟合.综上,ONGM(1,1,k)模型在这种情况下预测效果最好.
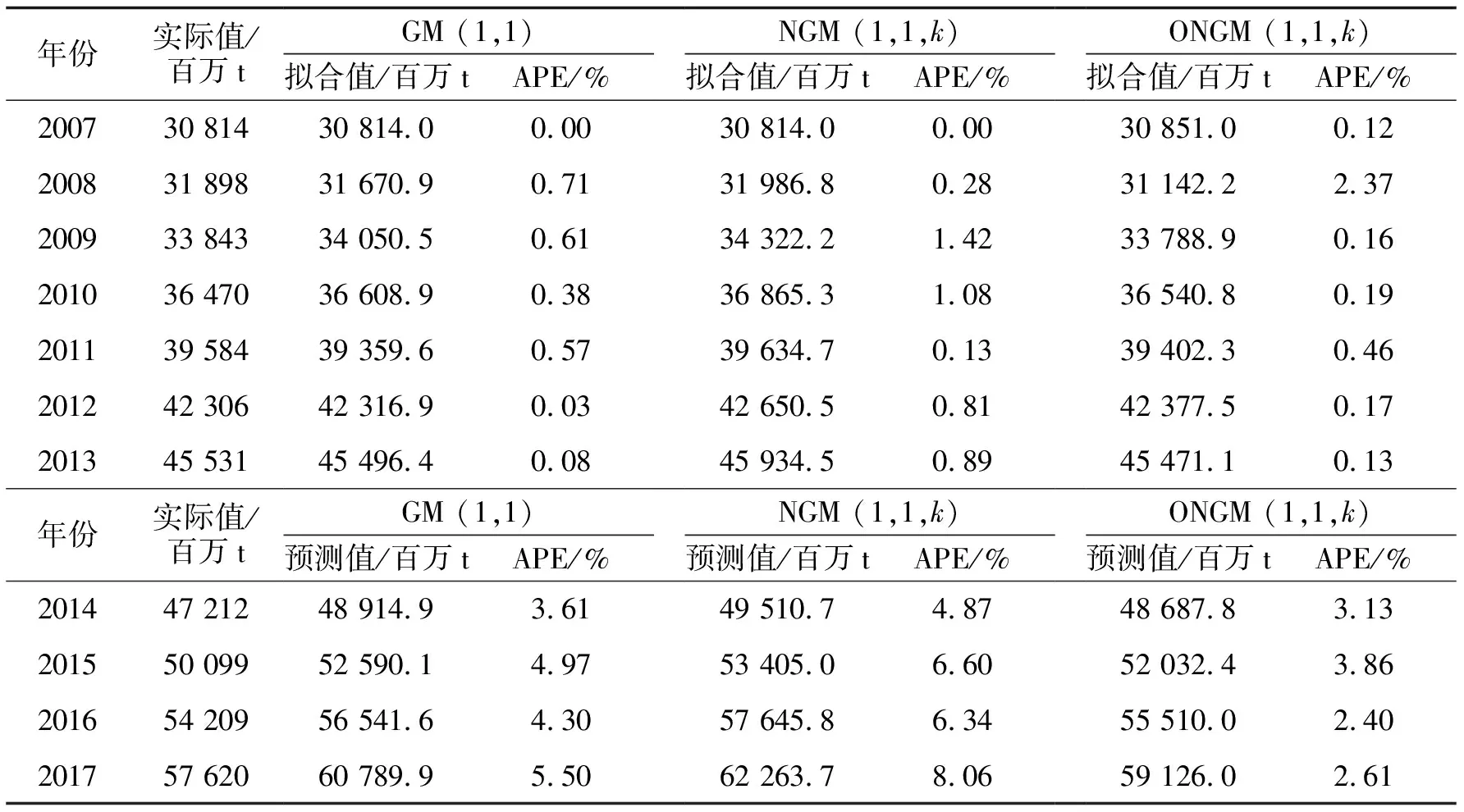
表2 3种预测模型的拟合和预测结果
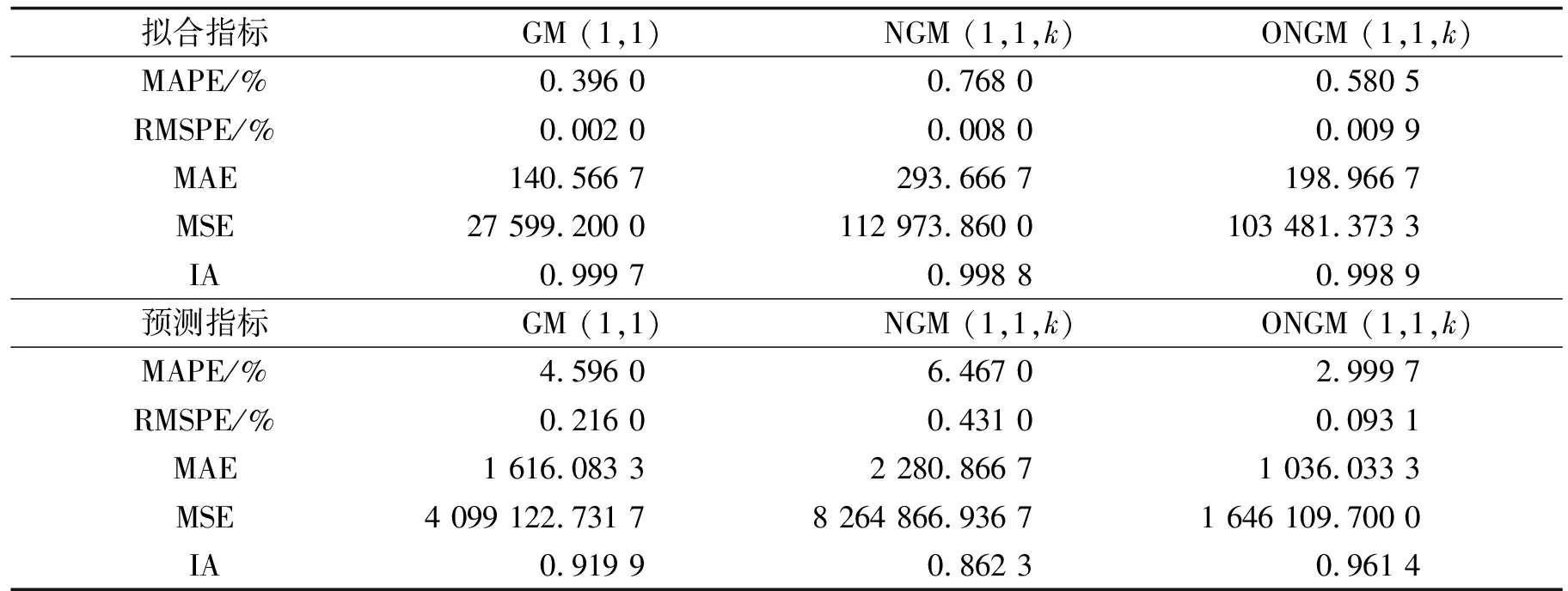
表3 3种预测模型的评价指标
3.3 代谢机制
代谢机制是提高预测模型准确性的有效措施.为了进一步提高 ONGM(1,1,k)模型的预测精度,本研究将代谢机制与ONGM(1,1,k)模型相结合.基于代谢思想的ONGM(1,1,k)模型的预测过程如下所示.设原始数据集的长度为n,营业额建模预测的周期数为d=5(其中灰色预测模型的预测精度更准确),代谢机制的步骤如下:
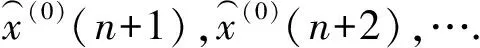
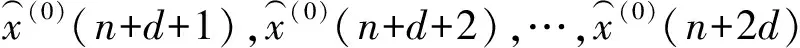
步骤3重复步骤2,使用最新的序列预测下一组数据点d,直到完成所需数量的预测.
3.4 预测
由于 ONGM(1,1,k)模型在3.2小节中表现出最好的预测性能,因此本小节使用基于代谢机制的 ONGM(1,1,k)模型预测未来5年中国国内能源消耗情况,结果如表4所示.

表4 未来5年中国国内能源消耗预测值(标准煤)
根据表4的预测值可以看出,到2023年,中国国内能源消费量可能会超过10万(百万t标准煤),随着年份的增加,中国的能源需求预测值也持续上升,这显然是合理的.因为随着中国继续城市化,国内的能源需求将在很长一段时间内继续增长.面对当前形势,为保障我国经济健康可持续发展,我国应加快能源比重改革,提高能源利用效率,大力发展可再生能源,节约能源支出,加快实施能源战略和相关法律法规.
4 总结
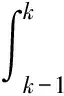
本研究将优化后的ONGM(1,1,k)模型应用于中国国内能源消费预测,与其他2种预测模型相比,该模型的各项预测指标都非常出色,能够更好地反映中国国内能源消费的实际趋势,因而具有一定的实际应用价值.
