考虑概率型共因失效的多阶段任务系统可靠性分析模型

王 鹏, 孙紫荆, 张 帆, 肖国松

(1. 中国民航大学民航航空器适航审定技术重点实验室, 天津 300300;2. 中国民航大学安全科学与工程学院, 天津 300300)

0 引 言

多阶段任务系统(phased-mission system, PMS)常见于现代复杂工程系统中,由多个连续不重叠的子阶段组成,系统成功完成各子阶段的任务即认为系统任务成功[1]。在系统运行的不同阶段中,同一元件的工作模式以及系统配置、失效标准等都可能随阶段的切换而发生改变。系统中元件或模块的跨阶段相关性使得PMS的可靠性评估具有更高的难度。

传统可靠性分析多基于独立性假设,即系统中各元件失效相互独立。而事实上,复杂系统的失效率普遍高于基于相互独立假设条件下的评估值,“相关”是失效的普遍特征[2]。共因失效(common cause failure, CCF)作为相关失效的主要因素,已有学者就CCF参数模型[3-5]构建与共因相关的系统可靠性评价方法[6-8]等方面开展诸多研究。

相比于单阶段系统,考虑CCF问题的PMS可靠性模型与评估需要更关注CCF条件下元件的跨阶段相关性问题。文献[8]提出考虑CCF的PMS显式分析法,将共因事件与受影响元件以逻辑“或”形式串联,以二元决策图(binary decision diagram, BDD)分析不可修PMS。文献[9-10]以后向递归算法求解CCF下的PMS可靠性,将共因事件视为新增元件引入系统模型中,定量计算的复杂程度依赖于共因事件及受影响元件的数量。除此之外,文献[11]提出概率型CCF(Probabilistic CCF, PCCF)的概念,即CCF事件以一定的概率发生且以一定概率造成多部件同时失效,区分于确定型CCF,即传统CCF问题。文献[12]提出基于BDD的显式与隐式方法分析PCCF问题。文献[13-14]在此基础上进一步提出适用于PMS系统的PCCF显式与隐式分析方法。文献[15]提出以隐式BDD法处理共因事件的发生服从随机分布的PMS可靠性分析模型。文献[16]提出综合应用BDD与Markov模型的模块化分析方法,能够处理系统动态行为。显式分析方法建模逻辑简单,但受共因事件数量及受影响元件数量影响,模型规模难以控制。隐式分析方法首先建立不考虑CCF的系统模型,而在模型的定量评估中引入共因因素,其模型规模与计算复杂度较显式模型都有一定改观。

贝叶斯网络(Bayesian networks, BN)作为对概率关系的有向图解描述,善于处理变量不确定性和相关性问题,可以应用于CCF问题的量化分析[6-8]以及PMS的描述表征[17]。同时,BN能够通过网络节点参数设置实现系统动态模块的表征[18-19],无需转化为状态空间模型进行分析,因此以BN进行可靠性分析更加灵活、适用范围更广。BN应用于CCF问题的分析常借助α因子模型[6]、β因子模型[19-22]等参数模型,将相关元件的失效事件划分为独立失效事件与CCF事件,对网络节点进行扩展以表征CCF事件,但扩展后BN中的新增节点数量随着受影响元件数量的增加呈指数增长。文献[23]提出基于BN处理CCF问题的新思路,适用于PCCF问题且能够有效减少新增节点数量、限制模型规模,但该方法仅适用于单阶段任务系统。

综上,对CCF问题研究主要限于单阶段任务系统,PMS的CCF问题更为复杂,当前已有的分析方法存在不同方面的问题。例如,缺乏对PCCF问题的考虑,建模分析过程繁琐、涉及两种以上模型的构建及转换问题,模型规模难以控制等。因此,提出一种新的基于BN的PMS系统可靠性分析模型。首先,研究基于BN的PMS表征方法,建立不考虑CCF的PMS基础BN模型，即PMS-BN。其次,构建各共因事件组合的共因空间,引入共因空间节点,并给出系统模型参数修正方法。最后,以共因节点及相关参数对不考虑CCF的PMS基础BN模型进行扩展,形成PCCF-PMS模型,能够实现考虑CCF影响的PMS可靠性量化分析。PCCF-PMS模型能够处理概率型CCF问题,且经简单变换能够同时实现对确定性CCF问题的分析,对多个共因事件间的统计关系没有特殊要求,同时网络模型的新增节点数可控,有效降低模型复杂度。

1 问题说明

在考虑CCF的情况下对PMS进行建模与可靠性分析,其中CCF问题包括确定型CCF与概率型CCF,PMS与共因事件遵循以下基本假设。

1.1 PMS基本假设

(1) 系统为二态系统,即元件与系统都只包含“正常”与“失效”两种状态。

(2) 系统运行中元件失效不可修复,一旦某元件在运行中由“正常”转为“失效”,则在后续任务时间中一直保持“失效”。

(3) 系统不同阶段间具有连续性,即各元件在下一阶段开始时的状态与上一阶段结束时状态相同。且系统从某一阶段到下一阶段的重新配置过程不存在失效。

(4) 系统在某一阶段出现失效,并不意味着在后续阶段一直失效,重新配置可能使系统恢复到正常运行状态。

(5) 后续分析过程中认为系统未失效即系统在其运行各阶段均未失效。

1.2 共因事件基本假设

(1) 系统运行中可能出现多个不同的共因事件,记为CCi(i=1,2,…,m)。某一共因事件是确定型或概率型需要依据其对系统元件的影响情况确定,因此在共因事件的表征符号上不做区分。

(2) 这些共因事件可能影响任务的一个阶段或多个不同的阶段,CCji(X)表示在阶段j中影响元件X的第i个共因事件。

(3) 不同的共因事件之间可能相互独立、相关或相斥。

(4) 共因事件的发生概率为一固定概率值,其统计关系可通过工程经验值及系统运行统计数据等确定,案例中相关数值作为输入参数直接给出。

2 基于BN的PMS模型表示

2.1 BN

BN是基于图论与概率论的不确定推理模型,直观的表现为赋值有向无环因果关系图,由有向无环图及其相应的条件概率关系组成。一个n节点BN可以用N=〈〈Ω,E〉,P〉表示。

(1) 网络结构G

G=〈Ω,E〉表示BN结构,即一个具有n个节点的有向无环图。集合Ω={X1,X2,…,Xn}中的元素为节点变量,E表示网络节点间的有向边。网络构建过程中的变量选取顺序对最终网络形式有很大影响,考虑复杂度与BN关系的可读性,通常依据变量间的因果关系和依赖关系构建BN。

对于网络中的节点Xi与Xj,有向边由Xj指向Xi表示节点Xj为Xi的父节点,Xi的父节点集合表示为pa(Xi),Xi的非后代节点集合表示为A(Xi),没有父节点或没有子节点的节点分别称为根节点和叶节点。在给定pa(Xi)情况下,Xi与A(Xi)条件独立,即

P(Xi|pa(Xi),A(Xi))=P(Xi|pa(Xi))

(1)

(2) 网络参数P

P表示与网络中各节点相对应的条件概率分布(conditional probabilities distribution, CPD)或条件概率表(conditional probabilities table, CPT),由于前述BN的条件独立性,CPD可以表示为P{Xi|pa(Xi)}。通过为网络中节点指定边缘概率分布或CPD,贝叶斯模型可推导得出包含所有节点的联合概率分布:

(2)

BN推理已有诸多成熟算法进行概率推理与最大后验概率解释[24-29],在构建系统BN模型后可以依据网络节点联合概率分布计算系统可靠度:

P[OUTCOME=0|Pa(OUTCOME)]

(3)

2.2 PMS

PMS由多个子阶段组成,系统在连续不重叠的子阶段中依次执行指定任务。系统在不同阶段中的配置形式、失效标准等可能都不相同。系统在某一阶段出现失效,并不意味着在后续阶段一直失效,重新配置可能使系统恢复到正常运行状态。

一个有3个运行阶段的简单PMS系统如图1所示,阶段1中元件B、C并联后与原件A串联,阶段2中元件A、B串联后整体与元件C并联,阶段3中元件A、B、C构成2/3(G)结构。

图1 示例PMS系统

2.3 基于BN的PMS模型元素表示

基于BN的PMS模型元素表示遵循由下而上的分层表示与由单阶段到多阶段的推广联系原则。

由下而上的分层模型元素表示用于建立系统各任务阶段的单阶段BN模型。单阶段模型元素可分为元件节点、模块节点、子系统节点与系统节点。其中,元件节点为BN根节点,系统节点为BN叶节点。模块通常为系统中构成并联、串联、表决结构等的元件组成,子系统依据系统中的子功能进行划分,模块节点与子系统节点可能重合或无必要,可依据待分析系统的实际组成情况进行删减。

由单阶段到多阶段的推广联系用于建立各任务阶段间的联系,在单阶段BN模型中,表示某一元件、模块或子系统的节点仅出现一次。而在多阶段BN中,同一元件、模块或子系统则在各阶段中以不同节点来表示,以角标加以区分,同时以有向边加以联系。除此之外,新增阶段节点来表示不同任务阶段。各节点的表征方式如表1所示。

表1 基于BN的PMS模型节点表示

3 基于BN的PMS可靠性分析模型建立

PMS-BN模型的建立过程首先需建立包含系统不同运行阶段的BN网络结构,在明确网络结构后,可依据现有研究成果确定网络节点参数[18,30-31]。网络结构的构建主要包括分阶段模型构建与阶段间模型整合两部分。

3.1 分阶段模型构建

分阶段模型构建过程与单阶段系统BN模型构建过程相同,可以依据对系统构成及运行原理的分析,进行由下而上的分层节点表示,并以系统组成元件间的因果或依赖关系进行构建,或依据系统故障树模型进行转化得到。对于在不止一个系统运行阶段中发挥作用的元件,在不同阶段中以不同的节点表示。典型常见结构的BN模型如图2所示。

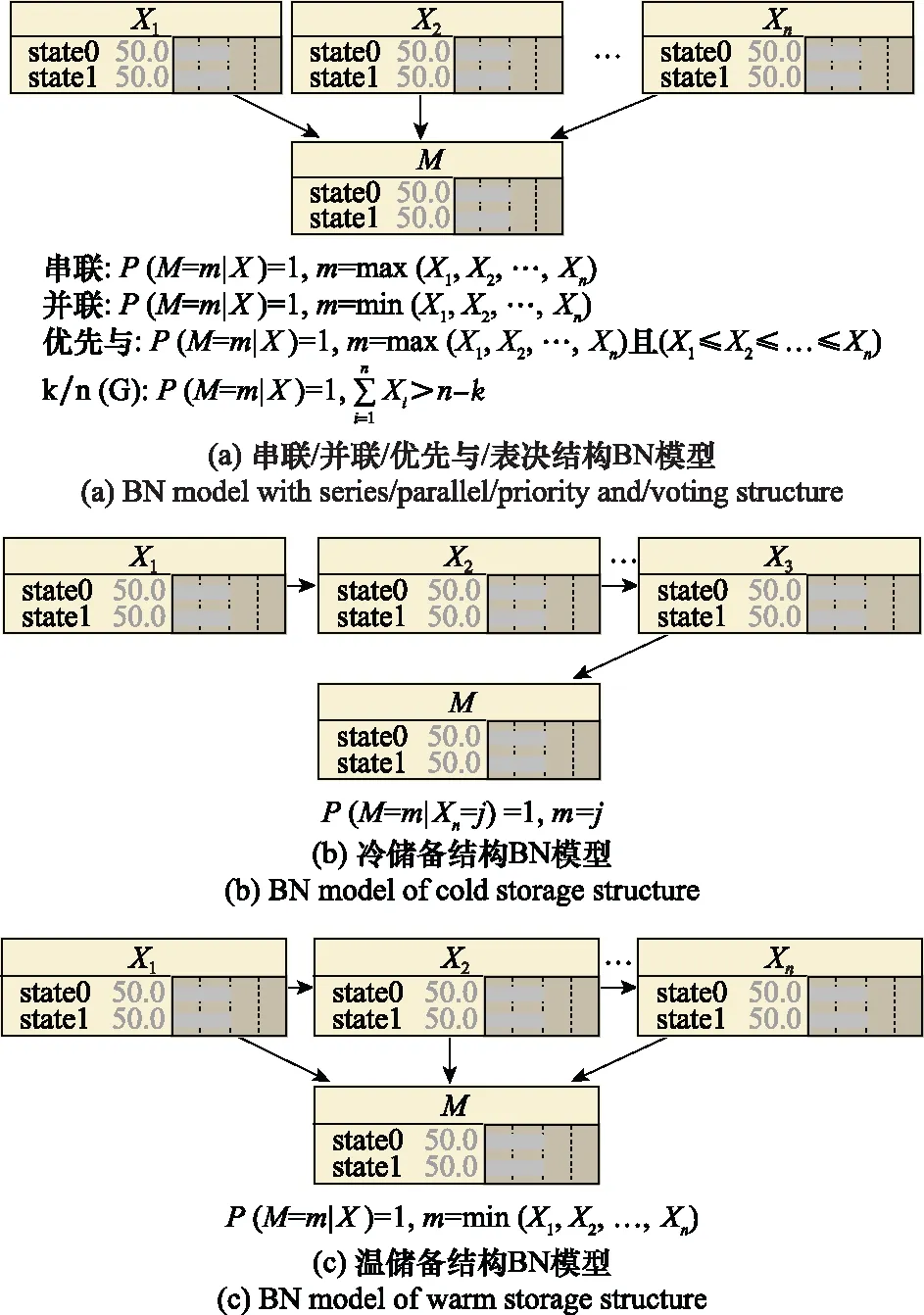
图2 典型常见结构的BN模型

3.2 阶段间模型整合

阶段间模型整合过程需要将系统的分阶段模型进行整合连接,形成多阶段系统的整体网络模型,即PMS-BN模型。

(1) 系统中同一元件在不同运行阶段中的状态是相关的,因此以有向边连接同一元件在不同阶段间的对应节点。

(2) 对网络整合过程带来的某些节点间的独立性变化进行特殊考虑,依据具体系统的实际运行情况,适当添加有向边对网络模型进行修正。

例如,考虑下述结构：元件A、B在系统运行的第1阶段为并联关系,第2阶段元件B为元件A的储备。A1和A2分别表示阶段1与阶段2中的元件A。同样的,对于不同阶段中的同一模块、子系统以及系统整体也以不同节点表示,图3中T1和T2分别为阶段1与阶段2的系统节点。

图3 PMS分阶段BN模型

单独考虑系统第2阶段网络模型,系统节点T2的状态完全取决于B2,而与A2无关。但在对系统分阶段的BN模型进行整合的过程中,考虑到元件B可能已经在阶段1中失效,并不能在阶段2中起到储备作用,因此节点T2的状态可能依赖于节点A2,需要在节点A2与节点T2之间添加有向边。如图4所示,依据步骤1, A1、A2与B1、B2节点间分别添加有向边。依据步骤2,考虑独立性变化,在A2、T2节点间添加有向边。其他网络结构与分阶段模型相同。

图4 PMS联合BN模型

(3) 仅当各任务阶段均都未失效时,认为PMS整体未失效。因此,添加最终系统节点作为各阶段系统节点的共同子节点,如图4中节点S,表征多阶段系统最终状态,各阶段系统节点间的逻辑关系为串联,如图4中节点T1、T2即为串联关系。

依据上述PMS-BN模型构建过程对图1中系统进行建模,如图5所示。其中M11、M21分别表示阶段1中第1个模块、阶段2中第1个模块,T1、T2、T3分别表示3个运行阶段对应的系统节点,节点S为最终系统节点。

图5 示例系统的PMS-BN模型

4 PCCF-PMS模型建立

PMS-BN能够实现对PMS系统的基本建模,但并未涉及对CCF问题的考虑。因此,以PMS-BN模型为基础,提出PCCF-PMS模型,能够在实现对PMS表征的同时,综合处理确定型CCF与概率型CCF问题。

对共因事件空间进行划分,研究在不同共因空间影响下,相关元件节点对应的条件概率。扩展模型的网络结构相比原多阶段模型,仅在其基础上进行少数节点及有向边的添加,CCF对系统影响的引入通过相关节点条件概率的修正实现。有效避免复杂系统多个元件受多个共因事件综合影响时BN模型新引入节点过多、原始数据难以获取等问题。

PCCF-PMS模型构建包含两部分:网络结构扩展与网络参数确定。网络结构扩展即在原有多阶段模型基础上引入与共因事件相关的新节点,网络参数确定即为新节点以及受共因事件影响的系统元件节点赋予概率推理所必需的条件概率关系。

4.1 网络结构扩展

(1) 共因空间节点

共因空间节点CCE表示影响系统的所有共因事件发生或未发生的组合。当系统受到n个共因事件CCi(i=0,1,…,n)的影响,则共因空间为2n个不相交子空间的集合,记为CCEk(k=0,1,…,2n-1)。对于CCi=1,有集合S={i},则

(4)

图6 CCE节点与相关子节点链接

(2) 受共因事件影响的元件节点

受共因事件影响的元件在系统各运行阶段对应的网络节点均不需做模型结构上的扩展,仅从原模型的根节点变为共因空间节点CCE的子节点,以有向边与CCE节点连接,如图6所示。

4.2 网络参数确定

(1) CCE节点参数

依据前述有关共因事件的基本假设,系统运行中可能出现n个共因事件CCi(i=1,2,…,n),且这些共因事件之间可能存在相互独立、互斥或统计相关等关系。共因事件间的相互关系直接影响后续节点参数的确定,因此需先明确共因事件间的关系。

表2 CCE节点概率分布

设存在3个共因事件CC1、CC2、CC3,其中CC1与CC2互斥,CC2与CC3相关,则各共因空间概率如表3所示。

表3 三共因事件对应的共因空间发生概率

(2) 受共因事件影响的元件节点参数

在每个阶段不同共因事件发生的条件下,评估受共因事件影响的所有元件的总条件失效概率。

设qjX为元件X在阶段1至阶段j-1中都未失效的条件下的独立失效概率,qjiX为在阶段j中影响元件X的第i个共因事件发生的条件下,元件X的条件失效概率,即qX|CCji(X)。若在共因空间CCEk下,阶段j中元件X被m个共因事件(CCj1(X),CCj2(X),…,CCjm(X))影响,则元件X在阶段1至阶段j-1中都未失效的条件下,在阶段j中失效的总条件概率QjkX为

(5)

给出元件X受共因空间影响而失效的条件概率表,如表4所示。表4中,元件X在阶段j中受第i个共因事件影响而失效的条件概率值qjiX,在对具体系统进行分析时需要依据实际情况进行赋值,若共因事件CCji(X)的发生导致元件X必然失效,即此时该共因事件为确定性共因事件,则令qjiX=qX|CCji(X)=1。

表4 元件X的条件失效概率

PCCF-PMS模型确定网络结构及网络参数后,即可依据式(3)进行可靠度分析,在后续案例计算中模型构建与推理计算通过贝叶斯分析工具Netica及BNT进行。

5 实例分析

将提出的PCCF-PMS模型应用于地球同步轨道卫星的首次变轨的任务可靠性分析[16]。文献[16]中提出模块化方法,将BDD与Markov链模型分别应用于系统静态与动态模块以实现对相关可靠性问题的分析。

5.1 系统概述

文献[16]中地球同步轨道卫星系统的首次变轨任务包含5个运行阶段,即太阳捕获、地球捕获、地球指向、点火准备、远地点点火,姿轨控和推进分系统组件如表5所示。其中,组件E星敏感器在地球同步轨道卫星系统首次变轨任务的各个阶段均未涉及,因此在定量分析中不再列出。

表5 姿轨控和推进分系统组件

有3个外部共因事件分别作用于系统运行的第4阶段与第5阶段,共因事件CC1作用于阶段4,可记为CC41,共因事件CC2、CC3作用于阶段5,分别记为CC51、CC52,其中CC41分别与CC51、CC52统计独立,CC51与CC52统计相关。系统定量分析所需的输入参数如下。

(1) CCF组PCCG(受某一共因事件影响的元件集合):PCCG41={A,C,G},PCCG51={B,D,F},PCCG52={A,C,G}。

(3) 元件X在阶段j中的独立失效率λjX(单位为min-1):λjA=2.44×10-8,λjB=1.22×10-8,λjC=6.10×10-8,λjD=2.44×10-8,λjF=1.72×10-8,λjG=1.22×10-8。

(4) 在阶段j中第m个共因事件发生时元件X的条件失效率λjmX(单位为min-1):λ41A=2×10-4,λ41C=3×10-4,λ41G=7×10-4;λ51B=1×10-4,λ51D=2×10-4,λ51F=3×10-4;λ52A=5×10-4,λ52C=6×10-4,λ52G=4×10-4。

(5) 阶段j的持续时间Tj(单位为min):T1=45,T2=698,T3=35,T4=120,T5=57。

5.2 系统网络模型构建与可靠性分析

(1) PMS-BN模型

依据第3.2节中方法构建上述系统的基础BN模型,如图7所示。网络中根节点为系统中各元件,节点Tj(j=1,2,3,4,5)为系统某一阶段节点,节点S为系统节点。各阶段节点间逻辑关系为串联,即当各阶段均未失效时,认为PMS系统成功运行。

图7 卫星系统首次变轨任务的PMS-BN模型

(2) PCCF-PMS模型

① 共因空间节点CCE

对3个共因事件进行共因空间进行划分,形成8个不相交的共因子空间集合。

共因事件CC51与CC52间统计相关,依据第4.2节计算CCE节点概率,如表6所示。

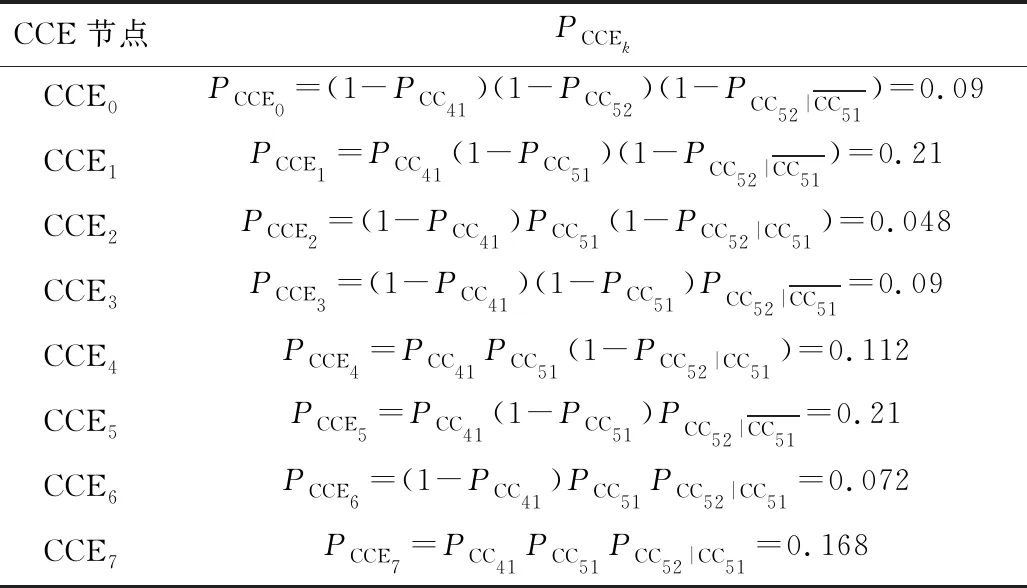
表6 CCE节点概率表

② 元件节点CPT

对受到共因事件影响的系统元件节点参数进行修正,由根节点边缘概率变为在共因空间影响下失效的条件概率。以元件A、B为例说明计算过程,并给出所有相关元件在共因空间影响下的条件失效概率。

对于元件A,在阶段四中受共因事件CC41的影响,即受共因子空间CCE1、CCE4、CCE5、CCE7的影响。而在阶段5中,元件A受共因事件CC52的影响,即受共因子空间CCE3、CCE5、CCE6、CCE7的影响。

根据式(5),在阶段4中,j=4,m=1,则

P(A4|CCEk)=q4A=λ4AT4=0.000 002 928,k=0,2,3,6P(A4|CCEk)=1-(1-q4A)(1-q41A)=1-(1-λ4AT4)(1-λ41AT4)=0.024 002 858,k=1,4,5,7

在阶段5中,j=5,m=2,则

P(A5|CCEk)=q5A=λ5AT5=0.000 001 390 8,k=0,1,2,4P(A5|CCEk)=1-(1-q5A)(1-q52A)=1-(1-λ5AT5)(1-λ52AT5)=0.028 501 351,k=3,5,6,7

对于元件B,受阶段5中共因事件CC51的影响,即受共因子空间CCE2、CCE4、CCE6、CCE7的影响。根据式(5),j=5,m=1,则

P(B5|CCEk)=q5B=λ5BT5=6.954E-7,k=0,1,3,5P(B5|CCEk)=1-(1-q5B)(1-q51B)=1-(1-λ5BT5)(1-λ51BT5)=0.005 700 691,k=2,4,6,7

其他元件计算过程不再赘述,共因组中所有相关元件在各共因子空间下的条件失效概率如表7所示。需要说明的是,元件B、C、D、G在阶段5中并不参与系统运行,但其相关节点在共因事件影响下的条件概率计算结果仍在表7中列出。在图7所示系统BN模型基础上引入CCE节点,并对受共因事件影响的元件节点CPT进行修正,得扩展后的系统BN模型如图8所示。

表7 相关元件在各共因子空间下的条件失效概率

图8 卫星系统首次变轨任务的PCCF-PMS模型

③ 系统可靠性分析

不考虑PCCF因素,以图7所示PMS-BN模型对卫星首次变轨任务的可靠度进行分析,可靠度曲线如图9所示。则在此情形下,任务可靠度为0.999 88。 考虑PCCF因素影响,以图8所示PCCF-PMS模型进行计算分析。共因事件发生在任务第4、第5阶段,这两阶段的可靠度对比如图10所示。随着运行时间增加,系统可靠度逐渐下降。当考虑PCCF因素影响时可靠度为0.932 32,与文献[17]相同,考虑PCCF因素影响时系统可靠度显著低于不考虑PCCF因素时的可靠度。

图9 不考虑PCCF的系统可靠度

图10 考虑与不考虑PCCF影响的可靠度对比

对考虑与不考虑PCCF影响时的可靠度差值进行计算,如图11所示。当系统任务进行到第818 min,即在受PCCF影响的40 min后,系统考虑PCCF的可靠度相较不考虑PCCF的可靠度低0.01,已经达到10-2数量级,而最终误差将达到0.067 5。因此,对PCCF因素的考虑在PMS可靠度分析工作中不容忽视。

图11 考虑与不考虑PCCF影响的可靠度差值

对当前较为成熟的CCF问题处理方法进行整理,与基于BN的PCCF-PMS模型进行对比,如表8所示。

基于BN的PCCF-PMS模型能够处理PMS的PCCF问题,对共因事件间的关系没有独立性要求,模型规模不会随着共因事件数量或受影响元件数量的增加出现大幅扩张。且由于BN的本身特点,系统模型构建以及系统动态行为表征较其他方法更为灵活。系统BN模型的构建可由系统故障树转换得到,也可依据对系统的分析直接构建。系统动态结构的表征可以直接通过网络节点参数设置实现,而不需要转化为状态空间模型进行分析。

6 结 论

本文提出一种PCCF-PMS模型,能够分析受CCF影响的PMS任务可靠性:① 建立不考虑CCF的PMS-BN模型,实现PMS系统不同阶段模型的联合;② 对共因空间进行划分,确定共因空间发生概率及受影响元件在各共因空间下的条件失效概率;③ 对PMS-BN模型进行扩展,并依据修正后的网络参数建立系统PCCF-PMS模型。

PCCF-PMS模型能够分析受多个概率型CCF问题影响的PMS可靠性,若影响系统的多个共因事件中同时存在确定型共因事件,可通过将相应条件失效概率值设置为1来表征确定型CCF。模型对多个共因事件没有独立性要求,模型规模可控、构建方法简洁。

实际工程应用中存在许多复杂系统,PMS-BN模型中网络节点的数量会随着系统复杂度的增加成倍上升,为建模带来困难。当系统任务的阶段数、元件数较多,难以构建完整的PMS-BN模型时,可以依据系统任务的实际情况,判别共因事件可能发生的任务阶段及影响层级,在系统中选取适当的层级或可能受到CCF影响的部分阶段来应用PCCF-PMS模型进行分析。

网络参数的确定需要与CCF相关的一系列原始数据支撑,如共因事件发生概率、元件在共因事件影响下的失效概率、各共因事件间的统计关系等。在实际应用中,相关数据可能难以获取或是基于分析人员工程经验,因此,后续研究工作将重点关注在不确定性情况下受CCF影响的PMS可靠性分析方法。