局部通信条件下多无人机协同搜索方法
2022-11-19朱晓敏刘大千费博雯
朱晓敏, 刘大千, 费博雯, 门 通
(国防科技大学系统工程学院, 湖南 长沙 410073)
0 引 言
近些年,随着人工智能、机器视觉技术的兴起,无人目标搜索成为智能无人系统研究领域的热点问题之一,在军事和民用领域均得到了广泛的应用[1-3]。然而,由于受视野、能耗等限制,单无人机难以适应复杂多变的恶劣环境,因此多机协同成为必然选择[4],利用共享视野、协同定位等技术,有效地执行难度更高、更复杂的目标搜索任务。
复杂未知环境下的多无人机协同搜索研究是近年来研究的热点,国内外专家学者针对概率图、飞行避障、群智能优化决策等方面均取得了一定的成果。在概率图方面,Yu等人[5]使用目标概率图(target probability map, TPM)来描述目标存在于任务区域中特定位置的可能性,并建立了基于概率的搜索动态已知目标的决策方法。吴岸平等人[6]提出了不确定环境下无人机区域目标搜索方法,并建立了基于二维离散网格的无人机区域搜索模型,采用概率地图描述目标信息的实时获取与更新,通过使用蒙特卡罗方法验证了区域搜索方法的有效性。杨春宁等人[7]提出未知区域无人机协同搜索方法,该方法实现了对未知区域的搜索覆盖面积和搜索时间的优化部署,并基于概率地图信息更新融合的协同搜索策略,实现了无人机自主协同控制。刘重等人[8]提出了基于信息素回访的目标搜索方法,建立包含目标存在概率地图、不确定地图和数字信息素地图在内的环境感知地图,并在此基础上设计了协同搜索决策方法。黄杰等人[9]提出了基于双属性概率图的搜索方法,建立了基于收益函数的协同模型,并利用遗传算法进行优化求解,实验结果验证了该方法的协同有效性及目标搜索能力。然而,由于目标是运动的且方向未知,利用传统的信息概率图进行匀速搜索,显然无法满足现实需求,存在目标搜索遗漏和搜索周期较长等问题。
在飞行避障方面,Bo等人[10]提出了一种具有避障约束的路径规划模型,并通过分散模型预测控制建立了一种轨迹规划策略来寻找最优解。为了克服任务分配与路径规划之间的信息耦合所带来的困难,Yao等人[11]设计了一个分布式任务规划框架,有效地控制了任务评估误差,用较少的计算资源获得了较优的结果。Radmanesh等人[12]设计了一种基于偏微分方程的分散式无人机三维轨迹生成方法,并选取3架无人机进行了实验验证。Yang等人[13]针对静态环境的避障问题,提出了一种适用于小型无人平台的Dubins曲线避障路径规划算法。Song等人[14]提出了一种基于Dubins路径的A*算法,为智能无人平台在避障和转弯半径约束下,规划可行飞行路径。上述方法在相对单一环境中均取得了理想的效果。然而,当搜索环境中包含密集建筑时,约束条件不断增多,易造成算法的求解复杂度增高,进而影响目标搜索效率。
在群智能优化决策方面,Carabaza等人[15]提出了一种基于蚁群优化(ant colony optimization, ACO)算法的无人机轨迹生成方法。在具有不同特征的搜索场景下,可以获得高质量、高水平的无人机直段弹道。考虑到实时路径规划问题,Huang等人[16]提出了一种基于k次平滑的多无人机协调路径规划方法,该方法采用改进的蚁群优化算法来获得更具可飞性的路径。Zhu等人[17]提出了一种基于博弈论的分布式接入点选择算法,利用该算法指导用户自主选择基站或无人机作为接入点,并采用基于深度强化学习的方法求解无人机路径规划子问题,指导无人机在每个位置采取最优的行动。Li等人[18]以森林火灾预警监测为背景,研究了扫描覆盖中的最小时间最大覆盖问题,并提出了一种考虑目标权重和无人机性能约束的启发式算法,利用加权目标扫描覆盖来寻找最优路径。Yao等人[19]提出了一种基于模型预测控制和灰狼优化算法的混合方法,以控制方法为框架实时获取无人机的轨迹,优化跟踪性能。然而,这些方法均使用全局优化策略,未考虑通信链路失效的问题,一旦全局信息无法共享,即无人机群无法保障实时位置共享,易造成优化策略的失效,导致多机目标搜索准确率的降低。
综上所述,现有的目标搜索方法能在一定程度上解决通信链路稳定条件下的多无人机协同搜索问题。然而,在一些复杂环境中,仍然存在以下问题急需解决:① 由于建筑物等障碍物的干扰,而导致无人机编队的通信链路不可达问题;② 在复杂环境中,特别是建筑物密集的情况下,目标搜索遗漏、搜索周期较长等问题。针对上述问题,本文提出了局部通信条件下的协同搜索(cooperative search under local communication, CSLC)方法。在现有数字信息概率图的基础上,构建当前时刻无人机编队的通信拓扑结构,并构建基于通信链路稳定收益和协同编队收益的协同搜索模型。与此同时,为了满足目标动态变化下的搜索问题,本文设定各无人机做变速运动,且加入最大运动速率约束以及安全飞行约束,从而保证模型能够得到最优路径可行解,提高了多无人机协同搜索效率。
本文的创新之处如下:
(1) 提出CSLC方法,解决全局通信链路不可达下的搜索效率低的问题;
(2) 针对目标高度动态变化问题,提出基于无人机变速运动的协同优化模型,提高方法的协同搜索能力;
(3) 在模型求解过程中,建立了安全距离和最大运动速率的约束,保证模型能够得到最优路径可行解。
1 问题描述
在未知目标区域Ω中,利用N架无人机搜索M个运动目标,每架无人机均搭载垂直向下的图像探测器用于发现目标。由于探测器的检测范围限制,为了保证目标识别的准确率,本文假设仅当目标位于传感器图像的中央区域时,认定该架无人机能够准确发现目标,即当无人机飞行到目标的正上方时,认定该目标能够被精准识别。
1.1 搜索区域模型
为了清晰地描述无人机协同搜索路径,本文简化搜索区域模型的解空间,对区域Ω进行栅格化处理,具体的栅格化地图如图1所示。假设目标区域Ω的长和宽分别为X和Y,将Ω等分为若干个大小为Δx×Δy的矩形网格。需要指出的是,Δx与Δy在选值上需小于无人机探测图像的内接矩形,确保无人机能够准确识别该区域内的目标。
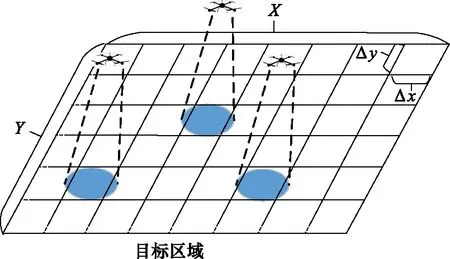
图1 多无人机协同目标搜索场景
1.2 无人机模型
假设每个网格最多只有一个目标,无人机利用图像探测器对每个网格区域进行搜索,其飞行路线受转弯半径和速度的约束[20],因此飞行状态可表示为
UAVi(t)=[xi(t),yi(t),di(t)]
(1)
式中:xi(t)为第t时刻目标区域横坐标方向的位置坐标;yi(t)为纵坐标方向的坐标;di(t)为无人机行进方向。在基于网格的飞行过程中,认为无人机从第t时刻到第t+1时刻可有5个方向选择,分别为:① 向左90°;② 向左45°;③ 向前;④ 向右45°;⑤ 向右90°,即无人机偏航角增量为Δd∈[-2,-1,0,1,2](-2表示向左90°,-1表示向左45°,以此类推)。若采用图2中的八链码方向表示无人机行进方向,则无人机运动模型为

图2 八链码与偏航角增量
(2)
式中:v为无人机飞行速度;θ为无人机偏航角,θ∈[-90°,45°,0°,45°,90°]。
2 CSLC建模
现有的目标搜索方法多假设无人机编队的通信链路是时刻畅通的,然而在实际飞行过程中,建筑物等障碍物会严重影响无人机编队的通信网络。一旦无法进行全局通信,则编队跟踪易成为“单打独斗”,失去了多平台协同搜索的优势,因此本文首先建立当前时刻无人机编队的通信拓扑关系,具体示意如图3所示。在此基础上,设计了基于通信链路稳定收益和协同编队收益的搜索模型,在当前网络通畅的条件下达到局部位置信息共享,并不断联络其他无人机,从而将多平台的协同效率最大化,具体模型描述如下。

图3 局部互通网络
图3中,蓝色圆圈代表每个无人机,黑色虚线框和实线矩形框分别代表网格和建筑物。假设r为通信阈值(图1中,r=3),当前时刻存在两个局部互通网络,UAV1、UAV2和UAV3为网络1,UAV4与UAV5为网络2。其中,UAV2和UAV3是通过UAV1间接通信。
2.1 通信拓扑关系
在实际的飞行过程中,无人机之间的通信网络受相对距离的影响,因此本文利用有向图G=
(3)
式中:r为通信阈值;N为无人机数量。由此可以看出,邻接通信矩阵A能够清晰表达各无人机之间的实时通信拓扑关系,若aij=1,则表明此时无人机i与无人机j联通,能够互发位置等信息。因此,该无人机编队的整体通信拓扑矩阵(有向图的可达矩阵)为
C=A⊕A2⊕…⊕AN
(4)
式中:⊕为求和操作。因此,矩阵C表示当前时刻无人机编队的实时通信拓扑关系。本文以4架无人机为例,对通信拓扑矩阵C进行算例说明。假设当前时刻的邻接通信矩阵A为

(5)
则
(6)
(7)
(8)
(9)
将式(9)中不为0的元素变为1,则矩阵C可表示为

(10)
由式(10)的通信拓扑矩阵可以看出,当前时刻由4架无人机组成的编队满足全联通条件,即满足全局通信条件。
2.2 协同搜索目标函数
综合考虑无人机通信能力和编队协同搜索能力,本文将通信链路稳定收益和协同编队收益作为目标函数,计算搜索模型的最优解,这两种收益的具体描述如下。
(1) 协同编队收益
为了保证无人机编队协同编队搜索的收益,本文引入数字信息素策略[21-22],将各个网格给定不同的信息素值,从而构造面向未知环境的人工势场。各无人机利用现有的通信拓扑关系进行协同路径规划,并利用实时位置信息更新各网格的信息素值。局部通信下的协同编队收益可表示为
(11)
式中:n为预测步长;sa表示在当前通信网络中第t时刻无人机位置的吸引信息素强度;sr表示当前时刻无人机位置的排斥信息素强度;α和β为权重系数;e(1-i)/n∈(0,1]为动态收益系数。考虑到预测步长越大,信息素强度的准确性越低,采用动态收益系数能够平衡对编队收益准确性的影响。
(2) 通信链路稳定收益
在协同目标搜索过程中,由于无人机的通信能力限制,特别是在较为复杂的环境中,飞行障碍、建筑物遮挡等因素都会严重影响无人机的通信效果。因此,本文研究的目标是使每架无人机均能最大概率发现搜索目标的同时,最大化编队通信链路的传输稳定性,从而保证协同目标搜索的效率。假设无人机分布在同一高度,且初始坐标已知,单无人机在时间t的信息传输稳定性为
(12)
(13)
式中:si表示无人机之间的最大传输距离。相应地,无人机编队的通信链路稳定收益为
(14)
2.3 飞行约束条件
(1) 安全距离约束
在多无人机协同规划过程中,由于无人机分布在同一高度,一旦编队飞行距离不受限制,多无人机之间就有发生碰撞的风险。为了避免这个问题,须确保无人机之间保持一定的安全距离[23-24]。为了简化多架无人机之间安全距离的统计过程,本文为编队中的每架无人机提供一个编号,并按升序依次计算与无人机之间的距离。固有约束表示如下:

(15)
式中:dsafe是一个常数,表示无人机的最小安全距离。
(2) 运动速率约束
现有多无人机协同搜索方法主要基于以下两点假设:① 目标的运动轨迹已知;② 目标与无人机均匀速运动。然而,在未知环境中,存在大量动态、随机性因素。例如,由于速度和方向的时刻变化,目标的运动轨迹无法准确预测。因此,设定目标的运动轨迹未知,且无人机做变速运动,本文利用固定常量限制的方式对无人机的运动速度进行约束,具体表达式为
(16)
式中:smax表示无人机的最大运动位移。
2.4 模型求解
在目标搜索过程中,由于通信距离的限制,导致无人机编队无法实时全局通信,因此本文建立基于局部通信的协同搜索模型,具体表达式为

(17)
式中:λ1和λ2为归一化系数i=1,2,…,N-1;k=i-1,i,…,N。由于式(17)的目标函数包括二次项,本文利用Kuhn-Tucker条件将模型降为线性规划问题进行求解,获得各无人机的最优航迹规划位置。
2.5 算法流程
本文利用基于二次项的协同方法遂行目标搜索任务,该方法的主要流程如图4所示,具体算法步骤如下。

图4 协同目标搜索流程
步骤 1设置初始参数包括无人机数量N,目标数量NT,数字信息素预测步长n,各无人机的初始位置以及初始航向角。
步骤 2设置初始数字信息素参数。吸引信息素:挥发系数Ga,传播系数Ea,释放常量Da。排斥信息素:挥发系数Gr,传播系数Er,释放常量Dr。
步骤 3计算各无人机间的欧氏距离,利用式(4)生成第t时刻编队的局部通信网络组成。
步骤 4基于通信拓扑矩阵的结构,对各局域网下多无人机协同搜索模型求解:
步骤 4.1当无人机间的距离均大于阈值时,各无人机按照式(2)生成各自的飞行路径;
步骤 4.2当两个以上的无人机满足距离约束时,利用式(16)计算该网络下无人机协同目标搜索模型。
步骤 5判断是否满足最大搜索时长,若满足,则输出最优航向路线;若不满足,则令t=t+1,转至步骤4。
3 实验结果与分析
在本文实验中,首先,对实验中的一些重要参数进行说明,然后设置了几组与现有方法的对比仿真实验,从定性和定量两个方面验证提出的协同搜索方法的有效性。
3.1 实验参数设置
搜索任务区域Ω的大小为3 050 m×3 050 m,并划分为61×61个网格,每个方格的边长为50 m。在该任务区域中,设置了许多楼宇等规则建筑物,模拟复杂的城市环境。每个建筑物占用3×3个网格。数字信息素[25]是计算搜索模型的协同编队收益的重要指标,是本文的重要组成部分之一,其主要初始参数设置如表1所示。初始无人机编队和目标数量分别设置为12架和9个,无人机与目标的初始参数设置如表2和表3所示。

表1 数字信息素初始参数

表2 无人机初始状态

表3 目标初始状态
3.2 对比仿真实验
为了验证本文提出方法的有效性,本节主要将CSLC与文献[25]的分布式模型预测控制 (distributed model predictive control, DMPC),文献[26]的基于遗传算法的信息素图谱 (pheromone map based on genetic algorithm, PMGA) 两种方法进行仿真对比,考察发现目标数、路径覆盖率、搜索迭代周期等主要指标[27-30],分析两种方法的优越性。DMPC方法是基于贝叶斯理论对目标的运动状态进行估计,并设计了带有调度信息素的数字信息素图方法,保证了多无人机协同搜索目标的能力。PMGA方法根据覆盖给定面积百分比所需的距离进行评估,设计了一种基于遗传算法的信息素映射方法,用于无人机编队的飞行路径规划,提高了协同搜索的有效性。
(1) 搜索路径对比
CSLC、DMPC与PMGA 3种方法在不同迭代周期下的搜索飞行路径如图5~图7所示。其中,图5为3种方法在100个搜索周期下的飞行路径图,图6为在200个搜索周期下的飞行路径图,图7为300个搜索周期下的飞行路径图。图中,不同颜色的虚线表示各无人机的飞行路径,而不同颜色的实线则表示目标的运动路径。

图5 3种方法在100个周期下的的搜索路径对比

图6 3种方法在200个周期下的的搜索路径对比
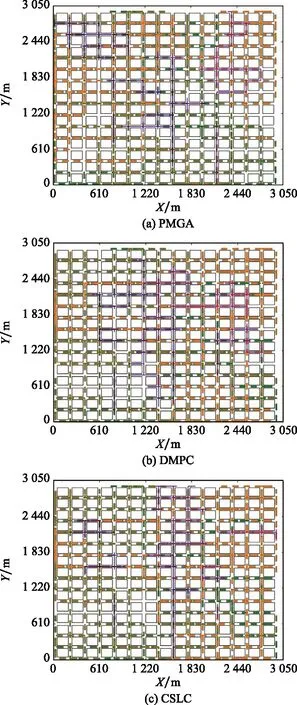
图7 3种方法在300个周期下的的搜索路径
无人机和目标的初始位置如表2和表3所示,DMPC与PMGA为全局网络通信,而所提的CSLC则为局部通信,通信阈值r设置为20个网格。相应地,3种方法在发现目标数以及路径覆盖率方面的定量对比如表4所示。

表4 3种方法的实验数据对比
图5~图7清晰地显示了3种方法在不同迭代周期下的飞行路径俯视图,可以看出,本文提出的CSLC方法能够更加合理的对目标区域进行覆盖式搜索,保证了多无机协同搜索目标的能力。为了进一步说明本文方法的有效性,表4列出了3种方法在不同周期下的目标识别数和区域覆盖率对比结果。
周期在100 s时,3种方法的目标识别数较少,均小于目标总数的一半,这是因为目标区域过大,由于初始化目标与无人机之间的距离较远,因此在有限时间内无人机的发现目标数较少。随着搜索时间的不断延伸,本文提出的CSLC方法体现出了变步长搜索的优势,无论是在目标识别数方面或在区域覆盖率方面均优于DMPC和PMGA方法,证明了本文提出的CSLC方法搜索策略的有效性。
(2) 内置参数对搜索算法的影响
1) 通信阈值对搜索结果的影响
本节主要分析通信阈值对本文提出的CSLC方法的影响,因此分别设置无人机编队间的通信阈值为10个网格、20个网格、30个网格以及40个网格,统计不同网格情况下的目标搜索性能。CSLC方法在不同通信阈值下的通信网络个数如图8所示。相应的,该方法在不同通信阈值条件下的目标识别个数和搜索区域覆盖率如表5所示。
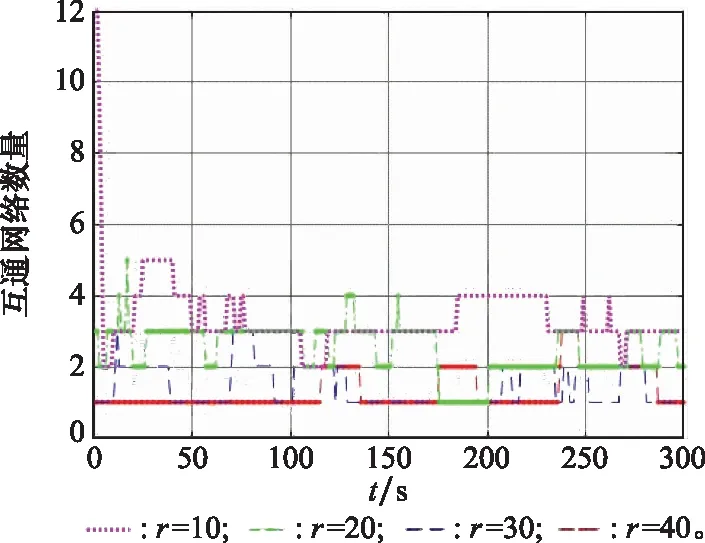
图8 不同阈值条件下的局部网络数量

表5 不同阈值条件下的实验结果对比
从图8可以看出,在通信阈值r=10时,无人机编队中的局部网络数量较多。然而,随着阈值的不断增加,编队中的网络数量随之减少,即编队中的无人机均能直接或间接的通信,共享彼此的位置信息,从而保证搜索任务的高效完成。与之对应的,在表5中,当r=10时,编队的目标搜索数量只有6个,无法满足任务的需要,且区域覆盖率仅有72.36%。然而在r=40时,无人机编队在第200个迭代周期中能够搜索到8个目标,且区域覆盖率与r=20时相当。在对比r=20,r=30和r=40的过程中,不难发现,3种方法虽然在网络数量上有所不同,但最终都能够完成对所有目标的搜索,且区域覆盖率相差不大,这说明了CSLC方法对通信阈值并不十分敏感,其中设计的策略具有一定的搜索稳定性。
2) 无人机数量对搜索结果的影响
为了进一步分析本文方法的效能,本节主要分析无人机编队数量对目标搜索结果的影响。首先选取目标的数量固定为9个,然后设定搜索编队中无人机的数量为8、12、16、20架时分别进行4组仿真实验,搜索迭代周期设置为200 s,评价指标为无人机发现目标数。为了实验对比的公平性,本文每组实验分别进行10次,统计出每组实验的平均完成值,DMPC、PMGA和CSLC 3种方法的具体指标值如图9所示。

图9 不同无人机数量下的发现目标对比
在每次实验中,无人机的初始位置分布均在目标区域的四周进行随机初始化生成的。从图9可以看出,随着无人机数量的增多,3种方法的发现目标数量也随之增加,这也进一步证明了3种方法协同搜索的有效性。由于无人机数量的不断增多,在限定的时间内被探测的网格也将随之增多,即目标区域中有更多的网格被无人机编队搜索,因此目标发现数量将随之增加。与此同时,根据数据的对比,CSLC方法的搜索性能要明显高于DMPC和PMGA两种方法,这进一步证明了本文方法的目标搜索能力。
3) 无人机探测半径对搜索结果的影响
无人机探测半径是协同目标搜索任务中的重要一环,决定着目标搜索任务的成败。本节选取目标的数量仍为9个,无人机的数量为12架,初始位置分布如表1所示,迭代周期设置为200 s。设定探测半径分别为1、4、9个网格,评价指标为无人机发现目标数,并每组实验分别进行20次取平均值,具体指标值如图10所示。

图10 不同网格数下的发现目标数
从图10可以看出,随着传感器探测面积的增大,两种方法的平均目标发现数量也随之增加。由于传感器探测面积的不断增大,导致每一时刻各无人机的搜索区域将随之增多,即目标区域中有更多的网格能够被探测,因此发现目标数量应明显增加。本文将目标区域布置了密集的建筑物,导致两种方法的检测结果只是略有增加,但这也能够证明CSLC的协同搜索模型的有效性。
4 结 论
本文针对复杂环境下多无人机协同目标搜索问题进行了研究与分析,提出了局部通信条件下的搜索模型,建立了包含编队通信拓扑结构关系以及编队收益函数在内的多个优化指标。同时,在求解的过程中加入编队飞行所需的限制条件。实验结果表明,与当前流行的搜索方法相比,在同等搜索周期下,本文提出的CSLC方法无论在区域覆盖率方面,还是在目标识别数量上均优于其他算法。与此同时,为进一步验证CSLC的搜索效率,随机增加无人机数量以及各无人机的探测网格数,实验验证了本文在通信条件受限的情况下均能达到较高的搜索目标数,从而说明CSLC方法能够有效提高搜索系统的协同性,具有较高的搜索覆盖率和发现目标数。
