基于深度字典学习的输电线路故障分类方法

2022-11-19张宇博郝治国林泽暄杨松浩刘志远于晓军

电力自动化设备 2022年11期

张宇博，郝治国，林泽暄，杨松浩，刘志远，于晓军

（1. 西安交通大学电气工程学院，陕西西安 710049；2. 国网宁夏电力有限公司，宁夏银川 750001）

0 引言

电力系统中输电线路运行环境复杂，易受各种人为或自然因素影响而发生故障。在线路故障后快速、准确地识别故障类型，对于提高故障定位精度、缩短故障线路恢复运行时间、提高电力系统稳定性等具有重要意义。

已有的输电线路故障分类方法大致可分为基于物理模型的方法［1-3］和基于数据驱动的方法［4-10］。基于物理模型的输电线路故障分类方法通过构建输电线路的物理模型，对输电线路不同故障类型之间的差异进行解析，设计指标并选取阈值，实现故障类型的判别，具有物理意义明确、易于微机实现的优点，但也存在一定的局限性，例如：文献［1-2］基于输电线路的故障稳态模型判别故障类型，但故障前后系统参数的变化对方法的准确性影响较大；文献［3］基于输电线路故障暂态模型方法的准确性受故障条件的影响较大，且对采样率等硬件条件要求较高。基于数据驱动的输电线路故障分类方法借助大数据、人工智能等技术，从样本中自动提取故障特征，避免了复杂的物理建模过程和繁琐的阈值整定过程，例如：文献［4］利用滤波后的三相电流振幅作为故障电流特征，并将其输入支持向量机SVM（Support Vector Machine）实现故障分类；文献［5］将小波分析与经人工神经网络ANN（Artificial Neural Network）改良的粒子群优化PSO（Particle Swarm Optimization）算法结合来实现输电线路故障分类。这些基于传统人工智能的故障分类方法，设计流程相对简单，但在故障特征提取、小波选型等方面，仍部分依赖人为参与［11］。近年来，深度学习以其强大的非线性映射和特征提取能力得到了广泛的应用并且效果显著［12］。目前已有研究将深度学习技术应用于输电线路故障分类问题并取得了一定成果。例如：文献［6］将自编码器SAE（Sparse AutoEncoder）与卷积神经网络CNN（Convolutional Neural Network）结合实现交流系统输电线路的故障分类问题；文献［7］利用并联卷积神经网络P-CNN（Parallel Convolutional Neural Network）快速检测直流输电线路的故障类别和故障支路。同样地，在小电流接地系统的故障选相问题中，深度学习的有效性也得以验证［8-9］。但是深度学习模型是典型的黑箱算法，模型复杂，且所得特征缺乏可解释性。

稀疏表示与深度学习类似，都属于以数据驱动特征自动提取的方法。与深度学习不同的是，稀疏表示理论以字典原子的线性组合来重建信号，所提取的字典原子与信号本身是线性关系，具有较好的实际意义，符合人的直观认识。文献［10］对稀疏表示用于输电线路故障分类问题进行了初步探索，但是模型相对简单，且直接以故障样本组成字典，缺少了对故障样本特征的挖掘和学习过程，字典原子缺乏代表性。

本文基于稀疏表示理论，借鉴深度学习的逐层提取特征的思想，提出了一种可用于输电线路故障类型识别的深度字典学习模型。该模型利用稀疏性约束逐层学习故障数据中的典型结构特征，构成深度故障字典，最后根据故障样本的重建误差确定其所属类别。该方法无须人为提取故障特征，且模型学习到的特征符合人对故障的直观认识，一定程度上解决了故障特征的可解释性问题。大量仿真数据验证了本文所提方法具有较好的鲁棒性和泛化能力。

1 稀疏表示理论与深度字典学习模型

1.1 稀疏表示理论

稀疏表示就是使用少量基本信号的线性组合表示目标信号，通过“稀疏性”这一强制要求提取目标信号中的关键信息，从而实现信号的压缩和特征提取。其数学模型如式（1）所示。

式中：y为目标信号（样本），y∈Rn×1，n为样本维度；D∈Rn×M为基本信号矩阵，M为基本信号数量；x∈RM×1为目标信号y在基本信号矩阵D下分解的系数向量且要求其是稀疏的；r∈Rn×1为残差向量。

基本信号矩阵又被称为字典，每个基本信号都是一个字典原子，因此字典D可表示为：

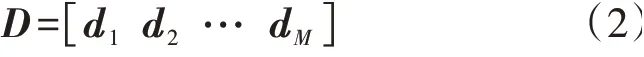
式中：di∈Rn×1，i=1，2，…，M。

字典的构造是稀疏表示理论的关键，根据构造方法的不同可分为解析方法和学习方法2 种［13］。解析方法中字典是利用某种数学变换构造得到的，如离散余弦变换、小波变换等［14］，然后在预定义字典上寻求目标信号的稀疏表示。学习方法中字典是根据样本数据的特点自适应学习得到的，即字典原子可以根据样本和待求解问题的特点灵活调整。与解析方法相比，学习方法的字典原子形态更丰富，针对性更强，能更好地与样本内含的结构相匹配。因此，本文使用学习方法构造故障字典。

1.2 基于学习方法的字典构造

如1.1节所述，学习字典的构造依赖于研究的问题及样本数据的特点。具体地，结合式（1）可知，基于学习方法构造字典的实质就是求解特定的矩阵D使其在满足一定的稀疏性约束条件下使样本数据的表示误差最小。因此，学习方法中字典的构造可以转换为求解如式（3）所示的约束优化问题。

由于存在2个未定矩阵变量D和X，直接求解式（3）是一个NP-hard 问题［15］，因此一般采用交替迭代进行求解：先固定字典D求解系数矩阵X（此时D为已知量），然后利用求解得到的稀疏矩阵X对字典D进行更新（此时X为已知量），重复上述操作直至误差满足要求或达到最大迭代次数。

已知字典D求解系数矩阵X是一个标准的编码问题，利用正交匹配追踪OMP（Orthogonal Matching Pursuit）［16］算法可以快速求解。OMP 算法的核心思想是：以贪婪迭代的方法选择字典D中的原子，使得在每次迭代的过程中所选择的字典原子与当前残差向量相关性最大，从原始信号向量中减去相关部分并反复迭代，直到迭代次数达到预设稀疏度。算法实现如附录A图A1所示。

固定系数矩阵X更新字典D是学习字典模型中的关键步骤，其中应用较为广泛的有最优方向法MOD（Method of Optimal Directions）［17］、K-奇异值分解法K-SVD（K-Singular Value Decomposition）［18］、序列泛化K 均值SGK（Sequential Generalization ofK-means）［19］等算法。考虑到SGK算法能够逐原子更新，与SVD 等其他算法相比复杂度更低，计算高效且对硬件资源占用更少，本文利用SGK 算法实现字典D的更新，具体如式（4）所示。

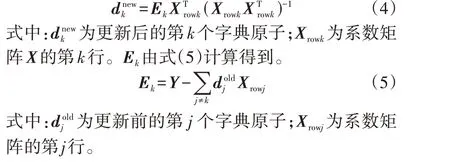
1.3 深度字典学习模型

传统的基于学习方法构造的字典是单层结构且以残差为驱动，当稀疏性指标大于1 时，学习到的字典原子将由反映样本的轮廓特征向反映样本的细节特征转变，如附录A 图A2 所示。由式（4）所示的字典原子更新算法可知，这种单层字典结构使得反映样本不同特征尺度的字典原子之间相互影响，削弱了字典原子的泛化性能。进一步地，当字典中存在多个样本非常相似且稀疏性指标大于1 时，OMP 算法可能会得到错误的重构信号，从而影响方法的有效性和准确性［20］。

考虑到传统学习方法的局限性，本文借鉴深度学习理论中的逐层特征提取思想，采用字典层数替代稀疏性指标，构建深度字典，即将单层多稀疏度结构转换成为多层单稀疏度结构。具体地，构建一个s层的字典（s对应传统学习方法中的稀疏度指标），各层字典的稀疏度s′均为1，以信号的表示残差逐层驱动字典学习，其原理如附录A 图A3所示。采用多层字典结构保证了不同特征尺度的原子彼此独立、互不影响，同时单稀疏度结构避免了OMP 算法可能出现的重构错误问题。

2 基于深度字典学习模型的故障分类算法

输电线路故障类型判别本质上是一个样本分类问题，利用深度字典学习模型解决分类问题时，主要由以下2个步骤构成：

1）深度故障字典的构建，即首先生成带类别标签的样本库，然后利用1.3节所述的深度字典学习模型按类构建深度故障字典；

2）故障样本分类的实现，即将各类故障字典的同层合并，然后基于合并后的深度故障字典对待分类样本进行稀疏表示，利用稀疏系数对样本按类重构，重构误差最小的类别就是样本所属类别。

2.1 输电线路故障样本库

本文以电流信号作为故障类型判别的关键信息，具体地，利用故障前后一段时间内的各相电流和零序电流值按顺序拼接并归一化形成故障样本。考虑到一般断路器的动作时间为0.06～0.15 s［21］，为保证方法的有效性，取故障前1个工频周期和故障后3个工频周期的数据为有效数据，归一化方法如式（6）所示，某A相接地故障样本示例如附录A图A4所示。

式中：i为原始故障样本；i*为归一化故障样本。

输电线路故障类型有单相接地故障（Ag，Bg，Cg）、相间短路故障（AB，AC，BC）、两相短路接地故障（ABg，ACg，BCg）和三相短路故障（ABC），共计10种故障类型。则样本矩阵按上述分类顺序可表示为：

2.2 按类构建深度故障字典

1.3 节给出了深度字典学习模型的求解原理和一般形式，现将其扩展到求解多类问题上并给出其详细的求解过程。

由于各故障类型对应的样本库相互独立，故可对故障类别进行解耦，即由2.1节构建的各类样本库Yi独立导出各类别对应的深度故障字典Di。由于各子类深度故障字典的求解过程完全相同，下面以类别i为例给出深度故障字典的具体求解过程。

基于图A3所示的求解原理可知，各子层字典的求解过程彼此独立，以残差作为驱动，可采用串行递推的思路逐层进行求解。具体地，参照式（3），第j层的求解过程可表示为如式（8）所示的数学模型。

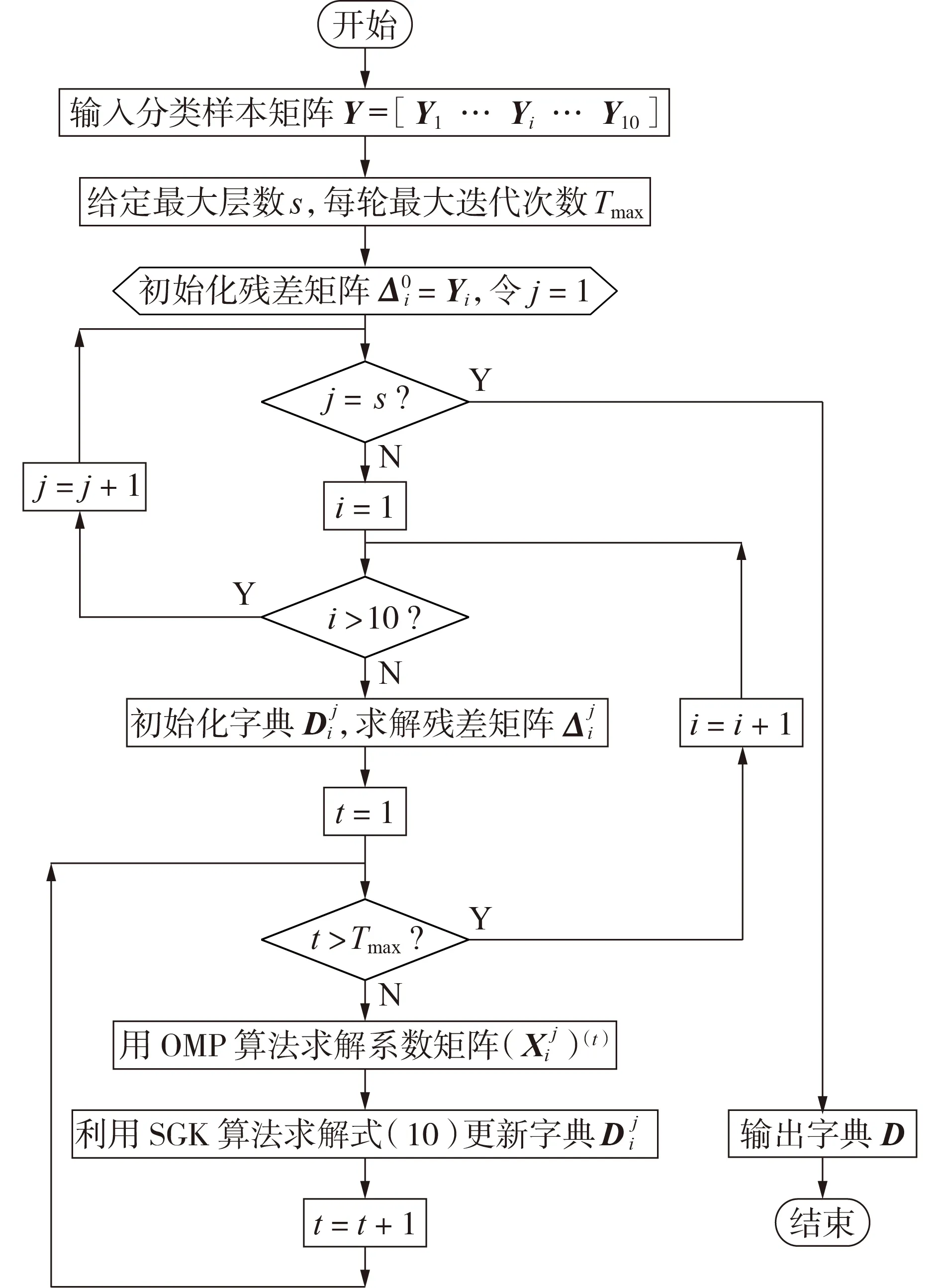
图1 按类别构建深度故障字典流程图Fig.1 Flowchart of constructing multiclass deep fault dictionary

2.3 故障分类

将上述按类别学习得到的深度故障字典用于故障样本的分类时，其基本思想就是在满足一定稀疏性约束的条件下，利用该含有类别信息的深度故障字典中原子的线性组合来表示待分类样本y。其数学实质就是在已知字典时，求解待分类样本的深度稀疏表示，根据稀疏表示系数在类间的分布信息判定样本所属类别。样本深度稀疏表示的数学模型为：

根据前文所述，在字典已知的情况下，利用OMP 算法可以快速求解式（11）所示的约束优化问题，即以残差为驱动，通过OMP 算法可串行递推待分类样本在各层字典上的系数向量，实现对待分类样本的深度稀疏表示。具体地，由式（11）的约束条件可知每层字典的稀疏度为1，利用图A1 所示的OMP 算法求解稀疏度为1的样本稀疏系数向量即为求解与残差向量最为接近的字典原子及其表示系数。各层稀疏系数的求解是彼此独立的，即重复求解稀疏度为1 的OMP 算法，以残差为驱动串联各层字典，上一层的残差作为下一层的目标信号，详细求解过程见附录A图A5。

最后，根据系数向量按类别进行信号重构，重构误差最小的类别就是该样本所属的类别，判别方法如式（13）所示。

3 仿真验证

3.1 故障样本库的生成

本文利用PSCAD／EMTDC 软件搭建双端电源模型进行仿真获取大量故障样本，故障仿真模型如图2 所示，系统电压为220 kV，频率为50 Hz，输电线路长度为80 km，采样频率设置为2 kHz，线路参数参照文献［6］进行设置。

图2 双端电源系统故障仿真模型Fig.2 Fault simulation model of dual-terminal power system

为尽可能多地获取故障仿真数据，提高模型的准确性，本文将各种可能的故障条件进行组合，故障条件设置如表1 所示，共计得到5 280 份故障仿真数据，每种故障类型包含528 份样本数据，按2.1 节中所述方法，生成故障样本库Y。

表1 故障条件设置Table 1 Settings of fault conditions

对于任一待分类样本y，其构建过程与2.1 节中样本的构建过程相同。具体地，提取输电线路故障前一周期和故障后3 个周期的三相电流和零序电流的采样值，按顺序拼接并进行归一化操作，即待分类样本y可表示为：

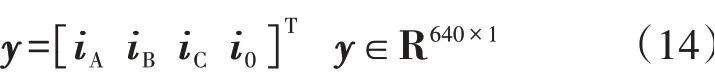
式中：iA、iB、iC为归一化的三相电流采样值，i0为归一化的零序电流采样值，且iA，iB，iC，i0∈R1×160。

3.2 构建深度故障字典

代价函数J的大小可以衡量模型的性能，J值越小，表示模型误差越小，模型性能越好。下面以代价函数J为指标，讨论字典初始化方法、字典规模以及层数等关键超参数对模型性能的影响。

3.2.1 字典的初始化方法

3.2.2 字典的规模

字典的规模也是影响模型性能的重要因素，应综合考虑模型性能和求解代价，选择合理的字典规模和层数，在保证模型性能的前提下尽可能缩短模型训练时间、减少对硬件资源的占用。

在［0.1，0.5］范围内，从0.1 开始每隔0.05 取1 个值作为字典中原子总数占总样本总数的比例，并设置字典层数为1—8 层，在上述设置下进行迭代求解，不同组合下模型最终的代价函数取值如附录A图A7 所示。图中：rs为字典中原子总数占样本总数的比例。由图可见，当字典规模和层数增加到一定程度时，模型性能趋于稳定，此时继续增加字典规模和层数对模型性能的提升作用不大。因此本文最终选定字典层数为5 层，即s=5，字典中原子总数占样本总数的比例为0.3，则每类别每层字典中有31个字典原子(5 280×0.3/(10×5)=31)。

3.3 分类效果及鲁棒性验证

由式（13）可知，根据待分类样本y在深度字典D中的分解系数对样本y按类进行重构，重构误差最小的类别就是本文方法判别的y所属的类别。因此，对比样本y在各个类别下的重构误差也可有效衡量方法的有效性，即样本y实际所属类别的重构误差越小、非所属类别的重构误差越大，则方法的性能越好。定义2 个评价指标eii和eik(i≠k)以定量描述这一特性，如式（16）所示。

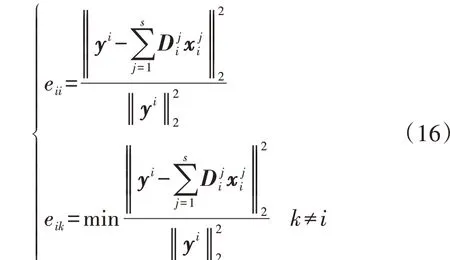
式中：yi表示样本y实际属于类别i；eii为第i类字典的重构误差；eik为其他类字典重构误差的最小值。若eii越接近0、eik越接近1，则表明样本y能够越好地用其实际所属类别的字典原子进行表达，分类效果越好。

重构误差指标eii和eik反映了单个样本的分类效果，进一步地，定义如式（17）所示的重构误差均值指标和来衡量所提方法在样本集上的整体表现。

基于2.3节给出的故障分类算法，利用故障样本库Y验证深度故障字典D的分类效果，结果表明算法能准确识别出全部样本所属的类别，分类正确率为100%。同时，基于式（17）中的重构误差均值指标，得到本文所提方法在识别样本库Y中各类故障的性能表现如图3所示。

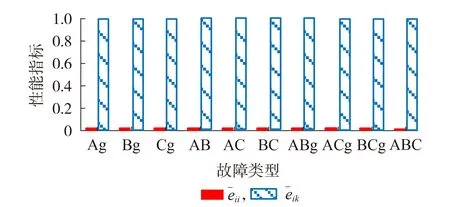
图3 重构误差均值指标对比Fig.3 Comparison of average indicators of reconstruction error

从图3 可见，所提方法在保证正确分类的前提下，重构误差均值指标接近于0接近于1，表明样本集中的样本可以很好得由其所属类别的字典原子表达，证明了所学习到的深度字典的有效性。同时，0和1的对比表明所提分类指标具有较高的容错裕度和鲁棒性。

考虑到实际运行环境中存在噪声，本文对所提方法的抗噪性能进行了验证，利用MATLAB 对样本库Y中全部5 280 份故障样本添加高斯白噪声，然后利用深度故障字典D对含有噪声的故障样本进行分类，不同噪声强度下本文所提方法和文献［10］所提方法的分类正确率和所有样本的重构误差均值指标对比结果如表2 所示。由表可见，本文所提模型在各种噪声强度下均可以实现正确分类，且对样本的重构误差均值受噪声强度的影响很小，和之间差异显著，证明了该模型具有较好的抗噪性能。而文献［10］所提方法的分类正确率随着噪声强度的增大而减小，且重构误差均值指标和之间的差异显著小于本文所提方法。

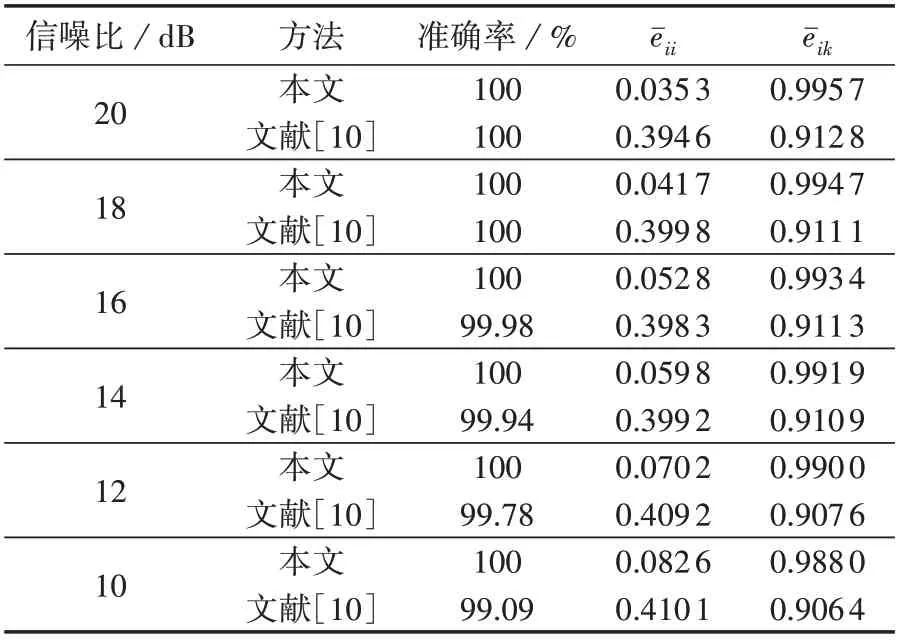
表2 2种方法的抗噪性能对比Table 2 Comparison of anti-noise performance between two methods

在A相接地故障样本中添加20 dB噪声后，本文和文献［10］所提方法的重构误差、分类效果对比如附录A 图A8 所示。由图可见，本文和文献［10］所提方法均可正确分类，但是本文所提方法的重构误差指标eii接近于0，明显小于文献［10］所提方法的指标值，这表明本文所提方法的重构效果更好。文献［10］在噪声强度为16 dB 时出现分类错误的情况如附录A 图A9 所示。由图可见，根据式（13）所示的分类方法，文献［10］所提方法将该A 相接地故障样本错误分类为AB两相短路故障样本，产生了明显的重构误差，而本文所提方法可以进行正确分类。

3.4 泛化性能验证

为了验证本文所提方法的泛化性能，本文直接使用基于图2 的双端电源模型故障集的深度故障字典在附录A图A10所示的标准IEEE 9节点模型上进行验证。利用验证模型在3 个不同位置进行了各种不同故障条件的仿真，共计得到2520份故障仿真数据，基于本文所提方法和文献［10］所提方法的分类结果及重构误差均值对比如表3所示。

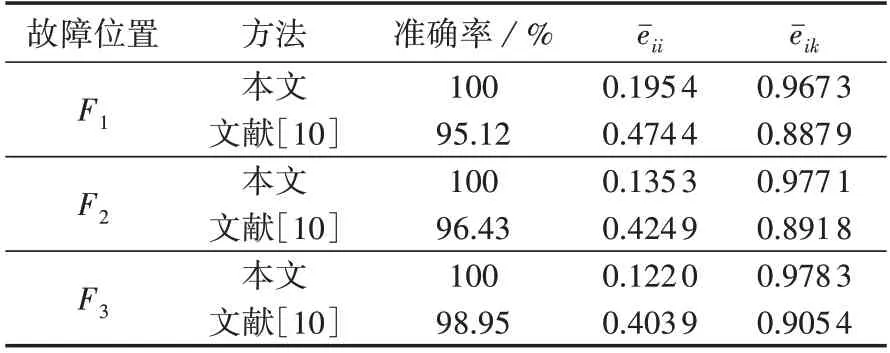
表3 2种方法的泛化性能对比Table 3 Comparison of generalization performance between two methods

从表3 可知，本文所提基于双端电源系统的深度故障字典模型在标准IEEE 9 节点模型的故障分类任务中取得了100%的正确率，高于文献［10］所提方法的正确率，表明本文所提深度字典模型的泛化性能要优于单层字典模型。

图4 为本文所提方法在eii最大时的样本分类效果。由图可见，即使在最坏的情况下，样本实际所属类别字典的重构误差与其他类别字典的重构误差之间仍有显著区别，本文所提方法仍可准确分类且分类结果具有较高的可靠性，将基于双端电源系统的深度故障字典直接用于其他输电系统中线路故障分类任务的可行性证明了所提算法的泛化性能以及将其应用于实际工程的潜力。

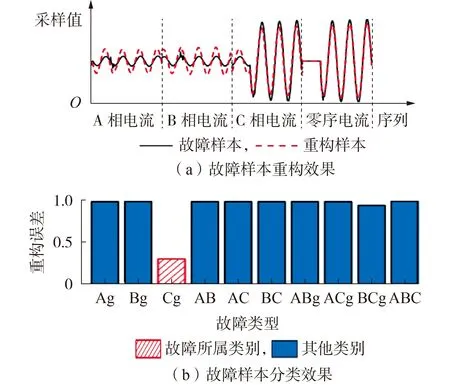
图4 标准IEEE 9节点故障集中，本文所提方法在eii最大时的样本分类效果Fig.4 Classification effect of sample with largest reconstruction error in standard IEEE 9-bus fault set under proposed method

3.5 故障特征的可解释性

如前文所述，深度学习等基于数据驱动的特征学习算法可解释性差，是本文想要解决的主要问题之一。即本文欲构建一个基于数据的特征学习模型，且所学习到的特征具有较好的物理含义。

高压输电线路故障后的暂态电流可表示为：

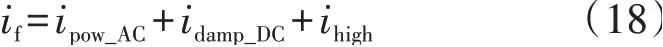
式中：if为故障后暂态电流；ipow_AC为工频电流分量；idamp_DC为衰减直流分量；ihigh为其他因素产生的高频分量。ipow_AC和idamp_DC可视为故障电流中的低频分量，ihigh为故障电流中的高频分量。

图5 为某故障样本及其基于深度故障字典的稀疏表示结果。图中：SF为故障样本；Lj（j=1，2，…，5）表示该故障样本在第j层对应的故障字典原子。由图5 可见，低层字典原子主要反映了故障样本的概貌特征，即式（18）中的低频分量，高层字典原子主要揭示了故障时刻的突变量等细节特征，即式（18）中的高频分量，且随着字典层数的增加，突变量等细节信息更为凸显。这种从由概貌到细节的层次化特征提取方式，符合人的认知过程，同时与实际输电线路故障信号的构成一致，具有较好的物理意义。

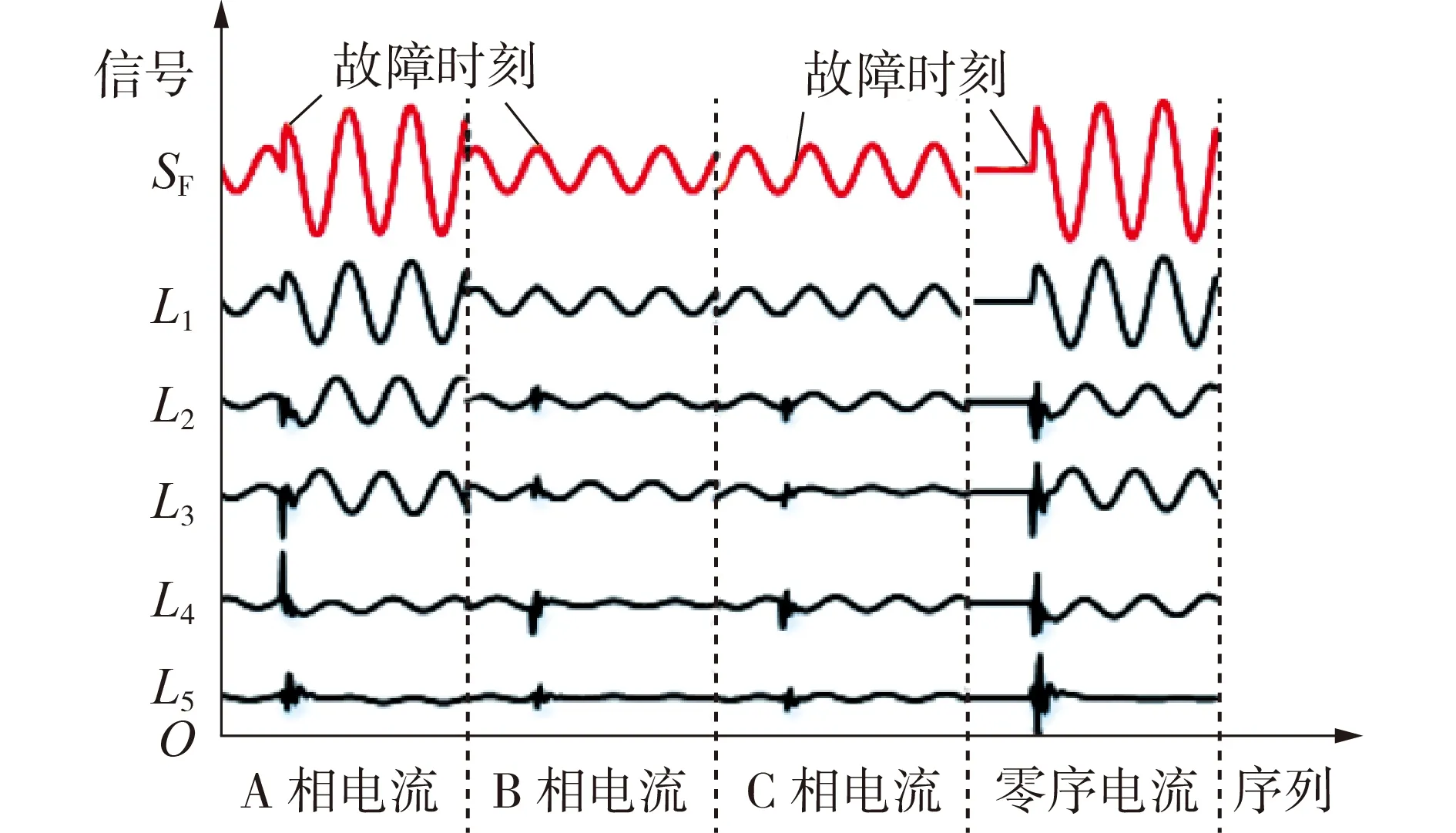
图5 待分类样本及其稀疏表示字典原子Fig.5 Sample to be classified and its dictionary atoms of sparse representation

进一步地，本文利用t-SNE 算法［23］对学习到的深度故障字典逐层进行降维可视化，结果如附录A图A11 所示。t-SNE 算法的基本思想是使高维空间相似的数据在低维空间（一般为2 维或3 维）的映射尽量接近，而差异较大的数据在低维空间的映射尽量远离。通过可视化降维后数据点在低维空间的分布，即可对原高维空间数据的相似程度有直观的感受。图A11所示的t-SNE可视化结果表明，各子层中同属一类的字典原子在降维后表现出明显的聚类特征，而不同类别原子映射到低维空间后距离较远。根据t-SNE 算法的特点可知，高维空间的同类故障字典原子是相似的，而不同故障类别的字典原子差异是显著的，这表明深度字典模型有效提取了不同故障类型之间的差异信息，且保持了同类故障特征的一致性。同时，结合式（18）和图5 可知，低层字典主要提取了故障电流中的低频故障特征，由于低频成分中包含一部分故障前的工频分量，这一分量是不受故障类型影响的，因此相当于低频故障特征中存在一定的“共模量”，具体表现为图A11 中低层字典的类间差异相对较小。随着字典层数增加，高层字典主要提取故障电流中的高频故障特征，避免了工频分量的影响，因此不同类间的故障特征差异更加显著，具体表现为图A11 中高层字典类间距离逐渐增大。上述可视化结果分析表明，深度故障字典有效提取了不同故障类型样本之间的从低频到高频部分的差异信息。