面向逆变器并联的虚拟振荡器控制技术综述

林燎源，柯 全，李 平

（华侨大学 信息科学与工程学院，福建 厦门 361021）

0 引言

为实现2030 年前碳排放达到峰值、2060 年前碳中和的国家战略目标，电力-能源-生态系统将发生重大变革，新能源发电技术迎来了全新的发展机遇［1］。由于新能源开发和利用的多样性，实现电能的转换对电力电子技术的要求越来越高。多逆变器并联控制是整合区域内多种能源资源、实现多能互补发电的关键支撑技术之一，能够极大提高供电系统的可靠性［2］。

目前逆变器并联控制已从非自治的主从控制、集中控制、分散逻辑控制等依赖信息交互的技术过渡至以下垂控制、虚拟同步发电机VSG（Virtual Synchronous Generator）控制和虚拟振荡器控制VOC（Virtual Oscillator Control）为代表的自治型并联控制技术，其显著特征是隐含自同步机制，因冗余度高、抗干扰能力强等优点而成为当前的研究热点［3-6］。下垂控制模拟了同步发电机并网运行的自下垂特性［7］，并基于等效阻抗特性进行扩展，根据有功、无功功率或其组合去调节参考电压频率和幅值，实现多逆变器自主并联运行。传统下垂控制中，在一定程度上下垂系数和所加虚拟阻抗越大，功率均分效果越好，但会造成输出电压和频率进一步偏离额定值［8］。与同步发电机相比，基于下垂控制的电力电子变换器缺少惯量支撑，使系统频率对负荷变化和扰动较敏感。而VSG 控制在下垂控制的基础上，模拟了传统同步发电机的惯量、阻尼和励磁特性，可改善逆变器的频率响应［9］。由于下垂控制和VSG 控制方案需采用低通滤波器计算输出平均功率，因此动态性能受到限制。

VOC 模拟了一类具有弱非线性的Liénard 振荡器的动力学特性，该振荡器一般可由二阶微分方程x¨+f(x)x˙+g(x)=0 描述，其中g(x)、f(x)分别为可微的奇、偶函数，在一定条件下Liénard 振荡器存在以恒定角频率旋转的唯一的稳定极限环，即在时域中生成正弦参考信号［9-11］。常见的Liénard 振荡器包括Dead-Zone型振荡器和Van der Pol型振荡器。Brian B. Johnson 团队先后将这2 种振荡器应用于逆变器并联运行控制［9，12-13］。由于不需要进行功率计算，因此VOC 相比下垂控制和VSG 控制可以实现更快的瞬态响应［3］。然而传统基于Van der Pol 型VOC 采用三次多项式的控制函数，可能引入较高的谐波含量（主要为3 次谐波）且缺少功率控制策略，这限制了该方法的并网应用［14-15］。文献［16］忽略控制函数中的3 次余弦分量，在保证同样同步速度的情况下能够输出较低谐波含量的电压波形。文献［17］通过引入一个与额定功率相关的复参数K实现了对输出功率的自由调度。观察Van der Pol型VOC结构，国外学者提出对增益系数ki、ku［18-20］或虚拟电容C［21-22］进行调节来控制输出功率。近年来，新提出的可调度虚拟振荡器控制dVOC（dispatchable VOC）［23-25］与安德诺夫·霍普夫虚拟振荡器控制AH-VOC（Andronov-Hopf VOC）［26-28］将功率设定点嵌入振荡器控制中，无需额外控制环路即可实现功率控制。与Dead-Zone 型和Van der Pol 型相比，新型VOC 可以生成无谐波的正弦电压参考且表现出更卓越的动态性能。尽管dVOC 与AH-VOC 提供了合适的构网控制思路，但它们的性能在电网发生故障期间容易受到限制。文献［29-30］提出一种统一型虚拟振荡器控制uVOC（unified VOC）方案，增强了故障穿越能力，扩宽了VOC 在未来电力系统中的应用前景。文献［31］针对并联逆变器并离网运行控制问题，离网采取Van der Pol型VOC，并网采取PQ 恒功率控制，同时使VOC 处于热备用状态，实现了2 种模式的平滑切换。

目前，国内外对VOC 技术的研究取得了一定的成果，主要面向不同工况下多逆变器同步运行、功率调度控制、系统小信号稳定性分析、与下垂控制／VSG 控制对比等问题。为便于描述，本文将基于Liénard 振荡器控制的VOC 简称为VOC，将基于该型VOC 的逆变器简称为VOC 逆变器。文献［32］已对不同类型振荡器的基本原理、参数设计以及存在的局限性进行阐述，本文在其基础上，进一步对面向逆变器并联运行的VOC 技术研究现状进行综述，从VOC 结构及改进方案入手，基于戴维南等效模型阐明多机运行的同步机理，归纳多种VOC 功率控制策略、小信号稳定性分析等方面的研究成果，在此基础上介绍近年来提出的几种新型VOC 实现方案及其特点，并总结VOC、下垂控制和VSG 控制的对比研究。最后，对VOC 技术面临的若干问题、未来研究方向和可能的相关解决思路进行探讨。

1 VOC结构分析

1.1 VOC逆变器结构

VOC 的控制思想受到“谐振变换器”的启发［33］，利用数字控制构造虚拟的LC振荡回路，将其谐振产生的正弦电压信号作为逆变器的电压参考，受控逆变器对外就能表现出该振荡器的物理特性［34］。单相VOC 逆变器的基本控制结构如图1 所示。图中：udc为逆变直流侧电源；Lf、Cf分别为滤波电感和滤波电容；Zline、Zload分别为线路阻抗和负载阻抗；ioso、uoso分别为虚拟振荡器输出电流和输出电压；io为逆变器输出电流；ki、ku分别为电流增益系数和电压增益系数；Ros、Cos、Los分别为虚拟电阻、虚拟电容和虚拟电感；isr为可控电流源-电阻双特性激励源模块SRM（Source-Resistance Module）输出电流。

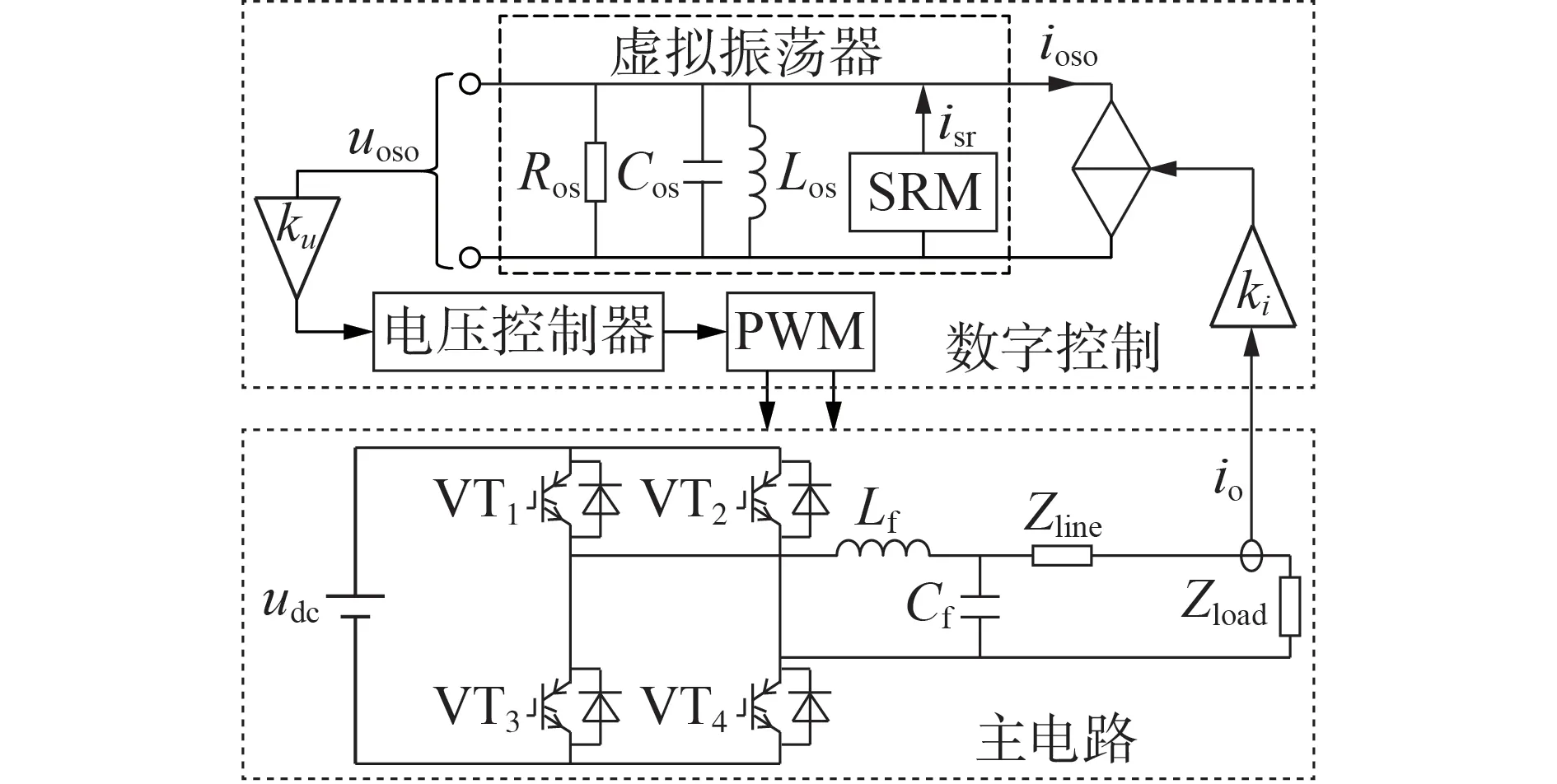
图1 单相VOC逆变器控制结构Fig.1 Control structure of single-phase VOC inverter

观察图1，虚拟振荡器由LC 振荡回路并联SRM与Ros组成，SRM 可工作于非线性电流源状态和非线性受控电阻状态，通过SRM 和Ros配合，可调节uoso的幅值［34］。uoso的频率由Cos和Los共同决定，设LC 振荡回路谐振角频率为逆变器输出额定角频率ω0，电容上的初始电压为UCm，电容存储的能量为W，则虚拟振荡器满足以下方程：

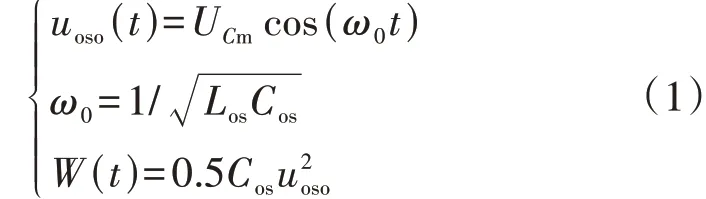
VOC逆变器主要包括逆变器主电路和数字控制系统。数字控制是核心部分，包含虚拟振荡器的振荡回路与控制算法，前者主要在机理上模拟LC谐振回路的电磁能量转换来生成正弦电压信号，后者主要用于控制振荡器的能量平衡与输出电压幅频稳定［35］。通过采样io，乘以ki用于控制ioso，与SRM 共同作用来调节uoso。uoso乘以ku，作为逆变器的正弦参考电压信号，经电压控制器得到脉宽调制PWM（Pulse Width Modulation）驱动的调制波信号，也可直接作为PWM驱动的调制波信号进行开环控制。

对于三相VOC 逆变器，当前主要有2 种思路。①移相变换法：采样三相逆变器某相输出电流反馈至振荡网络，对uoso分别移相120°与240°生成电压控制器的三相参考电压。②坐标变换法［36-37］：将三相输出电流变换至两相αβ坐标系下，取其中一相分量反馈至振荡网络，提取虚拟电感电流iLos，与uoso一起构成虚拟α β分量，再进行后续跟踪控制，如附录A图A1所示。可见，当前的振荡器形式仅考虑三相对称负载场合。

1.2 SRM控制函数设计

SRM 控制函数决定了uoso与isr之间的映射关系，其设计是虚拟振荡器中最重要的环节。同时振荡网络中还存在受控于逆变器输出电流的扰动电流源，使VOC 逆变器主电路、SRM 和振荡回路成为一个耦合体［35］，如附录A 图A2 所示。SRM 函数直接影响LC振荡回路的能量传递，进而影响VOC输出的参考电压质量。

对于给定的额定振幅Um，根据uoso的瞬时值大小，SRM 有电流源和电阻2 种运行模式。①电流源模式：当uoso的瞬时值小于Um时，为LC振荡回路提供能量，虚拟振荡器做自激振荡，其输出电压逐渐增大。②电阻模式：当uoso的瞬时值大于Um时，消耗LC振荡回路的能量，虚拟振荡器做减幅振荡，其输出电压逐渐减小。最终将输出电压uoso的幅值稳定在Um附近。

国外学者Brian B. Johnson率先对Dead-Zone型VOC 展开研究，提出如图2（a）所示的典型控制函数［34］，其表达式为：

为改善上述函数的控制偏差并缩短暂态过程，文献［35］提出了一种如图2（b）所示的改进函数，分别将uoso小于-Um和大于Um的部分函数下移和上移，在额定电压值处使SRM 发出能量等于Ros消耗的能量，振荡器达到等幅振荡状态。考虑到振荡网络中存在受控于逆变器输出电流的扰动电流源，文献［5］将图2（b）所示的函数模型进一步优化，提出一种考虑负载电流补偿的自适应VOC 方案，SRM 函数对应的函数曲线如图2（c）所示，一方面将自激振荡环节的函数斜率ksr进行非线性化，令ksr=kG（Um-uoso）+Gos（其中kG为比例系数，Gos为虚拟电阻的电导值），使其随输出电压uoso的改变而变化，函数的平滑处理不仅加快了自激振荡的起振速度，而且减少了输出电压在Um附近的波动，在稳态时有较低的波形畸变率；另一方面引入补偿电流kirio，通过动态调节电流补偿系数kir，使稳态时isr的增加量等于io，减小了io对振荡器的影响，在负载突变时能更好地保持端电压稳定。文献［38］进一步优化了负载电流补偿算法，通过计算VOC 电路的输出功率来决定SRM 对负载电流的补偿量，提高了系统的抗负载扰动性能。

由于分段函数形式不易于系统模型建立，现有文献大多采用如图2（d）所示的函数形式，即Van der Pol 型振荡器，输入输出呈三次多项式关系，其表达式为：

图2 Liénard振荡器的不同SRM函数形式Fig.2 Different SRM function forms of Liénard oscillator

式中：a为三次多项式三次项系数；b为形式2的一次项系数。Van der Pol 型振荡器为典型的谐波振荡器，其三次方运算使输出电压中的谐波以3 次谐波为主［9，39］，虽能通过参数设计选取一个近似圆形的稳定极限环以降低谐波含量，但会降低振荡器的动态响应性能，设计时需要进行权衡。可采用陷波滤波器滤除uoso的3 次谐波，但该方法会影响孤岛模式运行的逆变器并联系统的同步速度［16］。文献［16］对Van der Pol型振荡器SRM 控制函数展开研究，忽略函数中隐含的三倍频余弦量，降低了uoso的3 次谐波分量，并保持较快的系统同步速度。

由此可见，SRM控制函数的设计形式较为灵活，但总体而言，适应不同性质的负荷以及负荷变化工况，保持输出电压幅频稳定和更低谐波含量的SRM函数形式还有待进一步发掘。

2 VOC逆变器同步机制与动力学特性

2.1 VOC逆变器同步机制

逆变器的戴维南等效电路模型可表示为：

voi=Gci(s)vrefi-Zoi(s)ioi（4）

式中：vo为逆变器的输出电压；vref为逆变器的参考电压；Gc(s)为逆变器的空载电压增益，描述了输出电压跟踪给定参考电压的能力，其值一般约为1；Zo(s)为逆变器的等效输出阻抗，描述了输出电压应对负载扰动的性能；下标i表示第i台逆变器。

对于VOC 逆变器，将uoso作为逆变器参考电压，即vref=uoso。记逆变器的等效输出阻抗与馈线阻抗之和为Zt，结合虚拟振荡器结构和逆变器戴维南等效电路，以2 台VOC 逆变器（i=1，2）并联为例，可得其并联等效电路如图3所示。

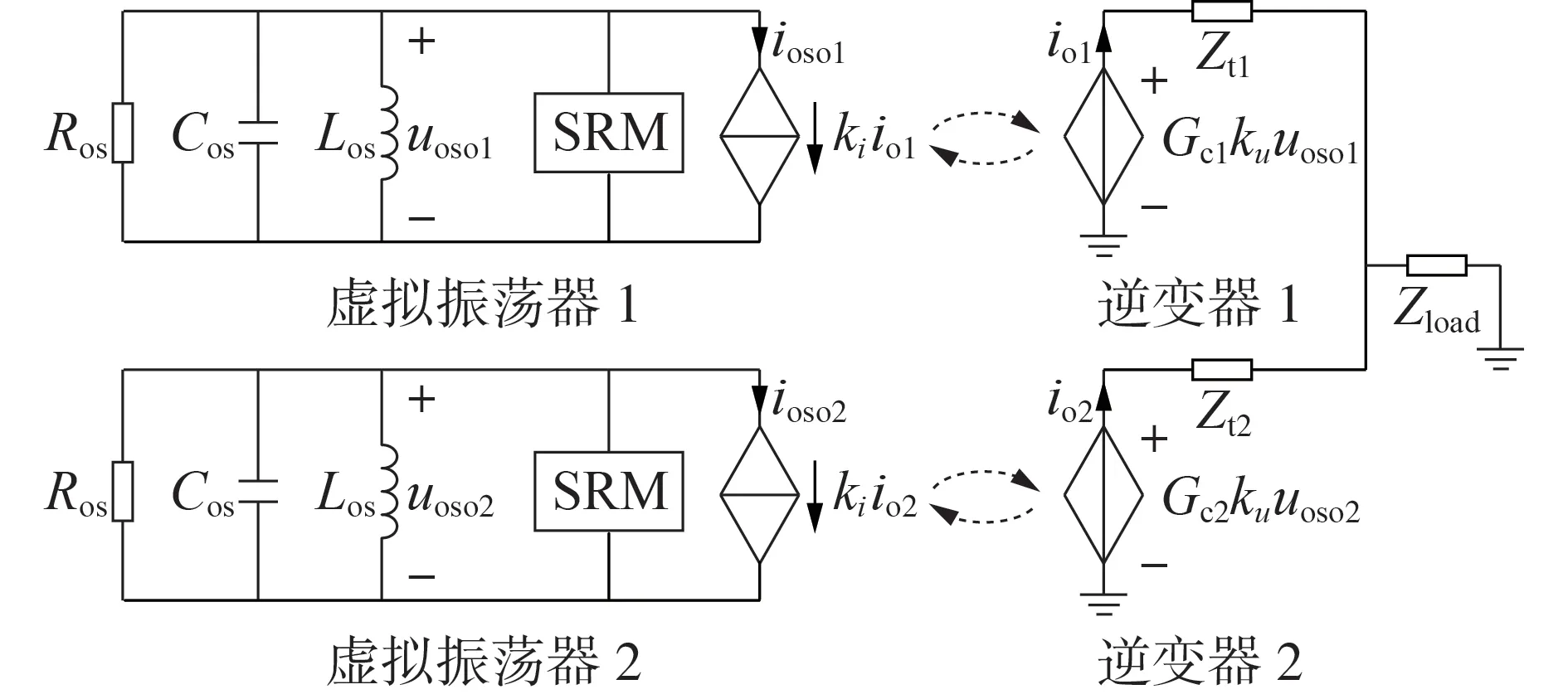
图3 2台VOC逆变器并联等效电路Fig.3 Parallel equivalent circuit of two VOC inverters

设ki与ku均为1，并代入Gc1≈Gc2≈1，可将图3进一步等效为图4 所示的虚拟振荡网络并联结构，即VOC逆变器并联可等效为虚拟LC振荡回路的并联。而LC振荡回路并联会发生耦合共振，最终形成一个稳定的新振荡体［38，40-41］。阻抗Zti一般很小，因此并联逆变器输出电压和电流将实现同步或近似同步。这是VOC 逆变器实现无互联线并联运行隐含的自同步机制，容易看出该同步机制与VOC 逆变器并联台数无关。VOC参数和逆变器参数的一致性能够实现多VOC 逆变器并联均流。需要指出的是，对于非同型逆变器组成的并联系统，由于逆变器电路参数、控制策略等不同会导致不同逆变器的空载电压增益与等效输出阻抗参数存在差异，进而影响并联系统的功率均分精度［42］。

图4 2个虚拟振荡网络并联示意图Fig.4 Schematic diagram of two virtual oscillation networks in parallel

基于上述耦合振荡器的自同步现象，VOC 除了应用于并联逆变器输出电压、电流的同步控制，还可以拓展应用到其他信号的同步调节中。文献［43］提出基于VOC 的并联逆变器载波同步控制，在无需通信的情况下实现了载波同步，从而抑制高频开关环流。类似地，交错并联Buck 变换器的PWM 载波信号也可以通过VOC 产生，具有模块化、可靠性高、成本低等优点［44-45］。需要指出的是，为保证反馈至虚拟振荡网络的正弦信号的完整性，一般要求VOC 对于该反馈信号的采样频率应远大于该反馈信号的频率，因此，VOC 应用于高频信号的同步控制时，对数字信号处理芯片的时钟频率及运算能力提出了较高要求。例如，文献［43］中开关频率为1 kHz，而采样频率高达200 kHz。

目前，VOC 逆变器并联的自同步条件分析主要基于李雅普诺夫稳定性分析方法。文献［46-49］推导了Dead-Zone 型VOC 逆变器的全局渐近同步条件为：

式中：sup 为表达式上界；ω为稳态时系统角频率；R表示实数集；Zosc为虚拟振荡器等效阻抗；‖ ‖· 为欧几里得范数。可知该同步条件与并联逆变器台数和负载参数无关，只取决于ki、ku、Zt和Zosc。对于VOC 逆变器，可通过振荡器参数设定和SRM 函数设计来实现同步运行［35，40］。

2.2 VOC的动力学特性

为探究VOC 的动力学特性，文献［9，19，50］采用工频周期平均法建立的基于Van der Pol 型振荡器的VOC的动力学模型为：

式中：θ为相对于ω建立的旋转参考系的相位偏移；φ为引入的一个可变角，通过φ的选择可得到对应不同阻抗类型的下垂方程的VOC 动力学模型；V、P、Q分别为逆变器输出电压、有功功率、无功功率；σ=1/Ros为虚拟电导；为参数x在一个工频交流周期内的平均值；xeq为参数x的稳态值。

式（8）、（9）揭示了稳态下VOC 平均动力学模型中隐含类似于下垂控制的下垂特性，其“下垂系数”受众多独立可调参数的复合控制。该模型为后续研究VOC 逆变器有功和无功功率自由调度、小信号建模、VOC与下垂控制对比研究提供了理论基础。

为验证基于Van der Pol 型振荡器VOC 逆变器隐含的下垂特性，参考文献［9］的参数设计过程，选取Los=5.208 7×10-5H，Cos=0.194 5 F，σ=10.796 2 S，ku=311，即振荡网络产生的参考电压额定值为311 V，额定频率为50 Hz。附录A 中表A1 与图A3 分别给出了单台VOC 逆变器中虚拟振荡器仿真测量结果和生成的参考电压波形。在t=2 s时，负载由30 Ω 电阻切换为15 Ω 电阻串联4 mH 电感，可以看到虚拟振荡器生成的参考电压的幅值和频率均发生了一定程度的偏移。

3 VOC逆变器功率控制策略

传统的VOC 结构中，在同步条件的约束下，VOC 参数一般设计为固定值，即逆变器输出电压不变。考虑到逆变器并联运行时应能按照额定功率容量承担负荷功率，文献［49］将ki与滤波器等效阻抗联系起来，指出模拟不同容量逆变器并联时输出功率按比例分配应满足：

式中：下标m、n分别表示第m、n台逆变器。但该结论考虑理想条件，且忽略了线路阻抗带来的影响，实际应用中无法实现对输出功率的精确调度。下面对目前已有的几种VOC 逆变器功率调度方法进行阐述。

3.1 电压、电流增益系数调节法

由VOC 的平均动力学模型可以看出逆变器输出电压幅值均受控于ki、ku，因此可以通过对功率偏差值进行比例积分（PI）运算来实时调节ku或ki，以实现有功或无功功率的精确调度［18，20，51-52］，基本思想如附录A 图A4 所示，图中Pref、Qref分别为有功、无功功率参考值。

由于有功、无功功率存在耦合，上述方法在设定的功率参考值发生变化时，可能导致输出有功、无功功率出现较大波动。同时，ki、ku的大小影响虚拟振荡器输出的参考电压幅值，即同时影响逆变器输出有功、无功功率，文献［20］建立了无功功率和有功功率控制环路中PI 控制器积分系数的正相关关系，缓解了无功功率变化时发生的有功功率过冲现象，但需要较长的动态调节时间。由于ki、ku与系统的同步条件相关，同步条件约束下PI 控制器的参数设计以及如何实现快速的动态响应还需要进一步研究。

3.2 引入复数增益系数K的功率控制法

文献［17］在负载电流增益系数之前引入一个复参数K，其模 ||K和相角ϑ分别由视在功率S的模和相角对参考值Sref的跟踪误差经PI 运算得到。通过设置积分器的增益系数与功率跟踪误差值的大小负相关，在功率参考变化时能够得到较为平顺的动态响应，控制框图如附录A 图A5所示。该文还提出一种有功、无功功率解耦控制方法，引入的2 个交叉耦合参数根据功率跟踪误差经2 个PI 控制器计算得到，仿真结果表现出一定的振荡抑制性能，但由于实际运行中线路阻抗参数的未知，引入的2 个交叉耦合参数仅是估计值，无法实现功率完全解耦。该方法一定程度上了提高系统输出有功、无功功率的跟随能力，且能实现有功、无功功率同时调度，适用于并网逆变器场合。

3.3 结合虚拟电容调节的功率控制法

由VOC 的平均动力学模型可以看出逆变器输出无功功率受到振荡器虚拟电容Cos的控制，因此，在通过对有功功率误差进行PI运算来调节ku以实现有功功率分配控制的同时，可以通过对无功功率跟踪误差进行PI运算来调节Cos，即分别调节VOC的输出电压与频率来实现有功、无功功率的分配控制［21-22］，基本思想如附录A 图A6 所示，图中ku0和C0为基准值。获取功率参考需借助通信网络，可以采取分层控制体系，文献［22］采用平均一致性算法，在二次控制层中逆变器与相邻单元交换功率信息作为功率参考。需要指出的是，当采用Cos作为控制变量时，由于该值受参考电压允许的幅频变化范围限制，因此调节逆变器输出无功功率的能力也相对受限。此外，通过添加电压和相位跟踪误差经PI 运算后的调节量至ku和Cos，可同时实现逆变器输出电压对电网电压或交流母线电压的同步跟踪控制［16］。

表1对比总结了VOC 逆变器实现功率精确调度的几种方案的优缺点，功率参考值的引入拓展了VOC 逆变器在并网运行中的应用，但参考功率的获取需要借助通信等手段，通信时延及故障的影响需要进行评估。此外，在负荷变化等工况下，外加的控制环路对虚拟振荡器输出电压的幅频特性以及自同步条件的影响仍需开展进一步的理论和实验研究。需要指出的是，当前文献侧重于并联系统中单台VOC 逆变器的控制性能研究，对于多台VOC 逆变器并联运行时系统的稳定性，如并联谐振及其抑制等问题，尚需进一步的研究工作。

表1 VOC逆变器功率控制策略总结Table 1 Summary of power controlstrategies of VOC inverter

4 小信号稳定性分析

控制器的非线性特征将增加系统建模的难度，现有的建模方案主要面向Van der Pol型振荡器，因其SRM 函数为非分段的三次多项式，可基于VOC 逆变器的平均动力学方程来建立逆变器单机或并联系统的小信号状态空间模型，利用特征值分析法进行小信号稳定性和参与因子影响分析。

Brian B. Johnson 等人用瞬时功率代替平均动力学方程中的平均功率，建立单机VOC 逆变器的小信号模型［53］，研究了滤波电感参数对系统稳定性的影响，发现在相同参数摄动下，VOC的主导极点相比下垂控制更加远离虚轴，因此具有更快的响应速度以及更大的系统阻尼，但该模型未考虑馈线阻抗及负载变化的影响。文献［54-55］则进一步将负载考虑在内，并通过二阶滤波器对瞬时功率进行滤波，分析不同参与因子对特征值分布的影响，并研究了负载扰动时系统的稳定性。

文献［56］建立了包含虚拟振荡器和逆变器主电路的多机小信号模型，利用主特征值分析法，研究了输出电压频率和幅值变化范围对系统稳定性的影响，指出允许的频率变化范围增大将加快VOC 的动态响应速度，但输出电压中的高次谐波含量会增加，导致波形畸变；而固定频率调节范围，端电压幅值调节对VOC的动态响应速度影响则较小。

文献［22］建立了包括VOC 逆变器、RL 负载、电力网络结构、二次控制器和通信时延的多母线孤岛微电网全局小信号状态空间模型，研究了二次控制器参数和控制时滞因素对系统稳定裕度的影响，指出较高的时滞会显著降低系统暂态性能，甚至使整个系统不稳定，在此基础上进行二次控制器的参数优化设计，并提出一种通信时滞补偿方案。

表2列出了现有文献基于VOC 逆变器的小信号模型对不同因素影响系统稳定性的分析结论。需要指出，目前提出的VOC 逆变器小信号建模是基于工频交流周期平均法，其时间窗口远大于传统基于开关周期平均的建模方法，该方法的适用性还需要进一步研究和论证。

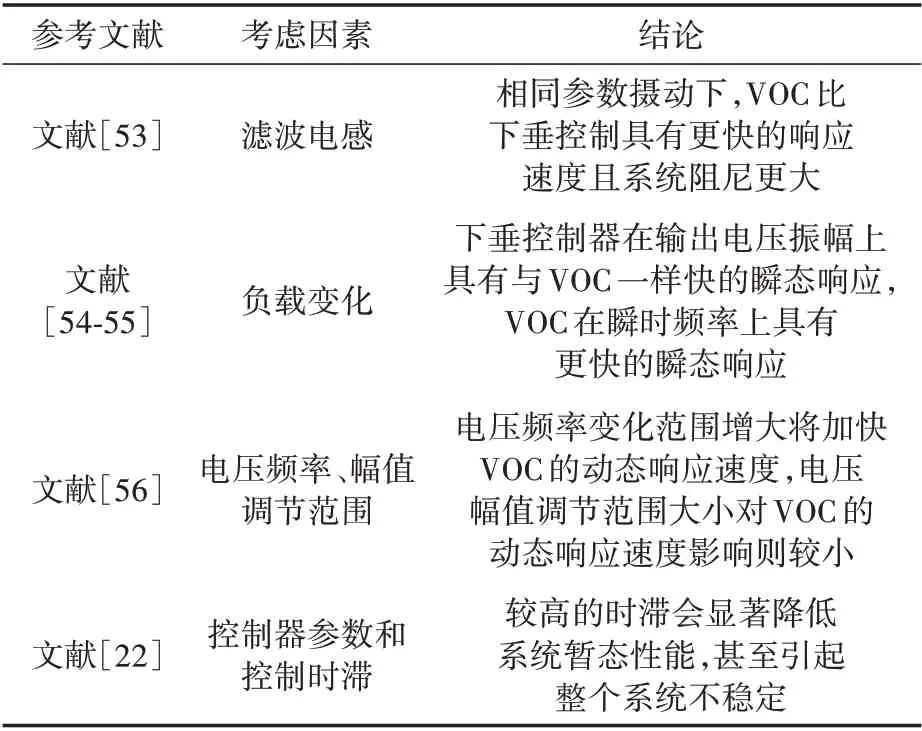
表2 小信号建模分析总结Table 2 Summary of small signal modeling and analysis

5 新型虚拟振荡器

前述基于Dead-Zone型和Van der Pol型振荡器的方案，虽在一定程度上改善了输出电压幅值和频率的波动以及功率分配问题，但仍存在以下不足：

1）根据Liénard 定理，非线性振荡器设计时需要保证存在稳定的极限环，极限环为圆形时才能得到理想的正弦波，而Liénard 振荡器无法得到理想的圆型极限环；

2）Dead-Zone 型和Van der Pol 型振荡器本身不具备有功、无功功率调度能力，需要添加额外的功率控制环路以跟踪功率参考。

针对以上问题，在Dead-Zone 型和Van der Pol型振荡器的基础上，延续发展出了以下几种新型虚拟振荡器控制方案。

1）dVOC。

dVOC 的基本思想是使电压额定值和同步反馈测量的电压幅值误差和相位误差最小化，并以额定角频率ω0在稳态下工作。通过在虚拟振荡器中引入瞬时功率的额定值和电压量，使VOC 具备了功率调度能力［23-25］。与传统VOC不同，dVOC的振荡频率和输出电压的额定值是直接给定的，一定程度上降低了参数设计的复杂度。在αβ坐标系中其控制方程可以描述为：

式（11）等号右侧第一项为dVOC 的基本部分，根据额定电压与额定频率生成参考电压；第二项为幅值校正环节，用于调节输出电压幅值与额定值匹配；第三、四项为相位校正环节，用于缩小额定电流与输出电流之间的相位差。

与传统VOC 类似，式（11）同样隐含了类下垂特性［23］。dVOC 的另一个优点是在稳态下能提供一个以恒定角频率旋转的极限圆，从而能生成理想的正弦参考电压［57］。但由于其控制方程与线路阻抗参数相关，目前的分析都是假设线路阻抗比为一固定值，然而实际工程中线路阻抗较难精确测定，线路参数变化时dVOC方案的鲁棒性需要进一步分析。

2）AH-VOC。

作为dVOC中的一种，AH-VOC在稳态下输出具有理想的极限圆，同样解决了传统VOC 中非线性振荡器带来的谐波问题［26-27］。文献［58］提出了Hopf分岔振荡器应用于逆变器控制的方案，指出其具有比Liénard 振荡器更好的负载均分性能和鲁棒性。AHVOC具有2个正交信号作为输入［59-61］，对比传统VOC方案，更适用于三相系统，其控制结构如附录A 图A7 所示。图中受控电压源vm和受控电流源im定义如下：

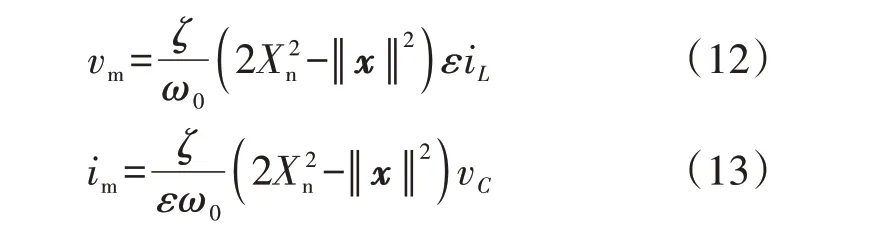
文献［62］通过分析指出AH-VOC 逆变器输出功率存在跟踪误差的原因在于其需要同时维持输出电压在额定值，通过求解潮流方程得到ku的设定值，考虑到系统阻抗参数难以精确测量，通过加入有功功率跟踪误差的积分运算值对其进行补偿，以实现稳态功率跟踪。文献［63］进一步将AH-VOC 拓展到逆变器并联系统中，考虑了由死区效应、非理想开关器件和滤波器引起的电压偏差，并引入电压、电流双环控制实现对输出电压的调节。

3）uVOC。

为使控制器具备在过载、短路等工况下的故障穿越能力，文献［29，64-65］在dVOC的理论基础上提出一种uVOC 方案，在并网模式和孤岛模式运行时具有统一的分析、设计和实现框架。通过在功率同步环路中嵌入限流器实现逆变器与任意幅值电网电压的同步，同时在故障穿越中具有快速的限流能力。然而该方案仅适用于电网发生对称故障情况。针对非对称故障，文献［30］提出一种双同步统一型虚拟振荡器控制dsUVOC（double synchronous UVOC）方案，采用2 个振荡器来实现对不平衡电网的正负序基频分量的同步，通过在同步环路中嵌入正负序矢量限流器，无需切换到备用的控制器或锁相环即可在对称或不对称故障条件下实现过流保护。

表3 给出了各振荡器的主要特征对比。从功率调度角度看，dVOC、AH-VOC、uVOC 因本身控制方程中带有功率参考值输入，因此能够实现功率自由调度。从谐波产生角度看，Dead-Zone 型和Van der Pol型振荡器的结构特征不可避免地带来谐波成分，合适的参数设计可以降低谐波含量，但会影响系统的动态性能。不同振荡器的参数设计可参阅文献［32］，本文不再赘述。一致的是，几种振荡器都隐含了下垂机制，因此有必要对比VOC、下垂控制和VSG控制的性能。

表3 不同振荡器比较Table 3 Comparison of different oscillators

6 VOC与下垂控制、VSG的对比研究

图5 给出了基于下垂控制［66］、VSG 控制［67］和VOC 的逆变器控制框图，可以看出，3 种控制方案都是输出正弦参考电压给后级的电压控制器，均为电压型控制。下垂控制、VSG 控制需要采样逆变器输出电压、电流进行平均功率计算，且一般需要低通滤波器平滑功率波动；而VOC 仅需采样输出电流瞬时值进行反馈，因此在快速响应能力上更具有潜力。

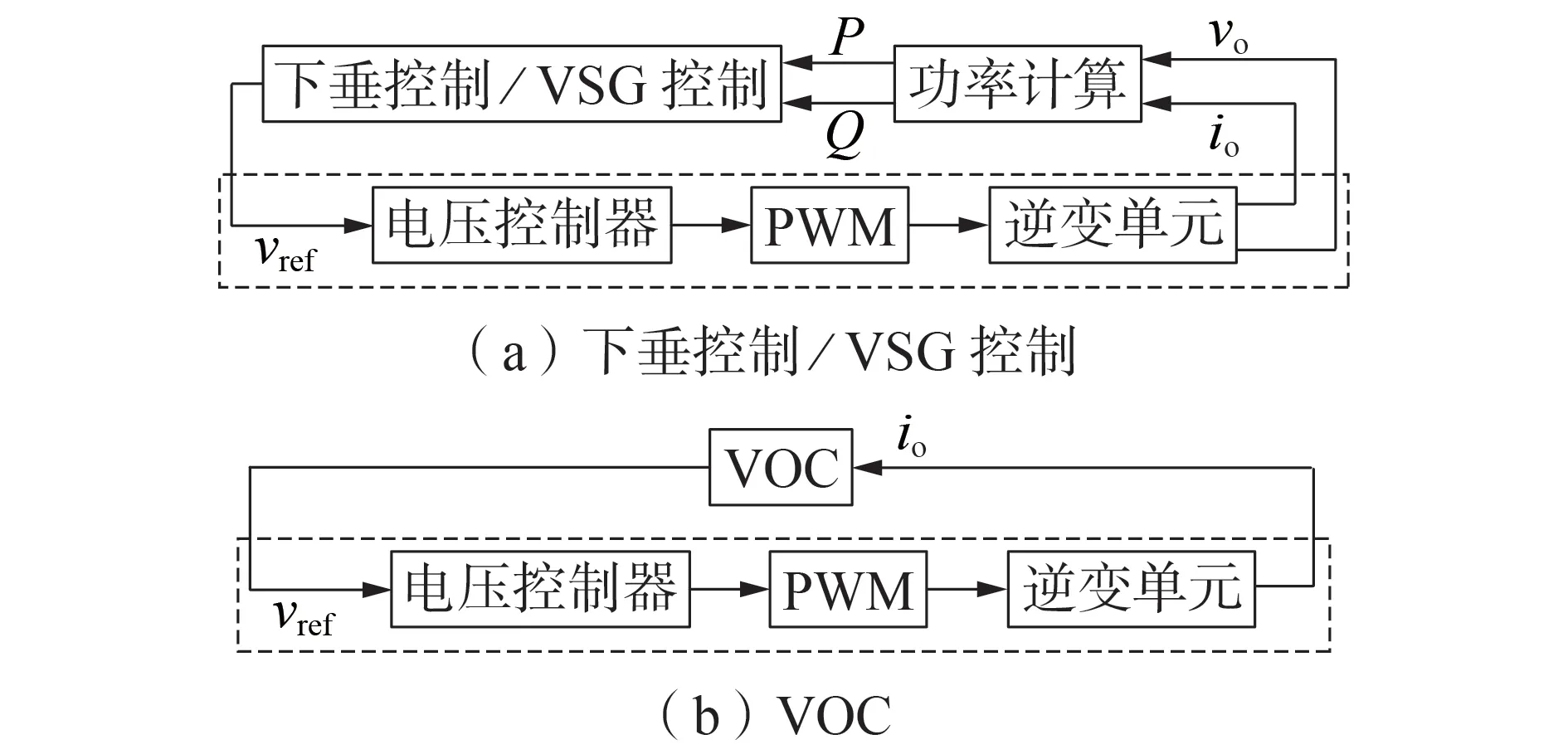
图5 逆变器控制框图Fig.5 Control block diagrams of inverter

如3.1节所述，VOC逆变器的平均动力学特性中隐含有下垂控制率，将下垂控制中的下垂系数按照一定的规则选取，VOC 与下垂控制可具有相似的稳态下垂特性［9，13］。文献［68］指出，下垂控制器的性能随着并联逆变器耦合程度的增加而变差甚至造成系统不稳定，而VOC 则随着耦合程度的增加而改善，下垂控制器更适用于高线路阻抗微电网，而在低阻抗微电网中，VOC是更好的选择。

文献［55］通过建立RL 负载下平均化后的VOC与下垂控制下单台三相逆变器的小信号状态空间模型，发现二者具有相似的主导极点，指出VOC 与下垂控制能够通过参数设计获得相类似的瞬态响应。文献［53］应用扰动法建立VOC 逆变器的小信号模型，通过系统特征根分析指出VOC 具有更优的动态性能和更小的暂态过冲。文献［56］通过多机小信号建模对系统特征根分布进行分析比较，指出带阻性负载、恒功率负载和非线性负载时，在允许电压频率变化较大时，VOC的暂态性能优于下垂控制，否则下垂控制更优。

文献［69］推导了对应于感性阻抗下的下垂方程的VOC 动力学方程，通过分析参与因子对特征根的影响，指出VOC 在瞬时频率响应速度上优于下垂控制，而在电压幅值响应速度上则表现较差。文献［3］在建立了VOC、下垂控制、VSG 控制小信号模型下，分析了滤波参数摄动下系统根轨迹的分布情况，发现VOC 特征值的负实部更加远离虚轴，意味着VOC具有更快的动态响应性能。实验结果还表明稳态下VOC逆变器输出电压具有更小的稳态误差。

文献［70］通过系统特征值分析法和仿真对比了AH-VOC 与传统下垂控制，结果表明AH-VOC 具有更优的动态性能。前述文献均从小信号分析角度进行比较，文献［59］则从大信号模型入手，采用圆上的向量场分析dVOC 的功角动态方程以评估其暂态稳定性，运用相图法分析下垂控制的暂态稳定性，结果表明在大的电网扰动下dVOC 具有优于下垂控制的暂态稳定性能。

表4 给出了VOC、下垂控制与VSG 控制部分特征的对比总结。在惯量支撑方面，在下垂特性的基础上，进一步模拟同步发电机的电磁特性及转子惯性，即为VSG 控制，可使逆变器具有惯性［71］。而VOC 逆变器之间的同步不依赖于惯性，初始功角为任意值时都能达到同步，因此不具有惯性的多VOC逆变器并联系统接入电网时，不会因电网整体惯性不足而出现不稳定，但在多种控制方式混合的多源系统（如VOC 逆变器、基于VSG 控制或下垂控制的逆变器、同步发电机组成的并联系统）中，若电网的整体惯性偏低会引起同步发电机的功角稳定性变差［72］。为增强VOC 逆变器系统的惯性，文献［72］在电流反馈回路上接入一个二阶广义积分器，利用其对输入信号的惯性延时作用，使VOC 逆变器具有与同步发电机类似的惯性，增强了多种控制方式混合的并联系统中同步发电机（传统电源）的功角稳定性。文献［32］提出一种将虚拟惯性合成到dVOC 的方法，将dVOC的功率设定值PVI改写为：

表4 VOC、下垂控制和VSG控制对比Table 4 Comparison of VOC，droopcontrol and VSG control

式中：Δω=ω-ω0；KI为惯性系数；KD为阻尼惯量。此外，文献［73］通过向AH-VOC 接入比例微分控制器，为系统添加了惯量支撑，在低惯量系统中为发电功率和需求功率的不平衡造成的频率偏差提供补偿。

综上可知：在动态响应上，由于VOC 作为一种时域控制器，利用逆变器瞬时输出电流作为反馈量，无需计算平均功率，因此在响应速度上具有优势；稳态时，在合理设计VOC 参数的情况下，其生成的参考电压对比下垂控制与VSG 控制具有更小的幅频偏差［3］；在惯性支撑方面，已有前述方案能够赋予VOC 逆变器类似与同步发电机的惯性，但这些方案的暂态、稳态特性以及与VSG 控制的对比尚未深入研究。

7 进一步研究展望

VOC 作为一种新型的多逆变器并联控制技术，在控制性能上表现出优异的潜力，已有研究在振荡器结构、功率控制策略和小信号稳定性分析方面取得了一定成果。然而，由于VOC 的非线性特性及其与逆变器主电路基于输出电流反馈的耦合交互机制，其在幅频控制、非线性负载、三相不平衡负载、非同型逆变器并联等应用场合中实现精确功率调度和输出电能质量优化等目标尚需进一步研究。

1）虚拟振荡器输出电压的幅频控制问题。

虚拟振荡器的振荡控制是一种瞬时值控制方式，由于LC 振荡回路的储能具有“惯性”，若未在L或C 元件能量为0 时改变SRM 工作模式，则难以避免uoso幅值存在超调，造成幅值控制偏差。此外，VOC 基于“LC 谐振”的频率输出机制，使逆变器在带感性或容性负载时，由虚拟电感、电容决定的额定频率会受到负载的影响而引起频率偏移。从VOC 隐含的下垂特性也可知其输出电压的幅频特性受到负载影响。考虑到VOC 幅频调节的隐性特征，可考虑引入分层控制，通过在二次控制层中对电压增益系数、虚拟电感和电容值等参数进行调节，补偿幅值与频率偏差，将输出电压恢复至额定值。

2）电流谐波对振荡网络的扰动问题。

虚拟振荡网络中存在受控于逆变器输出电流的扰动电流源，带非线性负载或并网运行时若输出电流存在谐波分量，该分量将进入虚拟振荡器网络，直接对振荡器输出电压造成污染，从而影响逆变器输出电压的电能质量。目前，VOC 逆变器并网运行中常采用陷波滤波器来抑制振荡器输出电压谐波含量造成的谐波电流，但无法抑制来自电网侧的谐波［74］。文献［75］采用虚拟阻抗调节VOC 逆变器在谐波频率处的等效阻抗，来抑制并网电流谐波，然而虚拟阻抗的引入降低了逆变器输出电压幅值，且对于多个谐波频率下的高增益谐振可能会对整个系统的稳定性造成影响。文献［76-77］采用卡尔曼滤波器估计在公共耦合点处的电压谐波含量，并将其嵌入VOC逆变器的前馈控制回路中，与虚拟阻抗法相比对并网谐波电流的抑制效果更强。

振荡器输出电压存在谐波的根源在于振荡器本身的动力学特性以及反馈至振荡网络的逆变器输出电流谐波分量。前者可通过调整振荡器控制参数来缓解或采用前述新型VOC 方案；后者可对电流提取基波分量再进行反馈。但VOC 逆变器的动态性能和谐波抑制能力是一个权衡问题，较好的动态性能会带来更大的谐波失真［9，68］。

3）三相不平衡负载下的VOC方案。

目前基于VOC 的三相逆变系统研究主要针对三相对称负载的情况，通过对三相输出电流进行αβ变换作为振荡网络的电流反馈量，并输出三相对称电压参考信号。显然，当前的VOC 结构本身并不具备三相不平衡抑制能力，因此可由后级的电压控制器来承担该功能需求，目前针对三相电压不平衡问题的补偿方法主要是基于正负序分量分解反馈技术［43，78-79］。此外，模型预测控制、滑模控制等非线性控制器可以在一定程度上克服传统线性控制在不平衡电压补偿方面的不足，可考虑作为VOC 的后级电压控制器。另一方面，可从VOC 本身入手，可尝试对目前的振荡器结构进行拓展，如构造三相结构的虚拟振荡器等，在应对三相电压不平衡问题上有潜在优势。

4）VOC应用于非同型逆变器并联系统。

在微电网、以智能电网为主体的综合能源系统等电力电子化的多能源发电系统中，不同厂商生产的逆变器装置共存将逐渐常态化，意味着非同型逆变器需要具备直接并联运行的能力。而目前基于下垂控制、VSG 控制和VOC 的逆变器并联大多以同型逆变器作为理论、仿真和实验研究的对象，即考虑协同运行的逆变器具有相同的拓扑、电压控制策略和参数，主要考虑逆变器外部特性特别是阻抗（逆变器等效阻抗及连线阻抗）特性失配带来的问题。非同型逆变器的不同内部特性对输出电压的动静态响应会表现出不同的动力学特性，进而影响并联系统的性能。基本地，如前述，逆变器电路参数、控制策略等不同会导致不同逆变器的空载电压增益与等效输出阻抗参数存在差异。因此，针对非同型逆变器的VOC等自治型并联控制技术的进一步深入研究亟待进行，可从电压跟踪控制器入手，探讨能够严格跟随参考电压的控制方法，从而消除数学模型上不同逆变器之间的特性差异。

8 结语

电力电子技术驱动下的分布式电源广泛接入逐渐在能源结构优化中起显著作用，VOC 技术的提出为逆变器无互联线并联运行提供了新的控制思路，丰富了多逆变器并联系统的运行控制方法，具有良好的应用前景。本文在总结大量国内外VOC 相关文献的基础上，从VOC 控制结构、并联运行同步机制、动力学特性、功率控制、小信号稳定性分析、新型VOC 方案等方面进行了全面综述，阐述并总结了当前VOC 与下垂控制、VSG 控制的对比研究结果，结合VOC 的特点及应用场合探讨了VOC 技术尚面临的若干关键问题及相关解决思路。希望本文能为VOC技术的进一步研究和发展提供有益参考。

附录见本刊网络版（http：//www.epae.cn）。