考虑新能源不确定性的互联电网交换功率鲁棒优化模型

2022-11-19樊小伟孙荣富王靖然孙宏文董晓明

电力自动化设备 2022年11期

樊小伟，孙荣富，王靖然，马悦，孙宏文，陈全，董晓明

（1. 国网冀北电力有限公司，北京 100054；2. 山东大学电气工程学院，山东济南 250061）

0 引言

多区域互联电力系统能够促进风电、光伏等可再生能源在全网范围内实现优化配置和合理消纳。然而，新能源出力的不确定性将导致区域间联络线传输功率发生较大波动，并且各区域之间电网运行状态信息交互不完全、不及时，在一定程度上会形成“信息壁垒”，这给交流互联电力系统的调度运行带来了巨大挑战［1-3］。随着互联电网的规模不断扩大，具有随机特性的新能源大规模跨区域流转和各分区电网调度运行相对独立的矛盾日益突出，区域间联络线功率波动的调控问题亟需妥善解决。当交换功率波动过大时，相邻区域电网运行态势会产生较大波动，进而导致送、受端电网承担的交换功率过大，潮流难以疏散，最终可能引发安全稳定问题。特别地，当多条联络线功率分配不均衡，且重载联络线功率波动幅值过大超越限值，甚至被迫停运时，联络线间的潮流转移可能引发连锁性故障，导致大停电的发生［4-6］。因此，减小和抑制区域之间联络线的功率波动具有重要意义。

为了抑制新能源系统并网引发的联络线功率波动，国内外学者进行了大量相关研究。文献［7］建立了基于两阶段随机规划的微电网市场互动优化模型，在以经济性和不影响用户用能为原则的情况下实现了联络线功率波动平抑；文献［8］将不确定性的空间约束参数引入传统鲁棒优化模型，并采用基于滤子技术的协同进化算法对该模型进行求解，以达到抑制联络线功率波动的作用。文献［9］提出直流功率调制抑制交流联络线随机功率波动的方法，通过直流功率调制快速吸收或补偿其所连交流系统的过剩或缺额功率来减少交流联络线上的随机功率波动。文献［10］提出基于非线性PI 控制的特高压联络线功率波动抑制策略。文献［11］提出基于“改进的独立稳集”的双级直流微电网群稳电控制策略，算例结果验证了其降低联络线功率波动的有效性。文献［12］提出基于双层模型预测结构的跨区域自动发电控制AGC（Automatic Generation Control）机组协同控制策略，实现了多区域间共享调频资源。文献［13］在考虑联络线支援约束的情况下，提出一种新的基于区域调节边际成本的多区域AGC 最优联合调频控制策略。文献［14］基于市场均衡机制提出一种用于平抑微电网联络线功率波动的空调负荷协调控制方法。文献［15］提出一种蓄电池和虚拟储能的协调控制策略，用于有效平抑微电网联络线功率波动。上述研究主要目标为考虑区域互联的经济性指标最大化，而关于区域间联络线的功率波动平抑的研究还处于探索阶段，研究成果较少。文献［16］提出一种多区域潮流外特性稳定控制模型，但其未考虑区域联络线上支路阻抗的影响，这将会导致区域间参考相角随着功率转移而产生偏移。

随着电网规模不断扩大，区域联络更加紧密，对AGC的控制策略也提出了更高的要求［17-19］。新能源在大范围流转实现资源互济，互联系统各个分区的AGC［20-22］在保障区域内功率平衡的同时，要求较好地平抑断面交换功率波动，且各联络线功率均衡分布，确保互联系统安全稳定运行。据此，本文将AGC 引入潮流方程，构建了考虑AGC 功率分配的互联系统潮流模型。以此为基础，建立了以平抑联络线功率波动为目标函数的鲁棒优化模型，并提出了基于松弛法的协同演化求解算法。最后，基于双IEEE 14 节点以及IEEE 118 节点测试系统构造仿真算例，验证了所提方法的有效性与实用性。

1 AGC下的互联系统潮流模型

1.1 区域内潮流平衡

AGC是电网调度自动化系统的核心并对电网安全运行起着至关重要的作用。多区域电力网络中各子区域具有独立的AGC 系统。各分区AGC 系统除了维持子区域内部的有功潮流平衡，同时还调控区域间的有功功率的交换。可将AGC 的调控作用视为系统中的多台平衡机按比例（分配因子）协同作用，分担不平衡功率。假设各子区域与外部区域有功交换为固定值，如式（1）所示。

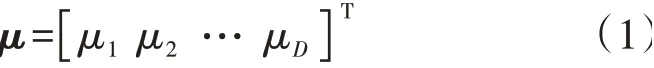
式中：D为子区域总数目；μj（j=1，2，…，D）为第j个子区域从其他子区域获取的有功功率总和，受电时其值为正，送电时其值为负。将多区域电网中所有母线数用n表示，可以得到如式（2）所示的参与因子矩阵α。

式中：αij（i=1，2，…，n；d=1，2，…，D）对应矩阵的第i（母线节点编号）行、第d（子区域编号）列的元素，为第d个子区域第i条母线在AGC 中的参与因子。如果第i条母线不在第d个子区域中，则αid=0；如果第i条母线在第d个子区域中，但是不参与AGC 调节，则αid=0；如果第i条母线在第d个子区域中且参与AGC 调节，则αid≠0。矩阵每一列元素，即每个区域内的AGC分配因子满足式（3）所示的关系。

式中：i=1，2，…，m，其中m为多区域网络中所有PQ节点数；j=1，2，…，n；V和θ分别为由所有节点的电压幅值和相角组成的向量；Pj和Qi分别为注入节点j的有功功率和注入节点i的无功功率；fi表示节点i

式中：j∈i表示节点j与节点i相连；Gij和Bij分别为节点i和节点j之间的互电导和互电纳；θij=θi-θj为节点i和节点j之间的电压相角差，θi、θj分别为节点i和节点j的电压相角。

1.2 区域间断面潮流控制

在某一时刻，区域间断面的交换功率按照一定的计划值进行调控，是互联电网能够安全可靠运行的重要边界条件，要求电网正常运行状态下各断面潮流不越限。对于多区域互联电网，区域间的潮流断面控制通过AGC 完成，形成的断面潮流方程如式（7）所示。

式中：Φd为第d个子区域内的边界联络线集合；Ωd为第d个子区域内的边界节点集合。

将式（5）和式（7）联立，可得AGC 下的多区域潮流统一模型如式（11）所示。

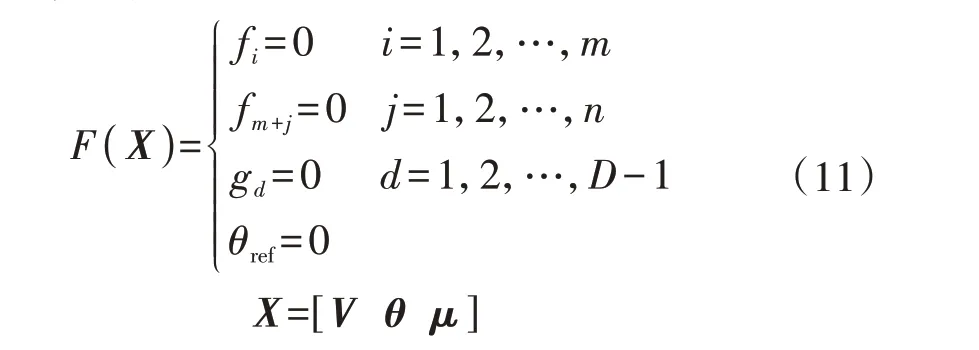
式中：θref为预先设定的参考母线相角。

2 区域潮流外特性稳定控制模型

2.1 区域潮流外特性分析

在多区域互联系统中，区域内和区域间的有功功率平衡都由各个子区域内AGC 完成，区域间的功率传输通过区域联络线实现，而联络线传输的有功功率大小与联络线两端的相角及其差值密切相关。即各区域的边界节点之间的相角差，会随着多区域AGC 的协调控制发生变化，以维持区域间功率交换的稳定。当某个子区域的相角变化很大时，与其相连的外部区域边界节点的相角必然需做出相应调整。两区域互联网络潮流变化如图1 所示，每个子区域有3个边界节点，通过边界节点2个子区域产生功率交换。每个子区域内都指定一个参考节点的电压相角，随着AGC 的控制调整，参考节点电压相角相应改变，使得联络线上流过的功率之和P1+P2+P3保持在设定值（μ）不变。

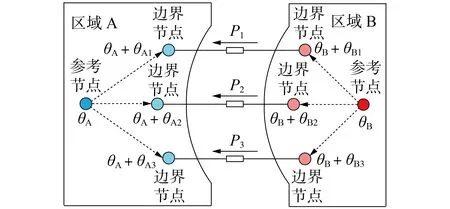
图1 两区域互联网络潮流变化Fig.1 Variation of power flow in interconnected network between two areas

区域A 与区域B 之间的传输功率可线性化表示为：

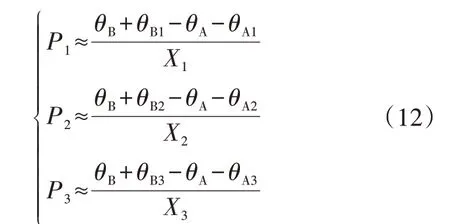
式中：X1、X2、X3和P1、P2、P3分别为边界联络线A1-B1、A2-B2、A3-B3上的电抗值和流经的有功功率；θA、θB分别为区域A 和区域B 内的参考节点相角；θA1、θA2、θA3和θB1、θB2、θB3分别为区域A 和区域B 边界节点与区域内参考节点的相角差。

由式（12）可以看出，区域联络线上的潮流波动主要受子区域内边界节点的相角变化影响。当区域B 内的相角波动时，也将使得区域A 相角发生变化。在多区域计算时，考虑到分区间信息保密或信息传递滞后的情况，对于某一子区域（以区域A 为例）而言，无法获取到区域外（区域B）边界节点的功角变化信息。据此本文首先忽略区域外节点功角变化，在子区域内独立计算时将其设为常量，并结合边界相角调整策略，逐步缩小误差，实现多区域潮流渐近的匹配。

为此，本文计算过程中区域A 的电气参量为未知量，令ΔθA1=0，其中Δ 表示相应变量的变化量。此时联络线上功率变化值的计算公式如（13）所示。

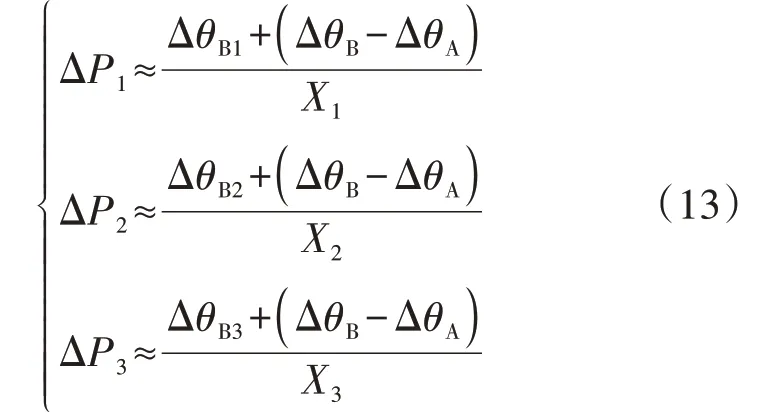
2.2 基于鲁棒优化的多区域稳定控制模型

对于多区域互联电网的某一子区域，发电运行方式的部署及优化调整往往仅局限于子区域内部。以中国为例，各省网在考虑边界联络线的输送功率的基础上，独立规划省内发电运行方式并形成“年-季-月-周-日”的运行计划。同时，各省网内部的调度及运行状态信息，在分区间进行传递时，也存在信息交互不及时、不完全的情况，各个分区调度运行的自治和全局实时统筹协调之间仍然存在矛盾。因此，区域内发电按计划执行的同时，维持区域间联络线潮流流动的稳定，尽可能减少子区域功率随机波动对外部电网的影响，是必要且有效的控制方法。鲁棒优化作为可以处理不确定性参数的优化方法，被广泛运用在电力系统中以解决不确定参数的优化问题。本节将建立多区域潮流稳定控制鲁棒模型。

2.2.1 目标函数

计及新能源出力的不确定性，目标函数设置为联络线上功率变化幅值最小，其表达式如式（14）所示。

式中：ΔP t为所研究子区域与其他子区域的联络线上流动的有功功率变化量；Pr为所研究子区域内可能发生变化的新能源发电出力。

研究某一子区域时，假定该区域以外其他区域不发生功率扰动，令式（13）中ΔθA=0。在此假定下将联络线有功功率按式（13）线性化后可得：

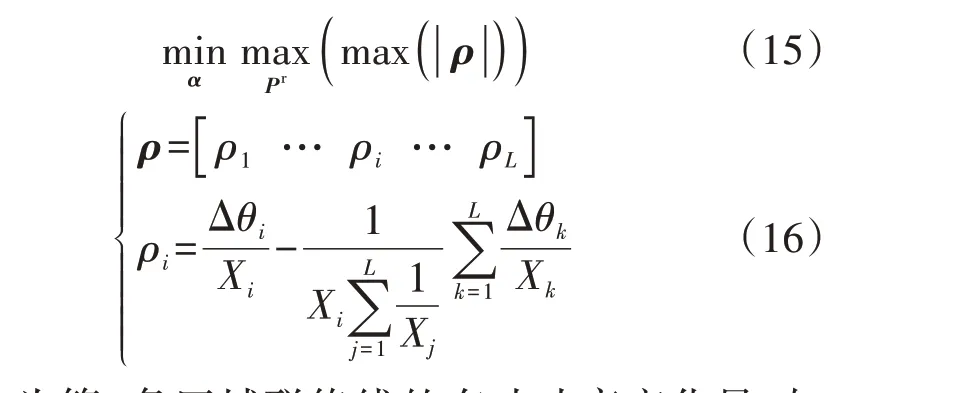
式中：ρi为第i条区域联络线的有功功率变化量，如果第i条区域联络线与所研究子区域相连，则按照式（16）计算，否则取0；Δθi为第i条区域联络线与待研究子区域内相连节点的相角变化量。

2.2.2 约束条件

鲁棒优化模型的求解需满足以下约束。1）功率平衡约束。

基于式（5）可以将功率平衡约束描述为Fs，如式（17）所示。

5）新能源出力短时变化范围约束。

基于数据统计可以得到单位时间内新能源出力增大或减小的变化范围估计值，如式（21）所示。

式中：f和分别为网络支路的有功潮流及其上限。向量f中的元素fij具体表达式如式（23）所示，fij为节点i和节点j之间传输的有功功率。

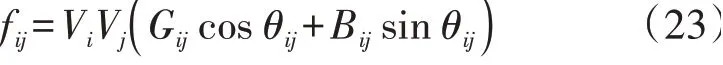
2.3 模型线性化处理

由于原问题属于鲁棒优化问题，且约束中带有非线性等式，求解难度大，为此本文对模型中的功率平衡约束和线路功率约束进行线性化处理，以提高求解速度。

1）在功率平衡约束中，式（17）为非线性方程组，线性化处理后如式（24）所示。

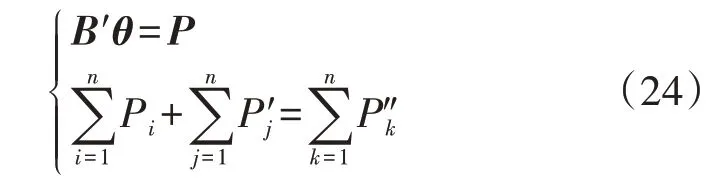
式中：P″k为节点k处负荷的有功功率；θ和P为n维列向量，分别由n个节点的相角和节点注入有功功率构成；B′为n×n维矩阵，其中各元素可依据式（25）计算得到。

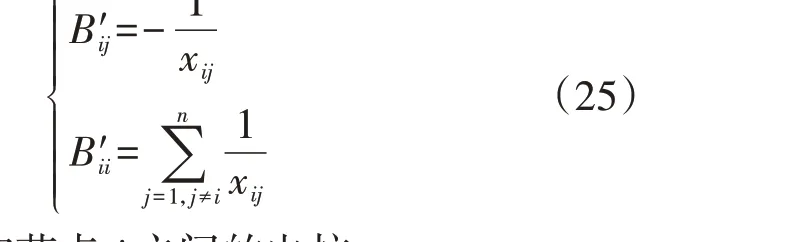
式中：xij为节点i和节点j之间的电抗。

2）对于功率约束中不等式的非线性主要体现在式（23），可以线性化为式（26）。

3 基于松弛的演化求解方法

普通优化问题仅针对单一的优化目标，而鲁棒优化问题的解是一个零和博弈的纳什均衡解，在寻找令优化目标最优的决策量的同时，也需要搜索令优化目标最差的环境变量，常规优化算法难以满足这一要求。目前广泛采用的方法是基于对偶原理将鲁棒优化问题转化为普通优化问题，但是本文建立的非线性约束是同时包含环境变量和决策变量的问题，对偶原理难以适用。因此，对于如式（15）所示的目标函数，将其转化为如式（27）所示的通用数学表达式。

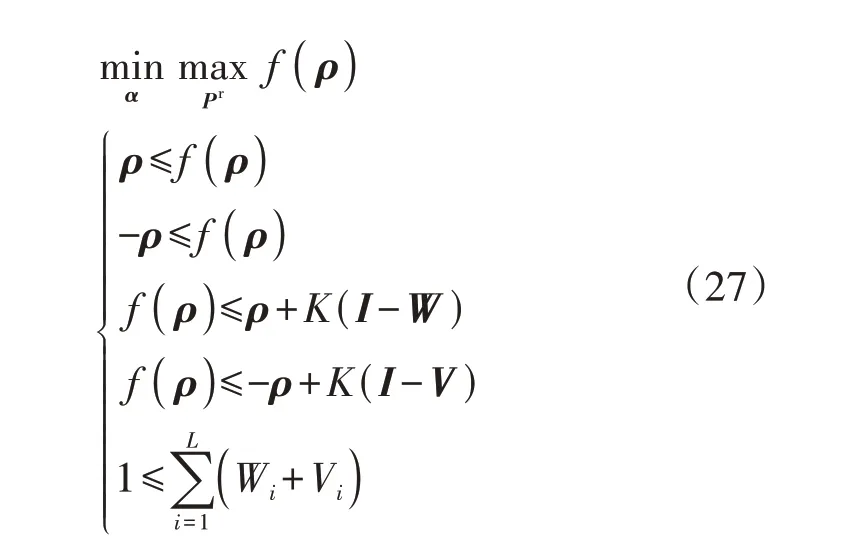
式中：W和V为由0-1 变量组成的1×L维向量，即W=［W1…Wi…WL］，V=［V1…Vi…VL］；K设置为一个绝对值较大的正数；I为1×L维的单位向量。

由于ρ由矩阵α和Pr决定，因此多区域潮流稳定控制模型的目标函数可转化为式（28）。

由于x和y的取值存在无限可能性，式（30）中包含了无限个约束条件，因此常用的分支定界法难以适用且求解困难，为此，使用松弛法将式（30）转换成如下松弛化问题：

4）若fA-fa＜ϵR（ϵR为求解精度），则计算结束，返回(x*，y*)，否则将y*添加至SY中，返回步骤2）。

4 算例分析

4.1 算例系统描述

为对比鲁棒优化模型与无优化模型在区域外特性不同时计算结果的差异性，本文采用2 个IEEE 14 节点系统并联，形成算例系统。2 个系统通过2 条联络线相连，一条联络线连接区域1 的节点4和区域2 的节点24，另一条联络线连接区域1 的节点13 和区域2 的节点213。区域1 将节点5 作为参考节点，相角设为0°。区域1 的节点3 和节点8 处接入风电机组，节点1、节点2、节点6 接入采用AGC 的常规火电机组（下文简称常规机组）。相应地，区域2 均接入采用AGC 的常规机组。双IEEE 14 节点测试系统示意图具体如附录A图A1所示。

设定子区域1 向子区域2 输送100 MW 功率。算例结果与分析均以子区域1 为参考。设定2 台风电机组出力波动范围均在0～100 MW 间，电网内风电允许的最大波动偏差可根据以往的历史预测偏差进行设定。本文中考虑风电出力的波动偏差分别为预测值的10%［21］。在AGC 下的常规机组出力范围在0～500 MW 间，节点1、节点2、节点6 处常规机组出力初始值分别设定为100、100、200 MW。本文在MATLAB 环境中通过YALMIP工具箱调用CPLEX 求解器对所提模型进行求解。

4.2 算例结果分析

式（2）所示的参与因子矩阵可以认为是对应系统中AGC 在本区域内对不平衡功率进行调整贡献度，也是影响电网内常规机组出力的重要因素。由于参与因子矩阵是一个稀疏矩阵，除少数非零元素之外均为0，因此图2仅展示了依据本文算法得到的24 h 下3 台常规机组所在母线的AGC 参与因子计算结果，分别对应参与因子矩阵中的α11、α21、α61。

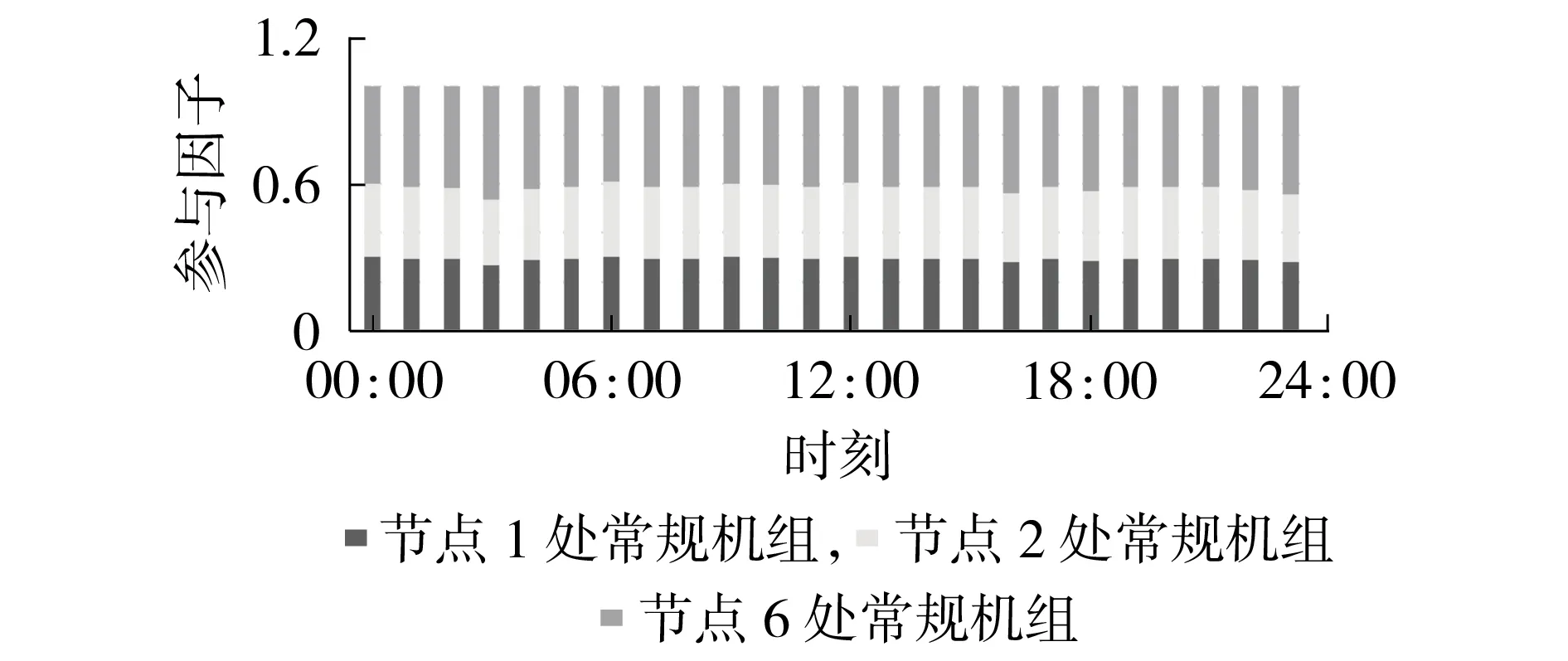
图2 AGC参与因子变化情况Fig.2 Variation situation of participation factor for AGC

观察图2 可得，节点1 和节点2 处的常规机组在不同时刻的AGC参与因子在0.3上下浮动，节点6处的常规机组在不同时刻的AGC 参与因子在0.4 上下浮动。由附录A图A1可得节点6处的常规机组距离重负荷区域较近，因此其承担相对较多的不平衡功率。

由于采用鲁棒优化时的计算结果不同于无优化时的计算结果，为了方便表示2 种方法计算对外特性的差异，并能较好展示，用式（32）表示。

δ=gt+1-gt t=1，2，…，23 （32）

式中：gt+1-gt为相邻两时段计算结果的差值。令δ1表示无优化时相邻时段的相角或功率波动，δ2表示采用鲁棒优化时相邻时段的相角或功率波动。为了展示鲁棒优化对于提高联络线的外特性平稳程度的有效性，将无优化和鲁棒优化的计算结果进行了比较，首先对比了优化前、后的相角波动情况，如图3 所示。图中，相角波动和δ1、δ2均为标幺值，后同。

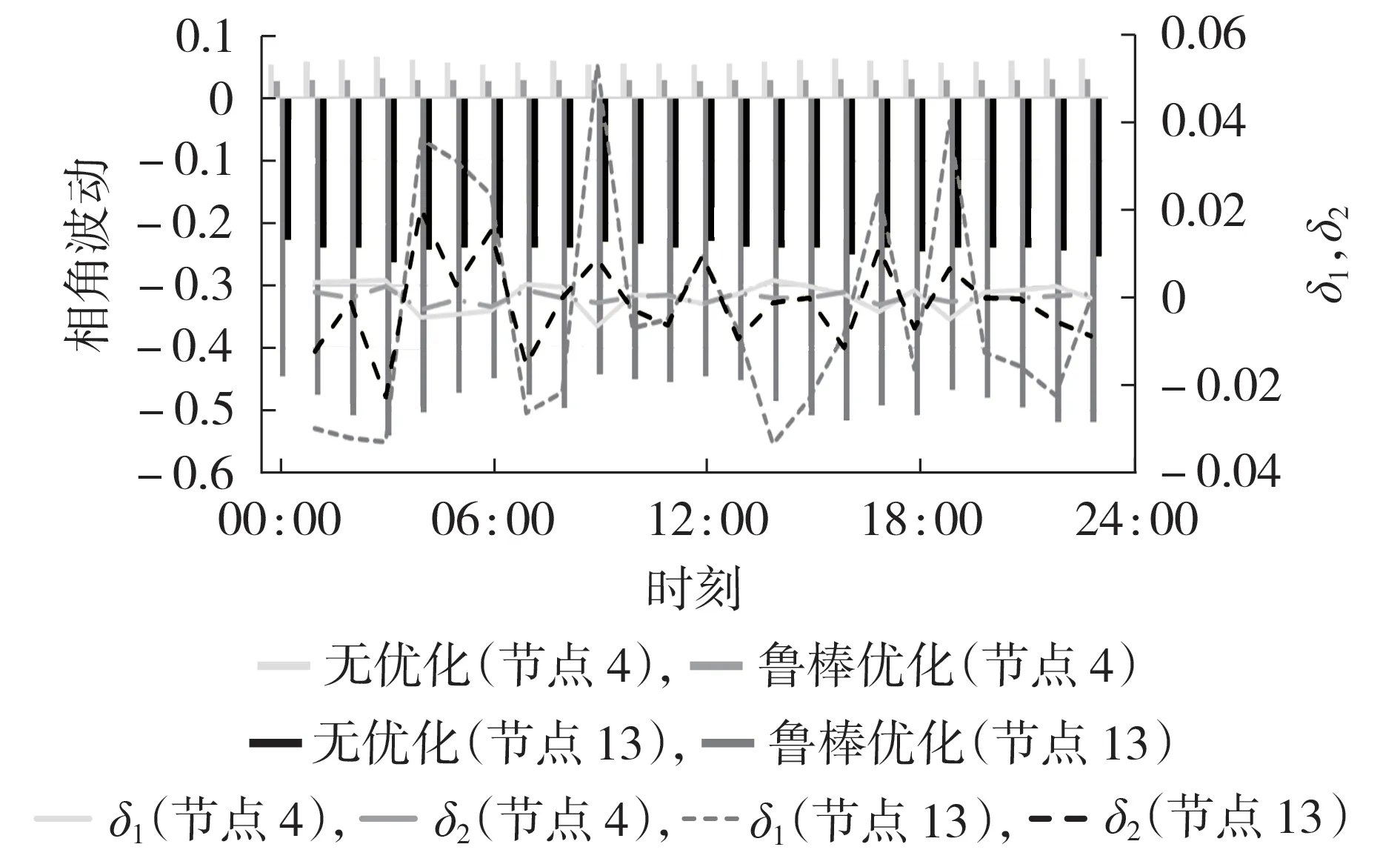
图3 节点4和节点13优化前、后相角波动对比Fig.3 Comparison of phase angle fluctuation before and after optimization of Bus 4 and Bus 13

由图3 可得，与无优化时相角波动大小相比，采用鲁棒优化时联络线节点相角波动更为平缓。在24 h 内，无优化时节点4 和节点13 的相角均值为采用鲁棒优化时的2.01 倍，δ2均明显小于δ1，即采用鲁棒优化时相邻两时段的相角波动小于无优化时计算结果，且在10:00，δ2和δ1相差最大为5.38×10-3p.u.。仿真结果表明，本文所提算法通过合理地控制发电机AGC 的参与因子大小，可以有效降低新能源波动对联络线节点电压相角的影响。

由式（13）可知，联络线节点相角变化量除以联络线串联电抗，近似反映了联络线功率波动。在联络线电抗值不变的条件下，当联络线两端相角的波动减小时，说明交换功率波动减小。据此，图4 对比了2 条联络线上优化前、后的功率波动情况。图中，功率波动为标幺值。

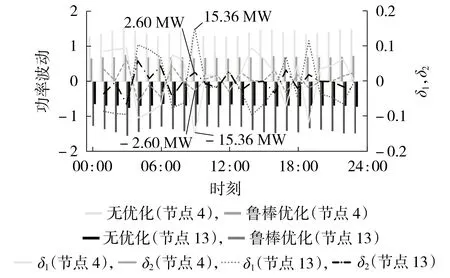
图4 节点4和节点13优化前、后功率波动对比Fig.4 Comparison of power fluctuation before and after optimization of Bus 4 and Bus 13

由图4 可得，采用鲁棒优化时的功率波动明显小于无优化时的功率波动。在09:00—10:00 时段，无优化和鲁棒优化下的功率波动绝对值最大，分别为15.36 MW 和2.60 MW，采用鲁棒优化仅为无优化的16.93%。仿真结果表明鲁棒优化在新能源出力不确定情况下，对外特性的稳定性具有明显改善效果。

为了进一步验证本文所提算法的有效性和可行性，对IEEE 118 节点测试系统进行仿真分析。本文将IEEE 118节点测试系统划分为区域1和区域2，以区域1 为观测区域，其节点15 和节点19 为观测点。区域之间设有2条联络线，第一条联络线为区域1的节点15 和区域2 的节点33 相连接，第二条联络线为区域1 的节点19 和区域2 的节点34 相连接。图5 展示了节点15 和节点19 相角波动情况，而节点15 和节点19功率波动情况如附录A图A2所示。

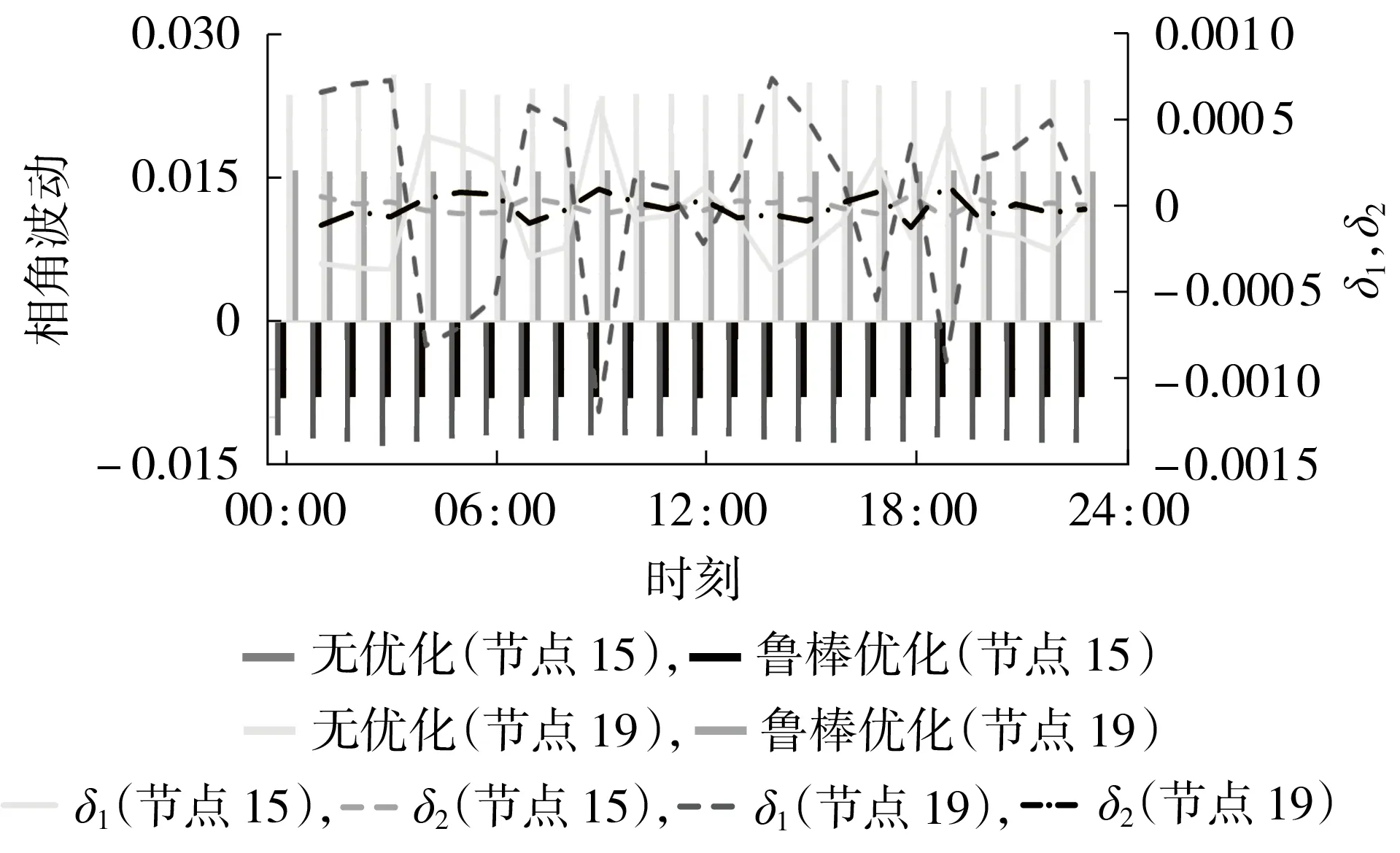
图5 节点15和节点19优化前、后相角波动对比Fig.5 Comparison of phase angle fluctuation before and after optimization of Bus 15 and Bus 19

通过观察图5 和图A2 可知，与无优化时的计算结果相比，采用鲁棒优化计算得到的联络线节点相角和节点功率波动都更为平缓，这表明本文所提算法同样适用于IEEE 118 节点测试系统。为了进一步体现算法的优越性，计算双IEEE 14 节点系统和IEEE 118节点测试系统δ的标准差，计算结果保留3位小数，如表1所示，表中相角为标幺值。

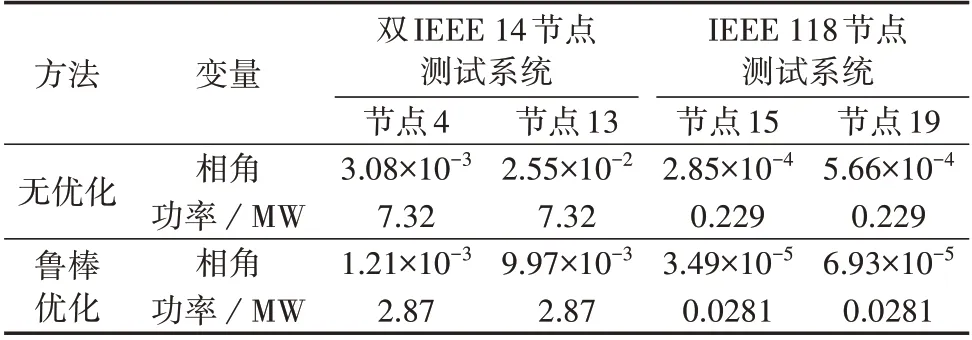
表1 2个测试系统有、无鲁棒优化对外特性计算结果比较Table 1 Comparison of calculation results of external characteristics for two test systems between with and without robust optimization

由表1 可得，采用鲁棒优化计算得到的相角和功率的δ标准差都远小于无优化时的计算结果，进一步验证了本文所提算法的可行性和普适性。