拨动式上变频压电俘能器的设计与研究

吴新雅，董维杰

(1.大连理工大学 电子信息与电气工程学部，辽宁 大连 116024；2.大连理工大学 电气工程学院，辽宁 大连 116024)

0 引言

随着5G技术的开发和应用，“万物互联”正在逐渐变成现实，为物联网络中大量的传感器节点和低功耗电子设备供电，已成为研究的热点。利用传统电池供电，面临着污染环境、电池更换等一系列技术和人力层面的问题，因此,收集环境中能量的自供电技术更符合环保理念。环境中存在着大量的低频振动能量，工业设备、运输车辆及机械设备等产生的振动能量多集中在10 Hz甚至5 Hz以下。压电振动俘能器在固有频率处的功率输出最高，且输出功率与固有频率正相关，而压电俘能器固有频率一般在几十、上百赫兹，若仅降低压电振荡结构的固有频率，则必须增大结构等效质量，减小刚度，但这样易导致结构损坏，且输出功率不易满足供电需求。针对低频、超低频振动能量收集，上变频压电俘能器[1]成为一个重要的研究方向。

上变频压电俘能器通常分为辅助结构和压电结构两部分，辅助结构将低频环境振动转化为压电结构的高频振动，使压电结构在高频谐振响应时产生更高的输出功率。上变频压电俘能器可分为接触式激励和非接触式激励，其中接触式激励分为碰撞式激励[2]和拨动式激励[3]。接触式激励中辅助结构与压电结构接触并迅速分离，两者相对位置不变的为碰撞式激励，两种相对位置交换的为拨动式激励，在接触时间内产生较大的瞬态力，使得压电结构在其较高的固有频率处做自由衰减振动以实现上变频。文献[4]采用蜂鸣片在其上下位置设置阻挡块，当受到垂向振动激励时，蜂鸣片与阻挡块碰撞产生一个大的瞬态力，从而实现上变频，在1g(g=9.8 m/s2)的激励和最佳负载匹配时，输出功率可达0.8 mW。文献[5]采用旋转拨片结构对压电悬臂梁进行激励，基于哈密顿原理和赫兹接触原理对系统进行综合建模。其虽未提出新型的上变频压电俘能器结构，但为拨动式上变频俘能器的开发提供了思路。文献[6]利用圆柱滑块突起拨动压电悬臂梁前端质量块，避免了直接碰撞悬臂梁，重点讨论了质量块的形状和碰撞接触面的设计对功率输出的影响。实验证明，非对称接触面相比于对称接触面的输出功率提高了约23%。非接触式激励包括磁致上变频[7]、惯性致上变频[8]及内共振致上变频[9]等。其中利用惯性实现上变频与接触式类似，俘能器在振动位移最大处受到辅助结构的位移限制而产生较大的瞬态力，并使压电结构产生大的形变，在其固有频率处做自由衰减振动以实现上变频。利用永磁体可在1个周期内实现多次激励而实现上变频[10]，也可利用磁场的非线性来实现上变频，如磁力引入了位移的立方项，实现1∶3的变频效果[11]。文献[12]利用弹簧摆结构的一个摆动周期提供两次往复力，实现内共振达到1∶2的变频效果。由此可见，利用内共振和磁力的方式实现上变频，其变频比不高，有时无法满足实际需求。

本文基于赫兹接触理论提出了一种收集垂向低频振动能量的拨动式上变频压电俘能器，对其基本结构、工作原理进行理论分析，并对系统进行动力学建模。测试了该俘能器的低频振动能量收集性能，探究了拨片厚度、拨片与悬臂梁重叠长度对系统功率输出的影响，为低频振动能量收集提出了一种可行的解决方案。

1 上变频压电俘能器的理论分析

1.1 单自由度结构的振动功率分析

上变频压电俘能器中压电结构属于单自由度结构，首先对压电结构进行集总参数建模，并对其输出功率与频率的关系进行理论分析和研究。单自由度压电结构可等效成弹簧-阻尼-质量块-压电集总参数模型，如图1所示。图中，m为悬臂梁顶端的等效质量，y(t)为振动源激励随时间变化的位移函数，x(t)为质量块随时间变化的位移函数，k为系统的等效刚度，cm为系统的机械阻尼系数，ce为系统的电致阻尼系数，将压电输出表示为电致阻尼，电致阻尼将机械功率转化为电功率。

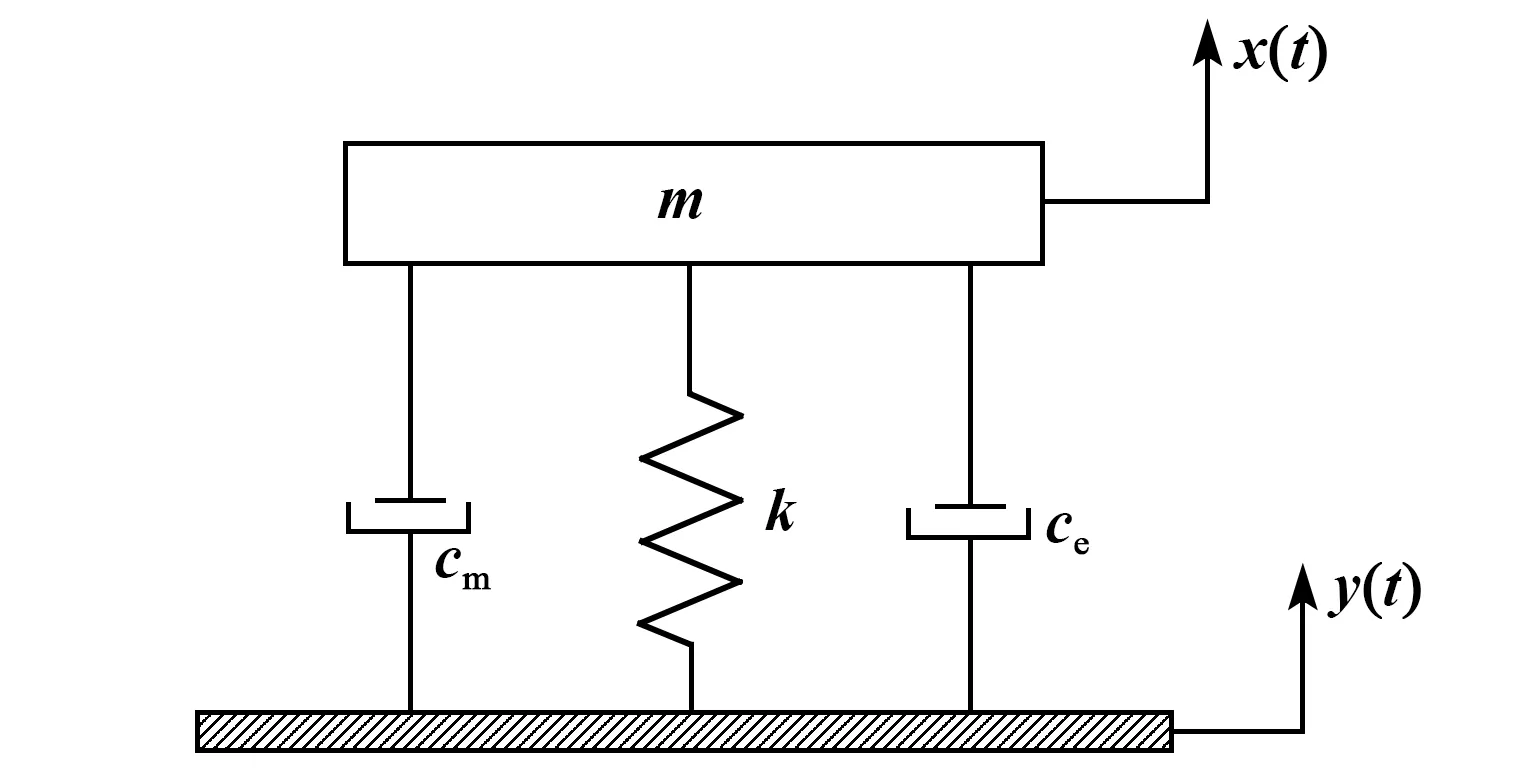
图1 单自由度压电结构集总参数模型

理想振动体振动位移y(t)为正弦振动激励，即y(t)=Ysin(ωt)，压电悬臂梁动力学方程为

(1)

式(1)的解为

Ysin(ωt-φ)

(2)

式中ω为激励频率。

根据能量守恒定律，电致阻尼所消耗的能量是系统的输出能量，即系统转化为电能，所以系统输出的瞬时电功率为

(3)

将式(2)代入式(3)并整理得：

(4)

当环境中的激励频率ω等于系统的固有频率ωn(ω=ωn)时，系统输出电功率Pe取得最大值，即：

(5)

由式(5)可知，系统电功率输出与频率的三次方正相关。对于低频振动激励，压电悬臂梁本身获取功率小，通过辅助机构把环境的低频激励转化为高频激励，可提高功率输出。

1.2 上变频压电俘能器接触理论分析

传统压电俘能器直接吸收环境振动激励，本文提出的拨动式上变频压电俘能器通过辅助结构吸收环境中低频振动能量，再通过拨片对压电悬臂梁施加激励，将能量传递给压电悬臂梁，压电悬臂梁以较高的本征频率释放能量，从而实现上变频效果。图2为上变频压电俘能器原理。其主要由压电悬臂梁、辅助结构组成，通过辅助结构的垂向运动，拨片与压电悬臂梁接触并使其受迫形变直至脱离，拨片选用矩形且前端进行打磨，以实现降低系统阻尼的目的。

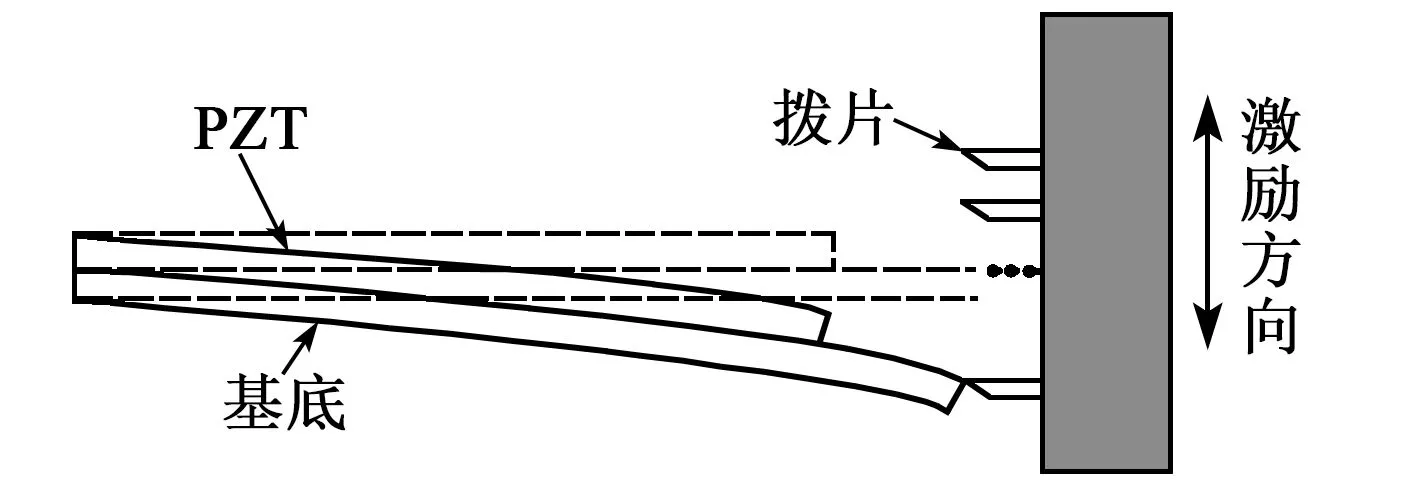
图2 上变频压电俘能器原理图

根据赫兹接触理论及Fu等[13]的相关研究，假设辅助结构的质量无穷大，此时悬臂梁所受冲击满足赫兹接触原理，并对拨片与压电悬臂梁接触时的瞬态力进行具体分析。在1个周期内，根据悬臂梁所受的冲击次数，将激励方式分为单冲击和多冲击式，压电悬臂梁与拨片接触时间tc是一个非常重要的参数：

(6)

式中：xd为分离时悬臂梁的位移，v0为拨动速度。

接触时间受到激励频率和辅助结构整体位移大小的限制，当拨片与悬臂梁接触时，根据赫兹接触原理，接触力Fc与局部压痕δ正相关：

(7)

(8)

(9)

式中：κc为赫兹接触刚度；E为接触材料的等效弹性模量；E1，E2分别为拨片和压电悬臂梁的弹性模量；λ1，λ2分别为拨片和压电梁的泊松比；R为接触时拨片与压电悬臂梁的等效曲率半径；R1，R2分别为拨片和压电悬臂梁接触时各自的曲率半径。

由于在俘能器运行过程中压电悬臂梁不断受到不同拨片的冲击作用，局部压痕δ(t)为

δ(t)=z(t)-xi(t)

(10)

z(t)=v0t

(11)

式中：z(t)为接触过程中拨片的位移；xi(t)为不同拨片引起的压电悬臂梁的位移。因此，压电悬臂梁在运行过程中所受接触力Fc(t)为

(12)

在设计拨动式上变频压电俘能器时，要求接触力在压电梁承受的范围内尽量大，依据式(8)、(9)合理增大接触刚度，应合理选取拨片和压电梁的材料及二者的重叠长度，等效弹性模量和等效刚度尽量大。

1.3 上变频压电俘能器结构动力学分析

根据以上理论分析，结合环境中大量存在的大型振动设备振动频率低及振幅小的特点，如炼钢厂中结晶器振动频率为4～5 Hz，为实现上变频的工作模式，辅助结构中设计了弹簧振动平台作为振动位移放大装置，安装多个拨片实现1个周期多次激励，上变频压电俘能器整体结构如图3所示。辅助结构主要有2块140 mm×140 mm×4 mm的亚克力板，分为底板和盖板，其中底板固定，4个弹簧支撑上盖板为使辅助结构在低频共振时产生大的位移，上盖板安装质量块以降低辅助结构的固有频率来适应环境中低频振动激励。压电结构为50 mm×40 mm×0.8 mm的矩形悬臂梁，固定在底板上。拨片选取不锈钢材质经垫块固定后安装在上盖板上，通过拨片上下运动时与压电悬臂梁的接触实现上变频。

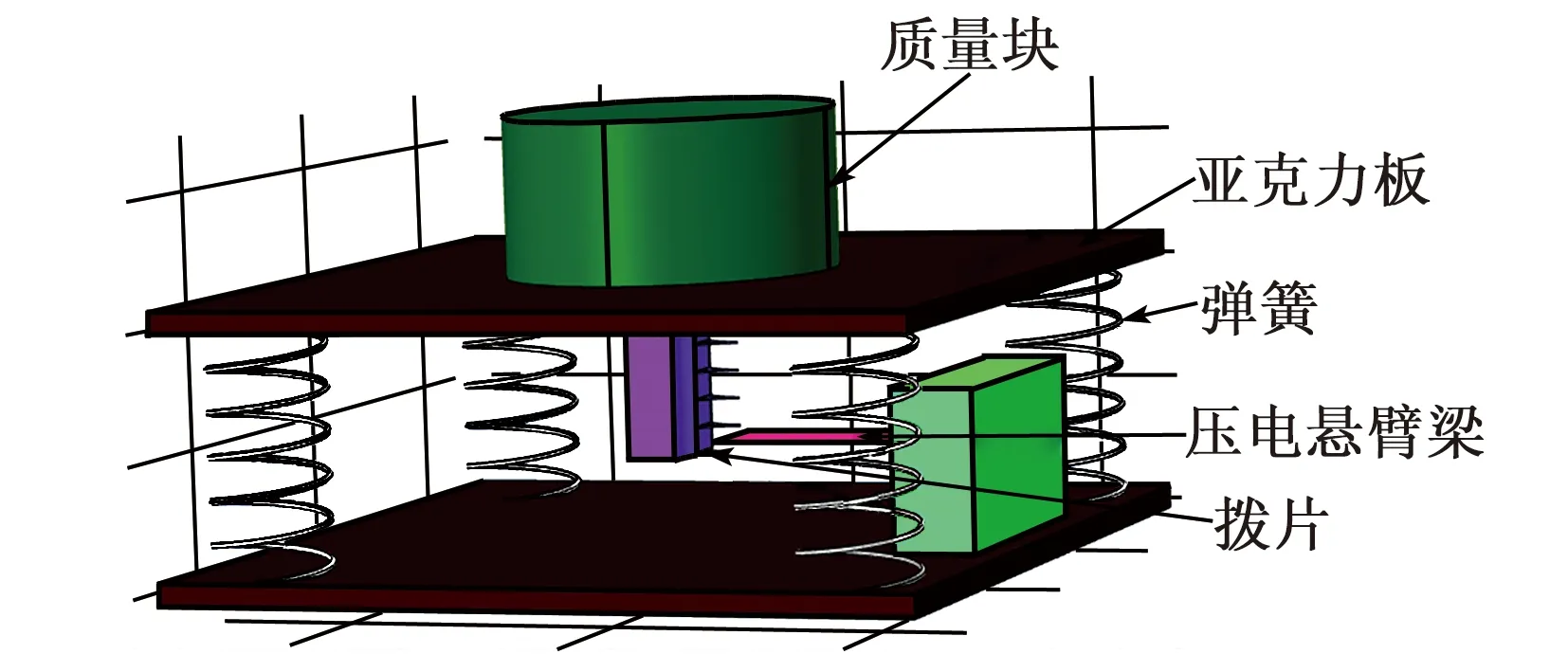
图3 上变频压电俘能器结构示意图

图4为上变频能量收集系统的动力学集中参数模型。图中，m1、m2分别为压电悬臂梁的等效质量和辅助结构等效质量，k1、k2分别为悬臂梁的等效刚度和辅助结构的等效刚度，c1、c2分别为悬臂梁的等效阻尼和辅助结构的等效阻尼，α为机电耦合系数，x(t)、z(t)分别为压电悬臂梁和辅助结构的动态位移，该系统中电致阻尼等效为压电输出，V(t)为输出电压。

图4 上变频压电俘能器集中参数模型

一个低频振动周期中的一次拨动分为两个工作过程：

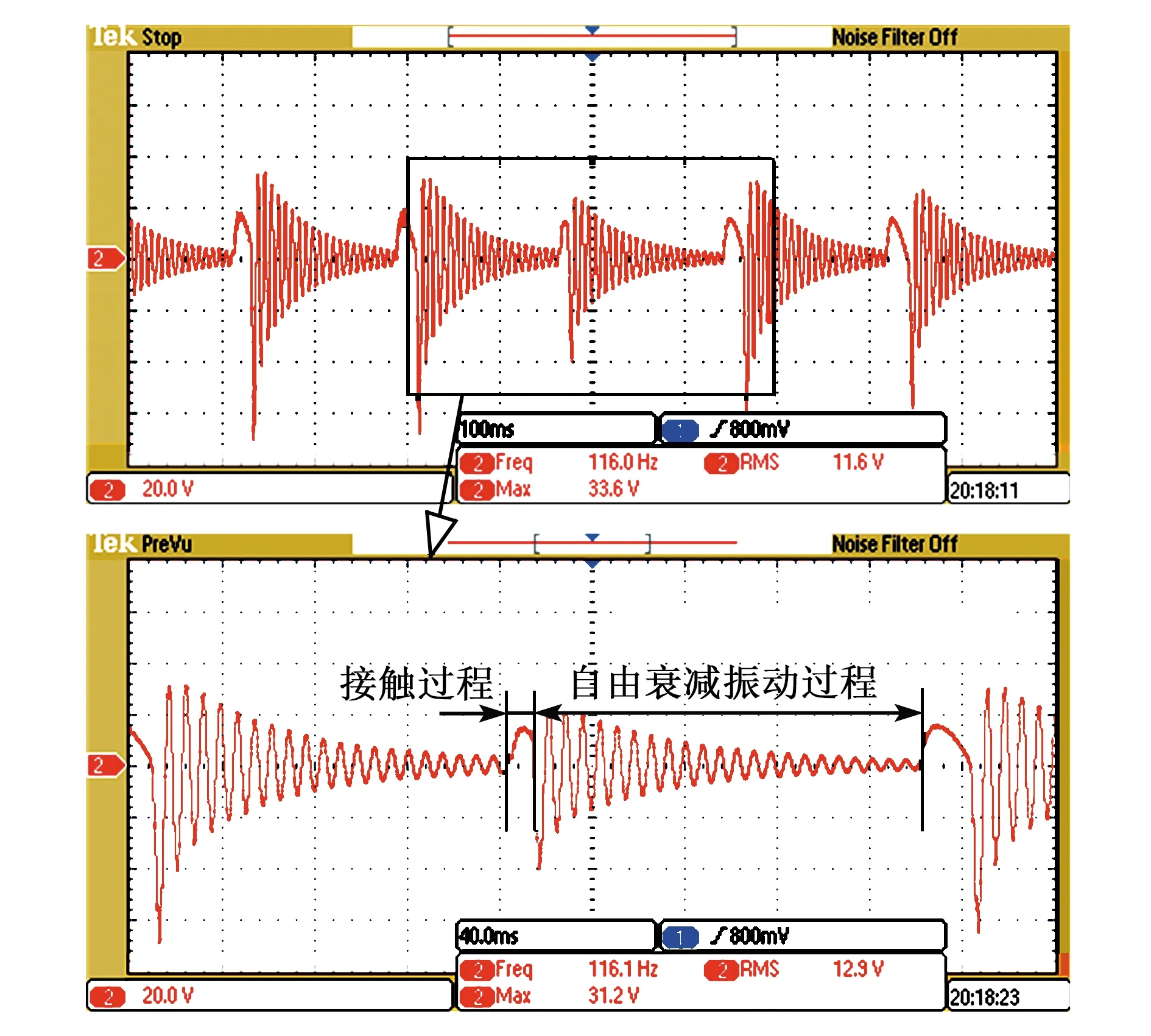
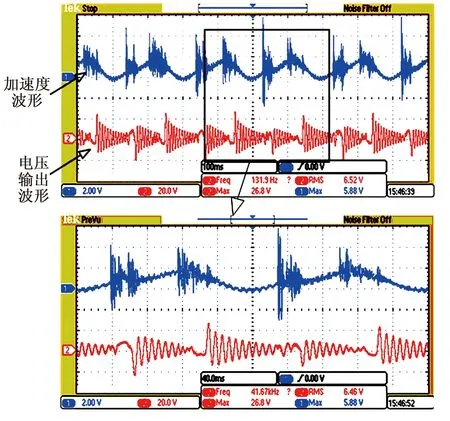
1) 0

(13)

式中i表示第i次拨动。

2)t>tc。压电悬臂梁与拨片分离后具有初速度，在拨片之间的间隙内以固有频率做自由衰减振动，此时式(13)中接触力项变为0，压电悬臂梁将接触时获取的机械能转化为电能。如果辅助结构位移大或旋转连续位移，可设置多个拨片，压电梁衰减振动6～7个周期时被再次拨动，可保持输出电压幅度衰减小。

2 实验验证

图5为上变频压电俘能器实验平台。由Tektronix AFG 3021B信号发生器输出一个正弦小信号，其经功率放大器放大后输入给激振台，从而输出一个对应频率的振动激励来模拟环境激励。采用CA-YD-127型压电加速度传感器经电荷放大器放大后输出电压信号，用示波器测量盖板的振动加速度。实验选取Midé公司V25W型号的双晶压电悬臂梁，双晶压电片并联连接，以精密电阻箱作为输出负载，对该压电片进行负载功率输出特性实验发现，匹配负载约为14 kΩ。

图5 上变频压电俘能器实验平台

图6为上变频压电俘能器结构。经过实验测试，当激振台振动位移为3～4 mm时，无论有无压电悬臂梁，弹簧振动平台振动位移约为10 mm。

图6 上变频压电俘能器结构

2.1 拨动式上变频压电俘能器能量收集实验

拨片与压电悬臂梁的接触过程包括撞击、滑动及脱离3个阶段，整个过程中压电悬臂梁为受迫运动。分离后压电悬臂梁以较大的位移自由衰减振动。因此，多拨片激励时，拨片间的间距不能过小，否则压电悬臂梁在脱离前一个拨片后可能与下一个拨片发生碰撞，影响整个结构的能量输出。经过实验可知，压电悬臂梁自由衰减振幅约2 mm，拨片间距为4～5 mm较合理。由于辅助结构位移的限制，能量收集实验只测试了单拨片和双拨片激励两种情况。调整辅助结构顶端质量块质量使辅助结构谐振，拨片厚为0.1 mm，拨片与悬臂梁的重叠长度2 mm，在1g、5.67 Hz单拨片激励下，压电悬臂梁的输出电压如图7所示，平均输出功率约9.6 mW。无质量块V25W压电悬臂梁一阶固有频率为120 Hz，变频比约为1∶21。

图7 单拨动式上变频压电俘能器输出电压波形

压电梁自由衰减振动后期输出电压幅值较低，通过增加激励次数提高该时段的电压幅值。双拨动式上变频压电俘能器加速度和电压波形如图8所示。通道1为加速度计的输出电压，均方根值约为1g(1 V对应1g)，但在拨片与悬臂梁接触时加速度会突增，瞬时加速度为3g～5g，输出功率约3 mW。与单拨动式上变频压电俘能器相比，双拨动上变频压电俘能器一个振动周期拨动2次，输出电压幅值更均匀，输出功率下降，主要是由于拨片数量的增加增大了系统的阻尼，在俘能器工作过程中能量损失增加。在大振动激励环境中，双拨动式压电俘能器的效果优于单拨动式，此外拨动时压电悬臂梁振动方向和振动速度对输出电压有正或负的影响。

图8 双拨动式上变频压电俘能器加速度及输出电压波形

2.2 重叠长度和拨片厚度对能量输出的影响

实验过程中发现，压电悬臂梁与拨片的重叠长度对功率输出和变频效果影响很大。在拨片与压电悬臂梁接触长度逐渐增大的过程中,接触时间逐渐变大，当接触时间变为压电悬臂梁振动的半个周期时，压电悬臂梁输出电压波形如图9所示。

图9 重叠长度过大时压电悬臂梁输出电压波形

由图9可知，整体结构变频比由原来的1∶21降低到1∶9，且高频部分电压幅值过低,局部幅值小于2 V，导致后接能量管理电路无法得到有效利用。因为重叠长度变大，则需要更大的激励能量，压电悬臂梁的受迫形变和位移也将变大，过高的激励易使压电梁损坏，且系统受辅助结构激励能量和位移幅度的限制，故重叠长度不应过大，上变频压电俘能器工作时应避免此工作模式。

本文研究了拨片厚度对功率输出的影响，分别选取厚为0.02 mm、0.03 mm、0.04 mm、0.05 mm、0.06 mm及0.1 mm的拨片进行实验，压电梁输出功率随拨片厚度的变化如图10所示。

图10 输出功率随拨片厚度的变化

由图10可知，俘能器输出功率随拨片厚度增加而增大，这是因为拨片厚度的增加增大了式(7)中等效曲率半径，进而接触力增大。但随着拨片厚度的增加，拨片自身刚度也会增加，由于瞬间接触力很大，过大的刚度更易损坏压电悬臂梁。在重叠长度相同的情况下，压电悬臂梁的功率输出不会一直增加。综上考虑，建议选取拨片厚度为0.1 mm。

3 结束语

本文针对低频振动能量收集功率低的问题，提出了一种基于弹簧振动平台位移放大的拨动式上变频压电俘能器的新型结构。弹簧振动平台可有效地吸收环境中低频小位移振动能量，并将其转化为上盖板和拨片的大位移振动，拨片拨动压电悬臂梁，激励压电高频谐响应，从而提高压电悬臂梁在低频环境激励下的能量收集效果。通过理论分析说明了高频振动激励下压电悬臂梁可输出更高的功率，根据赫兹接触理论说明了拨片与压电悬臂梁接触时产生的瞬态力。通过实验对比分析了压电梁、拨片重叠长度及拨片厚度对压电悬臂梁输出功率的影响，确定了矩形不锈钢拨片厚度为0.1 mm。实验表明，在1g、5.67 Hz的激励下，单拨动式上变频压电俘能器输出功率为9.6 mW。多拨动式上变频压电俘能器更适合大激励环境。本文提出的弹簧振动平台可作为开发平台，除接触式上变频工作模式外，同样支持非接触式工作模式，有待继续研究开发；弹簧振动平台由4个弹簧进行支撑，工作过程易出现振动不稳定，仍有改进的空间。