适用于宽带滤波器的I.H.P.SAW基底结构优化设计
2022-11-18孙晓红张晓东杨以俊
孙晓红,张晓东,杨以俊
(苏州科技大学 电子与信息工程学院,江苏 苏州 215009)
0 引言
高质量的无线通信要求滤波器具有小纹波、低插损、优良的频率选择能力以及出色的带外抑制能力[1]。声表面波(SAW)滤波器[2]因体积小、隔离性好而被广泛应用于射频信号处理系统中,但与体声波(BAW)滤波器相比,传统的SAW器件在带宽、频率稳定性及高频性能方面呈现一定劣势[3]。近年来,人们提出了超高性能(I.H.P.)SAW器件结构[4],并通过实验证实其具有高品质因数(Q)值、优异的频率稳定性和良好的散热性能,这意味着采用I.H.P. SAW器件设计的滤波器在性能上可超越BAW器件。为进一步探索I.H.P. SAW器件在宽带滤波器应用中的适用性,本文对器件各层厚度进行了优化,以寻求可获取最大滤波器带宽的基底结构设计。基于有限元/边界元法(FEM/BEM)[5]基本原理,考虑包括质量加载效应[6-7]在内的声与电相互作用关系,通过采用修正的多层复合格林函数以及谐振器导纳计算,结合改进的收敛算法实现了对LiNbO3多层I.H.P. SAW器件精确、快速的计算。基于半无限器件结构的假设,开展对电极厚度(tCu)、压电层厚度(tLN)和功能层厚度(tSiO2)的三维优化。利用广义格林函数的特征,将三维优化变量降为二维优化,以获取最优的tLN与tSiO2组合。进一步研究谐振器导纳的频域变化特征,获取最优的tCu,从而寻求适用于宽带滤波器的I.H.P. SAW基底结构的设计。
1 器件与模型假设
T.Takai等通过实验证明了两层I.H.P. SAW器件与三层结构呈现相似的性能[4],因此,本文对两层结构器件展开研究,结构如图1所示。第一层为5°LiNbO3压电层,用于获得更好的高频性能。第二层为SiO2功能层,用于改善谐振频率的温度稳定性[8]。金属电极采用Cu材料,有利于将波导能量限制在其下方,适用于高功率应用场景[9]。衬底采用硅(Si)材料,为简化运算,可将其简化为半无限厚度结构。结构周期为2 μm,金属化比为0.5,反射栅指条数为20,换能器指条数为141,孔径为∅400 nm。

图1 两层 I.H.P. SAW器件结构截面图
2 FEM/BEM数值计算法
考虑电极的质量加载效应,将格林函数与FEM/BEM相结合,采用切比雪夫多项式对电极上的电荷与应力分布进行建模,以更精确地描述器件的特性[6]。此外,根据边界连续性原理对多层结构的格林函数进行修正,从而可获取谐振器的导纳矩阵、电极,以及压电层界面的应力、自由电荷、位移和电势等场分布结果。
2.1 控制方程
在图1所示的坐标系下,位移矢量u(x)和电势φ(x)的卷积形式:
(1)
式中:G(x)为4×4的矩阵的广义格林函数;ts(x)为应力向量;σ(x)为自由电荷密度。考虑到非均匀分布特征的影响,第j根电极上的应力和自由电荷密度可用第一类切比雪夫多项式表示为
(2)
式中:Nj为多项式计算展开的项数;cj为电极的中心坐标;aj为电极的半宽。采用变分迭代法将积分方程简化为线性方程组,结合电路理论,易推出导纳矩阵。
2.2 边界条件
结构内部的所有界面均假设为完美匹配。应力、电势在z向上连续,电极和压电层界面处可表示为
(3)
在界面z=0处,电荷分布等于法向上电位移的差,有
Dz(x,z)|z=0--Dz(x,z)|z=0+=σ(x)
(4)
对于此多层结构的I.H.P. SAW器件,需要注意对单层格林函数进行修正,即为了满足连续性边界条件,应以第二层(SiO2功能层)格林函数作为上层结构的边界限制条件,以此推算多层复合的格林函数。
3 计算结果与讨论
器件的谐振特性与tLN,tSiO2,tCu因素有关。为了更快优化基底结构尺寸,利用格林函数的特性将三维优化变量降为二维变量,一旦找到tLN和tSiO2的最佳组合,结合导纳特性寻找最优tCu,从而获得宽带设计的最佳尺寸参数。
3.1 广义格林函数
格林函数反映了半无限大电介质表面上激发源分布与场分布之间的关系。慢度域中,广义格林函数与频率无关,与电极厚度无关。通过分析格林函数与慢度的变化关系,寻求峰谷点慢度间隔更宽的结构尺寸,可用于设计更大带宽的滤波器。
设置tCu=80 nm,计算1 GHz下的有效介电常数。图2为有效介电常数(Eps)与慢度的变化关系图。有效介电常数与格林函数的转换公式为
(5)
式中k为波数。

图2 有效介电常数与慢度关系
由图2(a)可见,随着tLN的增加,Eps曲线向更大慢度值方向移动。相对于谷值,Eps峰值对应的慢度位置变化更敏感,从而在谷峰值之间形成了变化的慢度差。当tLN值持续增加时,峰值所对应的慢度最终将达到稳定,谷峰值之间慢度间隙将减少。tSiO2对Eps产生的影响如图2(b)所示,其趋势与tLN相同。
为寻求最合适的tLN、tSiO2尺寸,设置tLN以100 nm的步长从200 nm变化到1 000 nm,tSiO2以100 nm的步长从100 nm变化到800 nm。对72(9×8=72)种案例尺寸进行格林函数计算,并对谷峰值慢度间隙进行统计。计算的慢度间隙结果如图3所示。由图可以看出,在800 nm(0.2λ,其中λ为电周期)的tLN和600 nm(0.15λ)的tSiO2尺寸下可获得最大慢度间隙为3.05×10-5s/m。

图3 慢度间隙与tLN,tSiO2之间的关系
3.2 谐振器导纳特性
谐振器的导纳变化直观地展示了谐振器器件的频响特性。设置tLN=800 nm,tSiO2=600 nm,tCu以30 nm的步长从30 nm变化到270 nm,研究谐振频率点的变化。图4(a)显示了以1 MHz为步径,I.H.P. SAW谐振器导纳的详细计算结果。随着tCu的增加,谐振频率与反谐振频率点都将减小。图4(b)进一步统计了谐振点与反谐振点之间的频率差。由图4(b)可见,当金属厚度为150 nm(0.037 5λ)时,谐振器的谐振频率可获得最大为138 MHz的频率间隙(中心频率为949 MHz),此时谐振点为880 MHz,反谐振点为1 018 MHz。

图4 电极厚度造成的影响
3.3 基底优化尺寸下的场分布特性
由上述分析可知,优化尺寸为0.15λ的tSiO2、0.2λ的tLN和0.037 5λ的tCu的I.H.P SAW基底结构,可获得最大的谐振点-反谐振点频率间隙,其导纳特性如图5所示。880 MHz为其谐振峰,而在819 MHz处产生弱谐振峰。图6描述了此两个频率点的位移矢量场分布情况。由图6(a)可见,y方向上的位移矢量值远大于其他两个分量,这意味着在880 MHz频率下可以获得SH波。但在弱谐振点,x方向的水平位移分量占主导地位,如图6(b)所示,这意味着在819 MHz频率点出现的是瑞利波,此频率点远离此时的中心频率点,因而对带内信号不会产生干扰。
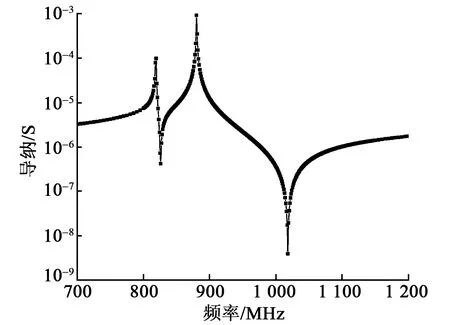
图5 优化尺寸的I.H.P. SAW器件导纳特性

图6 位移矢量分布
4 结束语
研究了两层I.H.P. SAW器件衬底结构层厚对谐振器性能变化的影响。采用FEM/BEM分析方法,借助多层复合的格林函数与谐振器的导纳特性进行分析。对金属化比为0.5,结构周期为2 μm的器件,采用0.15λ厚度的SiO2、0.2λ厚度的5°LiNbO3以及0.037 5λ厚度的金属Cu电极,其谐振点(880 MHz)与反谐振点(1 018 MHz)间具有最大频率差(138 MHz)。该结论为适用于宽带滤波器的I.H.P. SAW器件设计提供了参考。
