电磁寄生参数在高频SAW滤波器设计中的应用

黄小东，黄 玮，魏勇平，闫坤坤，李玉龙，苗 湘，陈 发，徐 巍，蒋元军,罗 为,4

(1.华中科技大学 光学与电子信息学院，湖北 武汉430000；2.北京中科飞鸿科技股份有限公司，北京100095；3.华中科技大学 武汉光电国家研究中心，湖北 武汉430000；4.深圳华中科技大学研究院，广东 深圳518000)

0 引言

随着5G通信技术的迅速发展，其频谱资源日益紧张。例如5G频段的n3频段号上行频率为1 710～1 785 MHz，下行频率为1 805～1 880 MHz，上行与下行频率间距仅为20 MHz。开发满足此类条件的声表面波(SAW)滤波器的难点在于既要保证器件的通带带宽(75 MHz)和低插入损耗，又要保证高的矩形系数。在多种SAW滤波器结构中，梯形结构因带宽大，插入损耗小，可小型化而受到关注[1]。未考虑封装和汇流条的电磁寄生参数而设计的小型化封装的高频SAW滤波器，经实验测试表明,其易出现通带带宽变窄，通带内波动大，通带内驻波大等问题，这进一步增加了滤波器的设计难度。为了解决此问题，本文拟用包含封装和汇流条的电磁寄生参数的等效电路模型，通过电声-电磁联合仿真来设计此类具有低损耗、高矩形系数的高频SAW滤波器。

1 梯形结构SAW滤波器设计

1.1 SAW单端谐振器耦合模(COM)模型仿真

为获得较好的带外抑制和插入损耗，本文采用7阶谐振器级联梯形结构，如图1所示。SAW滤波器的压电材料选择工作在漏波(SH)模式的42°Y-XLiTaO3，金属膜材料为铝。首先通过有限元方法拟合得到耦合模(COM)参数，并通过工艺结果进行校正；再通过COM方程计算谐振器的P矩阵，并得出谐振器的导纳[2-3]。以上部分为模拟SAW滤波器中的电声转换。

图1 梯形结构SAW滤波器示意图

图2为计算得到的单端口谐振器的导纳-频率响应曲线。由图可见，谐振器的谐振频率(fr)为1 765 MHz，反谐振频率(far)为1 829 MHz。然而在高频情况下，SAW谐振器的导纳还受到封装和汇流条的电磁寄生参数的影响。如图2(a)所示，谐振器串联0.2 nH的电感，引起谐振频率向低频端移动13 MHz；谐振器并联0.4 pF的电容，引起反谐振频率向低频端移动5 MHz，如图2(b)所示。

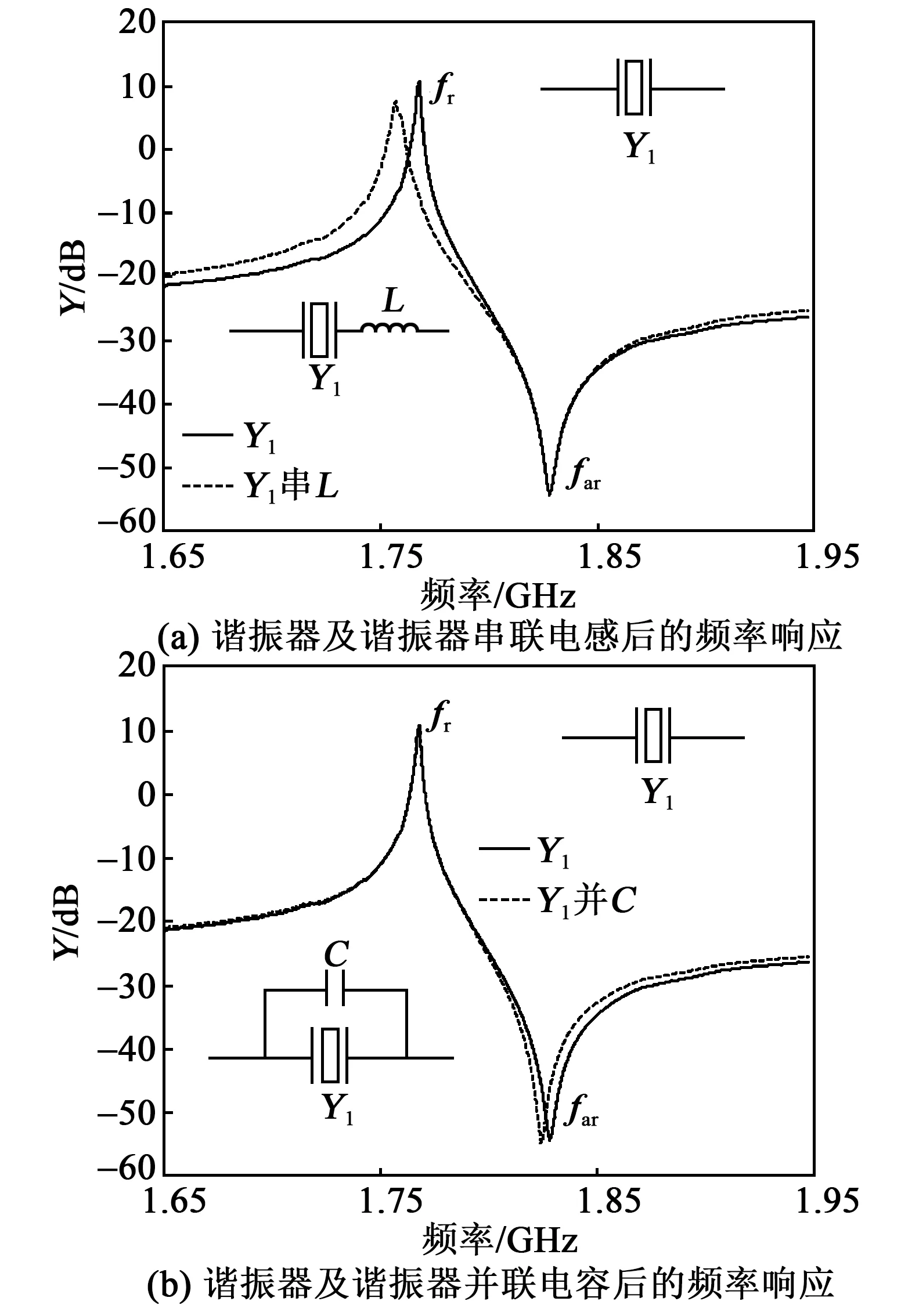
图2 单端口谐振器的导纳-频率响应曲线

1.2 封装和汇流条的电磁仿真及联合仿真

封装及汇流条的电磁寄生参数对谐振器导纳的影响会进一步影响滤波器的性能，为了解决此问题，本文拟建立电声-电磁联合仿真模型。首先，利用HFSS软件建立3.0 mm×3.0 mm封装的3D 仿真模型以计算封装和汇流条的寄生参数，模型包括封装壳、键合线及谐振器之间的汇流条等，如图3(a)所示。模型中所有部件的尺寸根据封装壳厂商提供的图纸绘制，与实际封装的SAW滤波器样品的尺寸一致。模型的材料参数为软件自带的材料参数：封装壳导体部分的材料选择为金，封装壳绝缘体部分的材料为陶瓷；封装壳以上是SAW滤波器芯片，芯片的压电材料部分(立方体)为钽酸锂，汇流条和键合线的材料均为铝；滤波器芯片上的换能器指条全部去除。模型左右各有3根键合线，左边中间和右边中间分别为输入信号键合线和输出信号键合线，其余为接地键合线。计算时，两个集总端口分别放在电信号的流入和流出点。在模型中放入集总端口，计算得到任意两端口之间的S参数，并将其转换为两端口等效电路中的电磁寄生参数，包括电阻(R)、电感(L)和对地电容(C)，如图3(b)所示。通过上述方法可计算得到封装内具有主要影响的电磁寄生参数值。

图3 计算封装和汇流条的电磁寄生参数

将COM模型仿真方法得到的各谐振器导纳参数与上述计算得到的封装和汇流条的电磁寄生参数通过等效电路连接，即建立了电声-电磁联合仿真模型，如图4所示。为简化计算过程，电路为左右对称结构，其中Cb为桥电容，M为互感，左侧L1，R1，C1分别为输入端口到输入焊盘之间(包含信号键合线)的总电感，电阻及对地电容；L2，R2，C2分别为并联臂汇流条的电感，电阻及对地电容；L3，R3分别为接地端口到接地焊盘之间(包含接地键合线)的总电感，电阻；Y1，Y2，Y3，Y4，Y5，Y6，Y7分别为各个谐振器的导纳。在设计过程中，通过模拟退火优化算法得到最佳性能的SAW滤波器的谐振器的孔径、栅周期、指条数和占空比等设计参数。最后，通过半导体工艺制备以上设计参数对应的SAW滤波器，其谐振器局部形貌如图5所示。图中金属指条宽度为499 nm，周期(λ)为2 216 nm，假指长度为1.5×λ，假指与换能器指条间距为0.5×λ。

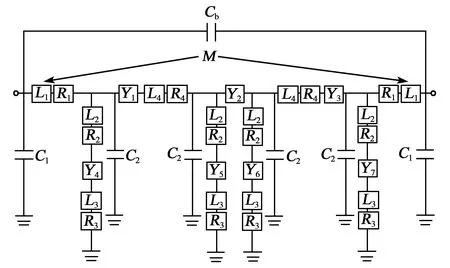
图4 包含封装及汇流条的电磁寄生参数的SAW滤波器等效电路

图5 滤波器的谐振器局部形貌

2 结果分析与讨论

文献中通常报道芯片以外的封装壳的电磁寄生参数对SAW滤波器的影响，忽略了谐振器之间的汇流条的电磁寄生参数[4]。我们认为在高频情况下，汇流条的电磁寄生参数也是设计的关键参数，所以利用图4所示电路对比分析了在设计时考虑和不考虑汇流条的电磁寄生参数的设计方案的模拟结果，以获得汇流条电磁寄生参数对器件性能影响的关系。

图6为汇流条寄生参数对滤波器频响值和驻波产生影响的模拟结果。方案1为考虑封装壳的寄生参数(L1，R1，C1，Cb，M)而不考虑汇流条寄生参数的仿真设计结果。方案2为在方案1的电路中添加图4所述汇流条寄生参数(L2，R2，L4，R4，C2)的模拟结果。由图可知，未考虑汇流条的电磁寄生参数设计方案的仿真结果因受汇流条寄生参数的影响而出现了通带内驻波及波动恶化等问题。其原因在于串联臂汇流条的电感L4(0.2 nH)引起串联臂谐振器的谐振频点向低频端移动，并联臂汇流条的电感L2(0.6 nH)引起并联臂谐振器的谐振频点向低频端移动，汇流条对地电容C2(0.25 pF)导致并联臂谐振器的反谐振频率向低频端移动，以上因素导致滤波器通带阻抗不匹配[4-5]。

图6 汇流条寄生参数对滤波器的S21频响和驻波产生影响的仿真结果

为了获得更好的滤波器性能，我们将图4所示的全部汇流条的寄生参数纳入设计参数中，以解决滤波器研制过程中遇到的通带波动大，驻波大等问题。图7为考虑封装和全部汇流条寄生参数的设计方案(方案3)的仿真结果与实验测试结果。由图可见，实验测试值与仿真设计值吻合较好，表明此仿真模型用于设计高频SAW滤波器的有效性。

图7 考虑封装和汇流条的寄生参数设计的滤波器的仿真和实测频响

3 结束语

经测试，在高频情况下，封装、键合线和汇流条的电磁寄生参数对SAW滤波器的性能有明显影响。本文通过建立包含封装、键合线和汇流条寄生参数的等效电路模型实现了电声-电磁联合仿真，所设计的SAW滤波器可有效避免因封装、键合线和汇流条的电磁寄生参数而引起的滤波器通带波动大，驻波大的问题。所制备的滤波器通带中心频率为1 746.6 MHz，通带内驻波最大值为2.1，最小插入损耗0.87 dB，波动0.5 dB，-1.5 dB带宽75.7 MHz， -3 dB带宽84 MHz (相对带宽为4.8%)，-30 dB带宽112 MHz，BW-3 dB/BW-30 dB矩形系数1.33，带外抑制优于-30 dB。