四种多组分气体拉曼光谱定量计算方法的对比研究

杨申昊，侯春彩，赵韦静，李聪冉，邓 维

（中国船舶集团有限公司第七一八研究所，河北 邯郸 056000）

1 引言

随着拉曼光谱技术的不断发展，拉曼技术在很多领域得到应用。针对气体检测，激光拉曼光谱技术相比于气相色谱、红外光谱技术具有很多优势。相比于气相色谱而言，拉曼光谱技术不需要载气，不需要对混合气体做分离，整个仪器设备装置结构简单，使用维护方便。相比于红外光谱技术，拉曼光谱技术可以检测氮气、氢气等双原子分子，检测的气体种类多，应用场景更为广泛。因此，激光拉曼光谱技术对气体的检测与分析已经成为未来几年最有前景的气体检测技术之一。

在常温常压下，气体拉曼信号十分微弱，容易受到温度、压力、湿度、激光器功率波动、系统热噪声等因素的影响。所以，采用传统的拉曼峰值法、峰面积法进行气体成分定量计算，稳定性、重复性较差，无法满足应用需求。因此，针对气体拉曼光谱定量检测方法的研究已经成为热点问题之一。

2019 年，高颖等[1]针对天然气成分定量检测，提出基于洛伦兹线型的拉曼光谱自动分解算法。2021 年，温国基等[2]提出基于遗传算法与线性叠加模型的混合物组成拉曼光谱分析方法。2016 年，孔德靖等[3]提出采用部分面积法提高气体拉曼光谱测量重复性的方法对10%的C2H2进行验证。2020 年，陈新岗等[4]对变压器油中的溶解气体进行拉曼光谱检测，建立高斯函数模型后，以峰高、半峰宽、峰面积为自变量，气体浓度为因变量建立偏最小二乘回归模型，可以预测气体浓度。针对水溶液中的氯离子，张建新等[5]采用高斯多峰分离技术对重叠的拉曼峰进行分峰拟合，然后采用峰值、峰面积等特征信息与氯离子浓度之间关系进行拟合，氯离子浓度在0.1～4 mg/L 之间线性度较好。2020 年，李光茂等[6]对变压器油中溶解甲醇进行拉曼光谱定量检测，采用最小二乘法将甲醇特征峰强度与甲醇浓度值之间建立线性关系，检测限为15.6 mg/L。2016 年，王乾乾等[7]采用拉曼光谱技术对水溶液中硫酸根离子进行了定量检测，将硫酸根特征峰强度与水分子特征峰强度的比值与硫酸根浓度之间建立了良好的线性关系，进而实现对硫酸根浓度的预测。这种方法与文献[2]中的对某一种气体成分归一化的方法相类似。

遗传算法[8]、谱峰分解[9]、高斯函数模型、分峰拟合等方法主要目的是将混叠的拉曼峰进行分离。分离后，许多文献还是采用传统的峰值、峰面积法建立回归模型进行气体浓度的预测[10-11]。但是，峰值法、面积法对气体浓度预测的重复性较差，无法满足相关行业的标准要求[12]。本文立足于产品的开发与应用，在峰值法、面积法的基础上，提出采用瑞利散射归一化、待测气体成分整体归一化的方法。瑞利散射归一化方法不受待测气体体积分数和为100%的约束，待测气体成分整体归一化可以适用于不同积分时间的情况。同时与文献[2]中某一种气体成分归一化进行对比分析。总结每一种方法的优缺点，为多组分气体拉曼光谱产品化的开发与应用提供参考。

2 实验装置

实验装置结构如图1 所示。实验采用半导体泵浦的二倍频Nd∶YAG（掺铝钇铝石榴石）连续激光器做为激发光源[13]，功率1.5 W。反射镜采用凹面反射镜，直径25.4 mm。收集透镜组与光谱仪之间采用芯径1 mm 光纤进行连接，光谱仪采用1 800 g/mm 透射式光栅光谱仪，探测器采用具有时空累积效应的深度制冷面阵电荷耦合器件进行探测[14]，最低制冷温度可达-70 ℃。激发光通过密闭气室窗口片进入两个反射镜中，在两个反射镜中间实现多次反射[15]。

图1 拉曼光谱仪硬件结构Fig.1 System of the Raman spectrometer

3 结果与讨论

在定量计算之前，采集不同积分时间下多组体积分数为3%的二氧化碳、21%的氧气、76%的氮气组成的混合气体的拉曼光谱数据。不同积分时间下的拉曼谱图如图2(a)所示，图2(b)为拉曼峰的局部放大图。积分时间与幅值呈线性关系，因此，图2 中幅值从小到大对应积分时间依次是：0.1 s、0.2 s、0.3 s、0.5 s、0.8 s、1.0 s、1.2 s、1.5 s、1.8 s、2.0 s、3.0 s、4.0 s，所有数据均30 次叠加。下文定量计算均采用二氧化碳1 386 cm-1特征峰，氧气1 552 cm-1特征峰，氮气2 333 cm-1特征峰。采用二次拟合方式拟合光谱基线，用基线作为待检测气体成分的零点。计算过程中，采用峰值法与三点面积法[3]同时进行计算对比。结果图中peak 为峰值法计算结果，area 为三点面积法计算结果。

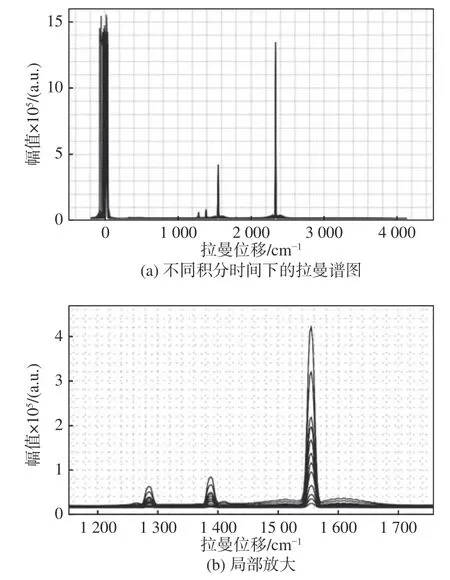
图2 不同积分时间下的拉曼谱图Fig.2 Raman spectra of different integration times

3.1 峰值、峰面积法定量计算结果

选取任一0.1 s 积分时间光谱数据，利用最小二乘法对零点与终点进行直线拟合，得到体积分数与幅值的对应关系式。利用该关系式计算0.1 s 积分时间其他23 组数据，结果见表1。

表1 峰值、峰面积法计算结果Tab.1 Calculation results of peak value and peak area method

采用该组标定系数，计算不同积分时间下的数据，结果如图3 所示。图3 分别为氧气、氮气和二氧化碳在不同积分时间下的数据计算结果。通过图3 可发现，峰值、峰面积计算方法无法适用于不同积分时间的情况。积分时间与峰值、峰面积呈线性关系。

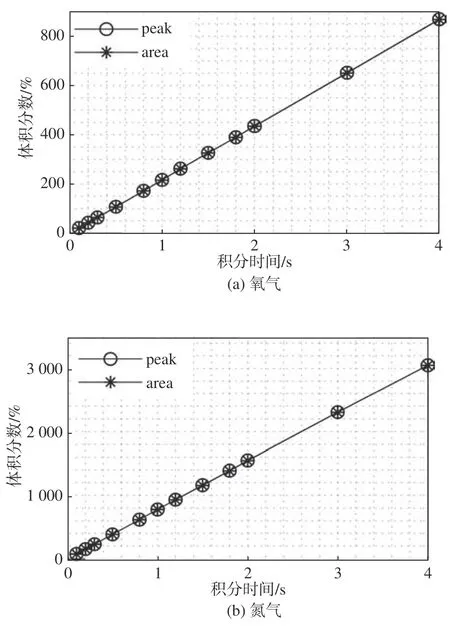
图3 不同气体在不同积分时间下的计算结果Fig.3 Calculation results of gases under different integration times

峰值、峰面积法是拉曼光谱定量计算最简便、最常用的方法，但该方法的稳定性、重复性最差。采用某一积分时间做标定后结果无法适用于不同积分时间的情况，为产品开发带来很多不便。

3.2 瑞利散射归一化

瑞利散射强度R与激光功率成正比，即：

式中：P为激光功率；R为瑞利散射强度；B为比例系数。

某一气体成分的拉曼峰高或峰面积与体积分数成正比[2]，即：

式中：pi表示单位体积分数下第i种气体成分的拉曼峰高或峰面积；ki为正相关系数；ci为气体体积分数；ki与激光功率P呈正相关。式(2)与式(1)相比即可消除激光功率的影响，即：

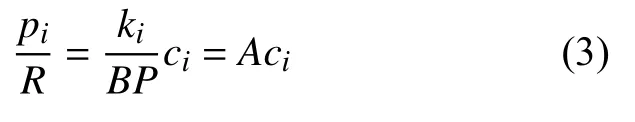
同样对0.1 s 积分时间下的23 组数据进行定量计算，计算结果见表2。

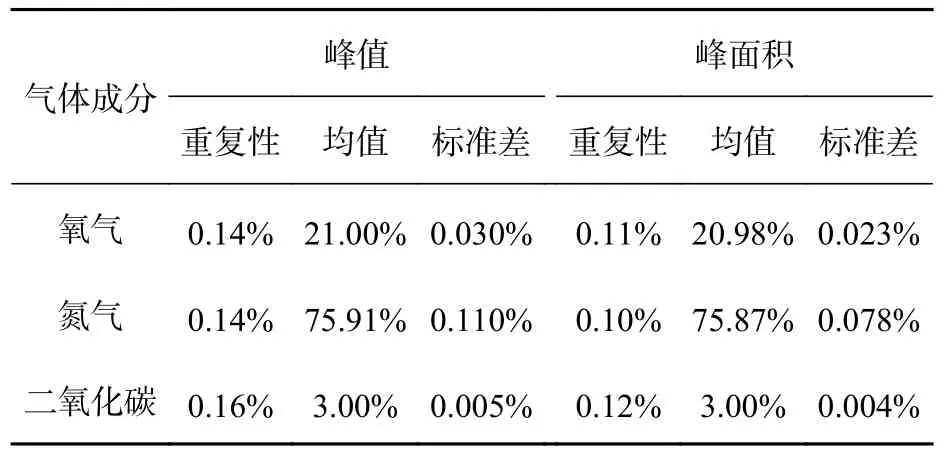
表2 瑞利散射归一化法计算结果Tab.2 Calculation results of Rayleigh scattering normalization method

通过对比表1 与表2 结果发现，采用瑞利散射归一化的方法相对于峰值、峰面积法可以提升测量的重复性与稳定性，降低激光器功率波动带来的影响，且不受所有气体体积分数和为100%的约束。由于瑞利散射比拉曼散射强很多，随着积分时间的增大，瑞利散射强度随积分时间的变化更快，导致比例失调。因此，采用瑞利散射归一化的方法无法运用到不同积分时间的情况下。

3.3 某一种气体成分归一化

某一种气体成分归一化在文献[3]中命名为混合物拉曼光谱线性叠加模型。计算过程参考文献[3]。

采用该方法对0.1 s 积分时间下的23 组数据进行定量计算。采用氮气作为归一化气体成分，计算结果见表3。

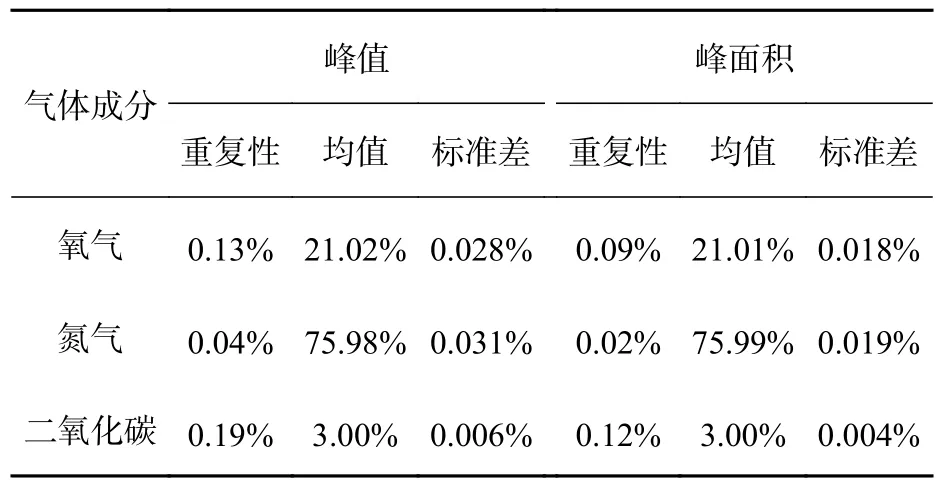
表3 氮气归一化法计算结果Tab.3 Calculation results of nitrogen normalization method

表3 与表2 对比，采用氮气归一化的方法，测量重复性与稳定性较高。但是，该方法要受到所有气体成分体积分数和为100%的约束。如果待测气体体积分数的和不为100%，该方法计算结果将会出现较大误差。为了进一步分析误差情况，采集以氩气为底气的体积分数均为1%的一氧化碳、二氧化碳、氧气、氮气、硫化氢、氢气6 种气体成分，14 组拉曼谱图数据，其中一组数据如图4 所示。图5分别为氧气、氮气和二氧化碳的14 组数据定量分析结果。图5 中，二氧化碳、氧气、氮气的体积分数计算结果达到33.3%左右，误差已达30%以上。

图4 1 s 积分时间30 次累加6 种气体的拉曼谱图Fig.4 Raman spectra of six gases accumulated 30 times at 1 s integration time

图5 不同气体的对应14 组数据定量的计算结果Fig.5 Calculation results of gases of 14 groups data

采用氮气归一化的方法也无法消除积分时间的影响。采用0.1 s 积分时间数据做定标，图6分别为氧气、氮气和二氧化碳对应12 组不同积分时间下的数据进行计算的结果。随着积分时间的变化，计算结果误差逐渐增大。

图6 不同气体在不同积分时间下的计算结果Fig.6 Calculation results of gases under different integration times

采用氮气归一化的方法是4 种方法中重复性与稳定性最高的方法。但是，受到待测气体成分体积分数和为100%的约束，同时也无法适用于不同积分时间的情况。

3.4 待测气体成分整体归一化

在采用峰值、峰面积法或者瑞利散射归一化得出气体体积分数之后，采用待测气体成分整体归一化的计算方法，即：

式中：ai为最终气体体积分数；ci、cm为采用峰值法、峰面积法或瑞利散射归一化得到的第i、m种气体体积分数。这里采用峰值法和峰面积法对0.1 s 积分时间的数据进行定量计算。计算结果见表4。

对比表4 与表1 数据，采用待测气体成分归一化方法相比峰值法、峰面积法可以提升测量重复性与稳定性。同时，可以避免积分时间的影响。采用0.1 s 积分时间的数据进行定标，对氧气、氮气和二氧化碳的12 组不同积分时间数据进行定量计算，结果如图7 所示。积分时间从0.1 s 到4 s，氧气、氮气、二氧化碳计算误差最大分别为：0.45%、0.65%、0.23%。采用瑞利散射归一化的方法可以进一步提升重复性、稳定性，针对不同积分时间数据可以进一步降低误差。

图7 不同气体在不同积分时间下的计算结果Fig.7 Calculation results of gases under different integration times

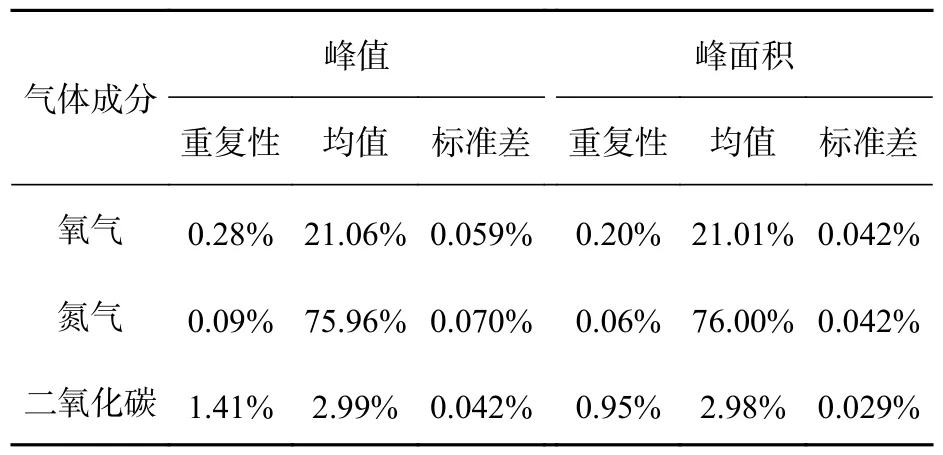
表4 待测气体成分整体归一化法计算结果Tab.4 Calculation results of the overall normalization method for the gas composition

采用待测气体成分整体归一化方法，可以避免积分时间的影响，但同样受所有气体成分体积分数和为100%的约束。

最后对4 种方法的优缺点进行了总结，见表5。

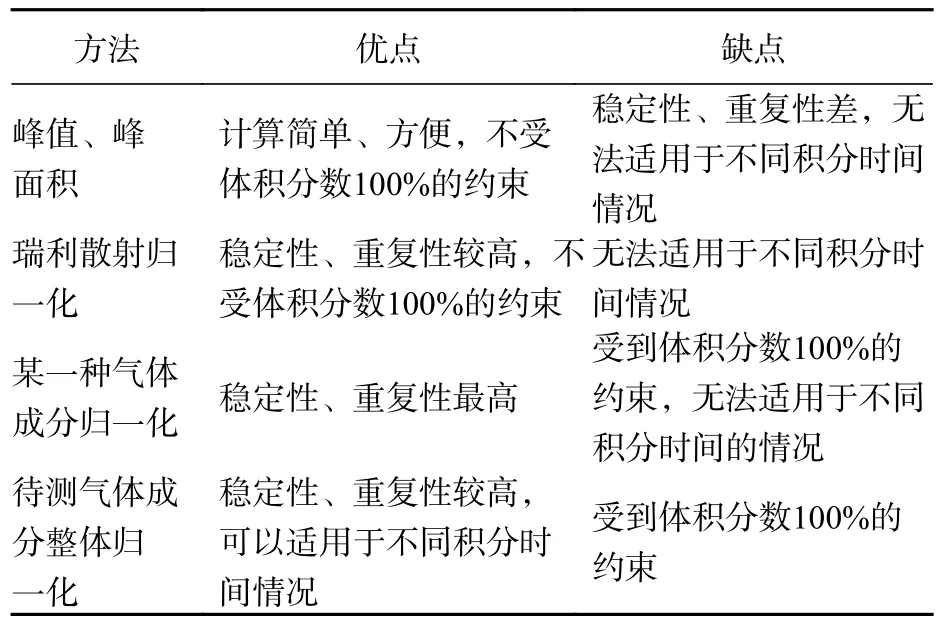
表5 4 种方法优缺点总结Tab.5 The advantages and disadvantages of the four methods

4 结论

在多组分气体拉曼光谱产品开发过程中，定量检测算法的开发是其中的关键内容。当待测气体成分体积分数跨度较大，需要使用不同的积分时间进行定量检测，那么就需要使得标定的结果适用于不同积分时间的情况，这种条件下可以采用待测气体成分整体归一化的方法。当待测气体成分体积分数和与100%相差较大，可以采用瑞利散射归一化的方法。当待测气体成分中存在一种含量较高的固定成分，例如文献[2]的甲烷，文献[7]中的水，可以采用对某一种成分归一化的方法，提升测量的重复性，稳定性。在产品开发过程中，开发人员需要根据具体的应用场景，选取合适的方法。