一种惯性交替极小化算法及其应用

吴双双，唐玉超

(南昌大学数学系，江西 南昌 330031)

1 引言与研究背景

在本文中，我们主要考虑以下形式的凸极小化问题：

(1)

其中H1和H2是实Hilbert空间，f:H1→(-∞,+∞]和g:H2→(-∞,+∞]是正则下半连续凸函数，G是实Hilbert空间，A:H1→G和B:H2→G是非零有界线性算子，以及b∈G。我们假设f是σ-强凸的，其中σ>0。下面，我们介绍几个信号和图像处理中的具体问题，可以看作是问题(1)的特例。

例1(全变分图像去噪问题)全变分图像去噪问题最早由Rudin、Osher和Fatemi[1]提出，其形式如下：

(2)

其中u∈Rm×n是观测到的噪声图像，‖x‖TV表示全变分，λ>0是正则参数。(2)通常被称为ROF模型。因为模型中的全变分‖x‖TV可以表示为凸函数φ和一阶差分算子L:Rm×n→Rm×m×Rm×n的组合，即‖x‖TV=φ(Lx)[2-3]。因此，(2)可以表示为下面的形式：

(3)

如果令y=Lx，则(3) 可以写成如下形式：

s.t.Lx-y=0

(4)

例2(具有约束的全变分图像去噪问题) 考虑到数字图像中像素值往往分布在[0,1]或[0,255]之间。设C是一个非空闭凸集，考虑如下具有约束的ROF模型[4-6]：

s.t.x∈C

(5)

通过使用示性函数δC(x)，以及‖x‖TV=φ(Lx)， (5)等价于：

(6)

s.t.Lx-y=0

(7)

这也是(1)的一个特例。除此之外，还有许多问题是(1)的特例，例如闭凸集交集上的投影问题[7-8]，强凸鲁棒主成分分析(RPCA)问题[9-10]和资源分配问题[11]等。

交替方向乘子法(ADMM)是求解(1)的一种常用方法，最早可以追溯到Gabay和Mercier[12]、Glowinski和Marroco[13]以及Gabay[14]等人的工作。众所周知，ADMM等价于Douglas-Rachford分裂算法[15]应用于(1)的对偶问题。为了充分利用(1)中f(x)的强凸性，基于邻近梯度算法(也称为向前向后分裂算法)，Tseng[16]提出了一种交替极小化算法(AMA)求解问题(1)的对偶问题，具体算法如下：

(8)

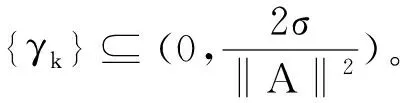
为了加速AMA(8)，Goldstein等[17]基于快速迭代收缩阈值算法 (FISTA)[18]提出了一种求解(1)的对偶问题的算法，即Fast AMA：

(9)

由于Fast AMA (9) 是由FISTA推导建立的，其步长参数范围比原始AMA (8)小，而文献[17]并没有证明序列{xk}和{yk}的收敛性。因此，本文的主要目的是提出一种用于求解(1)的惯性交替极小化算法，该算法源于惯性邻近梯度算法。我们不仅分析所提出算法的收敛性，而且证明所提出的算法收敛到原始问题(1)和对偶问题的最优解。作为应用，我们将所得算法用于求解一类复合凸极小化问题。为验证所提出算法的有效性和优越性，我们考虑具有约束的全变分图像去噪模型，该模型包含非空闭凸集约束和全变分正则项。

本文的主要贡献：(ⅰ)提出一种惯性的交替极小化算法求解凸极小化问题(1)，其中AMA(8)可以看作本文所提算法的特例。(ⅱ)证明所提出算法同时收敛到问题(1)和其对偶问题的最优解。(ⅲ)应用所提算法求解具有约束的全变分图像去噪模型，数值结果表明了所提算法的优越性。

本文具体安排如下：在第2节，我们回顾凸分析中的一些基本的定义和重要结论。在第3节，我们介绍所提算法并证明其收敛性。在第4节，我们利用提出的算法来解决一类复合凸优化问题。在第 5节，通过数值实验说明所提出算法的性能。最后，我们给出全文小结。

2 预备知识

C上的投影用PC表示，定义为PC(x)=argminy∈C‖x-y‖。

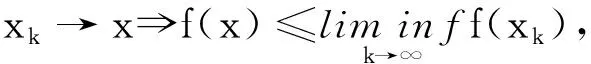
定义1[20]设f:H→(-∞,+∞]，

(ⅰ)如果

f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y),∀x,y∈domf,λ∈[0,1]

那么f是凸的。

f在x处的次微分定义为:

∂f(x)≡{v∈H|f(y)≥f(x)+〈v,y-x〉,∀y∈H}

注意f是凸的就意味着∂f是单调的，即

〈x-y,u-v〉≥0,∀x,y∈H,∀u∈∂f(x),∀v∈∂f(y)

此外，如果f是σ-强凸的，则∂f是σ-强单调的，即∂f-σI是单调的。

定义2[20]设f∈Γ0(H)，则f的Fenchel共轭定义为

由f∈Γ0(H)，可以得到(∂f)-1=∂f*。

定义3[20](邻近算子)设λ>0，f∈Γ0(H)，λf的邻近算子定义为：

如果f(x)=δC(x)，那么proxλδC(x)=PC(x)。

Moreau[21]首次提出了邻近算子的概念，它在设计和解决凸优化问题的邻近算法中起着非常重要的作用。下面的引理展示了如何利用一个正则下半连续凸函数f的凸共轭f*或其逆来计算它本身的邻近算子。

引理1[20](Moreau's decomposition)设λ>0，f∈Γ0(H)，则

定义4[20](Moreau envelope)设f∈Γ0(H)，λ>0，则Moreau envelope可以表示为：

下面的引理表明Moreau envelope在H上是可微的。

2.1 惯性邻近梯度算法

考虑下面凸极小化问题：

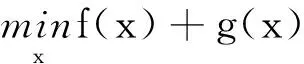
(10)

其中f:H→R是具有L-Lipschitz连续梯度的凸可微函数，L>0，g:H→(-∞,+∞]是一个正则的、下半连续凸函数。邻近梯度算法 (PGA) 是求解(10)的一种常用的方法。PGA 可以看作是在凸极小化问题中向前-向后分裂算法[22-24]的一种特殊情况。此外，惯性邻近梯度算法是一种有效的加速邻近梯度算法被广泛应用于求解问题(10)。下面，我们给出关于惯性邻近梯度算法的收敛性定理，具体证明可以参考文献[25]。

定理1设g∈Γ0(H)，f:H→R是具有L-Lipschitz连续梯度的凸可微函数，其中L>0。假设 argmin(f+g)≠∅，x0∈H，定义

(11)

如果{αk}和{γk}满足下列条件之一：

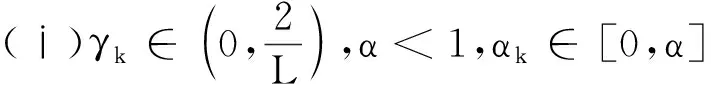
则以下结论成立：

(b){xk}弱收敛到argmin(f+g)的一个极小点。

2.2 最优性条件

对于前面我们所考虑的凸极小化问题(1)，它的拉格朗日函数定义为

L(x,y,p)=f(x)+g(y)+〈p,b-Ax-By〉

(12)

我们通过极小化关于x和y的拉格朗日函数(12)来获得对偶问题，如下所示：

(13)

其中f*和g*分别是f和g的Fenchel共轭。如果

L(x*,y*,p)≤L(x*,y*,p*)≤L(x,y,p*),∀(x,y,p)∈H×G×K

则称(x*,y*,p*)是拉格朗日函数L的鞍点。众所周知，当且仅当 (x*,y*)是(1)的最优解，p*是(13)的最优解时，(x*,y*,p*)是拉格朗日函数L的鞍点，并且原始问题(1) 的最优值和对偶问题(13)的最优值是相同的。(x*,y*,p*) 通常称为(1)和(13) 的原始-对偶最优解。

引理3[11](x*,y*,p*)是拉格朗日函数L的鞍点，当且仅当

A*p*∈∂f(x*)

B*p*∈∂g(y*)

A*x*+B*y*=b

(14)

最后，在本文中我们将充分利用以下余弦等式：

2〈a-b,c-a〉=‖b-c‖2-‖a-b‖2-‖a-c‖2,∀a,b,c∈H

(15)

3 惯性交替极小化算法收敛性分析

在本节中，我们提出一种用于求解(1)的惯性交替极小化算法，它可以看作是原始AMA算法(8)的推广。下面我们给出惯性交替极小化算法的具体格式。

算法1惯性的交替极小化算法

当αk=0时,所提出的IAMA退化成原始的AMA(8)。下面，我们证明所提的惯性交替极小化算法的收敛性。

定理2考虑问题(1)，假设拉格朗日函数(12)的鞍点集是非空的，{xk},{yk}和{pk} 是由算法1生成的序列，如果{αk}和{γk}满足下列条件之一：

(16)

(17)

则存在拉格朗日函数L的一组鞍点(x*,y*,p*)，使得：

(a)pk⇀p*；

(b)xk→x*；

(c)Byk→By*；此外，如果存在β>0，使得B*BβI，则yk→y*；

证明(a)由引理4可知，f*(A*p) 是连续可微的，并且具有Lipschitz连续梯度。在对偶问题(13)中，极小化的是一个光滑函数和一个凸函数的和，因此我们可以应用惯性邻近梯度算法来求解(13)，即：

(18)

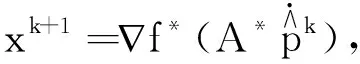
(19)

即

(20)

将h(p)代入(18)的第二个式子，有

(21)

由(21)可得到其一阶优化条件为

(22)

设yk+1∈∂g*(B*pk+1),我们有

0∈∂g(yk+1)-B*pk+1

(23)

以及

(24)

这是我们所提出算法的最后一步。由(23)和(24)，我们可以得到

(25)

这是惯性交替极小化算法的第三步。根据定理 1，我们可以得到pk⇀p*。

(b),(c)由一阶优化条件和算法可得到

(26)

和

(27)

根据∂f强单调和∂g单调，则有

(28)

和

(29)

将(28)和(29)相加，可以得到

(30)

根据pk+1的定义，以及Ax*+By*=b，可以得到

(31)

将(31)代入(30)，可以得到

(32)

对(32)利用余弦等式，我们有

(33)

接着在上述不等式两边乘以2γk，经过移项和整理可以得到

(34)

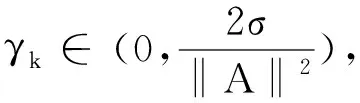
(35)

设φk=‖pk-p*‖2，上式可以重新改写为

(36)

将(36)重新整理，可以得到

(37)

将(34)再次进行移项，可以得到

(38)

对(38)两边同时进行求和，则

(39)

在(39)两边取极限，即当k→+∞时，我们能够得到

即

xk→x*,Byk→By*=b-Ax*

如果β>0，使得B*BβI，那么yk→y*。

(d)下面我们证明目标函数值f(xk+1)+g(yk+1)收敛于(1)的最优解。由(12)所定义的拉格朗日函数L我们可以得到：

L(xk+1,yk+1,p*)≥L(x*,y*,p*)

(40)

把它展开来，即：

f(xk+1)+g(yk+1)≥f(x*)+g(y*)+〈p*,Axk+1+Byk+1-b〉

(41)

(42)

由算法1的一阶优化条件我们可以得到

(43)

由次微分的定义，可以得到：

(44)

把上面两个式子相加得到f(x*)+g(y*)≥f(xk+1)+g(yk+1)+〈A*(pk+αk(pk-pk-1)),x*-xk+1〉+〈pk+1,By*-Byk+1〉

(45)

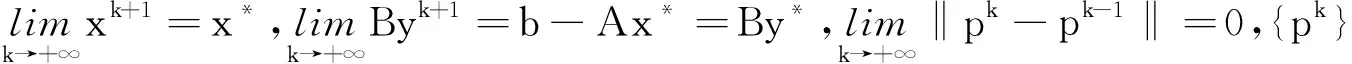
(46)

最后，结合(42)和(45)，可以得出

(47)

注1在定理 2中，我们证明了惯性交替极小化算法在两种条件下的收敛性。

(ⅱ)在第二种情况下，为了方便，我们固定步长参数γk，记为γ，根据文献[25]中的定理 2， (17)可以写为

因为序列{αk}是非递减的，所以0≤αk≤α(γ)，其中

α(γ)=1+

(48)

在本文中，我们取ε=10-6。

4 应用

在本节中，我们应用所提出的算法1来求解一类复合凸极小化问题，此类问题在信号和图像处理中具有广泛的应用。具体来说，我们考虑如下形式的凸极小化问题。

问题4.1假设g∈Γ0(H)、h∈Γ0(G)、b∈H，并且L:H→G是一个非零有界线性算子。考虑如下凸极小化问题：

(49)

我们对所考虑的凸极小化问题 4.1做以下假设：(i)，最优解存在；(ii)，满足一定的正则性条件，例如0∈sqri(L(domg)-domh)。 容易看出问题 4.1 是问题(1) 的一个特例。下面，我们给出具体的收敛性定理。

定理3在问题4.1的设定中，设p0∈G，定义

(50)

其中{γk}和{αk}满足定理2的条件。则下列说法成立:

(ⅰ){pk}弱收敛到(51)的对偶问题的一个最优解p*，其对偶问题为：

(51)

(ⅱ)x*=proxg(u+L*p*)是(51)的唯一最优解，并且{xk}强收敛到x*。

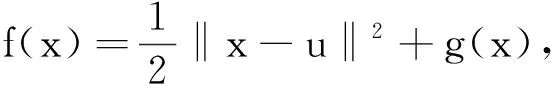
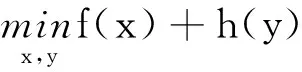
s.t.Lx-y=0

(52)

易见(52)是(1)的一种特殊情况。因此，我们可以应用算法1来求解(52)。从而我们得到如下迭代格式的算法：

(53)

由xk+1的一阶优化条件，可以得到

(54)

再由(53)中yk+1的定义和引理1，可以得到

yk+1=

(55)

将(55)代入到(53)的pk+1中，可以得到

(56)

即有(50)。

(ⅰ)根据定理2，我们知道{xk}强收敛到x*,{(yk,pk)} 弱收敛到 (y*,p*)，其中(x*,y*,p*) 是下面拉格朗日函数的鞍点：

L(x,y,p)=f(x)+h(y)+〈p,-Lx+y〉

(57)

由引理3，我们得到

(58)

根据(13)我们可以得到(52)的对偶问题是：

(59)

(ⅱ)由(58) 知，x*=proxg(u+L*p*)是(49)的唯一解，且{xk}强收敛到x*。

5 数值实验

在本节中，我们应用所提算法求解具有约束的全变分图像去噪模型(5)，并与其他算法进行比较。所有实验均在Windows 7和MATLAB R2016a下进行，该笔记本电脑的配置为 Intel Core i7-6700 CPU @3.40GHZ和8G RAM。在下文中，我们将具有约束的全变分图像去噪模型(5)称为C-L2-TV。通常存在两种类型的全变分：一种是各向同性全变分 (ITV)，另一种是各向异性全变分 (ATV)。它们都可以用凸函数φ和一阶差分算子L的组合来表示，即‖x‖TV=φ(Lx)。本文所提出的算法可应用于 ITV和 ATV。在下面的实验中，我们只使用ATV作为(5)中的正则函数，类似地可以处理ITV的情况。我们定义约束集合C={x|0≤x≤255}。

我们用峰值信噪比 (PSNR) 和结构相似性指数 (SSIM) [26]来衡量恢复图像的质量，其定义如下：

和

实验测试图像包括“Cameraman” 、 “Building”、“Boat”和“Goldhill”，如图1所示。

(a) 256×256 “Cameraman”图像(b) 493×517 “Building”图像 (c) 512×512 “Boat”图像 (d) 512×512 “Goldhill”图像

表1 不同图像在不同噪声水平下的最优正则参数选择Table 1 Optimal regularization parameter selection for different images under different noise levels

我们同时考虑了两种不同惯性参数条件下的IAMA，分别称为IAMA_1和IAMA_2。对原始图像分别添加均值为0和标准方差分别为σ=15,25和50的高斯噪声。为了获得最佳的去噪图像，我们调整了正则化参数，所得数值结果见表2。

在第一个实验中，我们比较本文提出的惯性AMA算法与原始的AMA算法在不同步长参数下的恢复效果。对于模型(5)，σ=1，‖L‖2=8，由注1，我们有

为了直观比较，我们给出α(γ)的图像，见图2。

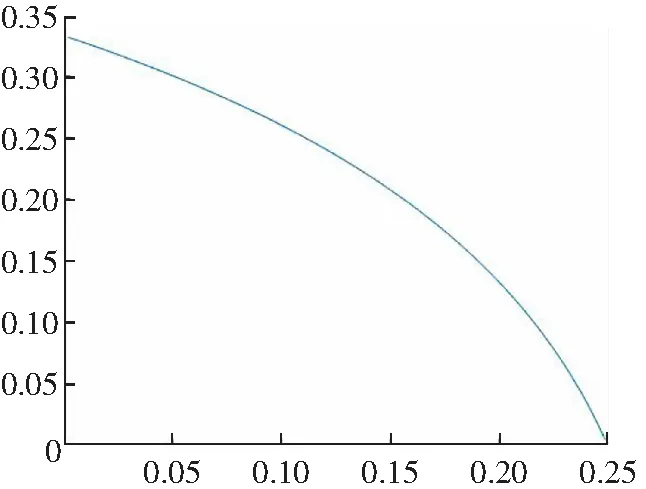
图2 由γ决定的惯性参数αk的上界Figure 2 The upper bound of the inertial parameter αk determined by γ

接下来我们设置了四种不同的步长参数来进行试验，γk分别选取：γk=0.1,γk=0.15,γk=0.2,γk=0.225。在IAMA_2中，根据注1我们取：αk=0.26,αk=0.207,αk=0.132,αk=0.078。这里的测试图像为“Building”，我们对原始图像添加均值为0 和标准方差为σ=50的高斯噪声。

所得数值结果如表2所示，由表中数据我们可以看出来，在不同的步长参数下，iAMA_1和原始的AMA在峰值信噪比 (PSNR)、结构相似性指数 (SSIM) 以及迭代步数的数值结果都是一致的。在给定停止条件下，随着γk在取值的增大，3种算法所需迭代次数逐渐减少。同时，IAMA_2算法比原始的AMA算法收敛稍快。

表2 惯性AMA和原始AMA在不同参数关于PSNR、SSIM 和 Iter的数值结果Table 2 Numerical results of the proposed inertial AMA and the AMA in terms of the PSNR,SSIM and Iter with different parameters

在第2个实验中，我们测试了惯性AMA和原始AMA在对于不同图像且在不同噪声下的恢复效果。我们统一设置γk=0.1。在IAMA_1中，我们按照注1对惯性参数来进行更新。在IAMA_2中，我们设定惯性参数αk=0.26。

表3展示了4幅图像在不同噪声水平下去噪效果的数值结果。由表中数据可以看出来，IAMA_1和原始的AMA所选取的图像在不同的噪声水平下的峰值信噪比(PSNR)、 结构相似性指数(SSIM)以及迭代步数 (Iter) 几乎都是一样的。对于所有的测试图像，在不同噪声水平下，IAMA_2的迭代步数都是要比原始的AMA迭代步数少。在4幅测试图像中，噪声水平比较大的时候，即σ=50时，IAMA_2的恢复效果都要比原始的AMA恢复效果稍好。在“Cameraman”图像中，对于设定的3种噪声水平，IAMA_2 的恢复效果都要比原始的AMA恢复效果稍好。总体来说，我们所提出的算法比原始的AMA算法具有一定的优越性。接下来，我们展示“Cameraman”图像在不同噪声水平下，本文所提算法与原始AMA算法的恢复效果，如图3所示。

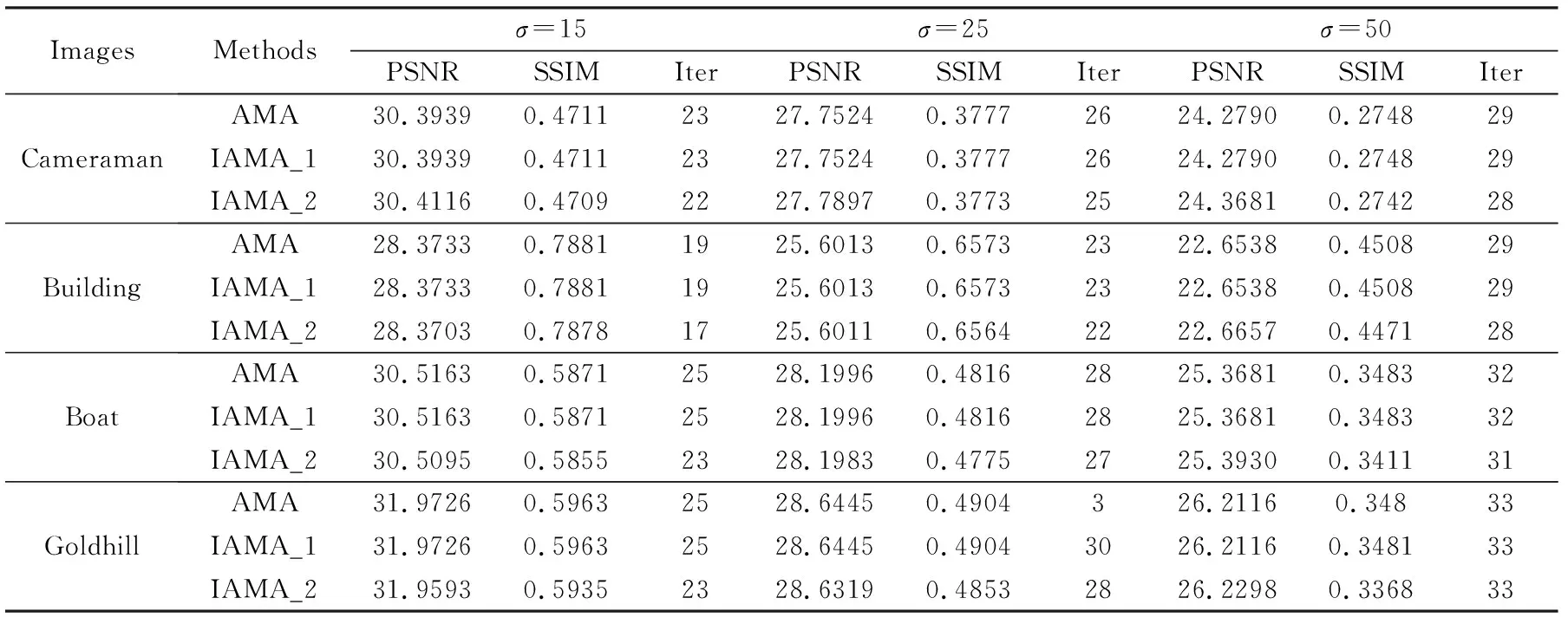
表3 所提算法在两种不同的惯性参数设置下与AMA的数值结果Table 3 Numerical results of the AMA and the proposed algorithm under two different inertial parameter

(a)σ=15 (b)σ=25 (c)σ=50

(d)AMA (e)AMA (f)AMA

(g)IAMA_1 (h)IAMA_1 (i)IAMA_1

(j)IAMA_2 (k)IAMA_2 (l)IAMA_2

6 结论

为解决具有线性等式约束的两块可分离凸极小化问题(1)，我们提出了一种惯性交替极小化算法，所提出的算法推广了 Tseng[16]提出的经典交替极小化算法。在实Hilbert空间中，我们证明了所提出的算法在两种不同惯性参数条件下的收敛性。进一步，我们应用所提出的算法求解一类复合凸极小化问题，该问题在图像处理，特别是图像去噪中具有广泛的应用。为了验证所提出算法的有效性和优越性，我们应用所提出的算法求解具有约束的全变分图像去噪模型。数值实验表明惯性交替极小化算法比原始交替极小化算法的迭代步数少。