慢读 细读 回读
——新高考数学阅读试题的教学思考
2022-11-18许家钊
许家钊
(苏州大学附属中学 215006)
1 数学阅读试题的教学现状
分析近年来的数学高考试题不难发现,情境试题明显增多,阅读量增大.这样设置的目的是让学生通过阅读提升数学学科素养,感悟数学思想方法,形成科学的数学思维,把握数学的本质.而现实情况是这一部分试题得分率较低,如2021年新高考Ⅱ卷的“卫星导航系统”、2021年新高考Ⅰ卷的“民间剪纸艺术”、2019年全国Ⅰ卷的“断臂维纳斯”等新情境试题让不少优秀学生折戟,主要有两方面的原因.
一是教师不重视.教师对数学阅读的理解不够深刻,没有形成数学也需要阅读的意识.课堂上,数学教师往往只注意逻辑推理的严密性、演算步骤的正确性、解题方法的恰当性,而忽略了引导学生理解数学语言,缺乏对数学语言的推敲琢磨.有些教师甚至认为,数学阅读费时费力,在提高学生成绩方面效果不明显,直接把数学阅读砍掉了.即便有部分教师认识到数学阅读的重要性,也只是停留在要求学生读读教材,以及对概念、公式和定理的圈圈画画上,这种阅读方式并不能提高学生的数学阅读理解能力.
二是学生不重视.学生潜意识里是轻视数学阅读的,他们眼中的阅读似乎只有语文、英语等学科才有,对于数学只要会做题就行了.对于布置的预习作业,很多学生一目十行,简单地过一遍,草草了事,既没有设定阅读任务,也没有设定完成的目标,只对教材中重要结论感兴趣,不能领悟其字里行间所蕴含的数学思想.
2 数学阅读试题的教学思考
笔者认为,数学阅读试题的教学可分为三个环节,即慢读、细读与回读.所谓慢读是指第一遍通读试题后,理解试题的大意,条件是什么、求什么、涉及数学课本里什么章节、可转化为什么样的数学问题,慢读可采用“一问一答”的方式进行,文章有举例说明;细读是指在慢读之后,在题中提取关键信息和所需数据,明确该数学问题的已知条件、所求问题需要哪些条件、采用什么计算方法、可否优化等;回读是指试题基本得到解决后,再回到试题当中,查看有无信息遗漏、有无隐含条件未使用、所求结果是否符合实际背景等.
例1(2021年新高考Ⅱ卷第4题)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为36 000 km(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O,半径r为6 400 km的球,其上点A的纬度是指OA与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为S=2πr2(1-cosα)(单位:km2),则S占地球表面积的百分比约为( ).
A.26% B.34% C.42% D.50%
慢读 问1:地球上一点A的维度是怎么定义的?试题表明是指线面所成角,是指直线OA与赤道平面的所成角,如图1,即∠AOB.问2:卫星的轨道高度是指什么?记卫星中心G与地球球心O的连线段与地球表面交于B点,那么轨道高度指的就是线段BG的长,如图2.问3:地球上能观测到卫星点的区域在哪里?过卫星点作地球表面的切线束,这些切点连起来形成一个小圆,这个小圆所包裹的地球表面都可以观测到卫星.问4:在这些观测点中维度最大的点在哪里?是小圆包裹的地球表面到赤道面距离最大的地方,如图3.

图1 图2

图3 图4

回读 卫星信号覆盖地球表面的表面积S=2πr2(1-cosα)是试题直接给出的,它与地球表面积的比值只与α有关,客观情况确实如此,卫星覆盖的地球表面可以类比成直线与圆相切所得的曲线段.
评注 本题涉及交叉学科,与地理学科相融合,解开神秘之面纱后,本质依然是数学中的基本问题,涉及直线与圆相切,直角三角形中的余弦以及球的表面积.借助于卫星导航系统的实际背景,考查学生数学阅读、绘图、转化、类比、降维等数学基本思想和方法的掌握情况,是一道优秀试题.
例2(2020课标全国Ⅱ卷第4题)如图5,北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层.上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块.下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块.已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( ).

图5
A.3 699块 B.3 474块
C.3 402块 D.3 339块
慢读 问1:场所被分为上、中、下三层,每一层的扇面形石板情况如何?上层的第一环是9块扇面形石板,第二环增加9块,是18块,这便形成了首项为9、公差为9的等差数列.问2:项数是多少?现在并不清楚,可以继续分析试题.问3:中层情况如何?也是等差数列.首项是多少?首项是上层最后一项再加上9块,说明上、中、下三层整个恰好构成了等差数列.问4:求什么?三层共有多少块石板,也就是求所有石板的总和,即求等差数列所有项的和,首项和公差都是9,现在只缺少项数.问5:题中还有什么条件?题中后段出现了重要条件“每层环数相同,下层比中层多729块”,使用好这个条件,便可以解决这个问题.
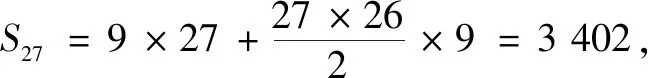
回读 本题实质是将等差数列27项等距离分成3段,每段9项,揭示的数学问题是比较容易的.
评注 本题以实际背景考查等差数列求和知识,所需的条件均蕴含于试题当中,需要考生通过阅读理解题意,提取重要数据,转化成数学问题,感悟数学与现实之间的关联.

慢读 问1:每一次对折有几种方式?两种方式,可以横向对折,也可以竖向对折,故第一次对折可以得到两种规格,学生有生活常识,容易理解.问2:试题已经告知对折两次,出现三种规格,为什么?因为将第一次横向对折之后的矩形再进行纵向对折,与将第一次竖向对折之后的矩形再横向对折所得图形相同,如图6,故而得到三种规格,这是一个非常重要的发现.问3:第三次对折结果如何?得到四种规格,如此,可知一般规律了.问4:对折4次可以得到几种规格?自然就是5了,解决了本题第一空的问题.

图6
细读 第1次对折,得到两种规格,分别是 6×20,12×10,所以S1=2×120;
第2次对折,得到三种规格,分别是3×20,6×10,12×5,所以S2=3×60;
第3次对折,得到四种规格,分别是1.5×20, 3×10,6×5,12×2.5,所以S3=4×30.
回读 每一次对折之后,每一种规格的面积都是原来的一半,规格的总数会增加一个,也就是说每次对折之后得到的所有规格总面积是一个等差数列乘以等比数列的形式,如此便恍然大悟,本题原来是用错位相减法.
评注 本题以生活常识为背景,考查对实际背景的阅读理解、绘图、运算求解以及转化等数学能力及应用意识,试题的本质是考查数列求和中的错位相减法.教学过程中,教师除加强引导阅读之外,对不熟悉的数列问题,还应引导学生先进行列举,逐步摸索规律,进而进行一般化处理,积累从具体到抽象的活动经验,体会从特殊到一般的数学思想方法.

A.8π B.6π C.9π D.5π


图7 图8
细读1 根据题目条件画出的图形,我们发现该图形有明显的对称性,故取BC中点O,连结AO,DO,如图8.此时,我们发现BC⊥平面AOD,所以平面AOD⊥平面BCD,因此,要作出A在平面BCD的射影,只需在平面AOD中作出OD的垂线即可.
主要解题过程1 如图9,取BC中点O,连结AO,DO,在平面AOD中,过A作AH⊥OD,交OD于点H.
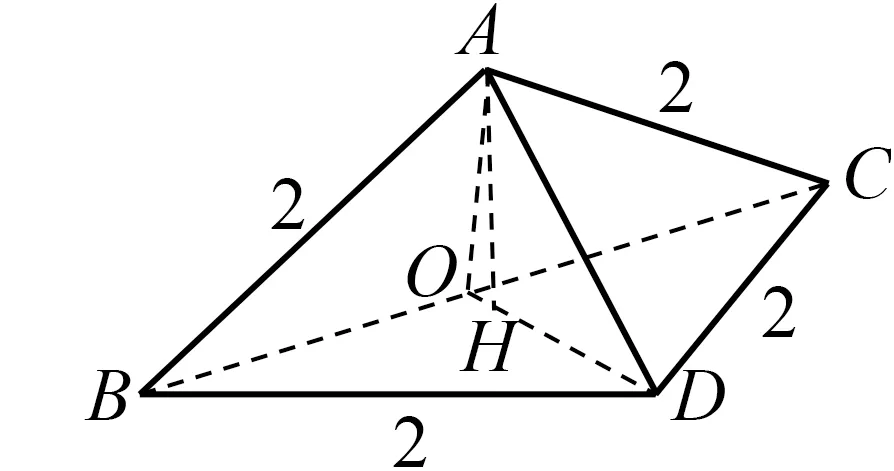
图9
因为O为BC中点,AB=AC,DB=DC,所以OD⊥BC,OA⊥BC, 又因为OD∩OA=O,OD,OA⊂平面AOD,所以BC⊥平面AOD, 又因为AH⊂平面AOD,所以AH⊥BC.


细读2 寻找几何体外接球球心的一般方法:确定几何体两个面的外接圆的圆心,并分别过这两个圆心作出垂直于这个面的垂线,两条垂线的交点即为球心.

回读 事实上,本题可以总结为一类特殊的模型——翻折模型,由一个等腰直角三角形绕着斜边旋转一定角度得到的三棱锥,其外接球球心位于斜边的中点.此外,翻折模型的题设往往会出现两个全

图10
评注 本题属于三棱锥的外接球问题,这类问题常见的模型有三种:模型一,有一条侧棱垂直于底面的三棱锥的外接球,通常是把它补成直三棱柱,利用勾股定理就可以轻松求解;模型二,正三棱锥的外接球,通常用两次勾股定理便可以搞定;模型三,一般三棱锥的外接球,通常需要找球心.而本题,由于两个侧面是等腰直角三角形,它的球心便是斜边中点,属于模型三的特殊情形.
3 结语
阅读作为数学基本素养之一,是学生获取信息和知识的重要途径,在高中数学的教学过程中,有计划地培养学生的阅读能力,有利于学生数学思维、逻辑分析能力的提升,可以促进学生综合能力的发展.教师重视对学生数学阅读能力的培养,不能简单地表现在增加情境题的数量上,关键要落实到课堂.教师应根据高考的要求、教材的特点、学生的实际,整合一些本源性、比较性、生成性资源,编写集知识性、方法性、趣味性于一体的阅读材料或情境性问题供学生阅读和思考,并以此创设阅读情境,提炼数学问题.每个学期,教师都应专门开设几节读题指导课,通过慢读、细读和回读,引导学生体会考点,引领本质的揭示、方法的迁移和模型的构建.
