格拉顿-吉尼斯的HPM思想*
2022-11-18徐伯华
徐伯华
(南通大学教育科学学院 226019)
朱凤琴
(南京信息工程大学无锡学院数理学院 214105)
艾弗·格拉顿-吉尼斯(Ivor Grattan-Guinness,1941—2014),英国米德尔塞克斯(Middlesex)大学数学史教授,一生致力于数学和数理逻辑的历史研究,2009年因“终身学术成就和贡献”与R.C.Gupta分享国际数学史学会凯尼斯·梅奖.在四十多年的职业生涯中,格拉顿-吉尼斯一直重视数学史的教育价值,不断思考数学史服务数学教育的问题,形成了独特的HPM思想.有评论说:他的思想随着时间的推移而逐渐成熟、逐渐拓展,虽具有一般主题上的统一性,但并不是铁板一块[1],主要是理论性的、指导性的[2].由于格拉顿-吉尼斯是一位专业的数学史家,并不专门研究HPM,有关HPM的论述散见于他的论文、评论、报告中,国内还没有系统的研究.本文运用文献研究法,以他的四篇文献[3-6]为主要研究对象,结合其他文献和评论,从思想基础、数学史的地位、解读数学史的方式、融入数学史的方法四个方面整理、概括他的HPM思想,希望给我国HPM
[2] 徐超.抛物线概念教学:重构数学史[J].教育研究与评论(中学教育教学),2015(8):26-31.
[3] 张佳丽.HPM视角下高中圆锥曲线的教学研究[D].南昌:江西师范大学,2018.
[4] 陆琳琰.抛物线的发生教学研究[D].上海:华东师范大学,2013.
[5] Tanner J H,Allen J.An elementary course in analytic geometry[M].New York:American Book Company,1898:67-68.
[6] Salmon G.A treatise on conic sections[M].Dublin:Hodges & Smith,1850:120-124.
[7] Smith P F,Gale A S.New analytic geometry[M].Boston:Ginn,1912:153.
[8] Ziwet A,Hedric E R,Hopkins L A.Analytic geometry and principles of algebra[M].New York:The Macmillan Company,1913:131.
[9] Roberts M M,Colpitts J T.Analytic geometry[M].New York:John Wiley & Sons,1918:110-119.
[10] Harding A M,Mullins G W.Analytic geometry[M].New York:The Macmillan Company,1926:120-124.
[11] Loomis E.Elements of analytical geometry and the differential and integral calculus[M].New York:Harper & Brothers,1851:44-53.
[12] Phillips H B.Analytic geometry[M].New York:John Wiley & Sons,1915:74-77.
[13] Bauer G N.The simpler elements of analytic geometry[M].Minneapolis,The H.W.Wilson Company,1903:38-41.
[14] Poor V C.Analytical geometry[M].New York:J.Wiley & Sons,1934:82-102.
[15] Reynolds J B,Weida F.Analytic geometry and the elements of calculus[M].New York:Prentice-Hall,1930:153-159.
[16] Biot J.An elementary treatise on analytical geometry[M].Philadelphia:Charles Desilver,1860:95-139.
[17] Loomis E.The elements of analytic geometry[M].New York:Harper & Brothers,1872:84-102.
[18] Smith P F,Gale A S.The elements of analytic geometry[M].Boston:Ginn & Company,1904:173-178.
[19] Hamilton H P.The principles of analytical geometry[M].Cambridge:J.Deighton & Sons,1826:142-143.
[20] Robinson H N.Conic sections and analytical geometry[M].New York:Ivison,Blakeman & Company,1860:50.
的理论和实践带来启发和帮助.
1 思想基础:数学知识并非凭空产生
格拉顿-吉尼斯之所以从事数学史研究,缘自他对数学教育的不满.早在20世纪60年代,他就感到数学教学多是按照整理好了的、严格的数学理论进行的,很少讨论问题的核心动机,甚至不讨论相关的历史发展与人的作用.四十多年后,他仍然说:“我的研究动机完全来自于对数学教育的消极反应……展现在我面前的是一系列令人赞叹的数学理论,但是为什么首先要研究这些理论?为什么教授方式差强人意?它们从哪里来的?没有人能在某个周四的下午坐下来,像教给我们的那样发明群论.”[7]
这种不满促使他思考数学的来源,思考数学史对数学教育的价值.他意识到,这些问题本身不是数学问题,而是数学哲学问题.于是,他向大名鼎鼎的波普尔(Karl Popper)求教,选修了硕士课程,攻读了博士学位,分别于1969年、1978年获得伦敦大学数学史哲学博士学位和科学史与科学哲学理学博士学位,从此走上数学史与逻辑史的研究道路.波普尔的科学观对格拉顿-吉尼斯影响很大,在梅奖发言中他还特别提到了以下几点:生命是一个问题解决的过程;科学总是处于猜想、验证、理论化的过程中;知识的生长比知识本身更重要;知识的基础是挖掘出来的,而不是建立其上的;认识不仅包括知的根源,还包括不知的根源;未来是开放的,既是主观的又是客观的.[7]
格拉顿-吉尼斯认为,数学知识不是凭空产生的,一个知识生长出另一个知识,有复杂而深刻的路径.对一个现代形式的数学知识,如果不了解它的发生动机、不了解它的发展过程,就不可能深刻地理解它.例如,作为数学基础的“集合”,看似简单,但要很好地理解它,绝非易事.康托既不是唯一、也不是首先研究集合的数学家,他的研究起源于黎曼的三角几何级数.在考察非收敛的“点集”与特殊级数间的关系时,他得出了两类非收敛点,由此定义了集合的类型,证明了连续统无限大于可数集,给出了超限算术的序数列,这是康托研究无限集的序、定义集合的势的真正起点.为了把有限算术和超限算术建立在一般的集合概念上,康托提出了朴素的集合定义,从而摆脱了序,建立了基数算术,并逐步使集合论成为测度论、分析学以及数学基础研究的有力工具.现在的教材只呈现加工好的、简化的集合理论,虽然让人容易接受,却不能让人领悟到它的优越性.
同样地,对一个现代形式的数学知识,如果没有相应的方法论支持,我们也不可能深刻地理解它.例如,很多人认为数学知识总是正确的,数学有可靠的基础,人们信任数学,就像信任欧几里得几何一样,这被称为欧几里得主义.随着现代数学的发展,数学的基础不在于定义是不是正确,而在于基本要素的一般性和简单性,数学重视的不再是不变的事实,而是不变的结构,人们对数学的可靠性、严谨性的认识发生了改变,这被称为新欧几里得主义.欧几里得主义、新欧几里得主义都不是数学知识本身,而是数学的方法论.方法论在数学体系中很重要,它决定着我们如何理解数学.例如,可误主义主张数学知识是在尝试中被接受的,其标准是能否成功地解决问题,除非一个技术性知识需要一个基础,否则就不存在基础知识.在这种观念下,数学知识就沿着技术和基础两个方向生长起来,表现出不同的层次和深度.要想很好地理解一个数学知识,就要熟悉它的基础性知识、技术性知识、方法论知识、认识论知识,这绝不是知识本身所显现的那么简单.
生长的观点、历史的观点能让我们看到数学知识的丰富性,从而更加深刻、更加准确地理解它.如果刻意简化数学,不仅会使知识肤浅化,还会让人难以理解,给人留下一个坏印象:数学就是用不平常的方式观察平常的事情.格拉顿-吉尼斯喜欢用“演进”(Convolution)解释数学的发展,而不是“革命”(Revolution).他认为,数学的发展从没有完全颠覆前期的成果,演进包括创新和替代,是一个认可、接受、拒绝、修正的动态过程,当谈到某个数学知识时,就不仅包含这个知识本身,还涉及与之相关的其他知识.例如:
(1)定义包含更多知识
数学定义并不是简单的命名方式,它所使用的判断和概念,要么是不明确的,要么是有定义的,要想很好地理解它,就要弄清楚这些判断和概念,以及凸显这些判断和概念之所以重要的那些语句.一些原创的定义为定理提供了证明,或者是公理的一种形式,其确切的意义只有通过重新解释定理或公理才能获得.
(2)数学理论有多个层次
对一般的数学知识来说,理性主义、经验主义是认识论知识,实证主义、可误主义是方法论知识.通常情况下,一般的数学知识包含于认识论知识之中,认识论知识又包含于方法论知识之中.数学理论就是由一般的数学知识、数学的认识论知识、数学的方法论知识构成的多层次的复杂体系.
(3)数学有三种表述
一是认识论表述,是由基本原理演绎出的形式系统,典型的是公理化系统.二是历史的表述,通过描述不同阶段的发展进程,如创造的发现过程、学术的影响过程等,历史地反映数学知识和数学理论.三是启发式表述,即从熟悉的情境中激发动机,获取实例,然后经过猜想、验证等一系列活动,最终在启发和思考中生成理论.认识论表述往往基于最新的观点去解释、梳理已有的知识.历史的表述则相反,往往挖掘更深的基础和背景,解释知识的由来.而启发式表述介于两者之间,既有认识论成分也有历史成分,在生成理论的同时,也带来更多的启发和思考.
2 数学史的地位:数学学习中的积极角色
数学知识不是凭空产生的,数学史在背后支撑着学生的学习和理解.你可以不关心数学史,不喜欢数学史,但不可能不受数学史的影响.在数学学习中,数学史是一个积极角色.与其讨论是否用数学史,还不如讨论如何自觉地运用数学史.数学史的积极角色具体表现为:
(1)模仿的对象
从某种意义上说,数学学习是数学研究的模仿.学生了解数学知识的早期发展,模仿数学的研究过程,不仅能获得知识,还能获得学习的途径和方法.模仿的对象有很多,如目标选择的背景、思路发现的途径,甚至曾经发生过的各种错误和策略.当然,模仿应该是启发式模仿,不能只是认识论模仿,因为认识论模仿更多地关心数学的结果,其价值是有限的.
(2)体验的素材
数学学习要获得知识,但更重要的是经历、体验一些创造性活动.如果学生面对数学史上的一个独创性问题,从不熟悉的情景开始,重构发明创造的过程,感受观念的萌生、发展和衰落,就会切实体会到数学的精神、思想和方法,看到数学活动中的“人”的真实世界.借鉴数学史,给学生一个真实的问题,虽然有可能增加学生的困难,但对学生的学习和发展是有深远意义的.
(3)研究的内容
数学大家对数学史往往情有独钟,他们认为如果一个观点很重要,那么其历史也就很重要,与之相关的因素就要仔细考察,然后才可能推进它.数学大家喜欢数学史不是被动的,他们知道要想做好数学,只能从历史中学习,没有别的办法.在数学学习中,数学史不是可有可无的陈词滥调,它应该成为数学学习的内在成分,通过研究前人的成就,了解更多的知识,激发创造的灵感,逐渐作出自己的贡献.
(4)学科理解的途径
形式化的数学有解无问、有答无疑,看不到“人”;编年体的数学能指出数学家的成就和局限,但常常以此评价后人;而实证主义能说明一个概念为什么重要,但彰显的是后来的观点,缺乏灵活性和广泛性.在数学学习中,上述方式都是需要的,把它们合在一起,才能体现出“人”的活动和价值.实际上,数学学习的内容不是那么重要,与之相联系的方法论更有价值.方法论可以解决不同的问题,越是自觉地使用它,越会得到更好的发展.数学史既包含数学的知识,又包含数学的方法论,既有科学性,又有人文性,对学生理解数学学科、感受数学文化、提高数学素养,都是至关重要的.
(5)启发动机的资源库
在知识和理解之间,数学史倾向于理解,通过提供动机、检验知识背后的发展和相互关系,帮助学生树立问题意识、调动研究兴趣、提高认识水平.成功的数学教育离不开深刻的、深入的思考动机,数学史上的问题、背景、应用、影响、不同层次的严谨、数学与其他学科的互动,都是启发动机的资源.甚至曾经发生的各种错误也是很好的动机资源.要知道,数学本来就是人类的一项活动,致力于解决有趣的问题,犯错在所难免,数学大家的一个错误往往比普通人做出的一百个无懈可击的小定理,更具有影响力和启发性.
3 解读数学史的方式:历史与遗产
对同一个数学史料,不同的人可能有不同的解读.例如,同样是读《原本》,史学家会发现,欧几里得处理的对象是线而不是长度,是平面区域而不是面积,而数学家则会融入方程的思想,从中读出几何代数来.格拉顿-吉尼斯认为,图形的解读和方程的解读都是合理的,没有对错之分,但却彼此不同,前者称为历史的解读方式,后者称为遗产的解读方式.
一般地,如果两个数学对象A,B有联系,并且A的出现早于B,就称A是B的历史;反之,称A是B的遗产.例如,方程对于欧几里得来说是遗产,对于笛卡尔来说是历史.
历史的解读方式,关注数学对象在特定时期的发展,包括它的前史、提出、早期形态、年表、内外影响与应用等,主要通过对过去的描述和解释来回答这样的问题:过去发生了什么?过去没发生什么?为什么会发生?为什么没有发生?数学史家常用历史的解读方式,希望在更广泛的意义上寻找数学活动的动机、根源、成果.
遗产的解读方式,关注数学对象对后期或者现在的影响,主要回答的问题是:我们是怎样来到这里的?给出的答案往往像一条康庄大道,似乎后期的成果早就蕴藏在前期的形态和观念之中了.实际上,这是对史料注入后期观念的结果.数学家常用遗产的解读方式,希望从过去的数学中获得现在需要的思想灵感.
通常情况下,一个数学对象既有自己的历史,也有自己的遗产.数学教育在历史资源和遗产资源的选择上,应该选择最能发挥教育效益的资源,而不是偏执一端.例如,在代数教学中,《原本》中的几何代数最能发挥效益,那就用它的遗产资源,或者说遗产地应用它;在几何教学中,线和面的几何最能发挥效益,那就用它的历史资源,或者说历史地应用它;而比例理论,既有助于几何教学,也有助于算术教学,那就根据教学的需要,既可以历史地应用它,也可以遗产地应用它.
格拉顿-吉尼斯对两种解读方式作了细致的区分.表1列出其中的一部分,这部分区分对教师解读具体的数学史料和资源选择可能有直接的帮助.

表1 历史方式与遗产方式的区别
4 融入数学史的方法:“历史-讽刺”教学法
格拉顿-吉尼斯认同历史发生原理,他说“教育模仿历史”,这样的例子比比皆是.例如零、分数、负数、未知数、常数、变量、方程、函数、极限、向量空间、线性代数、算术运算、超限算术等等.甚至对数学符号,也不能只讲授普遍使用的那一个,不同的符号有不同的历史,所有的符号都应该适当关注.
历史的或者发生学的方法,不仅能帮助学生深入地理解数学的动机、问题、概念及其联系,还能帮助教师清楚地表达、应对学生学习的困难,设计合理的教学活动.为了更好地发挥数学史的教学效益,格拉顿-吉尼斯提出以下教学策略:
(1)精选数学问题,围绕问题展开教学
问题的历史不一定显性呈现,但必须有足够的思考宽度,能广泛联系有关学科,让学生体会到问题的重要性.
(2)解释问题及其解答的重要阶段
说明每个阶段的发展贡献和外部因素,如果有可能,还可以指出该问题发展到现在的路径,或者指出现在还没有解决的有关问题.
(3)让学生在改造的历史情境中做出一些新结论
教学不必模仿繁琐的历史细节,可以给学生提供一定的知识基础或方法基础,让学生自己 寻找更多的细节和兴趣,或者从历史发展的某个中间环节开始,让学生自己探索解题的途径和目标.
(4)适当点拨方法论
通过方法论的提示和说明,让学生感受数学创造的不确定性、知识生长的双向性、数学理论的层次性,感悟数学的精神、思想和方法,体验“人”的活动和价值.
“历史-讽刺”法(history-satire),是格拉顿-吉尼斯根据自己的教学经验提出的一种独特的数学史融入教学的方法.在这里,“历史”指的是数学史资源,包括历史资源和遗产资源;“讽刺”指的是借助数学史资源激发学生的动机和思考,突出数学的意义,增强学生的数学理解.
该方法包括两个基本步骤:一是把历史文献翻译成当前的等价形式,便于学生理解原文、把握数学内容;二是把当前的教学内容嵌入到历史情境中,让学生在重构的历史情境中开展数学活动、实现教学目标.可以看出,该方法有明显的遗产倾向,第二步不可能完全符合历史的情景和进程,也不可能把当前教学的知识完全嵌入到历史情境中去,这是“历史-讽刺”法的特殊之处.
案例柯西闭线积分定理的教学.
柯西闭线积分定理:具有连续导数的单值可微函数在闭线C上的积分为0.很多学生对这个定理感觉奇怪,教材上利用柯西-黎曼方程和格林公式给出的快速证明更让学生一头雾水.
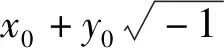
融入数学史的教学思路:实函数的积分定义早已讲过,学生比较熟悉.本定理的教学引入上述中间版本,能使学生在实分析的基础上更容易地理解该定理,这是一次“历史-讽刺”;而从中间版本到最后版本,能使学生在理解的基础上超越几何方式,更深刻地感受到分析的本质,这又是一次“历史-讽刺”.在两次讽刺中,教师还可以放大某些历史要素的意义,以便增强讽刺的效果.例如,把“几何的角色”作为一个问题提出来,让学生讨论,可以使学生更好地体会图形在分析中的地位和作用;把“柯西是否假设了f的导数是连续的”作为一个问题提出来,让学生思考,可以使学生更好地辨析残数定理的柯西版本与后来版本的不同.
“历史-讽刺”法的优点很突出,能够广泛地关注数学知识的历史资源和遗产资源,特别有益于当前教学的历史要素,既让历史服务于教学,又不让教学止步于历史、局限于历史.但是,缺点也很明显,一是讽刺的作用指向数学能力的培养,对基础概念的学习或者低年级的学习似乎不太合适;二是遗产的倾向容易导致历史失真,甚至历史曲解,让学生对数学学习尤其对数学研究产生偏见,从而不利于学生的长远发展.不过,这些缺点并非没法克服,只要教师善加应用,还是能很好地发挥数学史的积极作用的.
