综合体建筑弱电智能化工程设计

马 云

（烟台业达智慧城市运营科技有限公司，山东 烟台 265300）

1 工程概况

山东省烟台市某城市综合体开发项目位于城市东南角HD-2020-MCE2地块，设计为集城市商业、办公和居住的片区圈层，总建筑面积约115 380.95 m2，涉及居民住宅楼8栋，按E1～E8进行编号，其中E1栋、E3栋楼高为20层，其余楼栋楼高28层，层高均为3.0 m；公寓1栋，楼高为30层，每层5.5 m；商业办公楼（LOFT）1栋，楼高25层，每层3.2 m；商业裙楼2栋，涉及业态包括餐饮、娱乐、零售以及影院等。

2 建筑弱电布线目标函数的建立

建筑弱电布线问题可以认为是最优线路求解问题，通过建立以经济指标、功能指标、结构指标以及安全指标等目标函数，并按照一定的计算约束条件，进行求解。与一般的最优路线求解不同，建筑弱点布线约束条件具有专业特殊性，在建筑内的布线回路可以认为其起点是不确定的，而其重点都是固定的配电箱，弱电回路在建筑内的布置不能与墙体产生穿越交叉冲突，与窗口、其他管线预留孔洞等不能产生障碍，其敷设的路径也尽量紧贴墙面，在走廊和过道中则按照固定的排架和挂件进行布设，布设的线路也尽量保证平直无弯角，使施工更便捷[1-2]。

为此，研究建筑弱电布线的问题是可以将线路的总耗线长度S最小为目标函数，使所有的弱电回路的经济性目标达到最小[3]。假设建筑中分布有n个照明灯具pi，组成建筑中的照明灯具系列P={p1，p2，p3，……，pn}，任意2个灯具之间的距离l（pi，pi+1），可以用其空间坐标（xi，yi，zi），（xi+1，yi+1，zi+1），如公式（1）所示。

式中：l（pi，pi+1）为任意2个灯具之间的距离；xi，yi，zi为照明灯具pi的空间坐标；xi+1，yi+1，zi+1为照明灯具pi+1的空间坐标。

照明灯具系列的总耗线长度S如公式（2）所示。

式中：S为耗线长度；n为灯具数量。

在求解目标函数公式（2）时，弱点回路应服从的约束函数包括弯头总数w最少，任意取3个相邻灯具节点pi-1，pi，pi+1，中间灯具节点与前后2个灯具节点的夹角可以通过几何空间坐标进行求解，如公式（3）所示。

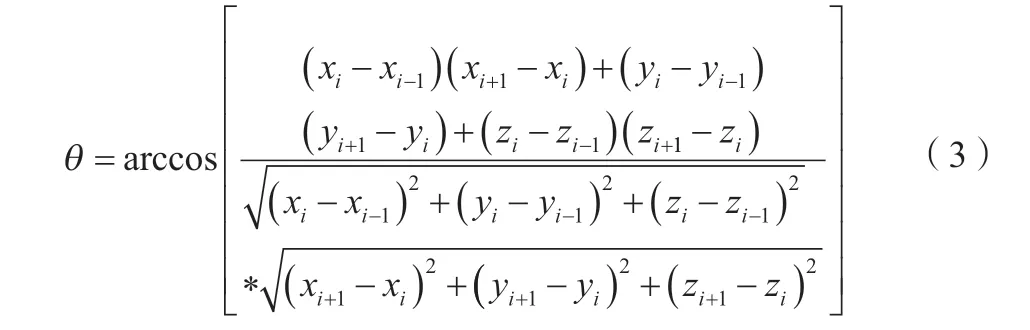
照明灯具系列的弯头总数w如公式（4）所示。

3 基于MATLAB软件的建筑弱电布线目标函数求解

3.1 建筑弱电布线三维模型的建立及目标函数的求解过程

基于上述目标函数，以项目中的商业办公楼（LOFT）为例，运用基于Auto CAD 图形编辑软件开发的VISUAL LISP工具建立楼层三维模型。VISUAL LISP工具中预留了程序接口，可以直接调用数学矩阵工具箱MATLAB程序，用于求解目标函数。MATLAB程序求解目标函数过程采用软件内嵌的混合粒子群算法计算包[3-4]，具体的计算流程如图1所示，在得到弱电线路的最优路径后，提取坐标信息并导入Auto CAD 图形编辑软件中，形成可视化的线路空间三维图像。

提取商业办公楼（LOFT）楼层中的房建几何尺寸信息，并统计房建中的照明用具熟练和插座数量，见表1。在Auto CAD 图形编辑软件中输入各个房间的坐标信息，生成平面图形，随后导入楼层的门窗尺寸和坐标信息，构建三维建筑模型。按照图1的流程设定混合粒子群算法（LWF）的计算种群规模为150，种群进化次数200次，并以同样的种群规模和种群进化次数分别采用常规遗传算法（GA）和改进遗传算法（OWF）进行结果对比，以分析3种计算方法的适应性。

表1 建筑三维模型参数

3.2 建筑弱电布线目标函数的求解结果分析

采用混合粒子群算法（LWF）、常规遗传算法（GA）和改进遗传算法（OWF）3种不同方法分别求解目标函数的算法训练过程，如图2所示。从图2（a）中可以看出，在照明用具的算法训练中，3种算法的训练过程中，适应度值均在初始阶段迅速下降，以较快的速度趋于稳定收敛。采用改进遗传算法（OWF）以最少的迭代次数（约10次）次得到最优适应度，但该方法得到的结果并非是全局最优，陷入了局部最优解的困局且无法逃逸，采用常规遗传算法（GA）在迭代30次后得到最优适应度，与混合粒子群算法（LWF）和改进遗传算法（OWF）相比，都需要较大的迭代次数，相对来说，混合粒子群算法（LWF）迭代次数较少（约15次），得到全局最优。

从图2（b）中可知，在插座的算法训练中，3种算法的训练过程中，适应度值均在初始阶段迅速下降，以较快的速度趋于稳定收敛，且改进遗传算法（OWF）、混合粒子群算法（LWF）的适应度值下降速率明显比常规遗传算法（GA）的适应度值快。采用常规遗传算法（GA）在迭代21次后得到最优适应度，但是该方法得到的结果不是全局最优，陷入了局部最优解的困局，采用改进遗传算法（OWF）、混合粒子群算法（LWF）可以在相同的迭代次数（约3次）得到全局最优。

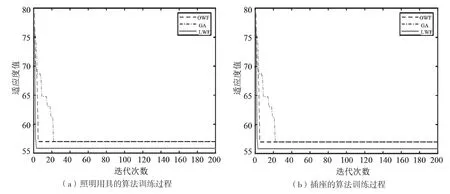
图2 不同计算方法的目标函数算法训练计算过程

图3为采用混合粒子群算法（LWF）、常规遗传算法（GA）和改进遗传算法（OWF）3种不同方法得到的办公室BGS1弱电回路对比。从图中可以看出，3种方法得到的照明用具回路、插座回路均没有出现交叉重叠、线路冗余的现象，说明3种方法都可以应用于建筑弱电线路的智能化布设。通过办公室BGS1插座回路路径的求解可知，其都可以得到最优线路，计算得到的总弯角为6个，而在办公室BGS1照明用具回路路径的求解中，3种方法得到的最优路径结果不同，改进遗传算法（OWF）得到的弯折点8个，常规遗传算法（GA）得到的弯折点9个，混合粒子群算法（LWF）得到的弯折点最少，弯折点数为4个，表明采用混合粒子群算法（LWF）可以得到最优的照明用具回路路径，其迭代步骤也存在优势，应用其在建筑弱点布线中具有明显优势。

图3 不同计算方法得到的BGS1弱电回路

以照明系统为例，对建筑楼层内所有房间的照明用具弱电线路进行计算，可以得到最终的计算结果如图4所示。从图中可以看出，所有房间的弱电线路直观立体、布线效果符合设计和规范的要求，弱电线路满足总耗线量最小的要求，符合线路排布的约束条件，且美观整齐，易于施工。所确定的计算方法符合智能化的工程设计要求，减少人工劳动力，为复杂综合体建筑弱电智能化工程设计提供了良好的算法。

图4 建筑楼层内所有房间的照明系统线路布局结果

4 结论

该文以山东省烟台市某城市综合体开发项目弱电线路布设为研究对象，建立总耗线长度的目标函数，通过基于Auto CAD图形编辑软件开发的VISUAL LISP工具建立楼层三维模型，采用混合粒子群算法计算最优线路路径，并与常规遗传算法和改进遗传算法计算结果进行对比，得到以下3个结论：1）在照明用具弱电路径和插座弱电路径的算法训练中，3种算法的适应度值均在初始阶段迅速下降，以较快的速度趋于稳定收敛。2）与其他2种方法相比，混合粒子群算法可以在较少的迭代步骤下可以得到全局最优路径，应用其在建筑弱点布线中具有明显优势。3）该文所确定的计算方法对所有房间的弱电线路进行排布，结果表明排布线路直观立体、布线效果符合设计和规范的要求，弱电线路满足总耗线量最小的要求，所确定的计算方法符合智能化的工程设计要求，减少人工劳动力。