从直观性角度对一道数列综合题的探究
2022-11-18200234上海师范大学数理学院
200234 上海师范大学数理学院 邓 聪
直观想象是《普通高中数学课程标准(2017年版)》提出的六大核心素养之一,它是指借助几何直观和空间想象来感知事物的形态与变化,利用空间形式特别是图形理解和解决数学问题的素养.数列问题是近年来高考数学的考查重点,内容较为抽象、复杂.
笔者针对2021年上海春考数学卷中的一道数列综合题进行探究,从直观性角度来解决该问题.数列可以视作是定义在正整数集上的特殊函数,因此具备函数的一些固有特征,而原题中的数列是一个具有随机性的数列.所以笔者将其视作特殊的分段函数,利用直观性观察函数的图像,从而研究数列的性质.巧妙地借助几何直观描述问题间的复杂关系,能使复杂问题简单化,抽象问题具体化,解题思路更加明朗.
1 解题探究
1.1 原题呈现
(2021上海春考数学卷-21) 已知数列{an}满足an≥0,对任意n≥2,an和an+1中存在一项使其为另一项与an-1的等差中项.
(1)已知a1=5,a2=3,a4=2,求a3的所有可能的取值.
(2)已知a1=a4=a7=0,a2,a5,a8为正数,求证:a2,a5,a8成等比数列,并求出公比q.
(3)已知数列中恰好有三项为0,即ar=as=at=0,2 图1 图2 图3图4 综上,a3的所有可能取值为1. 解:因为a1=a4=a7=0,且a2,a5,a8为正数,所以数列图像从a1处上升后必然要下降才能使得a4=0,又因为相连三项间的图像趋势满足图1或图2,所以图像在到达a2后就必须向下降落至零点,若上升到a3时才下降则此时图像不满足题意,同理可作出a4到a8的图像(如图5所示). 图5 当m=0时,即An的所有取值均为1,an+1=an+1,此时数列图像如图6所示. 图6 显然此时数列为等差数列且公差大于0,图像呈直线上升趋势,无法满足题干所述的恰有三项为0,所以m=0舍去. 图7 图8 小问(3)的难点在于求an+1,笔者在此过程中计算an+1-an,这是因为题干中的数列是一个随机数列,故可将其视作是一个分段函数,通过作差发现数列各项之间的关系,同时作出此时的图像,更加直观地帮助理解.小问(3)实则是小问(2)的拓展与延伸,在小问(3)中也得到了ar+1,as+1,at+1成等比数列,两小问都可以巧妙地利用好“拐点”个数,作出图像快速解题. 第一,本题研究的数列是一个随机数列,且该数列图像存在两种情况,单纯用代数方法解题十分复杂,因此笔者通过作图,建立起形与数的联系,通过几何图形描述问题,从直观性角度帮助理解问题. 图9 a3=a2+A2, a4=a3+A2A3, … (感谢冯朝君老师提供的部分思路)1.2 题干分析

1.3 解答
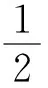




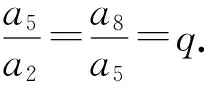




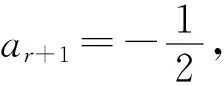
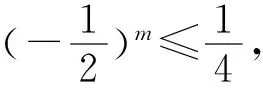




1.4 注记
2 拓展



