基于混沌序列的电力系统短期负荷预测
2022-11-17傅兴吉申艳伟尹照洪罗冲
傅兴吉,申艳伟,尹照洪,罗冲
(云南电网有限责任公司昆明供电局,云南 昆明 650000)
0 前言
对电力负荷进行准确预测关乎国家的稳步发展和人民的幸福生活。本文以混沌理论和混沌预测方法等方面的内容作为主要的架构进行分析和研究,希望找到适应性和可靠性较好的短期负荷预测算法,从而获得更好的预测精度和稳定性,为制定电力计划提供可靠的基础数据。混沌主要是指存在于确定性系统中的无规则运动,只有具备相关特点的非线性系统才能产生混沌。利用混沌理论进行预测的主要思路就是将时间序列嵌入到重构的相空间中,从而让新的状态轨迹保留这原来的主要特征。利用混沌理论进行预测,只需要通过相空间重构就可以近似恢复原来的多维非线性混沌系统[1],避免了其它多种繁琐预测模型的建立,也不需要了解各种负荷与相应影响因素之间的任何关系。混沌理论预测一般包含时间序列混沌特性的判别、确定延迟时间与嵌入维数、重构相空间和预测4 个基本流程。
本文利用混沌相关理论对短期负荷进行预测,其主要思想结合历史日负荷数据的混沌特性建立预测模型。大体思路如下:在获取到一系列实际历史负荷数据,并完成对负荷数据的处理后,对历史负荷数据序列内部相关参数进行求解,从而完成混沌特性识别,同时根据求得的相关参数数据对相空间进行重构,最后,建立基于最大Lyapunov 指数预测模型,实现负荷预测。
1 混沌时间序列及相空间重构概念
1.1 混沌时间序列
时间序列是对连续时间信号进行采样后得到的离散结果,混沌时间序列是一种特别的时间序列,它是由混沌的模型所产生的,具有与混沌一样的类似随机性,其动力学系统通常由系数确定的各类方程来描述。对于一个系统,我们必须对其是否混沌进行判断。
系统中任何一个变量的时间演化都包含了它的其他变量长期演化的信息,因此,我们分析系统的混沌行为时可以将该单变量时间序列作为基础。系统混沌时间序列中常用的几个特征量及其对应的表征作用如下:关联维反映了系统的复杂程度,Kolmogorov 熵反映了系统的混沌水平,Lyapunov 指数是系统混沌与否的关键,结合该指数的约束条件可以确定运动各阶段的相关特性。
1.2 相空间重构理论
一个系统在某一时刻的状态称为相,决定状态的状态变量构成的几何空间,称为相空间[2]。系统中任意一个分量的演化都是由与之相互作用的其它分量所决定的,因此这些相关其它分量的信息就隐含在该任一分量的发展过程中[3]。只要将这一个分量在某些固定的时间延迟点上的测量作为新维处理,以之确定某个多维状态空间中的一点,从而重构等价的状态空间。经过不断重复上述过程并测量各延迟时间的一个观察量,经过正确的处理过程,就可以重构出原动力系统的模型。如下从数学上对Takens 定理进行介绍:
定义1:设(N,ρ),(N1,ρ1)是两个度量空间,如果存在映射φ:N→N1满足:
1)φ满射;
2)ρ(x,y)=ρ1(φ(x),φ(y))(Ax,y∈N),则称(N,ρ),(N1,ρ1)是等距同构的。
定义2:如果(N1,ρ1)与另一度量空间(N2,ρ2)的子空间(N0,ρ2)是等距同构的,则称(N1,ρ1)可以嵌入(N2,ρ2)。
Takens 定理:M是d维流形,φ:M→M,φ是一个光滑的微分同胚,y:M→R,y有二阶连续导数,φ(x,y):M→R2d+1,其φ(x,y)=(y(x),y(φ(x)),y(φ2(x)),…,y(φ2d(x)),则φ(x,y)是M到R2d+1的一个嵌入。
按照Takens 定理就可以在拓扑等价意义下,对于某一个实测负荷数据时间序列{x(t),t=1,2,3,…,n},根据选取的相关参量,就可以将时间序列对象拓展成如下m维相量:
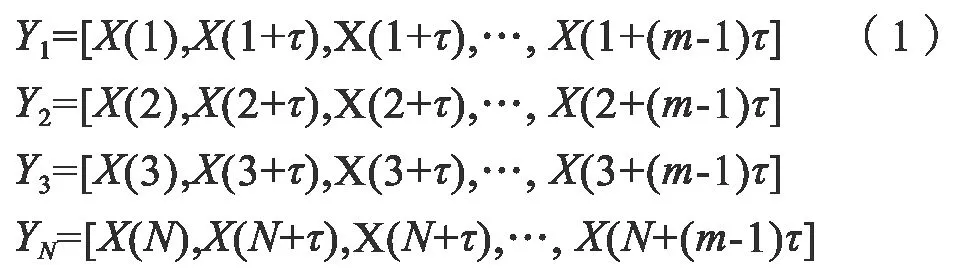
上式即为重构的相空间。其中,应当保证m≥2d+1,因为当嵌入维m<2d+1 时,相空间就不能恢复原有性质;而当嵌入维数取值过大时,高维重构相空间将会包含过多的冗余信息,因此当嵌入维大于某个最大值时,预测精度会随着嵌入维的增大而单调下降。而对于延迟时间的选取,当取值过小时,由于内部存在的一些原因将会使得信息不易显露;当取值过大时,由于蝴蝶效应的影响,重构的相空间不能很好地反映整个系统的特性。相关基本参数延迟时间τ与嵌入维m的选取在重构相空间过程中非常重要,过大或过小都会使重构的相位空间无法显示原始加载序列的动态。
2 短期电力负荷时间序列分析
2.1 整点负荷时间序列数据及预处理
本文获取了某市电网20 个小时的整点电力系统负荷数据,序列长度为1460 个小时,如图1 为该序列关于时间的二维曲线。本文用前1440 个整点负荷数据对后20 个整点负荷数据进行了预测。由获取到的负荷时间序列可知在这1460 小时内,最大负荷为4953 MW,最小负荷为2828 MW。
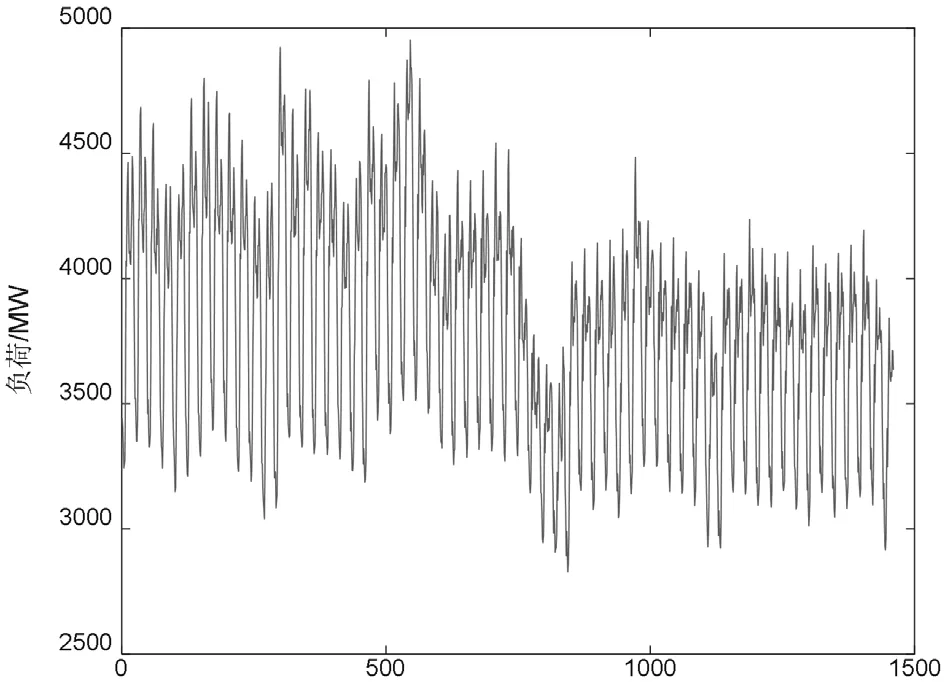
图1 某市负荷时间序列曲线
在负荷预测中,数据的可靠性和易处理性是预测工作顺利进行的关键,采用归一化方法对获取到的负荷时间序列数据进行预处理。
归一化处理用到的公式如下:
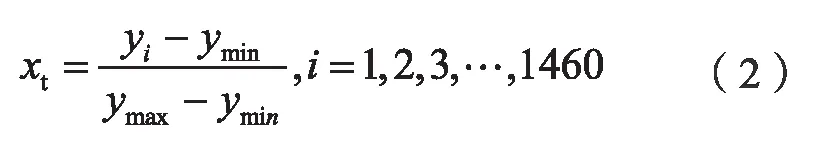
其中,通过查阅实际数据资料可知ymin=2828,ymax=4953,xt为负荷数据归一化后的数据时间序列。对获取到的数据进行归一化处理后,得到的负荷时间二维图形如图2 所示:
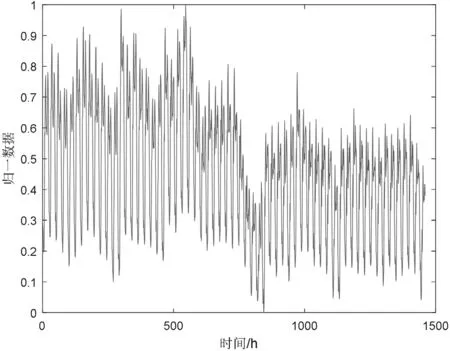
图2 预处理后的序列曲线
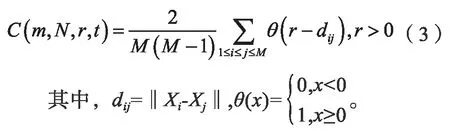
2.2 相空间延迟时间和嵌入维数选取
本文中,采用C-C 算法求延迟时间与嵌入维数:
设Xi=(xi,xi+τ,…,xi+(m-1)τ),Xi+∈Rm为重构的相空间,其中Xi(i=1,2,…,M)是重构相空间中的点,M=N-(m-1)τ,N为序列长度,m是嵌入维数,τ=t为延迟时间。定义该序列的关联积分为[4]:
由于C-C 算法的研究与函数S(m,N,r,t)=C(m,N,r,t)-Cm(1,N,r,t)的值有关[5]。为了找到合适的延迟时间及更好的研究时间序列的动力学特性,需要先把整个时间序列分为t个子序列。如果t=1 时,为单个时间序列本身,而t=2 时为{x1,x3,…,xN-1}及{x2,x4,…,xN},长度为N/2。对于一般的自然数有:
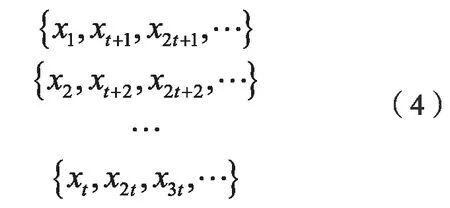
其中,N=tl,l=N/t是长度。对其它序列,将其分成t个不相交的子序列,然后将每个子序列的S(m,N,r,t)定义为:
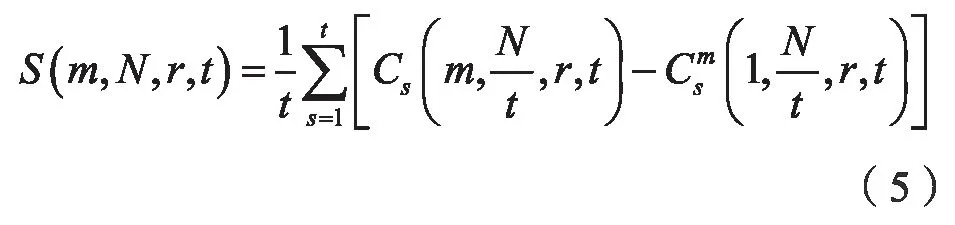
令N→∞,则有:
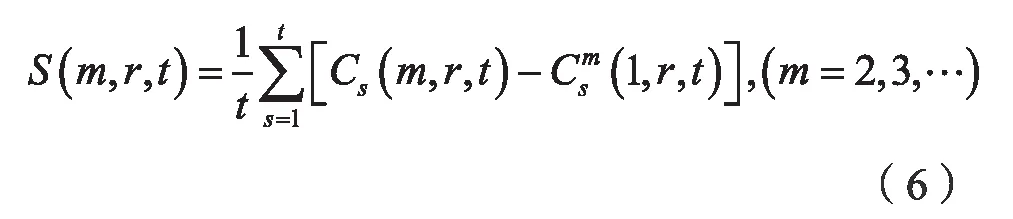
当N→∞时,对于所有的r,均有S(m,r,t)恒等于零。但实际的S(m,r,t)一般不等于零。这样,局部最大时间间隔就可以取S(m,r,t)的零点或对所有的半径r相互差别最小的时间点,因为这暗含着这些点几乎是均匀分布的[6]。选择对应值最大和最小半径r,定义其差量为:
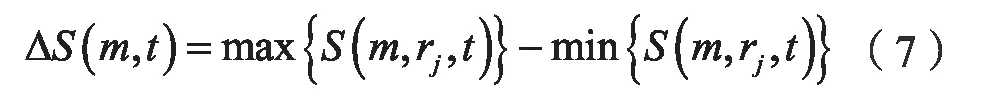
上式表示的是半径的最大偏差。根据相关的统计结论,取m=2~5,ri=,i=1~4,通过计算以下3 式:

上式中,将s(t)的第一个零点对应的时间选为延迟时间τ,同时将s_cor 在时间区间中的最小值对应的时间作为时间序列的第一个整体最大时间窗口tw,然后就可以根据延迟时间与最大时间窗口的关系式tw=(m-1)*τ,从而确定嵌入维数m。
根据上述C-C 算法思想,用MATLAB 编程软件进行编程调试,并将获取到的负荷时间序列写入程序中,运行C-C 算法程序后,得到的最大延时max_d与s(t)、delt_s、s_cor 三者之间的关系波形图如图3 所示。
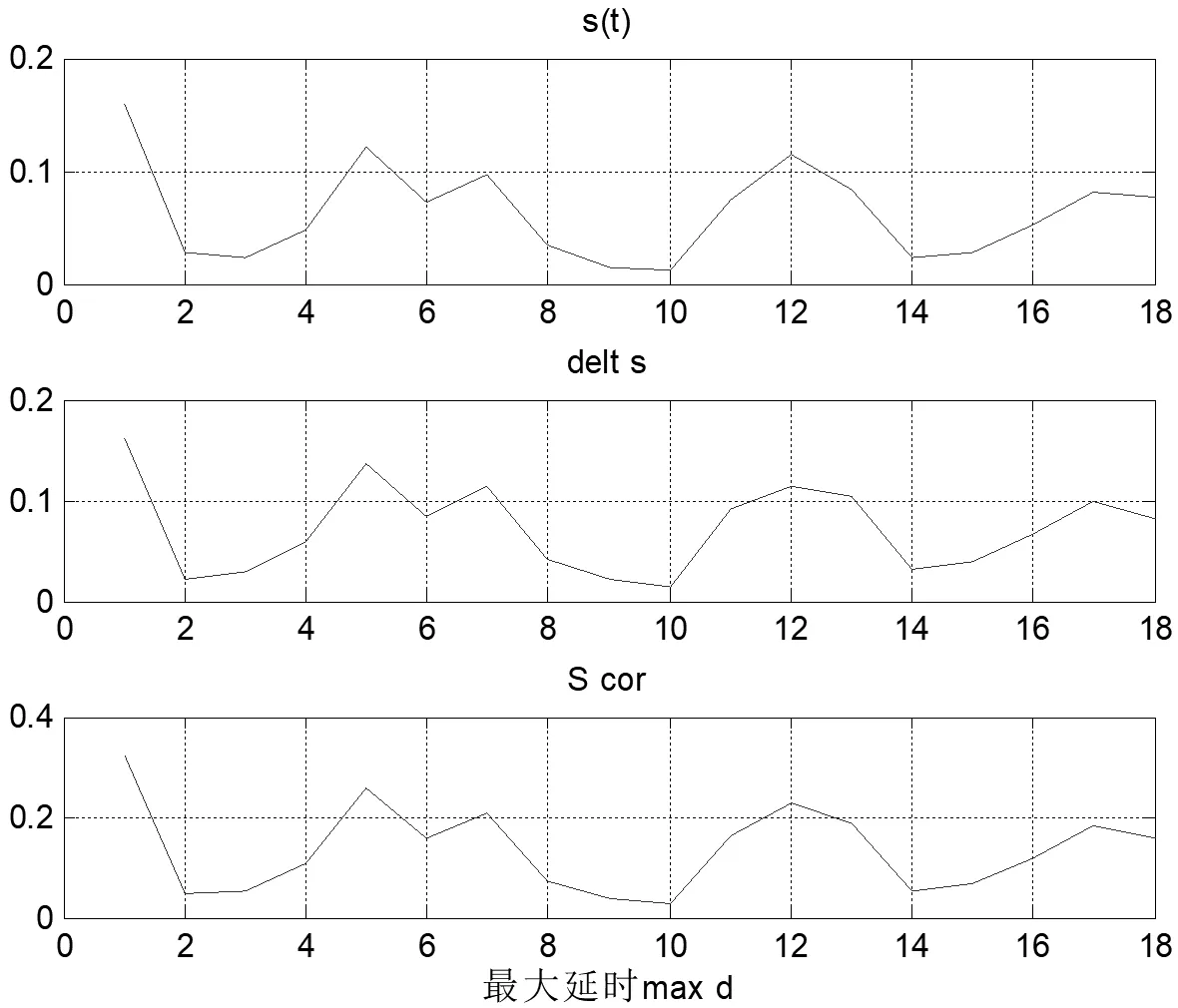
图3 C-C算法的输出图形
程序中最大延时max_d在1~18 之间取值。由图可知s(t)的第一个零点对应的时间为3,因此将其选为延迟时间即τ=3,在相应时间区间内s_cor 取最小值时对应的时间为10 因此将其选为延时时间窗口即tw=10,延迟时间和最大时间窗口都确定以后,根据公式tw=(m-1)*τ,可以求得重构相空间的嵌入维数即得m=4.33,据相关资料显示,重构相空间的最小嵌入维数一般向下取整,所以此处所取的嵌入维数为m=4。
2.3 最大Lyapunov指数
最大Lyapunov 指数不但是判断系统混沌与否的重要条件,而且它还是确定可预测时长的关键参数。采用小数据量法,求解实测负荷数据序列的最大Lyapunov 指数。
假设混沌时间序列为x1,x2,…,xn,其他相关参数的符号表示方法与前面相同,则重构相空间可得到Y(ti)={x(ti),x(ti+τ),…,x(ti+(m-1)τ)}(i=1,2,…,N),利用小数据量法计算最大Lyapunov 指数的具体思想如下:
1)利用C-C 算法同时算出嵌入维数m 和延迟时间τ。
2)根据实际所求得的重构参数,进行相空间重构后得{Yi|i=1,2,…,M}。
3)找到相空间中的每个点Yj和Yj,并进行限制短暂分离[15],即:

P为时间序列的平均周期[13],本课题中我们获取到的负荷时间序列,采用FFT 变换求得P=6。
4)对相空间中的每个点Yj,计算出该邻点对的i个离散时间步后的距离dj(i)。

5)对每个i,求出所有j的lndj(i)平均y(i),即:
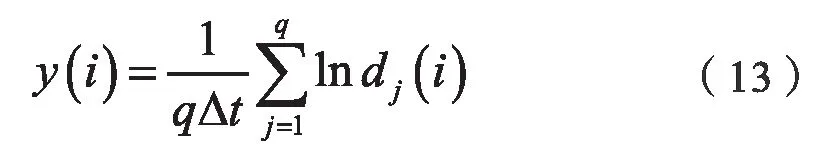
其中,q是非零dj(i)的数目,利用相关数学处理工具画出其回归直线,做出的回归直线的斜率,小数据量法示意图见图4。
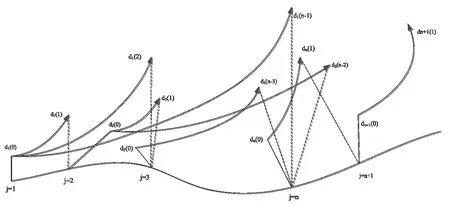
图4 小数据量法示意图
将2.2 中求得的相关参数τ=3、m=4,以及求得的时间序列的平均周期P=6 带入到程序中,运行wolf 程序后,求得λ1=0.0506。由此,可以确定该负荷时间序列为混沌时间序列,同时可以确定最大可预测时间长度Tmax=1/λ1=19.763。
3 基于最大Lyapunov指数的预测模型构建
基于最大Lyapunov 指数建立模型的基本思想如下:对一维的混沌时间序列进行相空间重构后,设预测的中心点为XM,设Xk为XM在其相空间中的最邻近点,二者的距离为dM(0),其最大Lyapunov 指数为λ1,则:

限制短暂分离,要求|M-j|>P,其中P混沌时间序列的平均周期。结合如下最大Lyapunov 指数的定义
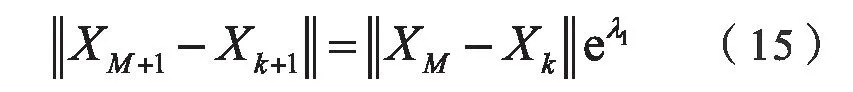
上式即为最大Lyapunov 指数预测模型[6],该式子中,对于点XM+1只有最后一个元素分量未知,从数学方程求解来看是可求的,因此,未来一段时间的负荷是可以预测的。
该预测模型的具体算法思想如下[7]:
1)根据前文中求得的重构相空间的嵌入维数m和延迟时间τ,得到重构相空间:
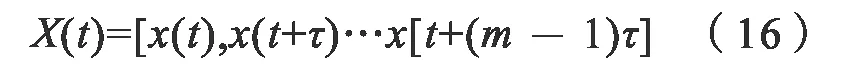
2)结合前文,利用小数据量法计算各序列最大Lyapunov 指数λ1。
3)寻找中心点XM的邻近状态XK并计算d=‖XM-XK‖。
4)根据公式计算XM+1,并根据某种约定算法规则对根进行取舍。
5)将所得预测值带入原序列中,重复上述步骤,直到预测完成。
3.1 预测模型可行性验证
利用该预测模型对理论上的绝对混沌时间序列进行预测,从而判断预测方法的可行性,分别采用Chen's 系统和Lorenz 系统的混沌时间序列进行验证。
1)Chen's 系统验证
Chen's 系统是一个经典的混沌系统[8],其系统方程如下:
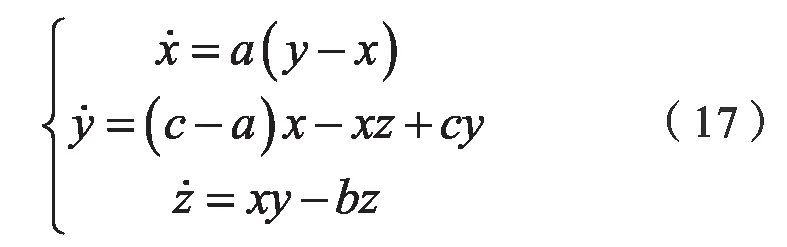
其中取a=35,b=3,c=28。
对于该混沌系统的x分量,用四阶Runge-Kutta 法积分方程组,选择积分步长T=0.001,参数延迟时间取10,嵌入维数取8,进行相空间的重构。利用本节提出的预测模型以前面4800个点对后面200 个点进行预测。其预测结果如图5 所示,由预测结果曲线图可知,该预测模型对Chen's 系统的混沌时间序列的预测效果良好。
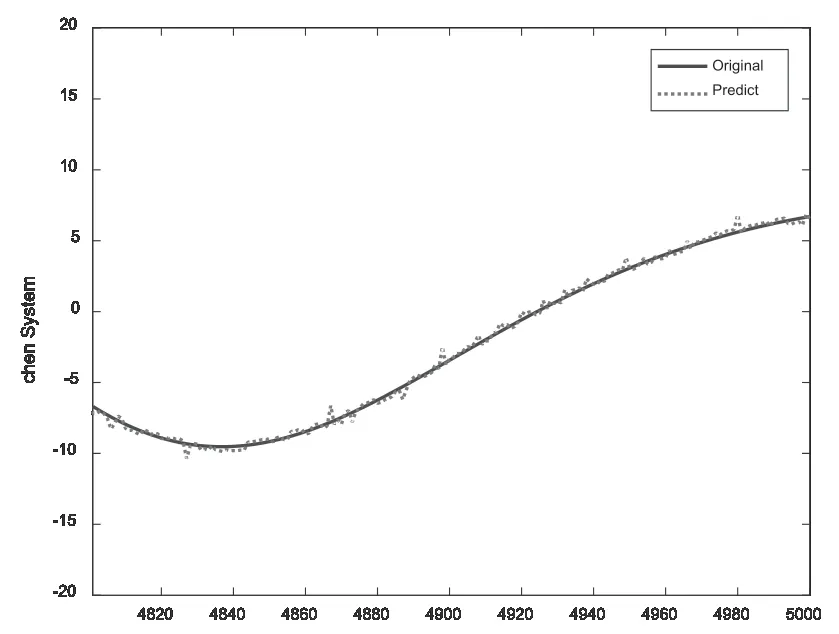
图5 Chen's系统的混沌时间序列预测
2)Lorenz 系统验证
Lorenz 系统方程如下:
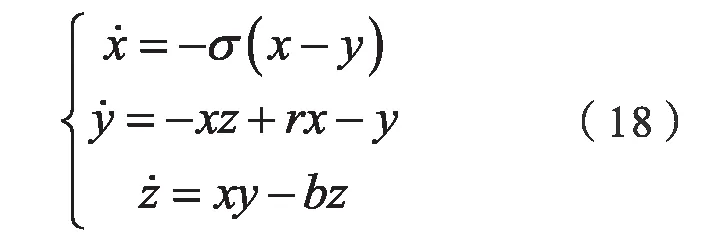
同样,考察该混沌系统的x分量,用四阶Runge-Kutta 法积分方程组,选择积分步长T=0.001,参数延迟时间和嵌入维数分别取17和2,进行相空间重构后。利用最大Lyapunov指数的预测模型以前面4800 个点对后面200 个点进行预测。其预测结果如图6 所示,由预测波形曲线图可知,该预测模型对Lorenz 系统的混沌时间序列的预测效果良好。

图6 Lorenz系统的混沌时间序列预测
3.2 短期负荷预测模型仿真
Chen's 系统和Lorenz 系统两者产生的混沌序列对最大Lyapunov 指数预测模型的验证效果良好。利用该预测模型对郑州市的整点电力负荷时间序列进行研究,时间序列一共1460 个数据,选取了某市2017 年3 月1 日到2017 年4 月30 日19 点的整点负荷,主要思路是以前1440 个数据为预测基准预测后面20 个点(即第1441 小时到1460 小时)的整点负荷进行预测。其中,相空间重构的参数先按照前述方法求得的,取τ=3,m=4,在程序中,对相关参数进行调试,直至找到最佳预测结果。运行程序后,得到的预测结果如图7 所示。
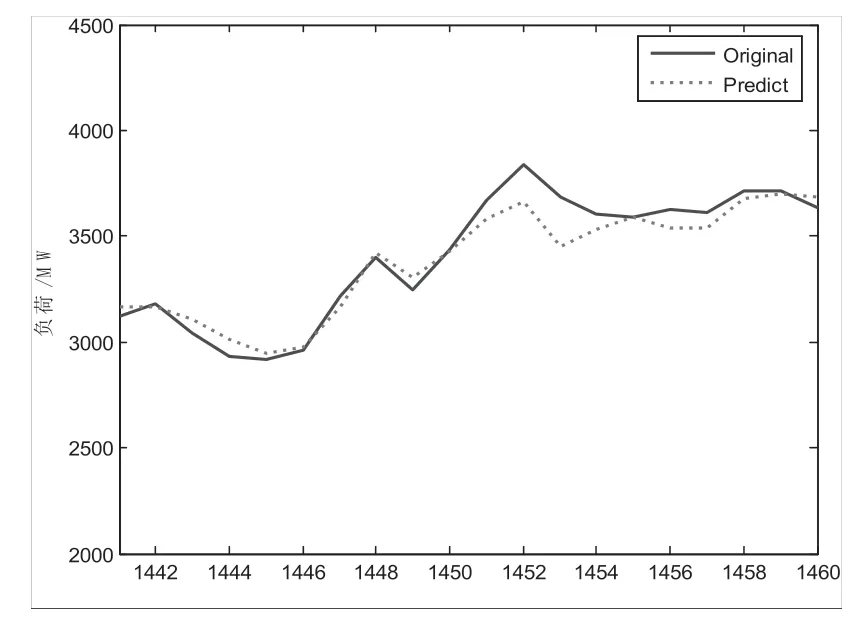
图7 最大Lyapunov模型某市短期负荷预测
由预测曲线可以看出,基于最大Lyapunov指数的预测模型对郑州市电网的短期负荷预测预测效果良好。另外,对于预测的误差计算,我计算的是实际值与预测值二者之间的相对误差,公式如下:
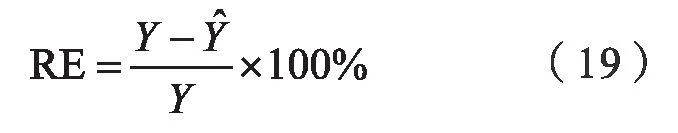
上式中,RE 为相对误差,Y为实际值,为预测值。预测误差曲线如图8 所示。
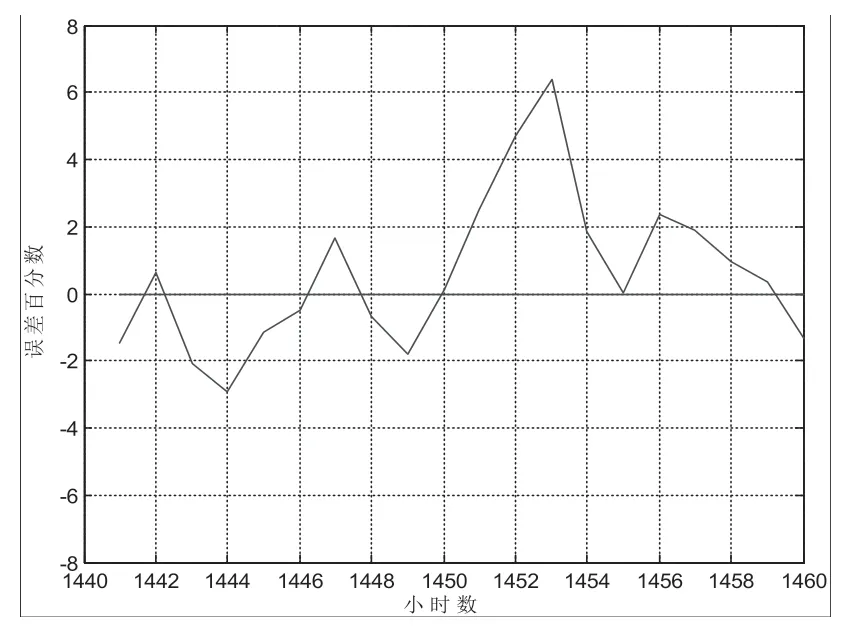
图8 预测的相对误差
由数据可知,预测误差绝对值完全在7%以内,其中误差在5% 以内的占95%,预测误差的最大值为RE=6.374%,预测的最小误差为RE=0.028%。由以上数据分析,可以看出这种预测模型预测出的数据基本满足,预测精度很好。
4 结束语
本文基于混沌理论,采用C-C 算法对重构相空间的参数嵌入维数和延迟时间进行了求解,使用小数据量法求出最大Lyapunov 指数,最终建立了基于最大Lyapunov 指数预测模型,完成了对郑州市2017 年4 月30 日0 点到19 点20 个整点负荷的预测,预测误差绝对值都在7%以内。