一种用于电缆定位的地下电磁波速计算方法

黄继盛，郭平，项恩新，李伟，唐凌云，蔡正杰

（1.云南电网有限责任公司临沧供电局，云南 临沧 677000；2.云南电网有限责任公司电力科学研究院，云南 昆明 650011；3.中国科学院上海微系统与信息技术研究所，上海 201800；4.上海中光华研科技公司，上海 200050）

0 前言

基于电磁波穿透技术的地下目标定位[1]。1904 年，Hulsmeyer 首次利用电磁波穿透探测浅层地下金属物体，利用地下环境中各种介质电参数的差异产生的电磁波回波信号，可以分析地下介质的结构和介质的性质对象的特征。与传统的地球物理方法[2]相比，电磁穿透技术具有抗电磁干扰、探测分辨率高、操作简便、无损检测等优点。20 世纪80 年代，随着计算机和微电子技术的发展，基于电磁波穿透原理的硬件设备的性能得到了提高。与此同时，数据处理的计算机算法[3]也得到了改进，促进了电磁穿透的应用，视场也在不断扩大。从早期探测冰层厚度到探测地下岩土的异常变化，现已深入到工程[4]、空间[5]和考古学[6]等领域。

电磁回波信号处理作为电磁波穿透领域中获取地下目标位置、大小、材质和地下波速信息的重要研究领域，主要通过以下方法实现：

1）电磁场反演方案[7-9]；

2）模式识别方法[10-11]；

3）图像处理方法[12-14]。

其中，图像处理方法以其鲁棒性强、实时性好等优点被广泛应用于地下目标回波信号的自动检测中，并取得了大量的研究成果。特别是感兴趣区域（ROI）的有效提取方法包括：

1）边缘检测方法[15]；

2）霍夫变换[16]；

3）神经网络[17]；

4）信号能量统计[18]。

顶点坐标由对称算法[19]获得，同时波速估计方法有：

1）模式匹配法，

2）特征双曲加权法，

3）基于反射光强度的方法，

4）迭代偏移处理速度等方法。另外，利用双曲线拟合系数可以得到地下目标的半径。

本文采用时域有限差分法对不同介电常数的土壤介质和不同半径的地下目标柱体进行模拟，得到正演双曲信号图像[20]。随后采用自适应高斯阈值法[21]提取特征图像，利用最小二乘法拟合双曲线信号，对目标进行逆定位。考虑到波速对地下目标定位的重要影响，以不同半径的目标和不同介电常数的土壤为例，比较了3种计算波速的方法。

1 理论

根据电磁波的传播和散射原理，通过向地下发射电磁信号，接收地下介质中不连续点散射回来的回波信号，实现对地下目标的成像、定位和量化。均匀土壤模型下的探测过程如图1 所示，图中，地下目标正上方x0位置对应的回波时延为t0，x位置对应的回波时延为t，地下电磁波传播速度为v，地下目标半径为r。检测设备沿水平方向移动。根据地下目标位置与x0、x位置之间的三角关系，得到如下方程：

图1 电磁波穿透探测

变形后得到标准双曲公式：

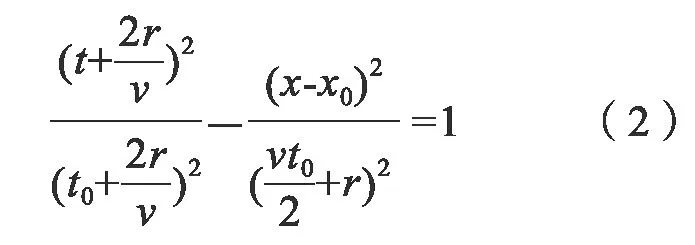
回波信号由有效地下目标信号、内部系统噪声、外部电磁干扰、发射接收天线耦合波、直达表面波等组成。因此，应首先对地下回波信号进行包括降噪在内的预处理。基于统计排序理论的中值滤波方法是一种能够有效抑制噪声的非线性信号处理技术。二维中值滤波器输出为：

式中：f(x,y)和g(x,y)分别是原始图像和处理后的图像，W是二维模板。用平均法去除表面耦合波，其公式如下：

其中M和N是B扫描回波信号的总行数和总列数，B和b表示平均法前后的回波信号。根据以下表达式实现图像分割：

式中：s1(x,y)是部分分割图像，s(x,y)是局部初始图像，t是自适应阈值。

在双曲线区域提取非255 个像素的特征点，得到上、下边缘曲线。利用最小二乘法对双曲线进行拟合，得到双曲线的参数。

根据双曲线公式，双曲线各点的速度为：

利用非加权波速算法，得到波速表达式如下：

当t趋于t0，x趋于x0时，得到的波速v误差较大。因此，采用加权法来减小双曲顶点附近波速的影响。加权系数为：

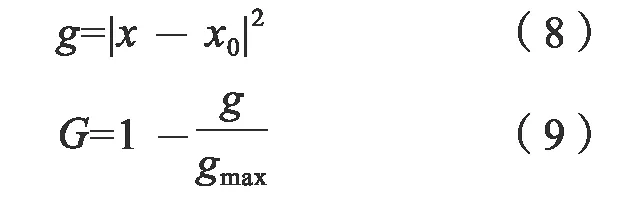
其中gmax是g的最大值，g是相应速度的权重。最终计算的加权波速为：

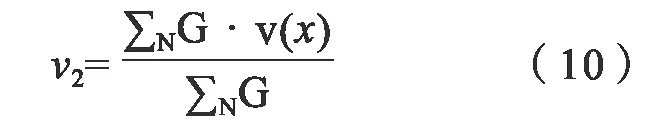
此外，波速值可通过拟合双曲系数获得：

2 模拟

采用时域有限差分法对不同介电常数的土壤介质和不同半径的地下目标进行了研究。然后采用不同的波速估计方法反演目标的定位、半径信息和土壤介质的相对介电常数，研究不同波速计算方法的差异及其原因。如图2（a）所示，模拟面积为2.5 m×1.5 m。0.5 m 厚的绿地是地面以上的空气层。地下黄色区域，厚度1.0 m，为地下土壤介质。土壤的相对介电常数为4.0，电导率为2 ms/m。发射接收天线放置在地面上，距离地面0.5 m，水平方向移动步长0.01 m，频率为500 MHz，入射脉冲为icker 小波，带宽为575 MHz，另有一个半径为0.03 m的地下目标圆柱，水平位置1.25 m，深度0.6 m，材料为pec，模拟模型中的吸收边界条件为完全匹配层（PML），基于时域有限差分数值模拟，经过去除直接耦合波的预处理，得到回波信号，如图2(b) 所示。从图中可以看出，地下目标体回波信号与理论结果一致，呈现双曲线特征。

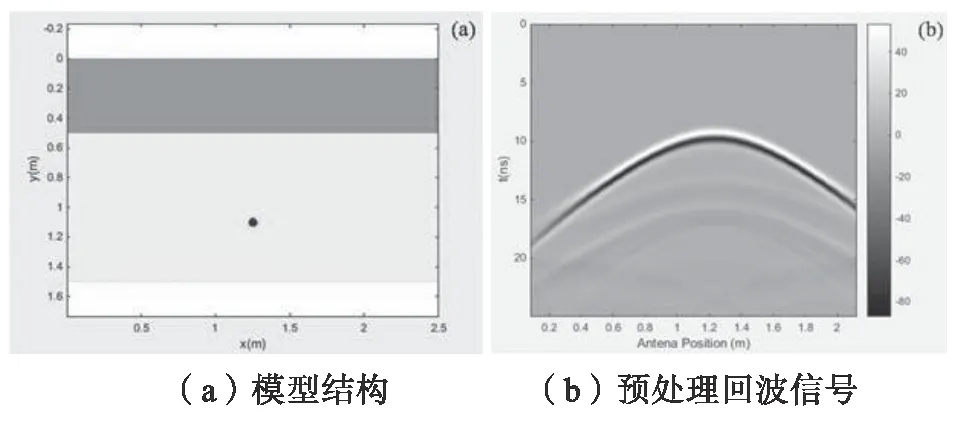
图2 模型结构及预处理回波信号图

图3 显示了本文使用的特征提取方法。图3(a)为输入图像，图3(b)为自适应高斯阈值法提取的双曲线边缘特征，图3(c)为与原始图像比较的双曲线边缘特征，图3(d)为基于最小二乘法的双曲线边缘特征拟合。由此得出的双曲线公式为：

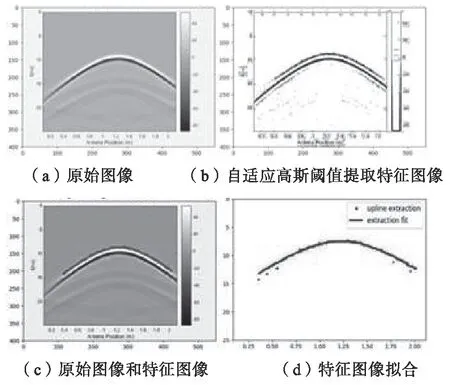
图3 本文使用的特征提取方法

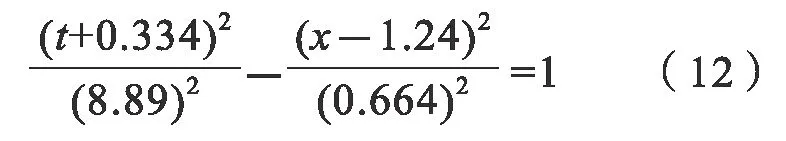
通过拟合双曲线得到双曲线顶点坐标为（1.24 m，8.56 ns）。地下目标的位置和半径取决于波速的计算：

1）非加权波速计算方法得到的波速为0.144 m/ns；

2）加权速度计算法得到的波速为0.145 m/ns；拟合双曲系数得到的波速为0.149 m/ns。根据模拟模型中土壤的相对介电常数为4.0，得到的理论波速为0.15 m/ns。由此可见，上述三种波速计算方法中拟合双曲系数得到的波速值与理论值是一致的。最后，根据双曲线定位坐标和拟合双曲线系数得到的波速值，得到地下目标体的位置为（1.24 m，0.639 m）。该值接近模拟预设值（1.25 m，0.6 m）。另外，通过拟合双曲线系数，计算出地下目标体半径值为0.025 m，接近模拟默认值0.03 m。

分别模拟了半径为0.03 m、0.04 m、0.05 m和0.06 m 的地下目标的波速。图4 显示了以下信息：

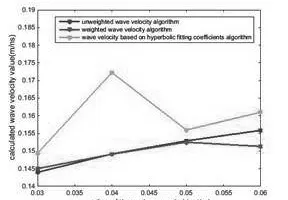
图4 不同半径情况下的波速计算结果

1）从双曲线拟合系数获得的速度在半径0.03 m 处与理论值（0.15 m/ns）非常接近，但在剩余半径处偏差较大，特别是在半径0.04 m 处，这是由于双曲线拟合曲线的不稳定性造成的。

2）由无权波速算法得到的计算半径值与第一种算法相比具有较好的稳定性，计算结果分布在理论值附近。

3）加权速度算法具有稳定性和准确性。这是因为加权速度算法剔除了双曲顶点区域的波速，误差较大。

此外，还研究了上述3 种方法在不同介质介电常数下的介电常数计算值。结果如图5 所示：

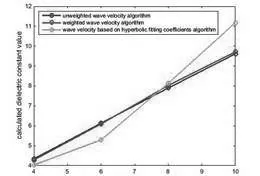
图5 不同土壤相对介电常数模型下的计算结果

1）当土壤介质的相对介电常数为4 和8 时，基于双曲线拟合系数的波速计算方法与理论值吻合较好，而当相对介电常数为6 和10 时，与理论值偏差较大。这种现象与上述不同半径情况相似，说明基于双曲线拟合系数的波速计算方法不够稳定，拟合条件不好时计算值与理论值不一致，影响最终结果。

2）双曲线各点的加权或非加权波速计算值与理论值接近。

为了检验我们的方法的抗噪性，我们使用上述方法根据图6 所示的野外测量信号计算地下目标的埋深，图6 中的双曲线是我们的算法自动识别和提取的双曲线。计算得到的埋深与实际埋深吻合较好，说明该方法具有一定的抗噪声能力。这是由于自适应高斯滤波方法和加权平均方法，有助于抑制随机噪声的影响。

图6 基于现场测量信号的计算结果

3 结束语

本文采用时域有限差分法对不同介电常数的介质和不同半径的地下目标进行了模拟。采用自适应高斯阈值法提取特征图像，采用最小二乘法提取双曲线信息。介绍了3 种不同的波速计算方法。分别研究了3 种波速计算方法对最终反演信息的影响。结果表明，基于双曲拟合系数的波速计算方法稳定性差，当土壤介质的介电常数和地下目标半径发生变化时，计算结果与理论值有偏差，双曲线各点的加权波速计算值与理论值接近。