考虑周期性的城市道路车流量预测模型

李鹏程

(中远海运科技股份有限公司，上海 200135)

0 引 言

城市道路车流量预测是交通领域的研究热点之一。准确预测车流量，能使交通管理部门提前对未来的交通运行状况做出判断，在制订交通管控和诱导预案时具有可靠的数据支撑，最终达到缓解交通拥堵、节约出行时间和提高出行效率的目的。有效解决交通拥堵问题有助于减少交通事故、环境污染和能源浪费，因此对车流量进行预测具有重要的现实意义。已有很多学者采用不同方法捕捉车流量规律，建立预测、分析模型，其中差分自回归移动平均(Autoregressive Integrated Moving Average，ARIMA)模型是比较基础、常用的模型，广泛应用于车流量等时间序列数据的分析中。然而，ARIMA模型在分析历史车流量规律时忽略了周期性因素。所谓周期性，是指流量在特定时期(年、季度、月、周和节假日等)内表现出相似的变化趋势或具有相当的水平。

目前，研究人员[1-4]已在船舶交通流量、空中交通流量、轨道交通客流量和交通枢纽客流量等领域建立多种考虑季节性和周期性因素的模型。在道路交通流量预测方面，很多研究都表明，考虑过去一定周期内的变化规律的模型能更准确地预测未来的车流量。祁伟等[5]认为交通流数据存在很强的周期性，采用考虑季节性的ARIMA模型能得到很好的预测效果；张建晋等[6]指出城市交通流量数据具有较为明显的以天或周为周期的统计学特征；孙湘海等[7]通过研究发现，考虑日周期性和周周期性的模型预测城市道路短期交通流量的能力最强，且不同周内的交通流变化具有相似性，若没有特殊事件的影响，每周相应日的流量存在共性。然而，在这些研究中：文献[5]和文献[7]只是将模型应用于稀疏交通流的预测中，未对其在常规车流量预测中的适用性进行研究；文献[6]建立的模型较为复杂，对预测结果解释的能力有待提升。本文考虑对常用的ARIMA模型进行优化，将其应用于日常的车流量预测中。建立考虑周周期性(周期为7 d)的ARIMA模型，分析周期性规律对车流量预测效果的影响。

本文提出的方法除了能用来预测城市车流量以外，还能应用于数据存在相似规律的其他业务中。目前已依托某城市公路管养平台积累大量养护数据，若本文提出的模型经验证有效，可直接将其应用于实际业务中，比如预测道路养护投诉量等。

1 数据来源及建模流程

1.1 数据来源及统计分析

本文建模所用车流量数据来源于广东省政府的开放平台。以某条城市道路的车流量日统计数据为例建立ARIMA模型，验证考虑周周期性的模型具有更好的车流量预测效果。由于ARIMA模型要求原始数据具有平稳性，且本文还将研究车流量的周周期性，因此对车流量数据有一定的要求。考虑到数据缺失值较多时无法用于建模，加上开放平台的数据具有延迟性，本文选用某年10月至次年4月的车流量数据(共27个完整周期(1个周期7 d)，193条连续日期的数据)进行分析，无缺失值。对原始车流量数据进行描述性统计分析，结果见表1。从表1中可看出：10月份的车流量最大，平均日车流量为5 728辆；4月份的车流量最小，平均日车流量为1 819辆。日车流量最大为15 166辆，最小为379辆；月度车流量呈不平稳变化规律。

表1 原始车流量描述性统计分析结果

1.2 ARIMA模型构建流程

ARIMA模型由自回归(Autoregressive，AR)模型和移动平均(Moving Average，MA)模型2部分组成。

1)AR模型利用历史车流量预测当前的值yt(t为时间,d)，p阶自回归模型AR(p)代表yt的值与之前的p个值有关，表达式[8]为

yt=α0+α1yt-1+α2yt-2+…+αpyt-p+εt

(1)

式(1)中：α0为常数；εt为误差项；α1，α2，…，αp为回归系数。

2)MA模型表示车流量与其误差项之间的线性关系，q阶移动平均模型MA(q)代表yt与误差的回归，表达式[8]为

yt=β0+εt-β1εt-1-β2εt-2-…-βqεt-q

(2)

式(2)中：β0为常数；β1，β2，…，βq为回归系数。

因此，ARIMA模型的表达式[8]可表示为

yt=γ0+α1yt-1+α2yt-2+…+αpyt-p+εt-β1εt-1-β2εt-2-…-βqεt-q

(3)

式(3)中：γ0为常数。

ARIMA模型构建步骤见图1。在建立ARIMA模型时，要求时间序列是平稳的。所谓平稳，是指所有车流量值都围绕某一水平直线上下波动。然而，大多数时间序列数据都是不平稳的，因此要先对原始车流量数据进行平稳性检验。平稳性检验的方法主要有序列图和自相关图等[9]。若原始车流量数据为非平稳时间序列数据，则需对其进行差分。差分是使时间序列平稳化的常用方法，用后值减去前值，以消除前后数据之间的依赖性[10]。进行差分的次数d称为阶数，由于每次差分都会引起信息损失，差分值次数一般不超过2次[11]。

图1 ARIMA模型构建步骤

将原始车流量数据转化为平稳时间序列数据之后，需通过自相关图和偏自相关图中的拖尾步数，大致确定ARIMA(p，d，q)模型中p和q的值，该过程即为模型定阶过程。

此后，进行参数估计和检验，其中检验主要是进行白噪声检验，根据杨-博克斯Q检验结果的显著性，判断残差是否属于白噪声序列。当显著性大于0.05时，认为模型提取的信息比较充分，可接受。此外，还要根据p和q取不同的值时ARIMA(p，d，q)模型的拟合指标，确定使模型最优的p和q的值，即确定最优模型。

对于不同的模型，主要根据以下2个指标选择最优模型：

1)平稳R方。R方为原始车流量数据的模型决定系数，其取值范围为小于等于1，取值越大，代表模型的拟合优度越好。平稳R方的取值范围与普通R方完全相同，但其是采用模型的平稳部分进行计算的，当原始车流量数据具有周期性波动特征时，该指标优于普通R方。

2)正态化BIC。正态化BIC是基于均方误差的分数，考虑罚分和序列长度，其值越小，代表模型越好。

2 ARIMA模型构建

本文采用SPSS 26.0软件绘制车流量序列图、自相关图和偏自相关图，并进行建模预测等，车流量序列图见图2。

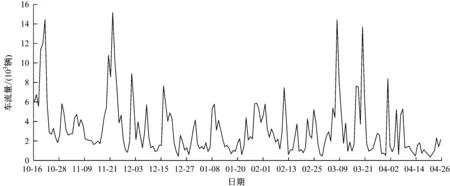
图2 车流量序列图

由图2可知，原始车流量数据呈上下波动，且大致在每周都有1个车流量高峰日，可能存在周周期性特征，不满足ARIMA模型的平稳性要求，因此需先对原始数据进行差分处理。进行1次差分处理之后，车流量序列去除了长期趋势，围绕均值上下波动，认为序列达到了平稳要求，可确定差分次数d=1，继续进行ARIMA(p，1，q)模型构建。图3为1阶差分之后的车流量序列图。

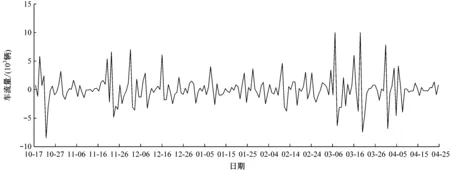
图3 1阶差分之后的车流量序列图

根据自相关图和偏自相关图(见图4)确定ARIMA(p，1，q)模型中p和q的值。由图4可知：在偏自相关图中，在1阶时超出置信区间，1阶拖尾，可确定p=1；在自相关图中同样如此，可确定q=1。由此，可建立ARIMA(1，1，1)模型。

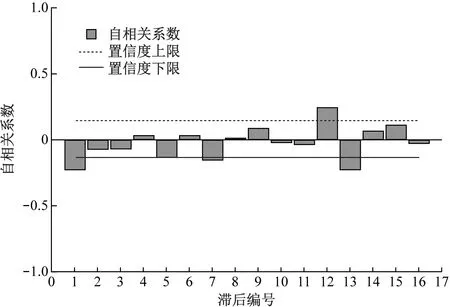
a)自相关图

利用SPSS软件的时间序列预测模块，选择车流量作为因变量，建立ARIMA(1，1，1)模型并进行参数估计，得到一系列模型拟合指标，见图5。由图5可知，模型ARIMA(1，1，1)的拟合优度较差，仅为0.198，且杨-博克斯Q检验显著性为0.014，小于0.050，说明建立的ARIMA模型未通过白噪声检验，模型中还忽略了有用的信息。根据各种车流量预测研究中对周期性和季节性的总结，本文认为该ARIMA模型的拟合优度较差，可在模型中考虑周周期性对车流量的影响，建立新的ARIMA模型。

3 考虑周期性的ARIMA模型构建

下面在上述ARIMA(1,1,1)模型的基础上考虑周期性因素，建立ARIMA(1,1,1)(P，D，Q)S模型，其中S为周期。由于考虑的是周周期性的影响，因此S=7。ARIMA(1,1,1)(P，D，Q)7的建模流程与ARIMA(1,1,1)相同，需先确定差分次数D，再确定P和Q，最后进行建模和白噪声检验。图6为1阶季节性差分后的车流量序列图。由图6可知，进行1次季节性差分处理之后，序列围绕0值波动，D=1。

图6 1阶季节性差分后的车流量序列图

利用SPSS 26.0软件得到经过1次差分和1次季节性差分处理之后的自相关图和偏自相关图，见图7。通过观察发现，P和Q均不超过3[7]。依次建立P=0，1，2，3和Q=0，1，2，3的ARIMA(1,1,1)(P，1，Q)7模型，比较各模型的拟合优度、正态化BIC和杨-博克斯Q检验结果，选出最优模型。建立的5个ARIMA(1，1，1)(P，1，Q)7模型指标拟合结果见图8。

a)自相关图

e)ARIMA(1,1,1)(1，1，1)7模型

由图8可知：ARIMA(1,1,1)(0，1，1)7、ARIMA(1,1,1)(0，1，2)7、ARIMA(1,1,1)(1，1，2)7和ARIMA(1,1,1)(2，1，1)7等4个模型的拟合优度较好，分别达到了0.567、0.572、0.574和0.573，但这4个模型的杨-博克斯Q检验结果的显著性分别为0.044、0.049、0.044和0.045，均小于0.050，说明这4个模型都未通过白噪声检验，建立的模型不够好。通过比较，最终选定拟合优度和杨-博克斯Q检验结果显著性均较好的ARIMA(1,1,1)(1，1，1)7模型为最优模型。该模型的拟合优度平稳R方达到了0.573，相比之前的模型有很大的提高；杨-博克斯Q检验结果的显著性为0.056，大于0.050，说明该模型通过了白噪声检验。考虑周期性特征的ARIMA(1，1，1)(1，1，1)7模型明显优于ARIMA(1,1,1)模型。

最后，利用建立的ARIMA(1，1，1)(1，1，1)7模型对4月23日—4月26日的车流量进行预测，并将所得结果与实际车流量相对比。ARIMA(1，1，1)(1，1，1)7模型车流量预测结果见图9。从图9中可看出，预测车流量与实际车流量的整体变化趋势大致相同，在预测的4 d中，除了4月25日的预测效果与实际有较大差距，另外3 d的预测结果良好。这说明该模型适合预测较短天数内(即前2 d)的车流量，预测天数变长时预测效果会变差。结合拟合优度平稳R方达到了0.573的较高水平，认为建立的ARIMA(1，1，1)(1，1，1)7模型较好。

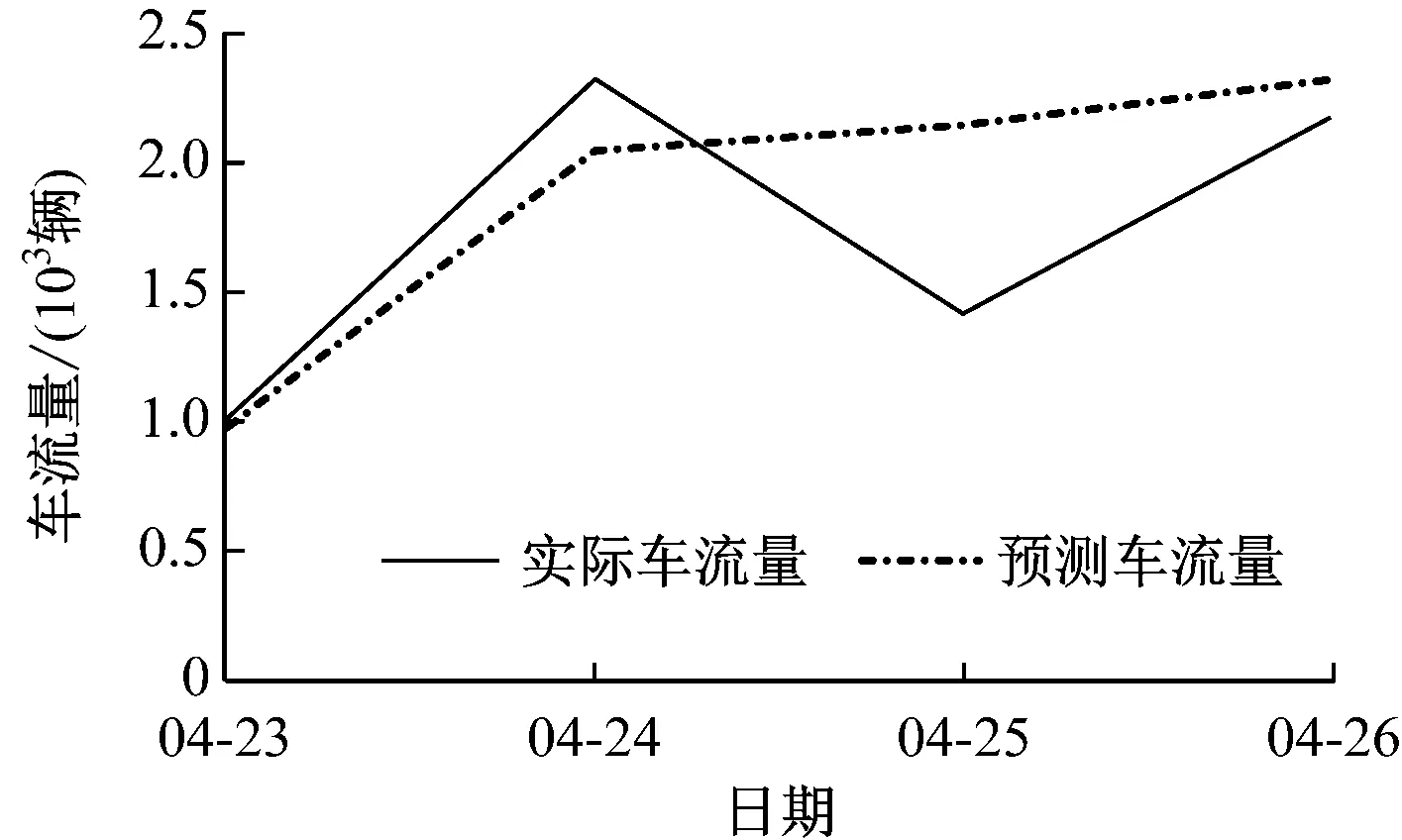
图9 ARIMA(1，1，1)(1，1，1)7模型车流量预测结果

4 结 语

本文建立了考虑周期性的ARIMA(1，1，1)(1，1，1)7模型，得出的拟合优度相比原始的ARIMA模型有很大提升。因此，在进行车流量预测过程中，不能忽略可能存在的周期性或季节性特征的影响。但是，本文建模采用的数据量较小，模型包含的车流量影响因素单一，后续可尝试建立考虑不同输入变量的ARIMA模型，以不断提高模型的预测精度。此外，本文验证了提出的考虑周期性的车流量预测模型在城市车流量预测方面的有效性，当道路管养、养护等业务中涉及类似与时间序列相关的数据时，可直接利用本文的建模思路和方法快速实现对养护数据的预测分析，产生新的养护应用场景。