基于光放大法测量金属线膨胀系数

周婷倩，吴心田，谭 闯，张耀婷，刘宵彤，马舒然，李晓丹，张子洋，于伟威

(辽宁师范大学 物理与电子技术学院，辽宁 大连 116029)

金属具有光泽、良好导电、导热、延展的性质，在生活中的应用极为普遍，常用于机械零件制作和工程建设。在温度改变时，由于物质热胀冷缩的原理，金属在受热的情况下其体积会发生微小的形变，对于某些精密仪器，需要严格控制热形变量。为方便测量金属的线膨胀系数，人们通常采用线膨胀系数来衡量金属在受热的情况下发生形变的程度[1]，即固体物质在升高1 ℃时，物体一维方向上的相对改变量。在测量范围不大的情况下，线膨胀系数可以认为是一个常数，数量级一般在10-5℃-1[2]，即一根一米长的金属棒温度升高10 ℃后，材料伸长约0.1 mm。金属材料线膨胀系数的测量被广泛应用于加工材料、器械制造和设施修筑工程等方面，在工程上具有重要的意义[3]。通常采用微位移传感器，如利用霍尔传感器[4,5]，通过电信号测量长度的微小变化来计算线膨胀系数；或者运用光学方法，如利用迈克尔逊干涉[6,7]，将测量长度的微小变化转换为测量干涉频带来计算线膨胀系数。但由于微位移传感器操作较为复杂，受实验者的操作等因素的影响较多，测得的结果往往很不理想，产生的误差较大；应用迈克尔逊干涉时，实验的仪器组装精度要求较高，对实验者的操作能力要求较高，两者都很难达到，所以对实验数据的影响较大。以上方法在具体实验中难以实现，而光放大法仪器较易组装，操作简便，因此，本文从光放大原理这一方向进行实验。

文章将光放大原理用到金属受热时产生的微小形变的测量上，并结合几何光学和热力学公式计算出金属的线膨胀系数。利用激光源发出的激光经过平面镜反射后形成的放大光路把金属受热时产生的微小形变放大，通过加热前后光路的反射角度、光屏移动前后光斑位置的几何关系和光斑移动的距离，来计算金属的微小形变量。使用该方法进行实验，实验现象更为明显，测量数据更加精确，从而得到较为准确的金属线膨胀系数，提高了测量的精确度，并且实验的方法简单，容易操作。

1 实验原理

1.1 光放大原理

金属受热会膨胀变形，但是在加热金属时，肉眼几乎观察不到它的变化，这是因为金属的线膨胀系数十分微小，一般在10-6数量级。例如，黄铜在50～500 ℃温度区间的线膨胀系数在16.00×10-6℃-1和18.00×10-6℃-1之间。可见，仅靠肉眼观察很难看出这样微小的形变，想要测量这样的形变更是不易，因此，采用光放大原理将金属微小形变进行放大，增强其实验现象。

光放大方法是一种测量微小形变的方法，是普通物理实验中常用的方法。光放大原理[8]的示意图如图1所示，它通常利用平面反光镜对光线的反射角度变化来放大物体形变前后的位移变化从而实现测量。使由激光源所发出的一束激光垂直入射到与激光源距离为L的平面镜上，此时反射光和原光束重叠，当放置平面镜的桌子发生形变，使得平面镜倾斜了一个角度θ，反射光将不再与入射光重合而在其上方或者下方产生光斑，这说明桌子产生了形变，形变大小与L有关。设光点产生偏差d，则θ=0.5arctan(d/L)。

图1 光放大原理示意图

1.2 金属热膨胀系数的测量原理

以铜片为研究对象，基于光的反射定律，利用光放大原理来测量铜片加热后的微小形变。

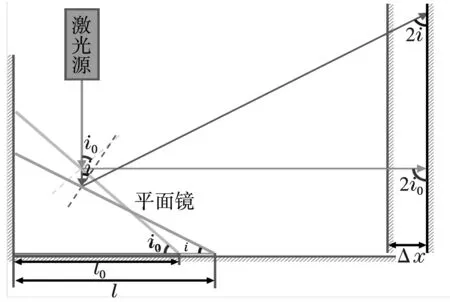
图2 实验装置示意图

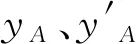
(1)

即

(2)

可得到未加热时铜片的线长度l0：

l0=Lcosi0

(3)

(4)

(5)

得到加热变形后的铜片线长度l：

l=Lcosi

(6)

Δl=Lcosi0-Lcosi

(7)

(8)

经上式可得出该铜片的形变长度及其线膨胀系数。因实验要求出相对误差，所以给出相对误差公式：

(9)

2 实验方法

2.1 实验装置

金属片(铜、铝、钛)、加热台、反光镜、激光源、铁架台、光屏、挡板，铁块。如图3为实验装置图：

图3 实验装置图

2.2 测量方法

将金属片放在加热台上，一端靠在实验装置的竖直挡板上，紧贴另一端放置一个铁块，打开激光源，将平面镜放在装置上，一端靠在铁块边缘，另一端靠在竖直挡板上，光屏上将呈现光斑。记下光斑和光屏的位置，并将光屏向加热装置所在的方向上移动一段距离，再次记下光斑的位置和光屏的位置。取下平面镜和铁块，打开加热台，将金属片加热到一定温度后，以同样的方式放置铁块和平面镜，记下在加热前后的两个位置下光斑在光屏上的位置。重复以上实验步骤，将数据带入公式中计算金属片的线膨胀系数。

3 实验结果与分析

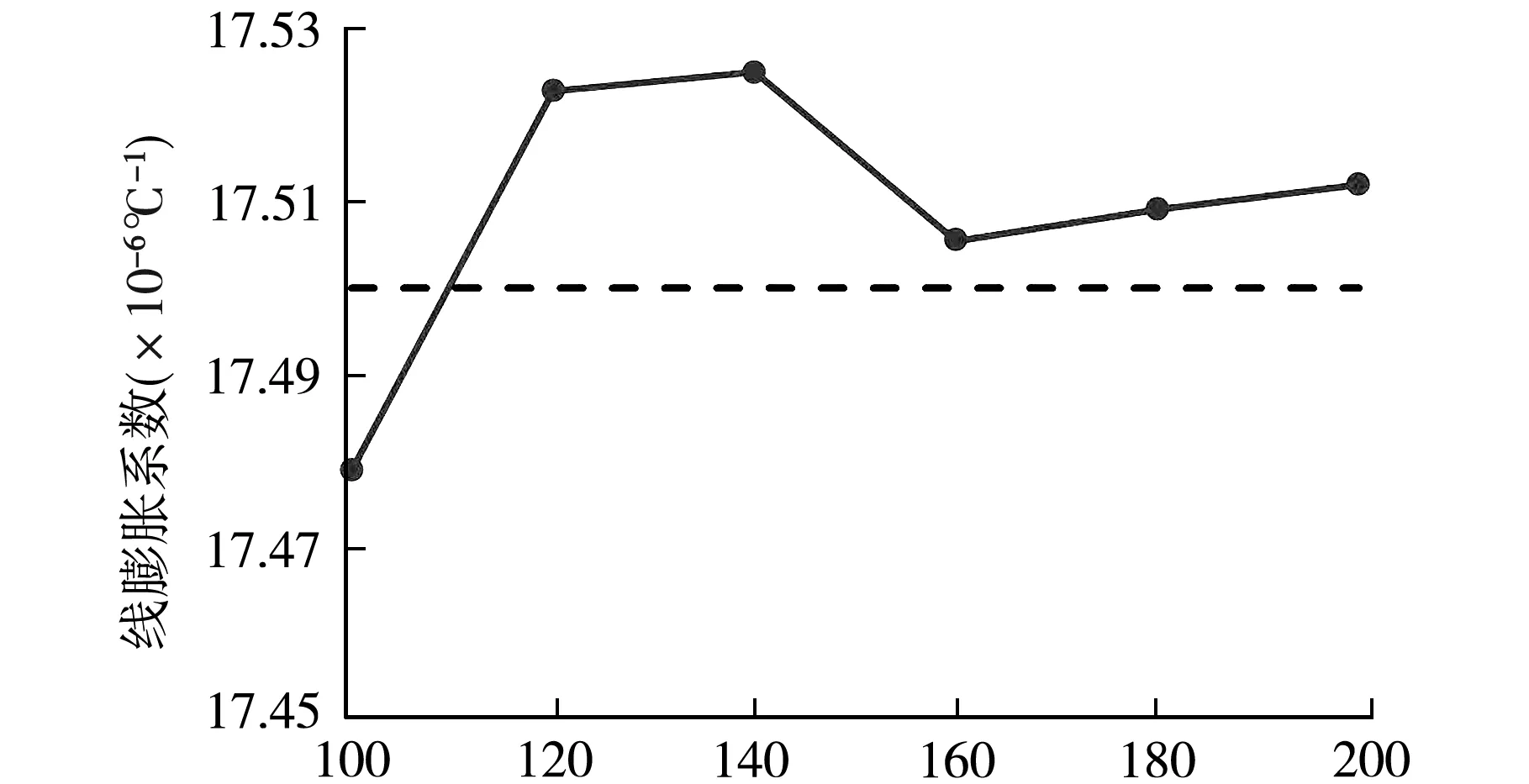
首先以铜为例，探究金属的线膨胀系数，金属的线膨胀系数在温度变化不大的范围内基本固定[9]，实验通过测量末态光屏移动的距离和末态角度求出金属铜的形变量，根据公式(8)求出铜的线膨胀系数，实验选用的平面镜长度为L=25.000 cm，铜片的原长为l0=15.000 cm，以铜片加热前后的温度差为自变量，以20 ℃为梯度，分别测量计算6组不同温度变化下的铜的线膨胀系数，每组各测量5组数据。最终得到以下测量数据：

表1至表4分别为ΔT=100 ℃，120 ℃，140 ℃，160 ℃下，各次实验末态光屏移动的距离、末态角、金属形变量并利用公式(9)求得线膨胀系数与铜参考真值α0=17.50×10-6℃-1的相对误差。由上述表1至表4可得出，铜的线膨胀系数平均值分别为17.48×10-6℃-1，17.52×10-6℃-1，17.53×10-6℃-1，17.50×10-6℃-1，平均相对误差分别为0.42%，0.22%，0.21%，0.18%，实验测得的线膨胀系数数据平均值与理论值α0=17.50×10-6℃-1很接近，实验数据波动幅度较小，与理论值较为贴合。并且最大相对误差均小于1.00%，实验数据可信度高，表明实验室环境下也可以较为准确地探究金属铜的胀缩物理特性。

表1 ΔT =100 ℃下铜线膨胀系数的测量数据

表2 ΔT =120 ℃下铜线膨胀系数的测量数据

表3 ΔT=140 ℃下铜线膨胀系数的测量数据

表4 ΔT=160 ℃下铜线膨胀系数的测量数据

如图4所示，蓝色实线为ΔT=180 ℃铜线膨胀系数的测量数据，蓝色虚线为ΔT=180 ℃铜线膨胀系数的相对误差值；橙色实线为ΔT=200 ℃铜线膨胀系数的测量数据，橙色虚线为ΔT=200 ℃铜线膨胀系数的相对误差值，横坐标为实验次数，左侧纵坐标表示线膨胀系数大小，右侧纵坐标表示相对误差。由此可以得到在ΔT=180 ℃下，铜的线膨胀系数平均值为17.51×10-6℃-1，平均相对误差为0.16%，最大相对误差为0.29%，最小相对误差为0.03%；在ΔT=200 ℃下，铜的线膨胀系数平均值为17.51×10-6℃-1，平均相对误差为0.18%。最大相对误差为0.34%，最小相对误差为0.05%。

图4 ΔT=180 ℃和ΔT=200 ℃铜线膨胀系数的测量数据及误差

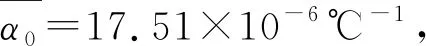
ΔT/℃

图6 金属铝的线膨胀系数的测量数据及误差

由于金属钛的熔点也非常高，并且相对容易获得，在生活中也有一定的应用价值，因此将实验继续推广到金属钛，利用相同的方法计算金属钛的线膨胀系数。通过测量末态光屏移动的距离和末态角度求出钛金属的形变量，再根据公式(8)求出钛的线膨胀系数，得到图7。

图7 金属钛的线膨胀系数的测量数据及误差

光放大法能够对各种常见金属进行推广，得到不同金属的线膨胀系数，实验数据均与理论值相差不大，平均相对误差均小于1.00%。实验的线胀系数数据能够反映金属热胀冷缩的物理特性，该特性是金属的固有属性，大多情况下该系数为正值，在温度变化不大的情况下该系数基本不发生变化，以上3种金属铜、铝、钛均为常见金属，对它们的线膨胀系数进行测量能够进行材料矿物分析、微裂纹的愈合和扩展等研究，可以应用到生活中的工业制造等方面。

4 结 语

金属的线膨胀系数反映了金属由于温度改变而胀缩的能力。利用易于操作的光放大原理，推导出了光斑移动距离与金属伸长量的函数关系，根据该关系从而得到金属线膨胀系数的计算公式，再利用该公式测量相关物理量，计算金属的线膨胀系数。首先用金属铜进行实验，探究出温度变化量基本不会改变其线膨胀系数；并将实验由金属铜推广到其他金属铝和钛，利用实验室简易装置进行测量，并通过计算得出结论：在温度变化不大时，金属的线膨胀系数基本固定，与标准值很接近，相对误差在0.02%～0.90%范围内，测量精准度高，实验数据可信度高。通过对金属线膨胀系数的测量，反映了金属的固有属性，在生产生活中可广泛应用于加工材料、器械制造和设施修筑工程等方面，在工程上具有重要的意义。