桥梁墩台垂直度简易测量方法

陆治屹

(广西交通工程检测有限公司，广西 南宁 530222)

0 引言

在桥梁施工以及运营过程中，都会涉及墩台垂直度测量。墩台垂直度可以解释为墩台顶的水平位移偏差，即墩台的顶端水平位置与低端水平位置的差值；如果使用全站仪等角度测量体系，则可以解释为墩台的倾斜角度。目前规范要求的测量方法为垂线偏差测量和全站仪倾斜测量。垂线法至少需要两名技术人员操作，桥上人员放置垂线，桥下人员测量，这种方法在风力较大的情况下，测量误差较大；全站仪比较笨重，且需要配备三脚架，而桥梁建设往往跨越山谷或河流，地理条件复杂，在测量过程中需要翻山越岭，跨越河流、山谷等，并且需要寻找合适的仪器架设地点，给测量工作带来较大困难[1-2]。

秉承减少人力、适应现场环境、降低工作难度的初衷，本文探究并设计一种以激光测距仪为核心的墩台垂直度简易测量方法，该方法降低了现场工作难度，提高了工作效率，对环境适应性极强，可在桥梁建设中推广应用。

1 基本原理

该方法基本原理为：使用激光测距仪测量出工作点到桥梁墩台顶端及底端距离，并配合角度尺测量出工作点到测量点的水平夹角，最终推算出桥梁墩台的倾斜度。该系统结构为将水准泡固定于角度尺上，使水准泡与角度尺呈零刻度水平，并将激光测距仪与角度尺连接，使激光测距仪只能沿角度尺竖直方向转动。该简易测量方法系统结构如图1所示[3]。

2 应用及计算

现场工作中，为减少人为误差，确保测量精度，可将测量系统垂直固定在标杆上，或固定于现场任意固体上，调整系统使水准泡水平居中，确保系统处于水平。用激光测距仪测量工作点A与墩台底部B的距离AB，并读取激光测距仪与角度尺夹角∠α1，再用激光测距仪测量工作点A与墩台顶部C的距离AC，并读取激光测距仪与角度尺夹角∠α2，如图2所示[4]。

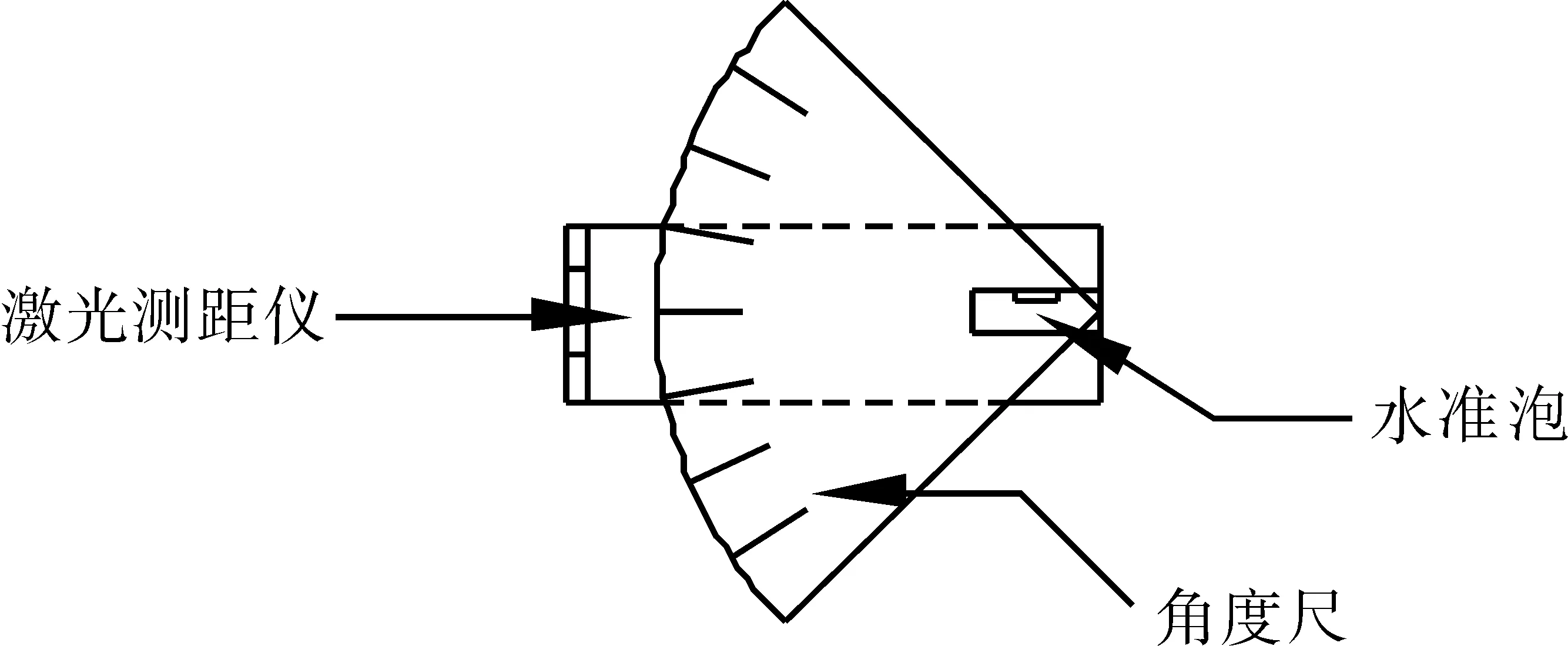
图1 简易测量系统结构示意图

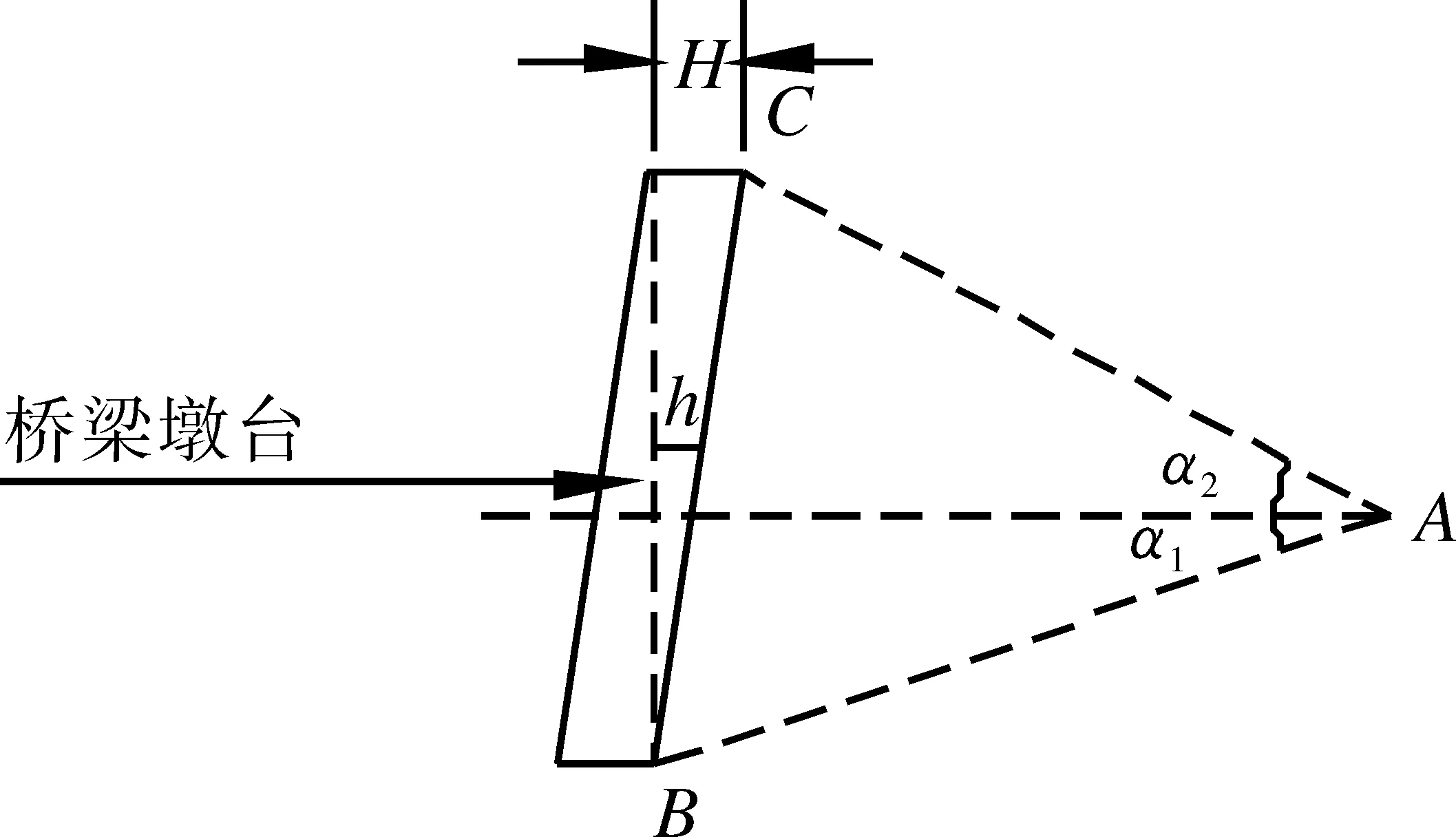
图2 测量过程示意图

根据余弦定理：

BC2=AB2+AC2-2AB×AC×cos(∠α1+∠α2)

(1)

由此可得桥梁墩台底部到顶部距离BC，再根据正弦定理：

(2)

由此可得：

(3)

其中AB、AC、∠α1、∠α2均为测量数据。桥梁墩台的理论轴线与测量系统零角度线夹角为90°，由此，最终可计算得倾斜角∠h及桥梁墩台偏差值H。

∠h=90°-∠ABC-∠α2

(4)

H=BC×sin∠h

(5)

3 误差分析

在测量工作中不可避免地会产生误差，其中包括系统误差、人为操作误差等，本方法系统的误差主要包括激光测距仪的系统误差和水准泡对准居中的误差。

手持式激光测距仪重量轻、体积小、操作简单，其基本原理是测量光往返目标所需要的时间，结合光速及大气折射系数计算两点距离。光速是固定的，所以其精度主要取决于仪器的测时精度。

现有的手持式激光测距仪中，例如深达威SW-M50以上系列手持式激光测距仪，其精度可以达到1.5 mm ±(D×0.05‰)，也就是每增加10 m的距离，误差增加0.5 mm，每增加20 m距离，误差增加1.0 mm。除了一些超高墩外，桥梁桥墩高度普遍在10 m左右，不考虑激光测距仪固有的1.5 mm系统误差的情况下，测量误差是0.5 mm；考虑激光测距仪固有的1.5 mm系统误差情况下，误差在2 mm内，这与垂线法测量中使用钢直尺的1 mm精度接近。

水准泡的精度即为角值，是指气泡由中心线向任意方向移动2 mm的倾角。目前测量工作中常用的是长水泡和圆水泡，其中长水泡可以达到20″/2 mm。在日常工作中基本上能保持水准泡在2 mm内。

假定墩高为10 m，工作点到桥墩底及桥墩顶的距离都是10 m，工作点与桥墩顶及桥墩底的夹角都是30°，桥墩未有倾斜即倾斜角为0°，垂直度偏差值为0 mm；假设第一次测量水准泡居中，第二次测量水准泡偏移2 mm，即偏差20″，并且在不考虑水准泡未居中对激光测距测量值的影响的情况下，由式(3)计算可得：

59°59′50″

若误差角是∠α1，则由式(4)计算可得：

∠h=90°-59°59′50″-30°0′20″=-10″

若误差角是∠α2，则由式(4)计算可得：

∠h=90°-59°59′50″-30°=10″

由式(5)计算可得：

H=10×sin10″=0.5 mm

由计算结果可知，不论误差是产生在∠α1还是在∠α2，最终的误差都是10″，垂直度偏差值为0.5 mm。

以上误差计算值并未考虑倾斜带来的测距影响。若考虑测距影响，倾斜对测距的影响大约是2 mm。4种不同情况下的单次倾斜误差计算结果见表1。由表1可知，误差最大的情况是测量C点时倾斜的情况，偏差角度Δ∠h为46″，偏差值ΔH为2.2 mm。

表1 单次倾斜误差计算结果表

在两次测量水准泡均未居中，并向同一个方向倾斜的情况下，这可以认为两次的工作点在同一个位置上，所以并没有产生误差。

当两次测量水准泡均未居中，并向不同的方向倾斜，这是误差最大的情况。假设测量B点时后倾，那么∠α1增大20″，测量数据是30°0′20″，AB测距约减小2 mm，测量数据是9.998 m；C点时前倾，那么∠α2增大20″，测量数据是30°0′20″，AC测距约增大2 mm，测量数据是10.002 m，反之则测量数据相反。两种双向倾斜误差计算结果见表2。

表2 双向倾斜误差计算结果表

由表2可知，在双向倾斜的情况下，误差值是最大的，偏差角度△∠h为71″，偏差值ΔH为3.5 mm，但是这种人为误差情况可以通过多次测量来避免。因此，系统测量能够产生的误差通常是单次倾斜误差，即最大误差角度为46″、垂直度误差为2.2 mm，而且同样可以通过多次测量来降低这个误差。按照规范要求5 m

4 优势对比

相对于垂线法，本方法减少了技术人员的投入，只需要一名操作人员即可完成测量工作，且受外界环境干扰小。在风力较大的情况下，垂线法甚至可能无法满足工作需求，所以本测量方法从环境适应性上来说优于垂线法。

相对于全站仪测量法，本方法只需要一名技术人员携带手持式激光测距仪、角度尺、水准泡及一根小型标杆即可完成测量工作。在现场工作条件恶劣的墩台垂直度测量工作中，减轻了技术人员的负担，不需要为了寻找合适的仪器架设地点而浪费时间和精力，极大地提高了工作效率。

5 结语

桥梁墩台垂直度简易测量方法是一种以激光测距仪为核心的、方便快捷的垂直度测量方法，其能够满足现行规范的要求，不仅节省了技术人员的投入，降低了现场工作难度，更重要的是对环境的适应性极强。运用此方法对桥梁墩台垂直度进行测量，不仅降低了经济成本，同时极大地提高了工作效率，是一种高效可行的方法。