径向基神经网络在斜拉索损伤识别中的应用研究

奉文明，王 华

(1.广西新发展交通集团有限公司，广西 南宁 530029；2.广西交科集团有限公司，广西 南宁 530007)

0 引言

随着经济的飞速发展，大跨斜拉桥因其简洁美观、受力性能和经济性能优越等特点，在我国得到了广泛的应用[1-3]。其中斜拉索作为斜拉桥的重要受力构件，其结构损伤将严重影响桥梁的安全性和可靠性[4-5]。因此，为了保证斜拉桥的安全运营，保证国民的生命财产安全，研究斜拉索的损伤识别问题具有重要的意义。

关于斜拉索损伤识别的问题，众多学者做了广泛的研究。杨杰等[6]基于BP神经网络并结合北汊斜拉桥拉索损伤数据对斜拉索进行了损伤识别研究，结果表明该方法能有效识别斜拉索的损伤状态。李延强等[7]结合小波包分析和支持向量机建立了斜拉索损伤识别方法，并通过工程实例验证该方法应用于斜拉索损伤识别的可行性。谭冬梅等[8]通过对温度挠度数据构建一元线性回归模型作为损伤指标开展了斜拉索损伤识别研究。邢心魁等[9]引入曲率模态理论和灰度理论对某三塔四跨斜拉桥的拉索进行了损伤识别研究，研究结果可为该桥维护方案的确定提供依据。郭健等[10]根据小波分析对风荷载作用下的斜拉索展开了损伤识别研究，并验证了该损伤识别方法的适用性。董晓马等[11]推导了柔度差矩阵并应用于斜拉索损伤识别，通过试验研究得出该方法能有效识别斜拉索损伤位置。上述研究可以看出，斜拉索损伤识别已取得较多有益的成果，但众多研究方法的实现过程较为复杂且稳定性较差，从而限制了其在工程上的使用。近年来，RBF神经网络由于结构简单、训练速度快，并且具有较高的动态仿真能力以及全局最优逼近等特点，在工程结构的损伤识别中得到了广泛的应用[12-15]。然而，作为高度冗余的非线性系统，斜拉桥拉索损伤具有自身特定的特点及变换规律，因此，基于RBF神经网络的斜拉索损伤识别还有待更细致的研究和探讨。

鉴于此，本文提出了基于RBF神经网络斜拉索损伤识别方法，阐述了其基本原理及实现方式，建立了斜拉索损伤识别分析框架，并以某实际工程斜拉桥的斜拉索为例探讨了该方法的适用性，以期为桥梁健康监测提供依据。

1 RBF神经网络原理及实现

1.1 RBF神经网络算法

RBF神经网络由Moody和Darken首次提出[16]，属于多层前馈神经网络。该神经网络模型共有三层，分别由输入层、隐含层和输出层组成，原理图如图1所示。其中输入层传递数据至隐含层，隐含层根据基函数对数据进行空间转换，并通过权值系数连接至输出层，最后通过输出层输出结果信息。

RBF神经网络由两个学习阶段组成：(1) 无导师学习阶段，通过径向基函数进行空间转换，并寻找基函数中心和方差；(2) 有导师学习阶段，通过权值系数连接隐含层和输出层，并不断调整以达到预期的精度目标。

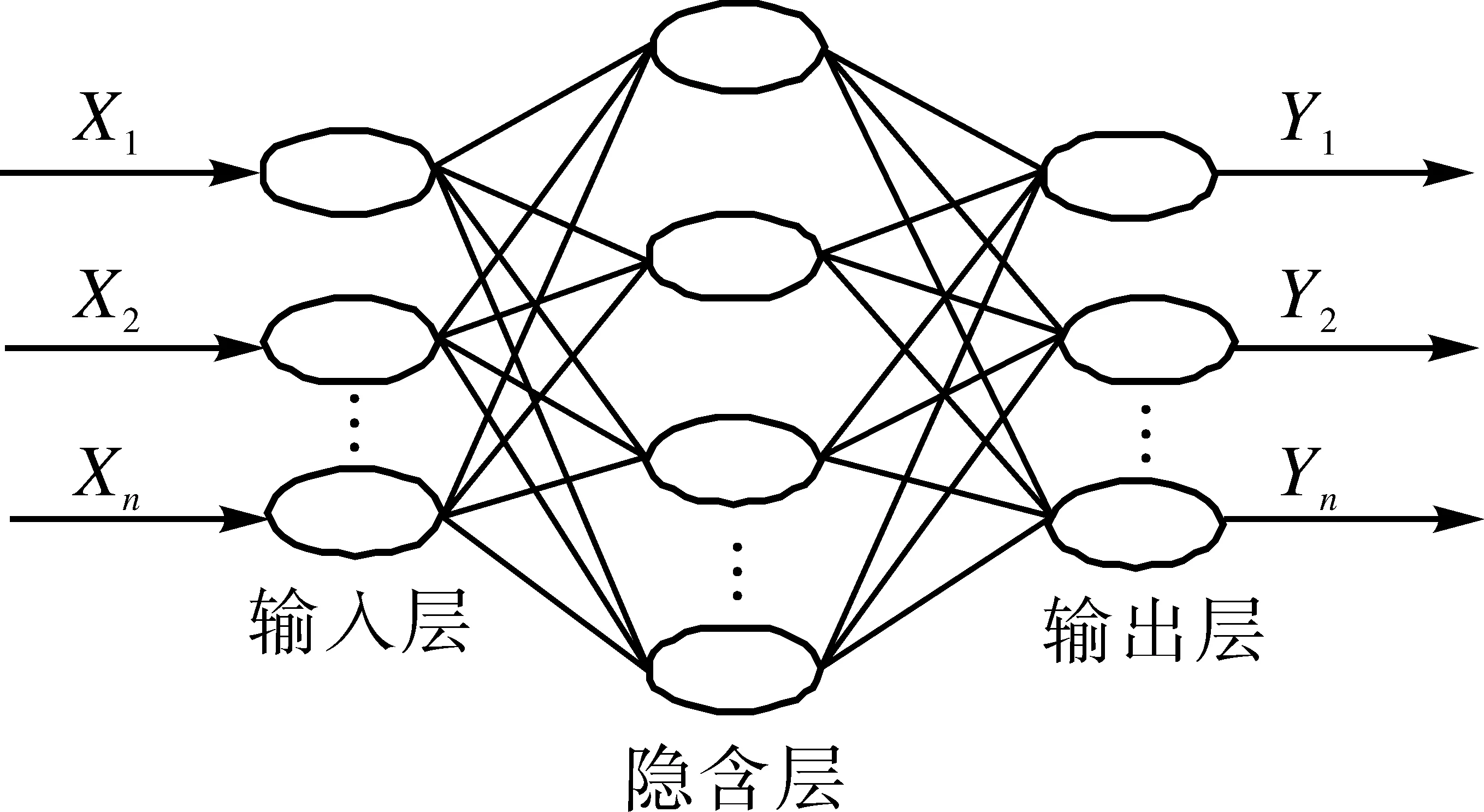
图1 RBF神经网络结构原理图

RBF神经网络的实现通常由基函数中心、方差和连接权值3个参数组成，对于基函数的选取，高斯函数是常用的激活函数[17]，表示为：

(1)

式中：‖xp-ci‖——欧式范数；

xp——第p个输入样本；

p——样本总数；

ci和σ——高斯函数的中心向量和方差。

通过基函数计算后，输出层函数表达为：

(2)

式中：wij——隐含层和输出层之间的权值系数；

h——隐含层节点数；

yj——对应第j个节点的实际输出结果。

1.2 基于Matlab的RBF神经网络实现过程

Matlab内置多种神经网络工具箱，通过调用这些工具箱，并调整相关参数，可得到满足精度的RBF神经网络模型，同时可大量节约编程工作。具体实现过程如下：

(1) 调用RBF神经网络进行网格训练，程序格式为：

[net，tr] =newrb(P，T，GOAL，SPEARD，MN，DF)

(3)

式中：net——RBF神经网络返回值；

tr——训练记录；

P和T——输入参数和输出参数，通常以矩阵形式表达；

GOAL——设定的目标误差，缺省时为0；

SPEARD——函数扩展速度；

MN——隐含层神经元最大值；

DF——迭代时频。

(2) 网络训练完成后，RBF模型调用格式为：

y=sim(net，x)

(4)

式中：net——训练完成的RBF模型；

x和y——输入样本和输出样本。

2 基于RBF的斜拉索损伤识别流程及实现步骤

基于RBF神经网络的斜拉索损伤识别，实际上是通过RBF神经网络构建样本输入和损伤指标的对应关系，经过网络训练获得满足精度的损伤指标预测模型。本文采用Matlab编制分析主程序，以斜拉桥有限元模型作为分析媒介，建立斜拉索损伤识别流程如图2所示，具体步骤如下：

步骤1：基于有限元软件，建立准确且合理的斜拉桥有限元分析模型。

步骤2：确定斜拉索损伤识别分析样本点，通过调用各样本点对应的斜拉索损伤指标数据，形成训练样本。

步骤3：根据训练样本，构造RBF神经网络模型，并设置输出目标以及允许的目标误差。对于斜拉索而言，输出目标通常设定为损伤位置和损伤程度。

步骤4：对RBF模型进行网络训练，直到误差达到设定误差后停止，此时得到满足精度要求的RBF神经网络模型。

步骤5：调用训练完成的RBF神经网络模型，对于不同测试数据可得到对应的预测值，以此进行斜拉索损伤识别。

图2 基于RBF神经网络的斜拉索损伤识别流程图

3 工程算例研究

3.1 斜拉桥有限元模型

本节以某实际工程斜拉桥斜拉索为例进行损失识别分析，以验证本文方法的适用性。该桥桥型为低塔斜拉桥，主跨跨度为220 m，两侧边跨长110 m。从左到右桥塔编号为1#和2#，斜拉索共40根，编号从左至右分别为A1～A20和B1～ B20，斜拉桥尺寸及编号示意图如图3所示。

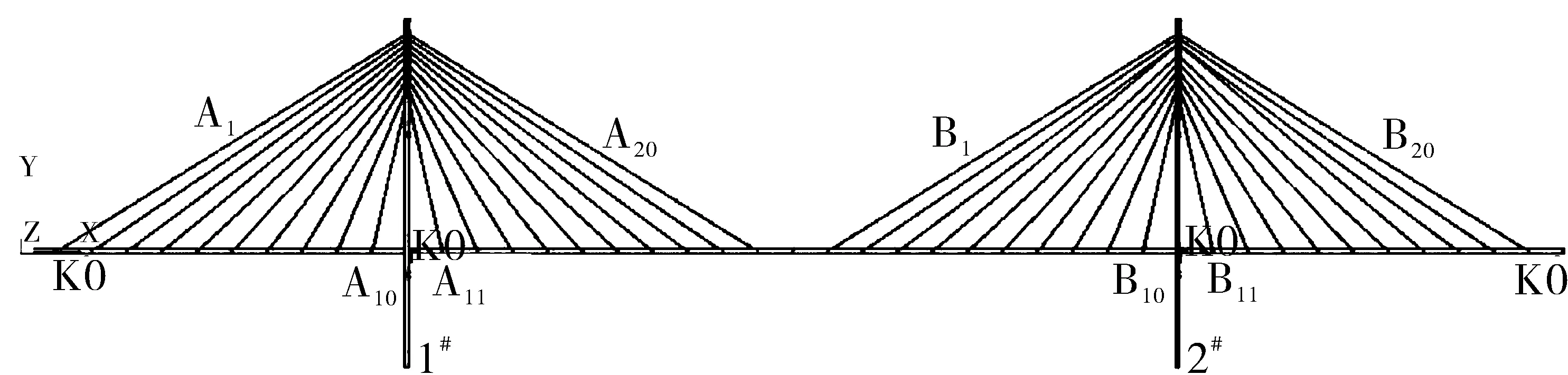
图3 斜拉桥尺寸示意图(m)

根据通用有限元软件ANSYS建立斜拉桥有限元分析模型，其中斜拉索采用杆单元模拟，单元类型为LINK10单元，桥塔、主梁和横向系梁均采用梁单元，单元类型为BEAM4单元，斜拉桥各组件材料参数如表1所示。对桥塔底部以及两侧横梁支座进行节点约束，在桥塔横梁和支座处设置弹簧约束。斜拉桥有限元模型如图4所示。

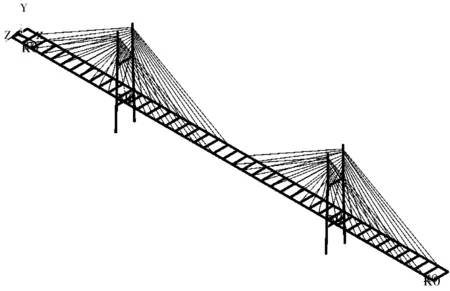
图4 斜拉桥有限元力学模型图

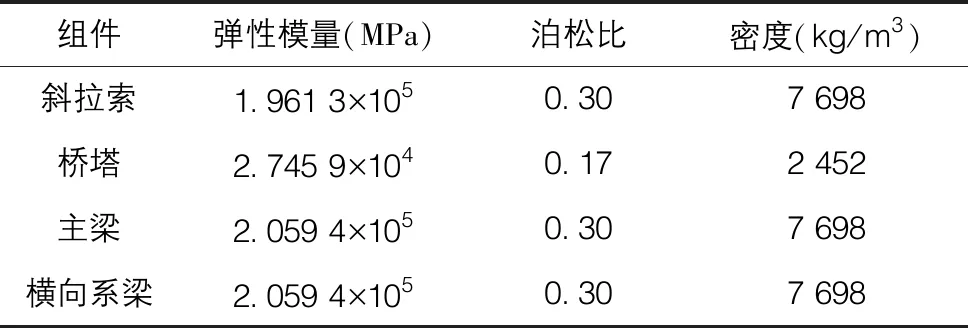
表1 斜拉桥各组件材料参数表

3.2 基于RBF神经网络的斜拉索损伤识别

3.2.1 主梁挠度增量

斜拉索损伤与主梁挠度增量一一对应，其中挠度增量表示为：

Δf=f-fg

(5)

式中：f——具体荷载工况作用下的主梁挠度；

fg——空载作用下，即只承受斜拉桥重力荷载下的主梁挠度值。

3.2.2 斜拉索损伤程度

斜拉索损伤程度通常采用面积模拟法[18]进行衡量，具体表示为：

(6)

式中：Y——斜拉索损伤程度，其区间为[0，1]，当Y=1时表示斜拉索处于完全损伤状态，当Y=0时表示斜拉索基本完好；

A和A′——初始状态和服役状态的截面面积。

3.2.3 RBF神经网络训练样本

以主梁挠度增量作为输入样本，斜拉索损伤位置和损伤程度作为输出样本，并结合现有分析数据可构建出RBF神经网络训练样本。基于一步识别法，输出样本可表示为：

Y=[Y1，Y2，…，Yn]

(7)

式中：Yi(i=1，2，…，n)——第i根斜拉索损伤程度；

n——斜拉索总根数。

3.2.4 误差评价指标

RBF神经网络训练时，需定义其停止准则，即当误差达到设定误差后表明该模型达到预期精度。对此，斜拉索损伤识别误差定义为：

(8)

式中：εi——第i根斜拉索损伤识别误差，设为0.005；

Yi′和Yi——第i根斜拉索实际损伤程度和RBF神经网络模型预测的损伤程度。

3.3 斜拉索损伤识别结果

综合上述分析，可对本算例斜拉桥拉索进行损伤识别分析。由于该斜拉桥左右对称，因此仅对A1～A20共计20根斜拉索进行分析。选取斜拉索损伤程度为30%、60%和90%三种工况，以对应测点的主梁挠度作为输入样本，斜拉索损伤程度作为输出样本，采用Matlab工具箱调用RBF模型进行网络训练。三种工况下的斜拉索损伤识别结果如图5所示。

根据测试样本，30%、60%和90%损伤工况下损伤的斜拉索编号分别为A6、A10和A14，对应的基于RBF神经网络损伤斜拉索编号为6、10和14(见图5)，能很好地识别斜拉索的损伤位置。

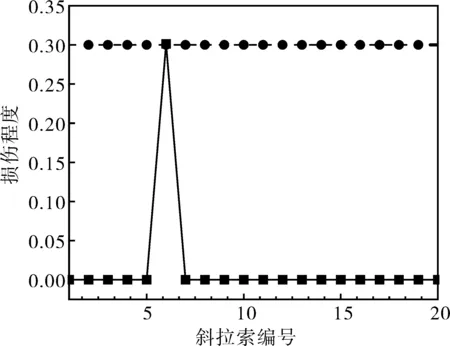
(a) 30%损伤工况

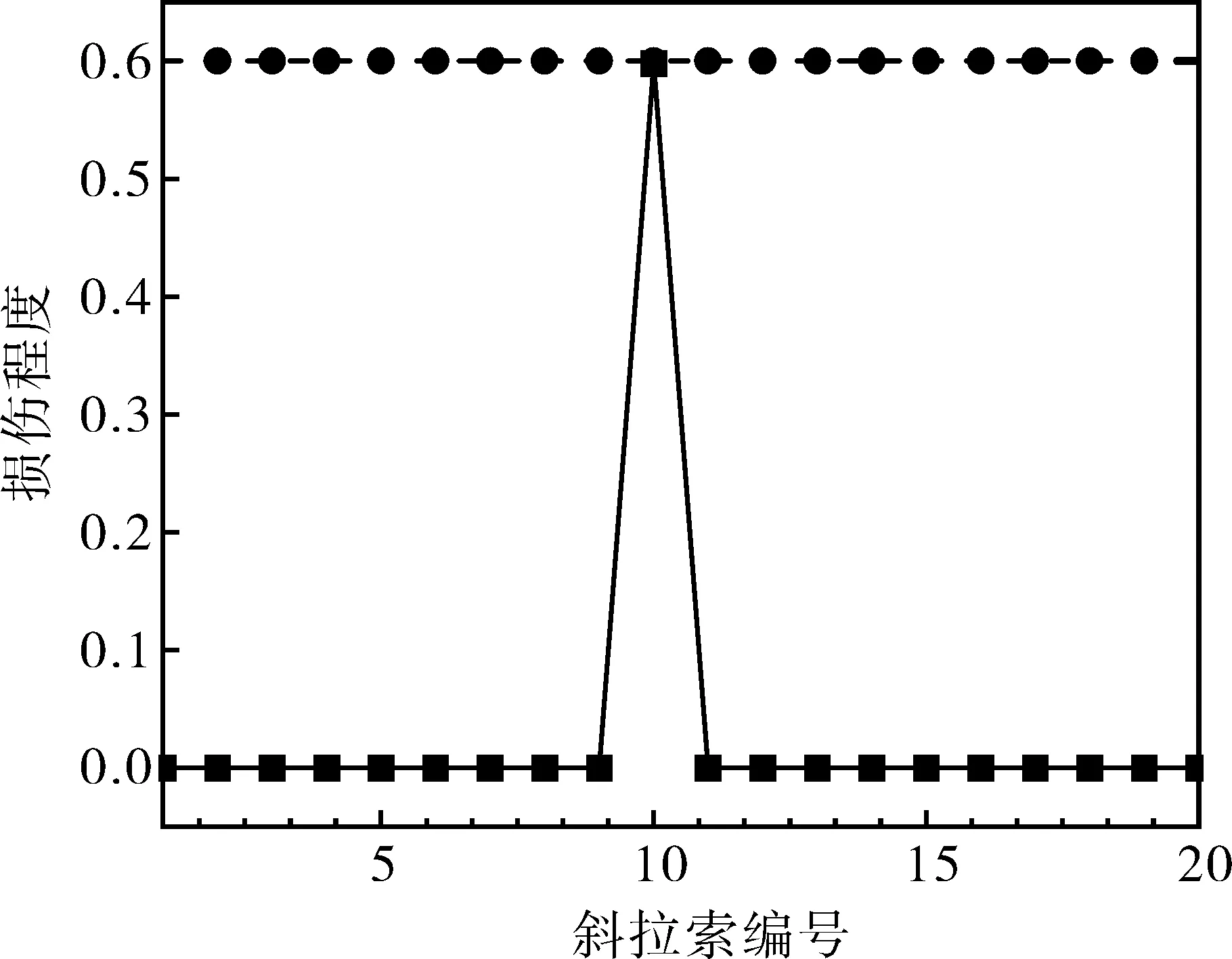
(b) 60%损伤工况

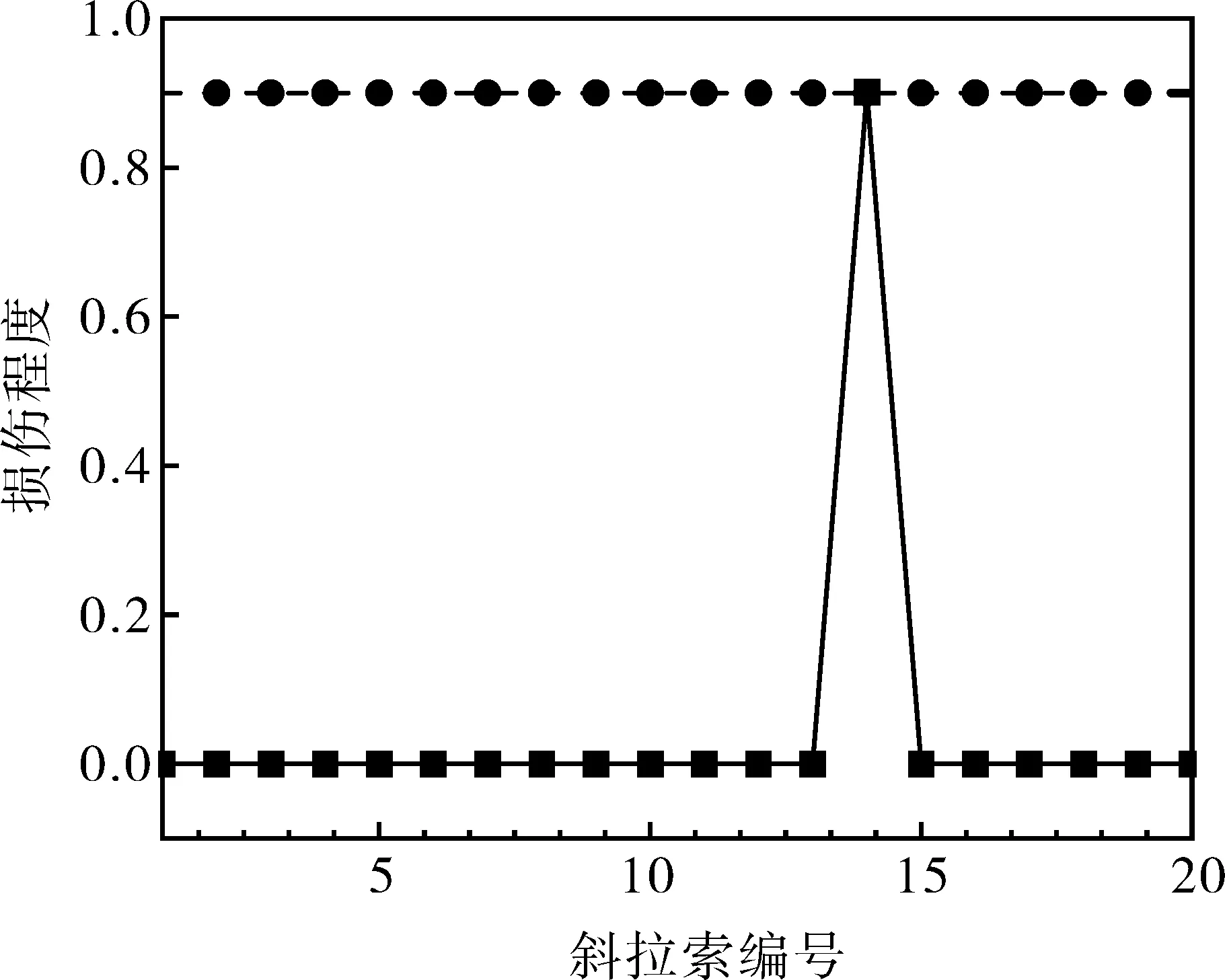
(c) 90%损伤工况

斜拉索损伤识别结果误差如表2所示，由表2可知，三种损伤工况条件下，通过RBF神经网络斜拉索损伤预测值分别为30.129%、59.790%和90.144%，其识别误差εi分别为0.004 3、0.003 5和0.001 6。根据前文定义，本文识别误差εi均<0.005，说明RBF神经网络模型能较好地适用于斜拉索的损伤识别研究中。

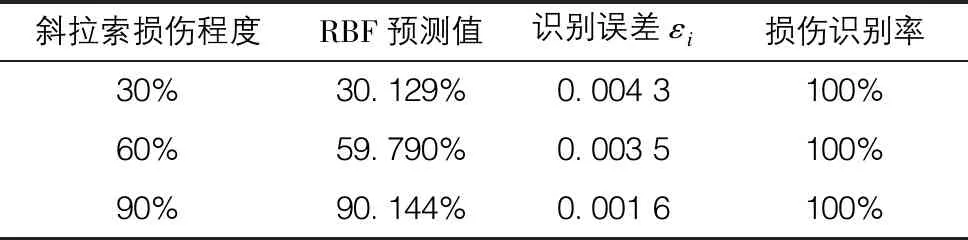
表2 斜拉索损伤识别误差表

4 结语

斜拉索的损伤状态关乎整个斜拉桥的使用性能，本文基于RBF神经网络模型，对斜拉索进行了损伤识别研究，并以实际工程斜拉桥为例验证了该方法的适用性。分析结果表明，基于RBF神经网络方法能很好地识别斜拉索损伤位置以及损伤程度。三种损伤工况下，损伤程度预测值相对误差分别为0.004 3、0.003 5和0.001 6，均处在较低的误差水平，可较为可靠地应用于斜拉索损伤识别。