一种基于SARIMA-LSTM模型的电网主机负载预测方法*

王 堃，郑 晨，张立中，陈志刚

(1．中南大学计算机学院，湖南 长沙 410083；2．国网宁夏电力有限信息通信公司，宁夏 银川 753000)

1 引言

随着人民生活水平的日益提高，电力企业的业务规模在不断增长，目前的系统运维水平已难以支撑多变的业务场景和问题。为了提高运维效率，许多研究人员开始致力于电力企业智能化运维研究[1]。时间序列的预测分析是其中重要的一环。目前，时间序列预测已经在工业环境中有了诸多经典的应用案例，如运用自回归AR(Auto Regressive)模型[2]、滑动平均MA(Moving Average)模型[3]或自回归滑动平均ARMA(Auto Regressive Moving Average)[4]模型进行负载预测。它融合了趋势性、季节性等时间序列结构的先验知识，对单一线性时间序列具有良好的预测性能。但是在现实场景中，内存等性能指标有着毛刺多、陡升陡降的特点。在预测这类复杂的时间序列数据方面,传统方法无法利用时间相关的特征，难以捕捉数据间的复杂模式。

近年来，在主机负载预测方面，国内外的研究人员已经开展了广泛的研究,并提出了一些行之有效的预测方案。文献[5]将ARIMA(Auto Regressive Integrated Moving Average)模型与分类回归树CART(Classification And Regression Tree)[6]相结合，采用了加权最小二乘法[7]和边界判定[8]进行优化，模型组合的方式弥补了自回归模型无法拟合非线性信息的缺陷，大大提高了预测精度。这些方法反映出自回归预测模型不断完善、融合和创新的过程。

然而，这些方法的一个关键问题是误差积累。在常见的统计学和机器学习方法中，大多数模型采用了滚动预测的策略。在预测过程中，将上一步的预测结果作为下一步预测模型的输入，这种误差的累积效应造成了数据的预测性能随着预测距离的增加而急剧下降。因此，在优化时间序列预测模型结构中，如何在减少误差积累的同时提高预测性能已成为当前研究的重要课题之一。文献[9]在多步预测的基础上，通过径向基函数RBF(Radial Basis Functoin)神经网络利用历史预测误差对未来时刻预测值进行修正，既解决了误差累积问题，也提高了预测准确性。文献[10]中的残差递归神经网络R2N2(Residual RNN)将传统的AR模型视为初始预测变量，并使用递归神经网络RNN(Recurrent Neural Network)估计残差，从其实验结论可以看出，对残差的补偿大大提高了时间序列预测的准确性。这2个方法为本文提供了研究思路。

在上述工作的基础上，本文提出了基于误差补偿的周期性ARIMA——SARIMA-LSTM(Seasonal Auto Regressive Integrated Moving Average-Long Short-Term Memory)预测模型。首先,建立周期性ARIMA模型SARIMA将时间序列进行周期性分解，然后分开预测。周期预测采用解离出的周期波动值，趋势预测使用ARIMA模型。对于SARIMA模型的预测误差，本文采取了误差自回归预测的方法分析历史误差与未来误差的关联性。最终周期分量、ARIMA趋势预测分量及误差补偿预测分量集成后得到预测结果。

2 方法与模型

对于给定的时间序列X={x1,x2,…,xn}，xi(1≤j≤n)表示n时刻时间序列的观测值。本文建立的误差补偿负载预测模型主要是以时间序列X为输入预测出n～n+v时刻数据值，并在一定程度上克服误差累积效应,其中v表示预测时间步长。具体技术原理将在2.1节和2.2节详细阐述。

2.1 SARIMA模型

ARIMA模型[11]是一种基于时间序列的预测方法,它由ARMA模型发展而来，用于解决实际生产环境中非平稳数据的预测问题[12],例如经济领域内的GDP和进出口额等数据[13]。ARIMA模型的主要思想是通过差分方法消去序列的局部水平或者趋势，再将差分后的序列应用到ARMA模型中，借此来实现非平稳时间序列的预测。ARIMA的建模公式如式(1)所示：

(1)

其中,yt代表时间序列X差分后在当前时刻t的值；μ表示常数值;p和q分别表示AR模型和MA模型的阶数;et表示误差值;γi表示自相关系数;θi表示相关系数[14]。

在此基础上的SARIMA模型考虑了周期性因素的影响，是指一种预测周期性时间序列的模型。为了消除时间序列中的周期变动因素，一般采用STL(Seasonal and Trend decomposition using Loess)分解等方法进行趋势解离、预测[15]。其变化周期用s表示。周期为s的乘积SARIMA模型建模公式如式(2)和式(3)所示:

(2)

(3)

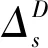
SARIMA的建模流程包括：数据预处理、周期性检验、平稳性检验、差分、BIC(Bayesian Information Criterion)准则[16]定阶、建模求参和残差检验。其中，周期性检验是SARIMA建模的重中之重，通过时序图观测法获得周期值s，如图1所示，横坐标为1天的24小时，多条线段代表不同日期内每天的负载值变化趋势。观察发现,9点到18点存在2个明显的波峰曲线，即存在明显周期变化趋势，周期值为12小时。本文采取ADF(Augmeted Dickey-Fuller)检验[17]，实验数据经过一阶差分就满足了平稳性要求。

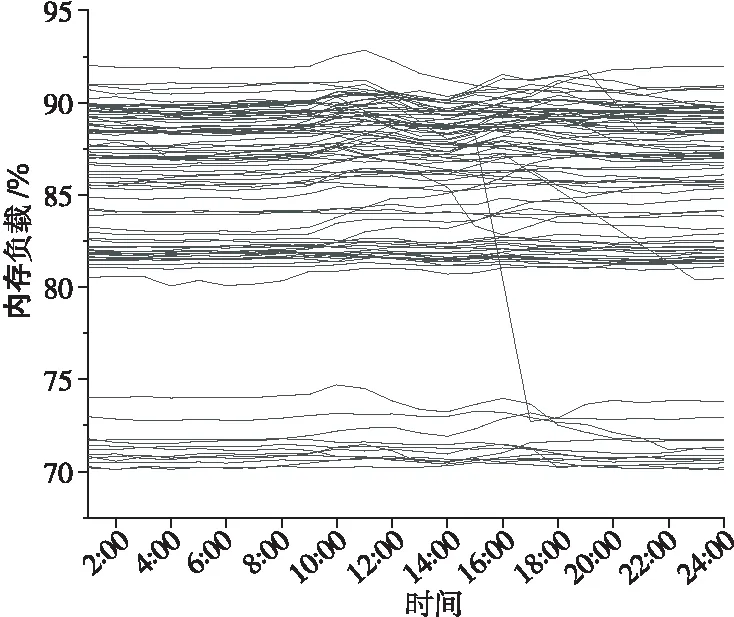
Figure 1 Daily periodogram of memory load time series图1 内存负载时间序列的日周期图

2.2 LSTM模型

LSTM网络[18]，又叫长短期记忆网络，是递归神经网络RNN的一种变体，主要是为了解决在训练RNN网络时存在的梯度爆炸和梯度消失问题。这些问题会造成特征输入RNN时,较早时间步的信息无法传递到较远的时间步中，使得整个网络可能遗漏掉极为重要的信息。

LSTM的核心在于它建立了一条贯穿所有时间步的信息流，通过门控机制控制每个时间步信息在信息流中的保留与删除。整体的模型结构如图2所示。LSTM在循环单元中采用了复杂的计算公式，其中最重要的核心结构被称为细胞状态(Cell State)。细胞状态是贯穿LSTM单元的信息流，在图2中用Ct-1到Ct的直线箭头流表示。

Figure 2 Structure of LSTM model图2 LSTM模型结构

下面详细介绍LSTM单元的具体结构：

(1)遗忘门(Forget Gate)。

在LSTM单元中，首先决定细胞要遗忘哪些信息。将上一单元的隐藏状态ht-1和当前单元的输入序列xt输入遗忘门，经过sigmoid函数后生成输出向量ft,其分量取值在[0,1]。向量中分量的值为0时，表示Ct-1的信息完全不保留；为1时，表示Ct-1的信息完全保留,具体如式(4)所示：

ft=σ(Wf·[ht-1,xt]+bf)

(4)

其中,σ(·)为神经网络中的sigmoid激活函数，Wf表示权重参数。

(2)输入门(Input Gate)。

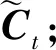
(5)

it=σ(Wi·[ht-1,xt]+bi)

(6)

其中,tanh表示神经网络中的激活函数，WC和Wi表示权重参数，bC和bi表示偏置参数。

(3)更新门(Update Gate)。

经过遗忘门和输入门后，确定了丢弃和更新的信息。接着对细胞状态进行更新操作，得到Ct,具体如式(7)所示：

(7)

(4)输出门(Output Gate)。

更新细胞状态后，首先通过sigmoid函数处理输入的ht-1和xt，得到判断条件向量ot。然后，使细胞状态Ct经过tanh函数，得到每个分量取值为[-1,1]的向量值，该向量与ot相乘，得到LSTM单元的输出ht，具体如式(8)和式(9)所示：

ot=σ(Wo[ht-1,xt]+bo)

(8)

ht=ot*tanh(Ct)

(9)

其中，Wo表示权重系数，bo表示偏置系数。

综上所述，LSTM通过其内部门控机制和模型循环结构，实现了具有长短期记忆的时间序列数据处理模型。

2.3 SARIMA-LSTM模型

ARIMA模型被广泛应用于设备状态预测中，通过差分方法处理非平稳数据，挖掘出历史数据与预测数据的函数关系，实现数据预测并推测出置信区间。但是，传统的ARIMA在进行多步预测时，存在误差累积现象，难以满足预测精度的要求。为此，本文提出了SARIMA-LSTM模型，首先，通过STL分解建立SARIMA模型;然后,对其进行误差补偿分析，利用误差数据训练LSTM神经网络；训练完成后，利用现有历史误差数据预测未来误差；最后，结合SARIMA模型的预测值和LSTM的误差补偿值得到指标值未来12小时的预测值。

SARIMA-LSTM模型的建模流程如图3所示。首先，进行数据预处理，删除无关指标项后，取内存值每小时的均值作为该小时的指标值；然后，依据数据缺失状况，采用K最近邻插值法对数据进行补全；最后，输出SARIMA-LSTM模型预测结果。

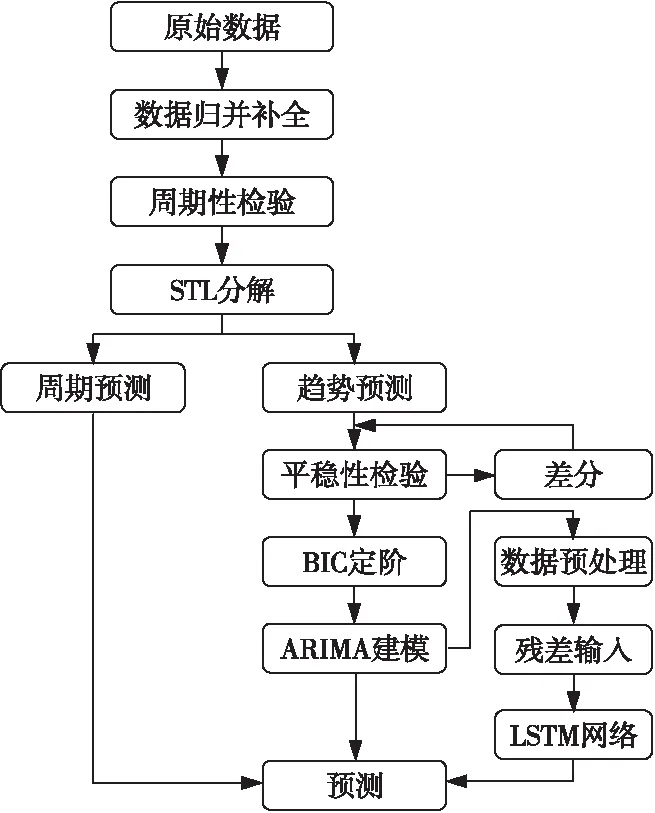
Figure 3 Flow chart of SARIMA-LSTM modeling图3 SARIMA-LSTM建模流程图

2.4 模型评价指标

本文的评价指标采用相对均方误差RMSE(Root Mean Square Error)[19]和决定系数R2[20]。均方根误差RMSE对一组预测结果中的极大或极小误差比较敏感，它可以反映出预测的精密度和整体偏差大小。RMSE值越小，代表模型预测越准确。决定系数是用来衡量预测结果与真实样本之间的相似程度，正常值处于[0,1]，结果越接近于1说明预测模型的拟合效果越好。2个指标的计算公式分别如式(10)和式(11)所示：

(10)

(11)

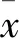
3 实验与分析

本文将提出的SARIMA-LSTM模型应用于宁夏电力公司财务应用服务器的内存负载数据，采样间隔为5 min。本文的所有方法基于Python3.8实现，实验环境采用Windows10，AMD Ryzen 5 3550H with Radeon Vega Mobile Gfx 2.10 GHz，16 GB内存。神经网络使用PyTorch 1.4.0+cu92实现。

3.1 实验数据与参数

建模过程的数据信息如表1所示。

首先对实验数据进行周期性检验，根据周期情况进行STL分解，得到周期分量和趋势分量(包含随机部分)。周期分量作为周期预测部分加入模型预测值中。在趋势分量上，建立ARIMA模型预测趋势部分，通过StateModels方法得到历史数据预测误差。在其基础上，建立LSTM训练集及测试集。输入LSTM模型进行训练。最后将周期预测值、趋势预测值和误差预测值累加在一起，得到多步预测结果。最终的预测公式如式(12)所示：

Table 1 Information of modeling data表1 建模数据信息

(12)

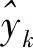
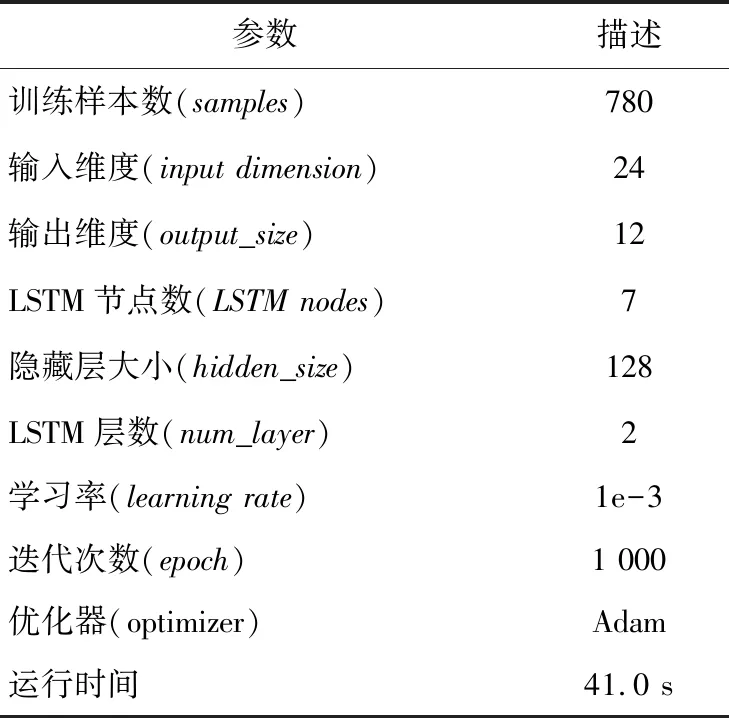
Table 2 Parameters of LSTM model表2 LSTM模型参数

3.2 数据预处理

图4所示是2020年3月1日内存负载的波动变化图。图4a采样间隔为5 min，数据上下波动剧烈;图4b时间间隔为1 h，数值取每小时均值，数据波动平稳。对比可以发现,数据经过归并后，消除了影响预测的数据抖动，又保留了大体趋势。

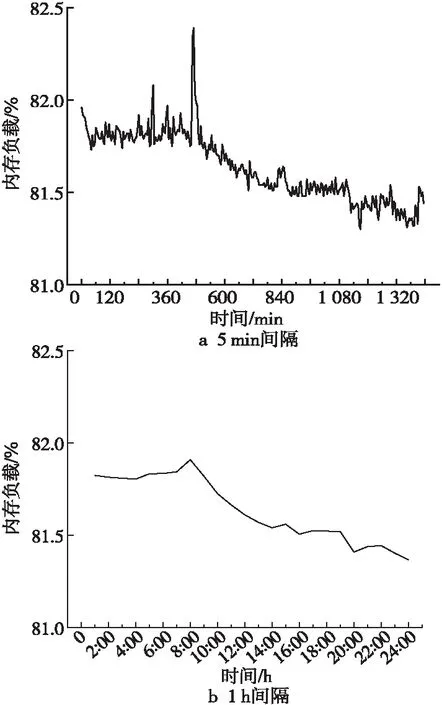
Figure 4 Memory load time series of 5-minute and 1-hour intervals图4 5 min间隔和1 h间隔内存负载时间序列

3.3 实验及结果分析

使用SARIMA-LSTM模型对预处理后的内存负载时间序列进行训练和预测，预测误差绝对值变化如图5所示。

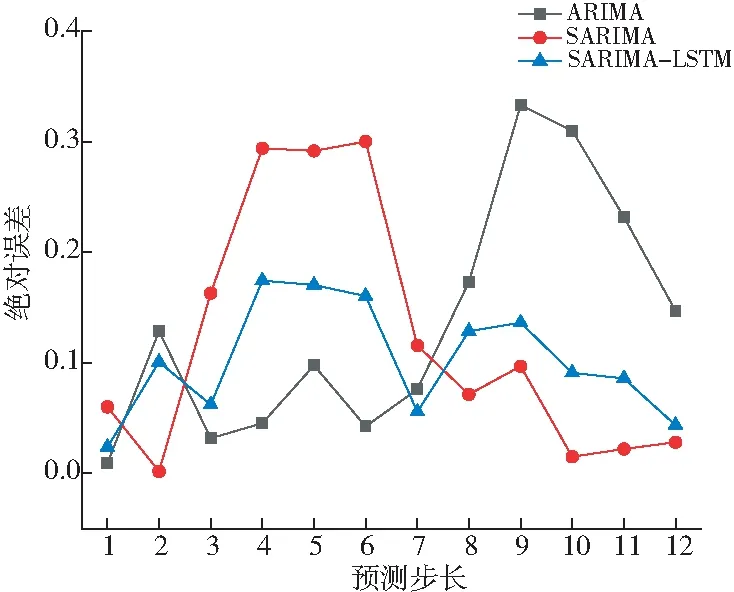
Figure 5 Variation of absolute prediction error图5 绝对预测误差变化

从图5可以发现，ARIMA在进行前1～6步预测时，误差较小，在6～12步时误差值急剧上升，绝对误差最大值为0.332 97，其预测效果需进一步提高。对ARIMA进行周期补偿后，SARIMA模型前半段误差增大，后半段的误差显著减小，整体多步预测效果相对于ARIMA提升不大。因此得出结论:SARIMA可以有效减少误差累积，但周期变化会影响短期预测精度。而从图像上看，SARIMA-LSTM模型前12步的绝对误差值都小于0.2，整体预测性能高于其他模型。由此可见，SARIMA-LSTM能够较好地权衡长期和短期预测效果，使得一段时间内的整体预测结果有显著提升。

如表3所示，本文采用不同评价指标综合比较不同模型的预测性能。在RMSE值上，ARIMA模型、SARIMA模型和SARIMA-LSTM模型的RMSE值分别为0.170 7,0.162 0和0.117 6，ARIMA的多步预测误差最大，相比之下SARIMA-LSTM误差下降了0.0531，这说明SARIMA-LSTM模型的误差补偿方法显著提升了模型的预测效果。在R2值上，SARIMA-LSTM模型的R2值为0.564 6，在3种预测模型中数值最接近1，这反映出SARIMA-LSTM模型的拟合效果最好，优于其他模型。

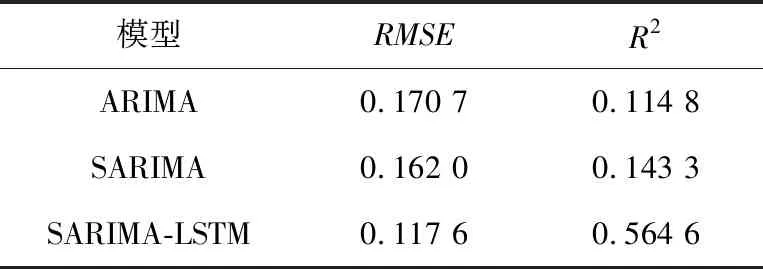
Table 3 Comparison of indicators of different models

除了模型预测性能的比较以外，本文还利用SARIMA-LSTM模型的预测结果生成了内存负载的动态阈值区间。如图6所示，本文利用置信理论生成阴影区间，表示未来这一预测时间段的指标值有95%的可能性处于该区域内。首先，从真实值和预测值之间的对比效果来看，本文模型可以准确地预测内存负载在白天业务高峰期7点～18点的波动变化。其次，将95%置信区间作为阈值区间后，可以发现正常的指标值波动处于阈值区间内时不会触发报警。而实际内存负载超出了该区间，说明发生了概率为5%的内存异常事件，系统通知运维人员进行设备运行状态检查。这种利用服务器内存历史数据预测并估算设备运行指标动态阈值的方法，可以提高设备故障的预知能力，充分提升运维监控和故障抢修工作的主动性，提高了运维效率。

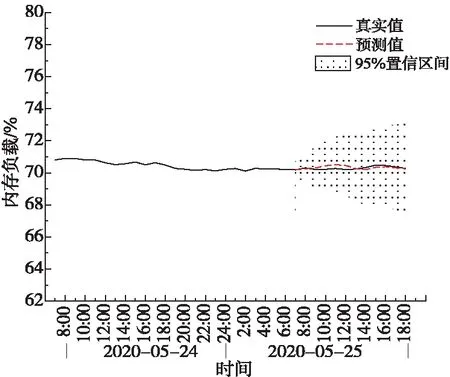
Figure 6 Prediction results of SARIMA-LSTM图6 SARIMA-LSTM预测结果

4 结束语

本文借鉴了时间序列预测方向应用广泛的预测模型以及误差补偿的前沿算法技术，提出了一种基于LSTM误差补偿的电网主机负载预测模型——SARIMA-LSTM模型。在综合分析了电网主机负载数据的波动性和周期性后，建立SARIMA模型对时间序列趋势、周期进行分开预测，再利用 LSTM误差补偿模型对SARIMA预测误差进行自回归分析。实验数据中，以内存负载数据为例，验证了本文所提出的模型在电网运维场景中的准确性和有效性。本文的未来研究工作如下：

(1)预测指标项。值得注意的是，本文的预测指标项为主机内存负载数据。业界常用的设备运行状态指标还有CPU负载数据。下一步可以考虑进行多元时间序列预测，提高预测模型的稳定性和准确性。

(2)实时性。智能电网建立在集成、高速的双向网络上，需要运维人员能够及时地发现问题甚至是预测问题。所以，需要在保证预测精度的情况下，降低预测模型的计算消耗，提高运算速度。

(3)自动化。电力运维系统逐步向高集成化、高智能化发展，先进的自动化系统可以实时调取历史资料信息，建立信息分析平台，防范未知风险。未来，先进的设备监控技术、信息决策技术、智能调度技术将在智能电网领域发挥巨大作用。