基于某核电汽轮发电机组分析轴系中心偏差对振动的影响

郭孟磊，周功林，张立军，周党锋

（1.中广核核电运营公司有限公司，广州 深圳 518000；2.辽宁红沿河核电有限公司，辽宁 大连 116000）

0 引言

轴系中心偏差标准的限定，无论是制造厂还是检修技术规范要求均较严苛。一直以来，历史在汽轮发电机组的安装、检修及振动故障诊断中，均将轴系中心偏差作为激起轴系振动最重要的外部激振力。施工现场一般将转子两联轴器断开状态下其轴向中心线上下、左右偏差称为“圆周”偏差，两相邻联轴器端面上下、左右平面间距偏差称为“张口”偏差，两者统称为“中心偏差”。某些资料及技术书籍又将前者称为平行不对中，后者称为角度不对中。为了不混淆概念并贴近现场应用，本文中“中心”的概念遵照上述施工现场的叫法，将联轴器连接后的两转子轴向中心线偏差称为“同心度”（某些资料称作“同轴度”）。

1 建模思路

本文建立转子模型，采用有限元分别计算：①0.10 mm“张口”偏差产生弯矩（将消除0.10 mm张口所产生的弯矩施加到模型上）对振动的影响值； ②0.10 mm“张口”偏差产生弯矩叠加不均匀摩擦力对振动的影响值；③无张口，但轴系存在0.10 mm同心度偏差对振动的影响值；④无张口，但存在单转子重力10%的不平衡力对振动的影响值（相当于在某核电站低压转子对轮上加重1 000 g）。分别计算几种状态对轴系振动影响的量值并进行对比分析。

轴系模型如图1所示。

图1 轴系模型

2 基于转子模型的有限元分析

有限元分析条件及假设：①轴系运转角速度为314 rad/s；②摩擦系数选取0.15；③轴系圆周转矩无偏差；④转子一端完全限制轴向位移，模拟机组推力轴承；⑤轴承完全刚性；⑥对轮、转轴、螺栓孔节圆完全同心；⑦转子材质完全均匀。

下面分别利用有限元分析上述几种类型对振动的影响值。有限元分析网格基本信息为实体网格类型、基于曲率的网格器、节点总数为146 818、单元总数为94 956。

分别利用有限元计算上述4种状态对轴系振动的影响。

2.1 0.10 mm“张口”偏差产生弯矩对振动影响值的有限元计算条件

消除0.10 mm张口，需要在两对轮同一方向径向分别施加5 000 N的力在模型上而产生的弯矩。

2.2 0.10 mm“张口”偏差产生弯矩叠加不均匀摩擦力对振动影响值的计算条件

考虑两种因素的影响相互叠加，部分螺栓紧力用于消除张口带来的阻力，叠加对轮两端产生弯矩对轴系振动的影响。螺栓紧力分布如图2所示。

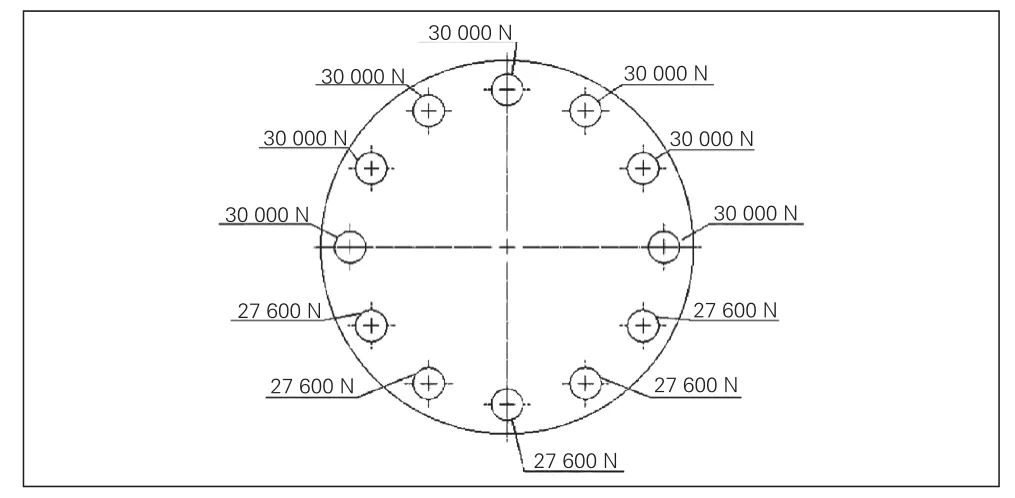
图2 消除0.10 mm“张口”偏差致使螺栓在端面产生不均匀紧力分布

2.3 无张口，但存在0.10 mm同心度偏差对振动影响值的有限元计算条件

去除“2.1、2.2”章节中施加的5 000 N的力，以及螺栓紧力的不均匀分布。

2.4 无张口，但存在一根转子重力10%的不平衡力对振动影响的计算条件

两对轮不存在张口，但其中一对轮面存在10%转子重力（单根转子）的不平衡力，本模型中单根转子重7 089 kg，对轮直径为800 mm，其10%的重力的不平衡质量：

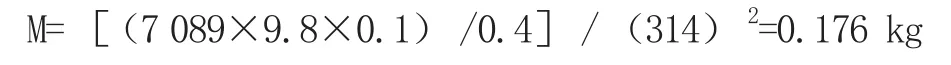
相当于在某核电低压转子对轮加重：

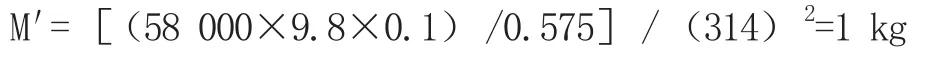
将上述4种状态的条件分别代入有限元计算，分析结果见表1。

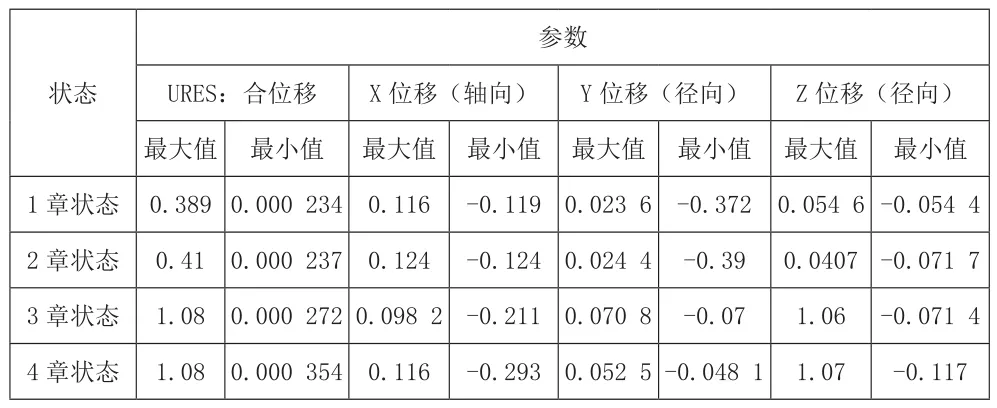
表1 有限元计算结果 （单位：mm）

由表1中数据可得出3.1节/3.2节/3.3节/3.4节中的最大径向位移（轴系径向振动值）之比分别为|-0.372|/|-0.39|/ 1.06 /1.07=1/1.05/2.85/2.88。

2.5 各状态对比分析

（1）“张口”偏差对振动的影响值随“张口”的增加而增加，但量值较小，按照某核电低压转子对轮加重对低压转子两侧轴振影响值60～70 μm/kg计算[1]，0.10 mm张口对振动影响值为21～24 μm，叠加圆周摩擦力不均匀也仅造成 22～25 μm的振动值影响。由此可见，“中心偏差”对振动幅值的影响量值较小。

（2）“不平衡”和“同心度偏差”是影响轴系振动的主要因素，0.10 mm同心度偏差与对轮上加重10%转子重力的不平衡量产生的振动幅值相当，按照某核电低压转子对轮加重响应值计算，0.10 mm同心度偏差将造成59～69 μm的振动值影响。

（3）以上为单一因素对轴系振动的影响值，但实际中上述各因素都会不同程度地存在并且相互耦合，因为上述各值均为矢量，所以其合力对轴系振动影响最终由各矢量同向或者反向决定。

（4）由以上分析结果可以看出，只要加工制造精度得以保证，对轮断开状态下的“中心偏差”对轴系振动的影响值相对较小，例如某核电某次大修汽发对轮张口达0.20 mm之多，但机组满功率及空载轴振均保持在50 μm以下的较低水平。

通过以上的分析可知，“中心偏差”并非是引起轴系振动的主要激振力，但不可忽略的是“中心偏差”带来对轴系的衍生影响而非对轴系振动的直接影响。

3 “中心偏差”常见故障模式及振动特征

3.1 轴系中产生除1倍频以外的2倍频及其他谐波分量

汽轮机运行中主要由摩擦力传递转矩，在联轴器圆周内所有螺栓施加紧力一样的情况下，“张口偏差”则造成联轴器圆周面形成不对称的转矩传递，转轴圆周因受力不均匀产生径向1倍频振动。

柱销螺栓连接并加工止口结构的联轴器，圆周偏差将限制在螺栓与螺栓孔配合及止口之间0.02～0.04 mm的配合精度上，“圆周偏差”在螺栓穿入后可忽略，但会对转子产生一定“弯矩”起到“曲轴”作用。

以上因“中心偏差”对两端转子弯矩及圆周不均匀转矩传递作用，除产生类似于质量不平衡的 1倍频振动外，还会因转子径向承受交替作用力而产生2倍频振动分量。

假设不对称的转矩传递中M1>M2，随转子旋转始终有F1-F2的力作用在联轴器，类似于在联轴器端面施加了一个（F1-F2）×g的重量，使转轴产生一个类似于质量不平衡的1倍频振动。

因中心偏差对转子的弯矩作用，始终存在一个作用于联轴器一个不变方向的力F1′，当F1′与不平衡质量同方向时振幅A1最大，转子旋转180°。则F1′与不平衡质量变为反方向，振幅A2最小。如此转子每旋转一周，A1和A2交替变化一次，产生2倍频振动分量，轴心轨迹可变现为较高椭圆度的香蕉形。

3.2 轴系中各轴承不均匀载荷分配造成过载或低频涡动

圆周偏差会造成联轴器两端轴承一侧载荷加重一侧减轻，重载一侧因油膜厚度较小，致使油内产生较大剪切力，轴承载荷区域的油温升高，并将热量传递至轴承的巴氏合金层中，巴氏合金层温度升高，其强度呈指数降低，一般的巴氏合金层当温度达125 ℃时即可发生蠕变，过大的载荷易使轴承巴氏合金层产生熔融、碾压、材料迁移等故障。

轻载一侧则会降低偏心率，增加流体平均速度比，失稳转速值降低，促使在外界扰动下诱发半速涡动甚至油膜振荡的概率增大。其形成机理由转子运动方程可知[2]：

式（1）中：k为支撑系统弹簧刚度；r为转子偏心（转子轴心相对于轴承中心的偏移值）；m为产生外部扰动项的质量（不平衡质量）；D为流体阻尼常数；λ为流体周向平均速度比；ω为外部扰动力（不平衡）旋转角速度；Ω为转子旋转角速度；M为转子质量；为转子运动速度；为转子运动加速度。

式（1）中，切向刚度项“iDλΩ”是促使转子沿旋转切向方向产生涡动的主要因素，是转子转速Ω和流体周向平均速度比λ的函数,当轴承过于轻载造成转子偏心率降低时，随着转子远离轴承内壁，λ值快速增加，切向力促使转子沿旋转方向产生空间涡动。受λ值影响，涡动频率一般≤1/2转子转速频率。

3.3 因中心偏差造成的轴承轻载将降低轴系失稳阈值

式（2）中，λ增大，Ω失稳值势必会降低，若失稳阈值Ω失稳降低至工作转速以下，则在外界扰动下转子轨迹发散而最终发展成油膜振荡。油膜振荡发生时转子承受可引起轴系破坏的交变应力。过大的中心偏差造成一侧轴承轻载是促使油膜振荡形成因素之一。

3.4 过大的中心偏差可使转子振型节点位移，造成对转子振型的误判

通过振动数据判断转子振型是现场实施平衡，采取合理动平衡加重形式的必要条件，但在现场实施中却常见通过采集到的转子两端轴振数据分析振型，由模态平衡法[3]实施加重却失败的例子。比如，采集到的转子两端轴振数据分析为较明显的二阶不平衡形式，但实施二阶平衡配重形式后计算影响系数，却发现影响系数反相分量非常小，而使动平衡无法继续实施。

一般对于一阶振型，因转速较低，尚未受其他振型的影响，振型单一容易判断。目前，机组大多运行在一阶与二阶之间，部分发电机转子运行在二阶以上三阶以下。工作转速受一阶残余振型及二阶早期振型或二阶残余振型及三阶早期振型的共同作用，所以对于振型的判断相对困难，并且因“中心偏差”外力作用导致的振型节点位移，以及因轴承动力学刚度不同，导致两端轴振滞后角分散所造成的相位差别，则有可能使振动探头检测到的相位角差别较大，非常容易误判振型。

3.5 运行中产生的中心偏差或检修中不合理的调整方式将衍生复杂振动

很多机组运行一个周期后，往往因基础的不均匀沉降、缸体膨胀、轴承座温度变化、管道牵引力等复杂因素，造成停机解体复测中心数据与原始检修中心数据偏差非常大，落地式轴承受基础不均匀沉降影响明显，坐落在排汽缸的轴承座受排汽缸温度和真空度影响明显，轴系中各转子中心随运行时间及冷热态、运行工况的变化而变化，使轴系中各轴承载荷重新分配，并进一步影响轴系中各转子的动力学行为。所以，针对不同机组应收集总结各自轴系在不同状态下的变化规律，找到合理的冷热态及各工况下轴系中心变化量，找到规律并修正，在转子冷态下找轴系中心时预留偏差值。

对于发电机，常因轴系中心调整忽略了发电机本身结构参数而导致电磁激振等复杂振动问题。例如，某机组在解体后测量汽轮机、发电机对轮中心，发现下张口0.15 mm，检修中未认真分析导致该张口的原因为基础不均匀沉降，并且未检查该状态下的发电机气隙值，单纯为了调整中心而降低发电机后轴承坐标高，使发电机励端气隙偏差进一步增大，中心偏差虽然调整到了标准范围内，启机后却带来复杂的振动，随励磁电流的增加表现出较大的2倍频及丰富的高频振动成分增长[4]，只能临时通过动平衡手段降低振动基础值，维持运行至下轮大修处理发电机气隙不均匀问题。

4 结语

经有限元计算分析造成轴系振动主要的激振力来源于质量不平衡及轴系连接“同心度”偏差，轴系“中心偏差”本身对振动的直接影响比较小，其曲轴作用及不均匀的转矩传递将产生除1倍频振动之外的2倍频及其他谐波分量。

应重视“中心偏差”对轴系的衍生影响如：载荷不均匀分配使高载荷轴承瓦温升高，低载荷轴承激发低频涡动甚至于油膜振荡。过大的中心偏差使转子振型节点迁移，对转子振型误判。

中心偏差使轻载轴承发生失稳故障的概率增加，经分析半速涡动故障在具备油膜形成条件下的任意转速都可能发生，油膜振荡发生的基本条件一定是工作转速大于2倍的一阶临界转速。