地下连续墙竖向承载研究

祝迎建

（原子高科股份有限公司，北京 102400）

0 引言

地下连续墙开挖技术起源于欧洲，它是根据打井和石油钻井使用泥浆和水下浇注混凝土的方法而发展起来的［1］。在我国，闭合地连墙大多作为支护结构，而完全作为承重结构，在我国很少使用在桥梁领域中。作为整体刚度大、强度高的基础结构，适用于对不均匀沉降较为重要的工程中，例如大跨度桥梁的桥墩。根据文献［2］统计，日本是地连墙作为竖向承重基础使用最为频繁的国家，但由于其国多遇地震，故偏重基础在水平地震荷载下的研究，对竖向的承载力深入研究较为稀少，其他国家对于此基础的研究寥寥无几。而我国的学者主要通过室内模型试验，现场原位试验等对简单截面的闭合地连墙基础进行了研究，而对于形状较为复杂截面的地连墙基础的研究则非常少。由于特殊的几何构造，形状较为复杂截面的地连墙基础内部存在诸多的墙芯，在承载过程中，墙体、土体的互相作用是主要研究点。本文应用数值模拟的方法，研究了复杂截面的地连墙各分力的发挥过程，并总结了承载力的计算公式。

1 模型建立

采用有限元软件 ABAQUS 对复杂截面的地连墙进行建模处理，基础的截面尺寸如图 1～图 3 所示，建模参数如表 1 所示。

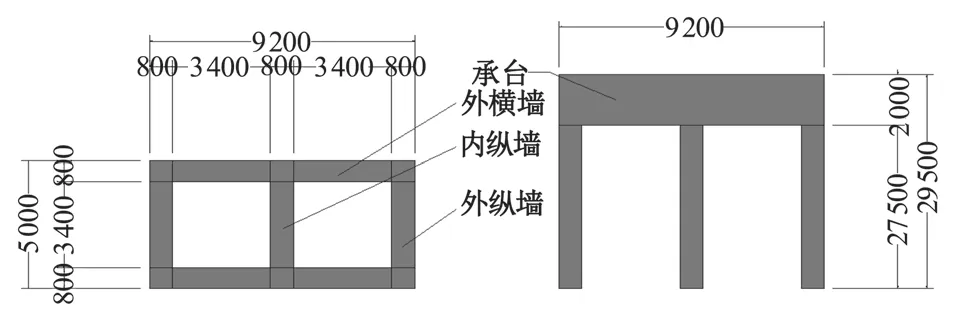
图1 两室墙截面尺寸示意图（单位：mm）

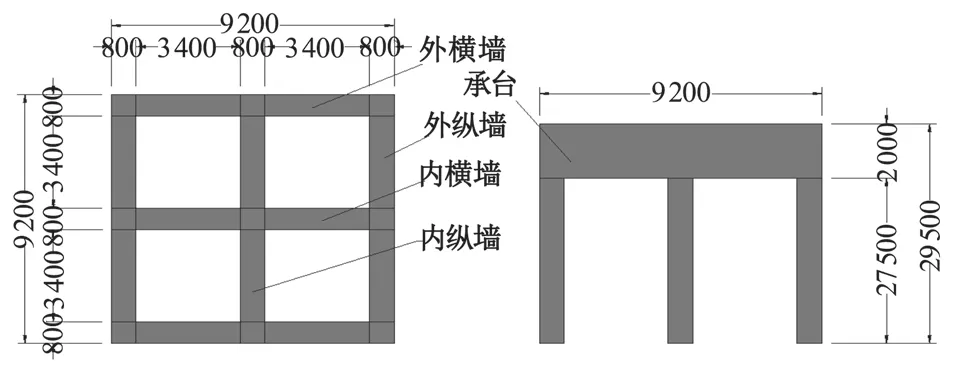
图2 四室墙截面尺寸示意图（单位：mm）

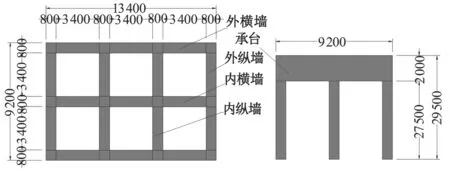
图3 六室墙截面尺寸示意图（单位：mm）

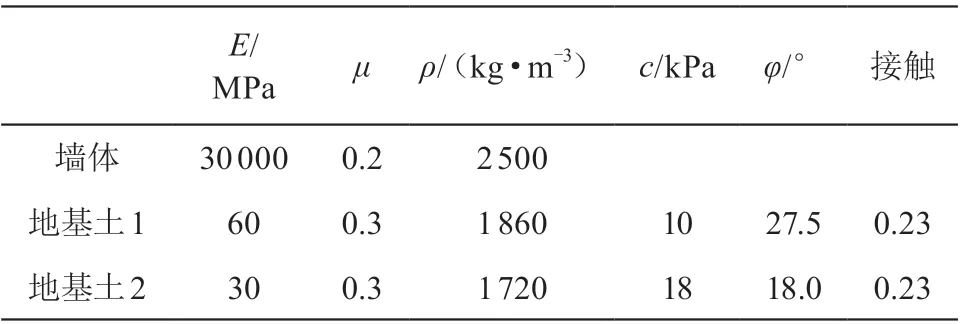
表1 建模参数

对地连墙施加竖向外荷载，荷载共分为 10 级，每次加载量为最大施加荷载的 10 %，逐次累加。地连墙基础的沉降曲线如图 4 所示。

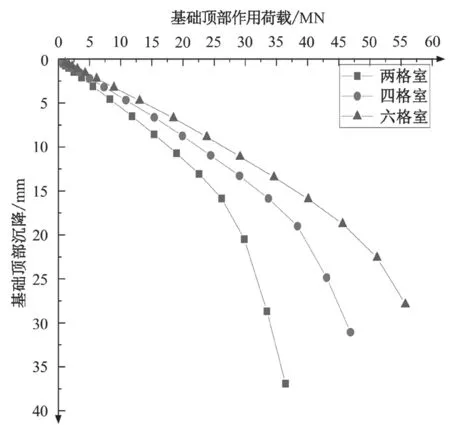
图4 三类基础的荷载 Q-沉降 s 曲线

图 4 中荷载沉降曲线有 2 段组成。①弹性阶段的直线段，沉降与施加于顶部的荷载成正线性关系。②曲线陡降段，当基础达到极限承载状态时，其沉降开始急剧增加，曲线斜率越来越大。由于缺少相关此类基础的相关规范，考虑到地连墙的承载形式与桩基类似，故采用常用的桩基极限承载力确定的方法判断复杂截面地连墙的极限承载力。将作用荷载Q-沉降s曲线用 LgQ-s曲线表示，曲线变为直线时的转折点，该点即为极限承载力。如图 5 所示，三类基础的竖向极限承载力分别为 29 MN、43 MN 和 55 MN。三类基础的内部墙芯的大小是相同的，其竖向极限承载力并非不会随墙芯数量的增加，呈线性正相关，因为墙芯数量越多，内墙在端部会产生应力干扰效应，抑制复杂截面的地连墙的端阻力与内侧摩阻力的发挥。

2 端阻力

在竖向极限荷载下，墙基础端部竖向应力差异较小（见表2），墙芯顶部的承台土阻力远远小于端阻力，对于竖向承载力发挥着较小的作用，可以略去。图 6、图 7 是墙基础在其自身的竖向荷载下，端部的竖向应力云图，从云图中可以看出：复杂截面的地连墙基础达到极限承载状态时，外墙的端阻力与内墙的端阻力的分布存在明显的差异，外墙大于内墙的阻力，并且随着截面的复杂性，此现象愈发明显［3］。

表2 竖向极限荷载下复杂截面的端阻力和承台土阻力

图6 双室墙极限荷载下端阻力云图

图7 四室墙极限荷载下端阻力云图

图8 六室墙极限荷载下端阻力云图

3 内侧摩阻力

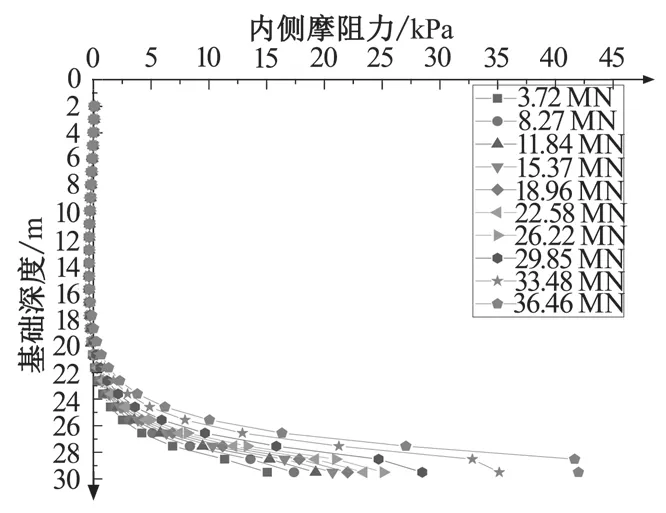
图9 双格室墙中点内侧摩阻力

图10 四格室墙中点内侧摩阻力

图11 六格室墙中点内侧摩阻力

图 9～图 11 为 10 个加载等级下的内侧摩阻力沿墙深的曲线图，曲线墙深 20 m 至基础顶墙体与内部土体没有相对位移，不存在摩擦力，到 20 m（约为 2/3 基础深度处）才开始出现，深度越大，内侧摩阻力亦越大。随墙芯数量的增加，墙芯给予基础下部的内侧摩阻力会变小，这是应力干扰效应，致使内侧摩阻力无法充分发挥。

4 承载力的计算

4.1 承载力的组成

根据上文的分析，对地连墙的承载力进行汇总计算，复杂截面的地连墙承载力Qw由以下分力组成，外侧土体对墙壁的外侧摩阻力Qfw、墙芯土体对内侧墙壁的内侧摩阻力Qfi以及墙端部土体提供的端阻力Qrb，见式（1）。

假设复杂截面的地连墙在达到极限承载状态时，基础内、外侧土体均已发生剪切破坏，外侧摩阻力Qfw通过土体的剪切强度最大值进行计算，见式（2）。

式中：Li地基第i层土深度；uw墙外侧矩形周长；qfw为地基第i层的极限侧摩阻力标准值，计算时可以参考相关地质勘察报告或者参照 JGJ 94-2008《建筑桩基技术规范》［4］表 3 相关规定进行取值。

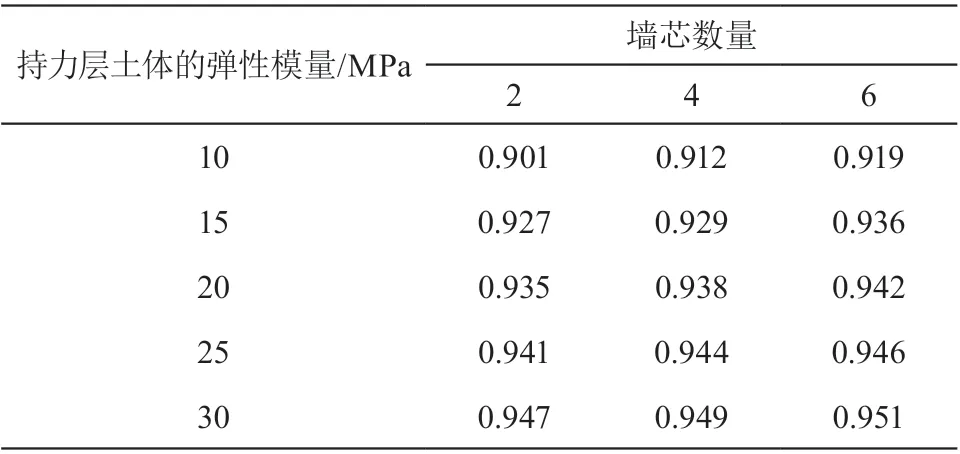
表3 隔墙效应系数 η

由上文可知，极限承载状态下，外墙的端阻力与内墙的端阻力的分布存在明显的差异，外墙大于内墙的阻力，并且随着截面的复杂性，此现象愈发明显。端阻力Qrb由外墙端阻力Qrbw和内墙端阻力Qrbi组成，见式（3）。

前文分析中三类复杂截面的地连墙基础的内侧摩阻力均从基础深度的2/3处开始出现，因此内侧摩阻力按照式（5）计算。

式中：Hi为深度 2/3 至端部各地基土的厚度；n为内部墙芯的数量；ui为墙芯周长；qfi取值同式（2）中外侧摩阻力qfw的取值进行取值。

分别将式（2）、式（4）和式（5）代入式（1）即可得复杂截面的竖向极限承载力见式（6）。

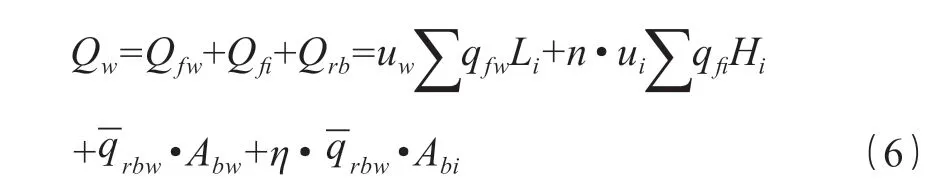
4.2 隔墙效应系数

在端部土体的材料参数中，土体的弹性模量对基础的承载影响最为显著，因此分别取不同模量的端部土体，研究效应系数与端部土体的弹性模量和墙芯数量的相关性。

表 3 反应了持力层土体的弹性模量与墙芯数量及效应系数的关系，可以看出：隔墙效应系数与墙芯数量呈微弱的正相关，但与土体的弹性模量呈强烈的正相关，在计算复杂截面地连墙的竖向极限承载力时可以根据表 3 的E值和n值估算η值。

5 地连墙承载力计算

5.1 工程概况

青森港湾大桥是一座全长 498 m 的三跨索面斜拉桥，该桥主跨 240 m，桥宽 25 m［5］。图 12 为青森港湾大桥的总体侧视图。青森港湾大桥其主塔 P9采用了六室型的地下连续墙基础，该基础是日本现有桥梁基础中截面尺寸最大且格室数目最多的复杂截面的地下连续墙基础，P9基础的详细几何构造如图 13、图 14 所示。

图12 青森港湾大桥总体侧面图（单位：cm）

图13 青森港湾大桥 P9 主塔基础（单位：mm）

东日本旅客铁道东北工事事务所的佐々木光春等人［6］报道了青森港湾大桥主塔 P9基础在实际施工荷载工况，根据沉降监测报告显示，P9基础最终沉降为 133.3 mm。

5.2 青森港湾大桥主塔基础工程的数值建模分析

对青森港湾大桥的 P9地连墙基础进行建模分析，根据当时地质勘查报告以及基础的截面尺寸建立有限元模型，建模中的参数如表 4 所示。

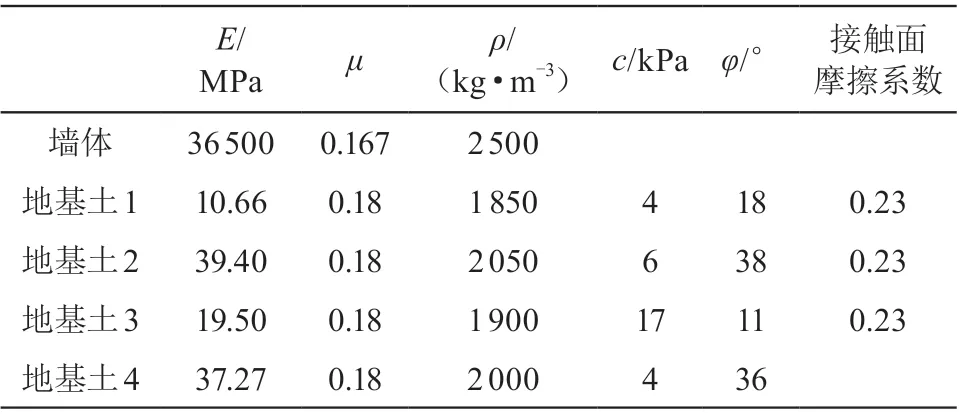
表4 建模参数

根据沉降监测报告简化当时的施工工况，根据现场工况拟确定基础的加载等级分为 7 级，如表 5 所示。

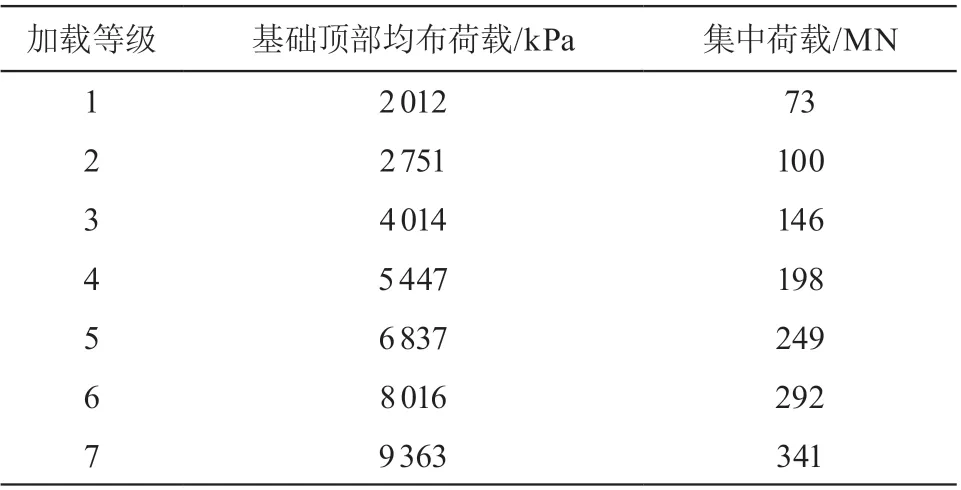
表5 加载等级

5.3 计算结果及分析

经分析，主室 P9基础由于自身整体性好、刚度大，呈现均匀沉降趋势。承台两端未发现沉降差，与现场实际情况符合。图 14 为数值计算得到的荷载Q-沉降s曲线与现场施工的沉降监测报告的荷载Q-沉降s曲线对比情况。2 条曲线大致可以分为 2 段。当加载量位于 0～250 MN 段时，2 条曲线大致为线性并呈现正相关，但是沉降监测报告中的沉降略大于有限元模拟的沉降。产生此原因是实际情况中沉积软土在弹性阶段受压时，其所受基础的压力与自身的压缩量并不是理想的线性的相关。当加载量位于 250～341 MN 段时，2 条曲线的斜率开始变大。沉降监测的沉降始终大于模拟值，在第 6 级荷载时 2 条曲线的沉降差最大，为 14.25 mm。产生此差异原因是现场施工工况较为复杂，沉积软土经过扰动后，应力场发生了变化，而数值模拟过程中，地基土体只存在竖向压应力，与实际现场存在些许差异。

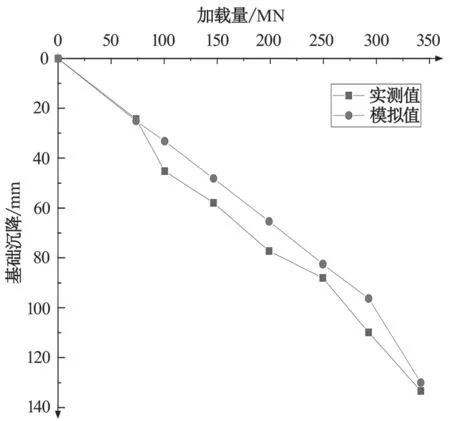
图14 基础的荷载 Q-沉降 s 曲线

由于曲线荷载沉降曲线较为平缓，没有陡降段，将Q-s曲线转化为 lgQ-s曲线，转化后的曲线如图 15 所示。可以看出，P9主室基础的竖向极限承载力为 341 MN，沉降监测报告中，P9主室基础最后一级荷载下的沉降量为 133 mm，与模拟的沉降值 128 mm 仅仅相差了 5 mm，说明本次数值模拟可以较好模拟 P9主室基础的承载过程。

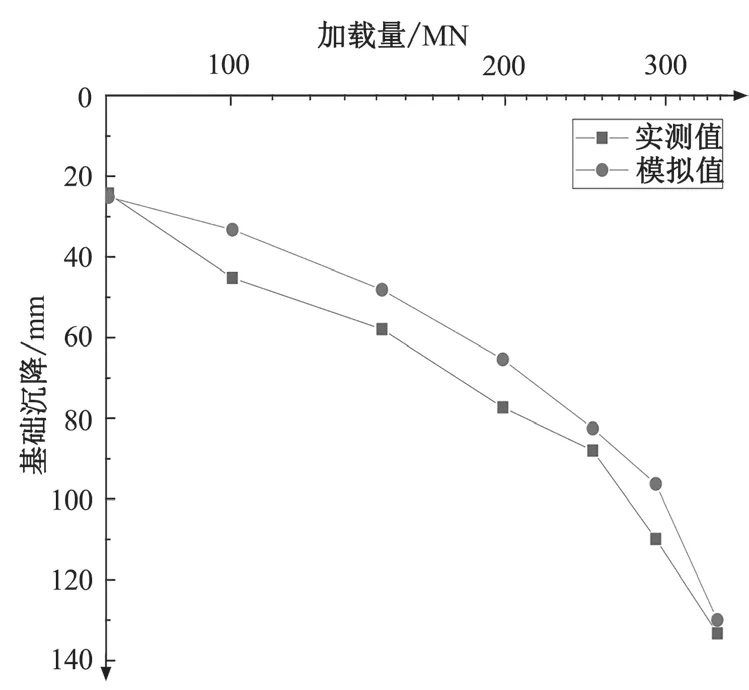
图15 基础的荷载 lgQ-沉降 s 曲线

根据式（6）复杂截面的地连墙的竖向极限承载力计算公式，参考 JGJ 94-2008《建筑桩基技术规范》中相关规定（见表 6、表 7），得出极限承载力为 384 MN，略大于实际的 341 MN。考虑到对土层进行了简化处理，故此式可以作为初步判断复杂截面的地连墙竖向承载力使用。

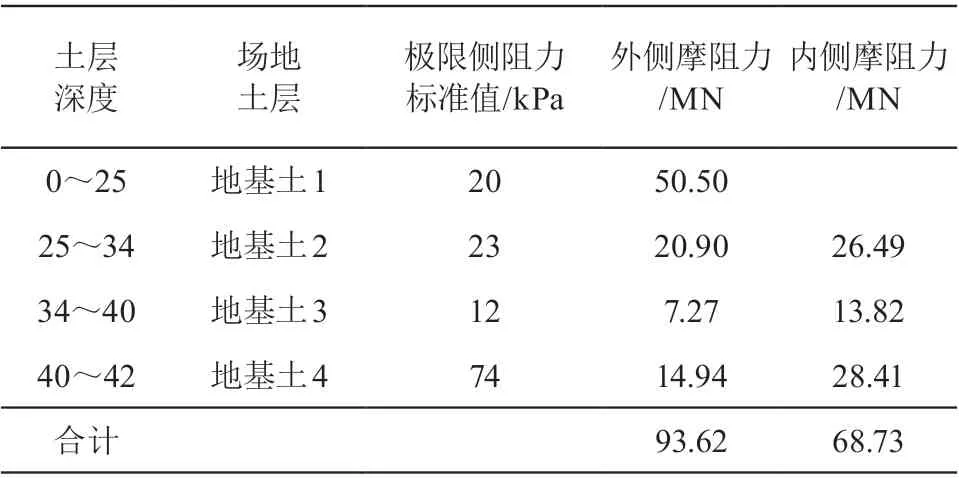
表6 侧摩阻力

表7 端阻力

6 结论

本文研究了复杂截面地连墙作为竖向承重基础时的竖向承载过程，分析了侧摩阻力以及端阻力随荷载的变化情况，并总结了复杂截面地连墙的竖向极限承载力公式，并得出以下结论。①当复杂截面的地连墙基础的内部墙芯的大小相同时，其竖向极限承载力并不会随墙芯数量的增加呈线性正相关，因为墙芯数量越多，内墙在端部会产生应力干扰效应，抑制复杂截面的地连墙的端阻力与内侧摩阻力的发挥。②在竖向极限荷载下，墙基础端部竖向应力差异较小，墙芯顶部的承台土阻力远远小于端阻力，对于竖向承载力发挥着较小的作用，可以略去。复杂截面的地连墙基础达到极限承载状态时，外墙的端阻力与内墙的端阻力的分布存在明显的差异，外墙大于内墙的阻力，并且随着截面的复杂性，此现象愈发明显。③复杂截面的地连墙基础的内侧摩阻力仅仅存在于端部附近区域，自 2/3 基础深度处至墙端部迅速增长，在端部达到最大值，墙芯端部土体较下部压缩量更大，深度越大，内侧摩阻力亦越大。随墙芯数量的增加，墙芯给予基础下部的内侧摩阻力会变小，这是应力干扰效应，致使内侧摩阻力无法充分发挥。④隔墙效应系数与墙芯数量呈微弱的正相关，但与土体的弹性压缩模量呈强烈的正相关，在计算复杂截面地连墙的竖向极限承载力时可以根据表 3 的弹性模量及墙芯数量估算η值。⑤六室墙基础拥有良好承载特性，适用于各种地质较差且对沉降要求较为苛刻的复杂环境中，该基础由于自身整体性好、刚度大呈现均匀沉降趋势，承台两端不会存在较大沉降差。⑥复杂截面的地连墙基础的承载力由外侧摩阻力、内侧摩阻力和端阻力组成，并且不同截面形状的地连墙由于内部墙芯的数量而存在较大差异，为了初步预估竖向极限承载力可以参考式（6）来进行初步判断。Q