逐阶自我训练 提升数学教师质疑水平

叶新和 (江苏省泰州医药高新区(高港区)教育局 225300)

陈 锋 (江苏省无锡市太湖格致中学 214125)

1 问题的提出

《义务教育数学课程标准(2011年版)》以及《普通高中数学课程标准(2017年版)》都在课程目标中提出：通过数学学习，学生能增强发现和提出问题的能力、分析和解决问题的能力．[1]8，[2]然而现实情况并不理想，人大复印资料《初中数学教与学》2020年第4期(专题：问题提出能力研究)的“编者按”指出：通过各类测评和调研发现，学生发现和提出问题的能力相对薄弱，而且很多教师对于引导学生从数学角度提出问题也缺乏有效的策略．[3]

笔者以为，之所以出现上述情况，主要原因在于教师自身质疑能力不够．要有效改变现状，首先要从提升教师自身质疑水平做起．

2022年2月19日，笔者登录“中国国家图书馆”读者门户云平台，在“期刊”栏选择“中国人民大学复印报刊资料”进行“高级搜索”：“数据库”选择“全文数据库”，“时间”选择“1995—2021”，“学科分类”选择“全选”，“关键词”为“质疑”并且“教师”，在“精确”与“模糊”中选择“模糊”，得到592条搜索结果，其中有4条与培养学生质疑能力有关，有1条部分内容对培养政治教师的质疑能力有所启迪，不过难以迁移．在中国知网选择“核心期刊”进行搜索，没有搜索到涉及教师自身质疑能力培养的文献．

看来对数学教师自身质疑能力的关注与培养目前可能是空白．通过一定训练不断提升数学教师自身的质疑水平虽然难度较大但既有价值也很必要．

2 进阶训练的探索

笔者试图从“内化”与“生长”两个角度来探索进阶训练的方法．“内化”指消化、吸收外界信息，结合到已有认知结构中．“生长”指观点、思路等由自身萌芽、发展而来．建构主义认为，学习过程是学生自己主动建构知识的过程．在新知识的学习中，学生往往基于以往经验去推出合乎逻辑的假设，新知识是以已有知识经验为生长点而“生长”起来的．[4]学习者在消化吸收或者在主动建构时可能遇到矛盾信息或者产生困难，此时如能进行审视与反思，产生的疑惑得以确认便会萌发“质疑”意识，在有意识训练中会不断发展“质疑”能力．

2.1 初级水平进阶训练

具备一定的质疑意识为初级水平，其表现为：对遇到的部分情境或者事情，会就其中的某个环节或者某个方面表示疑惑或者质疑，能够说出自己之所以有这样感觉的原因或者部分理由．可试从以下方面进行训练．

(1)阅读、学习商榷类文献

在中国知网“学术期刊”中“主题”选择“问题商榷”，“学科”选择“中等教育”进行搜索，可得到诸多文献，仔细阅读、感受进而形成质疑意识．

(2)对试题及其解答进行质疑

不妨从质疑中考试题、教材例习题开始．日常教研中发现很多一线教师认为中考试题不会有科学性问题，更是从未怀疑过教材中例习题会有问题，但实际上存在“千虑一失”的可能性．一旦教师发现有文献指出或者自行发现其中存在问题，那么其思想上受到的冲击会比较大，容易逐步树立质疑的意识．

对于具体试题而言，试题是否科学、答案是否正确、解法是否简洁客观性比较强，容易形成共识，可以从这些角度来进行质疑以提升数学教师自身质疑意识．

案例1以下内容选自某教材，试加以质疑．

1)例题：2007年10月24日，我国成功发射“嫦娥1号”探月卫星，经绕地调相轨道、地月转移轨道飞行后，“嫦娥1号”于11月7日顺利进入绕月工作轨道，共飞行326 h，行程约1 800 000 km，其中在地月转移轨道飞行了436 600 km．试用科学记数法表示这两个行程．解：1 800 000 km=1.8×106km， 436 600 km=4.366×105km．[5]53

2)练习：用科学记数法表示下数：地球的半径大约为6 400 km．习题：用科学记数法表示下数：同步卫星在赤道上空大约36 000 000 m．[5]53-54教师用书中相应答案分别为6.4×103km,3.6×107．[6]53-54

分析 根据教材定义“一个大于10的数可以写成a×10n的形式，其中1≤a<10，n是正整数，这种记数法称为科学记数法”[5]52可知科学记数法表示的是“数”．“行程”是“量”，不是“数”，“用科学记数法表示行程”说法欠妥，建议修改为“试用科学记数法表示1 800 000,436 600”，解答过程为： 1 800 000=1.8×106，436 600=4.366×105．练习答案应该将单位去掉，为6.4×103．习题答案正确．

2.2 中级水平进阶训练

具备一定的质疑能力视为中级水平，通常表现为：对遇到的部分情境或者事情，会对其中的某些环节或者某些方面表示质疑，能从逻辑角度利用推理(包括合情推理)的方式说出原因或者理由．可试从以下方面进行训练：

(1)学习逻辑方面的有关知识、方法

阅读入门类著作,如杨树森编著的《普通逻辑学》(第四版)，并努力应用于审视日常生活中的行为、观念等．

案例2以下内容选自某教育专著，试判断表述是否符合逻辑．

1)教师的工作不是传授知识，也不是促进学习，而是为学生营造有效的学习环境．有效学习环境的关键特征是，它们能让学生参与进来，让教师、学习者及其同伴确保学习朝着预期的方向进行．[7]69

2)本章提供了一些教师可用的向学生提供促进学习的反馈的实用技术．[7]152

分析 “不是促进学习，而是为学生营造有效的学习环境”，表述自相矛盾．作者认为“有效学习环境”能够“确保学习朝着预期的方向进行”，这表明“营造有效的学习环境”(手段)能够“促进学习”(目的)．

“教师给学生提供促进学习的反馈”，这与“教师的工作不是促进学习”相矛盾．

“教师的工作不是传授知识，也不是促进学习”与事实矛盾．实际上传授知识、促进学习都应该是教师的工作，只不过后者更加重要．

(2)评价权威试题的编拟

对权威试题的编拟进行评价，主观性比较强，要提出令人信服的不同看法甚至加以否定，难度往往会比较大，评价者的质疑水平通常要比较高．评价的角度可以有多个．如果是中考试题，那么可从试题的信度、效度、难度、导向作用等角度来进行评价．如用于教学，则要站在学生立场来评价，如例习题的编写安排是否符合学生的认知规律、解答所需要的数学“四基”是否超出学生的接受能力，等等．

案例3以下为某九年级教材中的例题及解答，试进行质疑．

例题：如图1，水平放置的圆柱形排水管道的截面半径是0.6 m，其中水面高0.3 m．求截面上有水部分的面积(结果保留小数点后两位)．

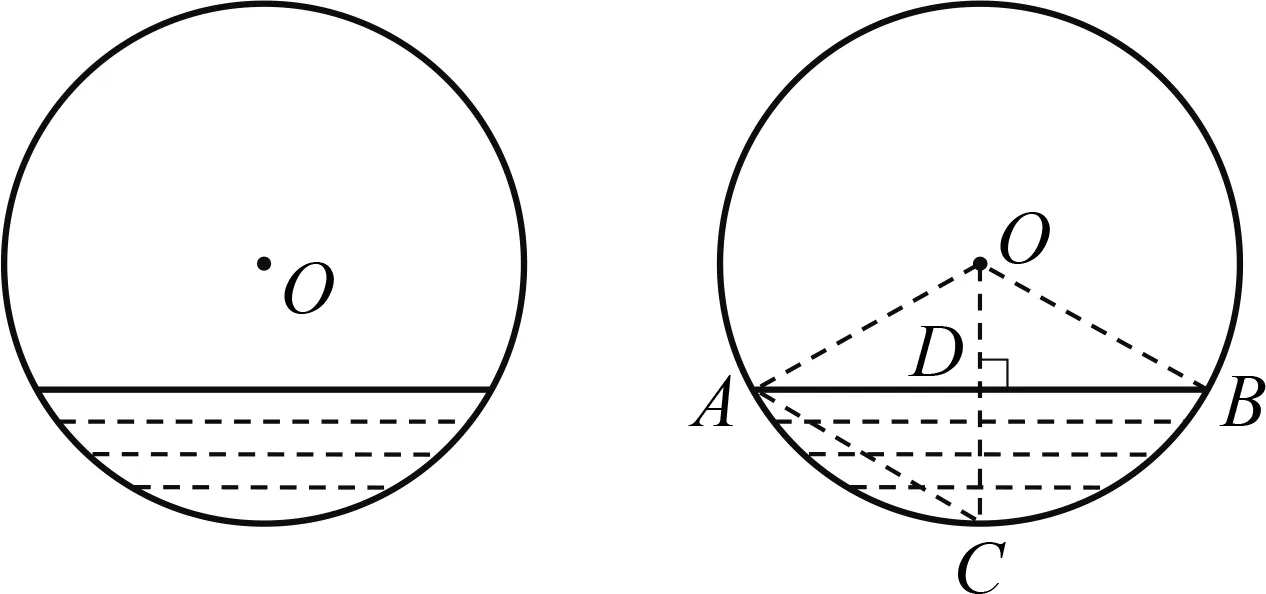
图1 图2

解：如图2，连结OA,OB，作弦AB的垂直平分线，垂足为D，交弧AB于点C，连结AC．

分析 水面是平面，“水面高”指水面和与之平行的参考平面间的距离，距离的确定要应用立体几何有关知识，这已超出九年级学生的接受能力．题目中仅告知“水平放置”，未指明参考平面，故线段CD长未必等于水面高，建议将“水面高”改为“水的最大深度”，解答时进行必要说明．

案例4以下内容选自某七年级教材与教师用书，试对试题及解答进行质疑．

试题：桌子上有3只杯口朝上的茶杯，每次翻转2只，能否经过若干次翻转使这3只杯子的杯口全部朝下？7只杯口朝上的茶杯，每次翻转3只，能否经过若干次翻转使这7只杯子的杯口全部朝下？如果用“+1”“-1”分别表示杯口“朝上”“朝下”，你能用有理数的运算说明理由吗？[5]63

答案：设杯口朝上记为“正”，3只杯口朝上的茶杯记为+1，+1，+1，这3个数的乘积为+1．每翻转2只杯子，即改变3个数中2个的符号，这3个数的乘积仍为+1.所以，3只杯口朝上的杯子，每次翻转2只，不能使杯口都朝下；7只杯口朝上的茶杯，每次翻转3只，可以经过若干次翻转使杯口全部朝下．[6]63

分析 “每翻转2只杯子，即改变3个数中2个的符号”，对此表述学生感到难以理解：“翻2只杯子”跟“改变2个数的符号”有什么关系？这需要分为两步来理解．

首先要理解茶杯翻转效果：翻转1次茶杯，相当于将表示杯口方向的数进行1次乘以-1的运算．或许可以这样来帮助学生理解：翻转1次茶杯，“杯口朝向”发生了改变，对应地，数a乘以-1得到其相反数-a．翻转奇数次，杯口朝向发生改变；翻转偶数次，杯口朝向不变．相对应地，(-1)2n+1结果为 -1，(-1)2n结果为+1．其次要理解乘法原理,原理内容可借助实例来理解．因为关注的是“所有杯口的朝向”，改变其中一只的朝向只是完成任务的一个步骤，要应用乘法原理来解决,这样，“1次翻转2只杯子”看成是其中的2个数同时乘以-1，或者说“改变其中2个的符号”．

基于上述分析，笔者以为试题的解答是超出七年级学生接受能力的．

用“+1”表示杯口“朝上”时“朝下”用“-1”表示，这是需要推理的，编者直接给出，其意图可能是为减少学生理解难度，不过因为没有揭示出翻转茶杯的效果，意图难以达成.也许可做如下修改：如果用“+1”表示杯口“朝上”，翻转一次茶杯相当于将表示杯口的数乘以-1，你能用有理数的乘法运算说明理由吗?

2.3 高级水平进阶训练

当质疑成为思维方式时，往往意味着质疑能力已达到高级水平，可从广度、深度层面进行描述：对所遇到的事情或者情境，习惯于找出行为背后隐含的假设或者观念，习惯于审视之后再接受或者反对，有足够证据来支撑自己观点．可试从以下方面进行训练：

(1)学习系统思维、辩证思维等有关论著，如《思维力：高效的系统思维》(王世民)、《哲学思维方式与领导工作方法》(韩庆祥等)，自觉用于审视日常教育教学、教科研中行为、观念以及背后隐藏的假设，等等．

(2)对教材内容的编写提出自己的不同看法，并努力提供比较充分的理由或者证据．对教材内容的编写进行质疑，主要从是否超出学生的接受能力、是否符合学生的认知规律、能否更好地突显学科育人价值、能否改进与优化等方面思考．

案例5以下为某版本教材中“平方根”主要内容[9]，试进行质疑与修改．

第1课时：

(1)情境：试计算小方格纸中线段AB,A′B′的长.提出问题：研究当x2=a时，x是什么数？(2)探索活动.(3)引入平方根定义与表示.(4)探索平方根的特征.(5)例题教学，例1：求一个正数的平方根．

第2课时：

(1)算术平方根定义.(2)例题教学，例2：求正数的算术平方根；例3：判断含根号的式子是否有意义；例4：解决简单的实际问题．

分析 此处内容的编排给人感觉在牵着学生鼻子走：在学生经验中线段长只能是正数，而正数的平方根有一正一负两个．利用线段长作为平方根情境，这与学生已有经验不一致，接受会有难度．当学生调节已有认知结构刚接受平方根知识时，接着学习算术平方根，回到结果是一个的情形，又要再次调整认知结构．此时再看情境，难免认为“平方根”定义与特征的学习是多此一举．

案例6试将案例4中“翻茶杯”问题修改为数学活动素材以体现学科育人价值．

分析 从“学科育人”角度看，学生不断在操作中试着用数学的眼光来观察、用数学的思维来思考、用数学的语言来表达，从而逐步发展学科关键能力、提升学科核心素养．试提供一种活动素材如下：

(1)7只杯口朝上的茶杯，每次翻转3只，能否经过若干次翻转使这7只杯子的杯口全部朝下?如能，提供一种翻转方法．

(2)桌子上有3只杯口朝上的茶杯，每次翻转2只，能否经过若干次翻转使这3只杯子的杯口全部朝下?如果不能，试说明理由．

(3)如果杯子为7只，每次翻转2只呢？

(4)如果杯子只数为奇数，每次翻转2只，你有何猜测？试说明你的猜测是正确的．

(5)如果杯子只数为7数，每次翻转4只，你有何猜测？试说明你的猜测是正确的．

(6)如果杯子只数为奇数m，每次翻转n只(其中m>n，n为偶数)，你有何猜测？你能够说明猜测是正确的吗?

(7)如果杯子只数为m，每次翻转n只(其中m,n为正整数，m>n)，你能够提出数学问题吗？

第(2)问可以通过试验得解：最初状态为“3上”，第1次翻转后为“2下、1上”，此时无论选择哪2只翻转，要么是回到“3上”状态，要么还是“2下、1上”状态，均为无效翻转，因此不可能变成“3下”情况．

第(3)问中杯子个数较多，再用试验的方法解答会比较繁琐.引导学生回顾、分析第(2)问中试验，发现不考虑茶杯位置影响时有两种无效翻转：一是将杯口分别朝上、朝下的茶杯各翻转1次；二是将杯口方向相同的茶杯翻转2次．利用该结论可以比较简便地解答第(3)问：翻转3次后为“6下、1上”，此时选择“1下、1上”或者“2下”进行翻转都是无效翻转，所以不可能全部朝下．该思路可用于解答 问题(4)．

当一次翻转4只茶杯时，进行第二次翻转便需要分类讨论，第(5)问用试验的方法会不胜其繁．仍然回顾、分析问题(2)中翻转，研究翻转次数可以发现：杯口要改变朝向，每只茶杯要翻转奇数次，3个奇数相加，和仍然为奇数．每次翻转2只，翻转正整数次，翻转总次数均为偶数．由于偶数不可能等于奇数，因此不可能杯口全部朝下．该思路考虑的是必要条件，必要条件满足不了，当然无法完成要求，由于没有考虑充分条件因此显得比较简洁．在不断翻转中继续引导学生观察、体会，发现翻转1次茶杯，其效果相当于将表示杯口方向的数乘以-1，在此基础上再让学生理解用有理数乘法运算解答的思路会容易些．这两种思路都容易迁移用于解决问题(6)．

3 说明与建议

(1)提升质疑水平，重要的是多学习、多运用．要尽可能多阅读经典著作或者权威文献，以尽快形成自身正确的认知结构和完善的思维方式．运用时可以选择熟悉的内容进行，还要重视对自身的质疑．要努力寻找出隐含在行为背后的假设再质疑．因为观念决定行为，不少时候审视行为背后隐藏的假设往往能够发现问题．

(2)形成质疑习惯，养成质疑的思维方式，意味着不被表象所迷惑或者误导，对于外界信息会进行符合逻辑的判断与推理，形成正确的、深刻的认识．既不要为质疑而质疑，也不要满足于质疑，对于发现的问题要努力提出建设性解决办法，以有效提升自身能力的同时具有较好的应用价值．

(3)提升教师自身质疑能力主要意图是培养学生发现问题能力．学生自己发现和提出问题是创新的基础[1]7，教学中要指向学生创新意识的培养，为国家培养具有创新精神的人才．

(4)笔者试图提供有效训练思路，对涉及的教材内容也尽可能给出改进建议．思路适用性如何，建议是否妥当，欢迎读者质疑．此外，是否有其他有效训练方法，感兴趣者可以继续研究．