基于增量动力法的电梯对重系统地震易损性分析
2022-11-16韩庆华张晓龙芦燕王力晨
韩庆华,张晓龙,芦燕,王力晨
(1.中国地震局地震工程综合模拟与城乡抗震韧性重点实验室(天津大学),天津 300350;2.滨海土木工程结构与安全教育部重点实验室(天津大学),天津 300350;3.天津大学建筑工程学院,天津 300350)
引言
非结构构件是指建筑中结构部分以外的所有构件,包括建筑非结构构件和附属机电设备[1]。典型的非结构构件包含吊顶系统、管道系统、幕墙和电梯等,其中电梯是连通建筑各楼层的固定式升降设备,根据升降原理不同分为液压式和曳引式两大类[2],曳引式电梯因其提升速度快、节能高效,在高层建筑中广泛应用。如图1所示,在曳引式电梯中,对重与轿厢通过曳引绳连接并通过导靴沿导轨做升降运动。对重装置由对重架、对重块、紧固件、延伸件和导靴等部分组成,具有平衡轿厢自重和一部分载荷重量的作用,可改善电梯曳引性能、减小曳引机功率。

图1 曳引电梯基本结构Fig.1 Basic structure of traction elevator
电梯的抗震性能直接关系到乘客人身安全、影响震后建筑内重要仪器设备撤离、抢险救灾以及对结构进行修复的速度,尤其对于医院、应急指挥中心及其它重点设防建筑,应保证电梯在地震后能够继续运行[3-4]。如表1所示,多次震害调查都显示电梯在地震中受损严重[5-7],这表明电梯的抗震性能薄弱,且在各种损害形式中对重系统受损所占比例最高,典型破坏类型如图2所示。同时,调查还发现有些建筑物未发生影响电梯正常运行的地震损坏,但其附属电梯却损坏严重[8],表明电梯与主体结构相比,在地震作用下更易发生损坏,存在主体结构与电梯抗震设防目标不匹配的现象。因此,深入开展电梯系统抗震性能研究,进行电梯震后功能状况评估和震害预测是一个亟需解决的问题。

图2 电梯对重系统地震损害[2]Fig.2 Earthquake damages of elevator counterweight system[2]
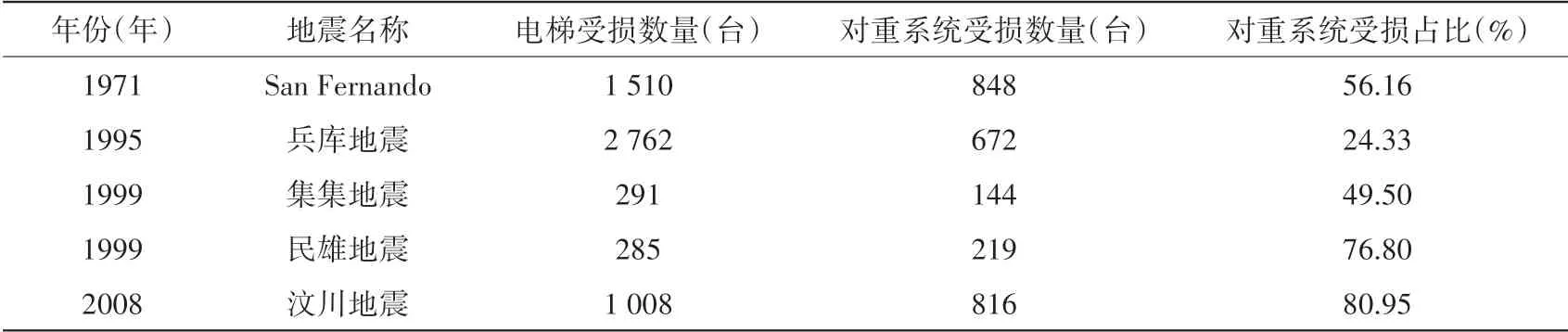
表1 震后电梯受损情况统计[7]Table 1 Statistics of elevator damages after earthquakes[7]
国内外学者在电梯抗震方面进行了持续的研究。Singh等[9-10]建立了对重-导轨-支架体系平面内及平面外动力响应的非线性分析模型,对重-导轨体系的地震响应特性进行了一系列研究。研究结果表明:对重-导轨系统平面内响应强于平面外,并且电梯系统的响应受到主体结构动力特性的影响。针对电梯对重系统抗震性能薄弱的问题,Singh等[11-13]将对重质量的一部分配置为质量阻尼器,提出了主动与半主动振动控制措施,以导轨/支架应力超过材料屈服强度为失效指标,开展了对重-导轨体系地震易损性研究,对比了不同减振措施的有效性。吕风英等[7,14]开展了电梯对重-导轨系统足尺模型振动台试验,采用ANSYS有限元软件建立有限元分析模型,对电梯对重系统在地震作用下的动力响应规律进行了研究。作为一幢5层建筑足尺模型振动台试验项目的一部分,Wang等[2]对该建筑物内曳引电梯在不同强度地震作用下的响应特征进行了观测,研究了主体结构与电梯以及电梯各部件之间的相互作用。
综上所述,目前对于电梯对重系统抗震性能的研究大多是基于一定的简化与假设,通过建立电梯对重系统数值模型,研究其在地震作用下的动力响应规律,提出减小振动响应的措施,但是对电梯对重系统震后功能状况进行评估和震害预测的研究较少。文中以某大型综合体建筑为工程背景,将基于性能的抗震设计方法引入到电梯系统抗震性能分析中,通过有限元软件建立多种典型对重位置的对重系统数值分析模型,考虑主体结构对对重系统动力响应的影响,开展对重系统地震易损性分析,为对重系统震后损伤评估和震害预测提供理论依据。
1 电梯对重系统数值模型
1.1 数值模型建立及验证
基于已有的电梯对重系统振动台试验[7,14],使用有限元软件ANSYS建立电梯对重系统数值模型。试验模型[7,14]示意图如图3所示,采用固定滑动导靴与TK5A型空心导轨,对重采用铅制对重块,除对重外的所有构件均采用Q235钢。试验中在对重右侧的导轨上布置加速度传感器,布置位置如图4所示。模型中各构件尺寸参数均参照试验中试件尺寸,如表2所示。

表2 构件尺寸参数[14]Table 2 Dimensional parameters of components[14]
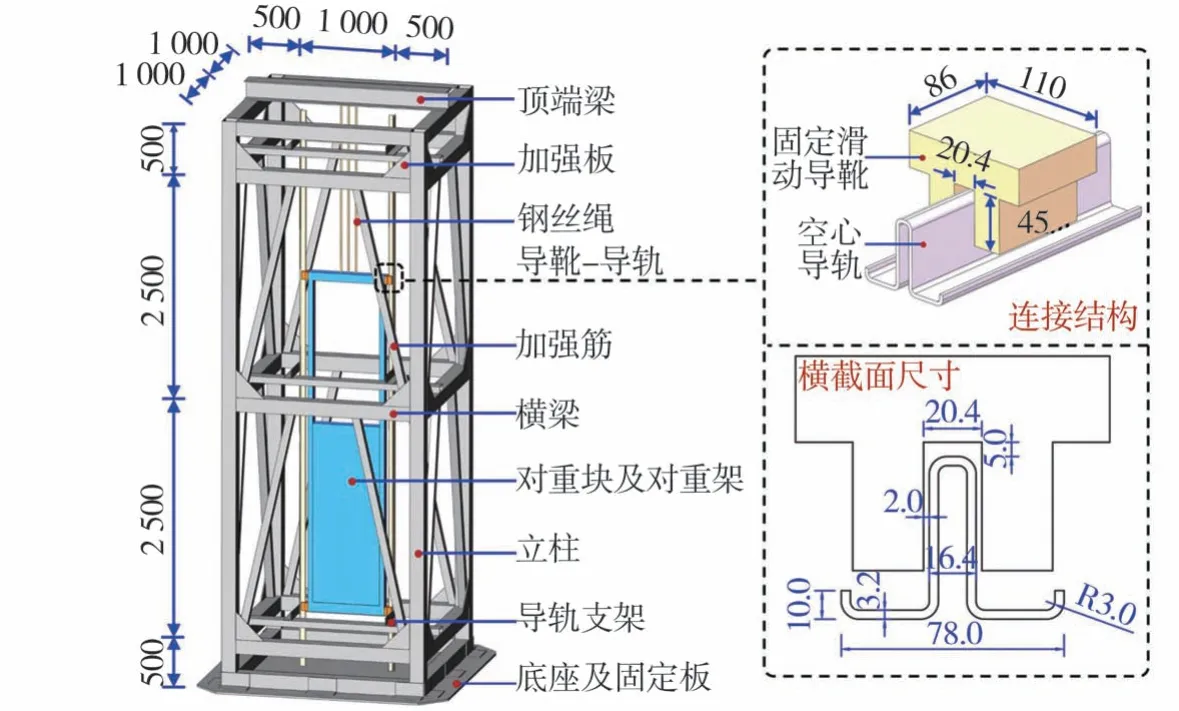
图3 电梯对重系统试验模型示意图(单位:mm)Fig.3 Schematic diagram of elevator counterweight system test model(Unit:mm)
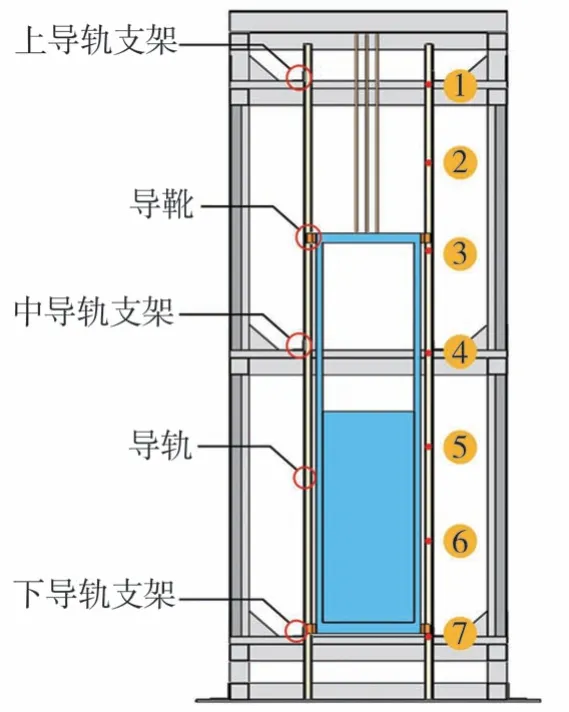
图4 加速度传感器布置图[14]Fig.4 Arrangement of acceleration sensor[14]
电梯对重系统数值模型如图5所示,钢材本构采用双线性随动强化模型(BKIN),考虑包辛格效应。电梯框架及导轨支架采用BEAM188单元,钢丝绳采用LINK180单元,将对重架与对重简化为均质连续体,对重与导靴采用SOLID45单元模拟。导轨采用梁单元和实体单元组合建模的方式,与导靴接触处的导轨采用实体单元,其余部分采用梁单元。导靴与导轨之间设置为面-面接触,采用CONTA173和TARGE170单元模拟。由于地震作用下导靴-导轨处于反复的分离-碰撞状态,忽略摩擦作用,设置法向触刚度系数FKN为0.001,设置关键项KEYOPT(10)=1更新接触刚度,以帮助模型收敛,减少迭代次数。约束模型底部3个方向的平动自由度和转动自由度。

图5 电梯对重系统数值模型Fig.5 Numerical model of elevator counterweight system
模态分析显示对重系统自振频率的数值模拟结果与试验结果误差较小,如表3所示。选取试验中[7,14]采用的汶川地震实测的茂县台地震动,将峰值加速度分别调幅为0.3、0.4、0.5g,沿模型X方向(对重平面内方向)对电梯对重系统进行瞬态动力分析。导轨峰值加速度的数值模拟结果和试验结果对比如图6所示,二者具有一致的变化趋势,地震动峰值加速度为0.3、0.4、0.5g时导轨最大峰值加速度的绝对误差分别为9.96%、14.56%和2.31%,其余测点多数模拟值与试验值的绝对误差在25%以内。通过对比可知,电梯对重系统的数值模拟结果与试验测试值具有较好的吻合度,所建立的数值模型及建模方法可以有效地反映出试验结果。

表3 电梯对重系统自振频率对比Table 3 Comparison of natural frequency of elevator counterweight system
1.2 电梯对重系统分析模型
本研究以某高层建筑为工程背景,主体结构盈建科(YJK)模型如图7所示,高度186.55 m,地上46层,地下3层,为钢筋混凝土框架-核心筒结构体系。结构抗震设防烈度为8度,设计基本地震加速度为0.2 g,地震设计分组为第2组,场地类别为Ⅲ类[1],结构阻尼比ξ取0.05。场地特征周期为0.63 s,结构第一阶阵型为X向平动,第一平动周期为4.02 s。

图7 结构分析模型Fig.7 Structural analysis model
基于1.1节中电梯对重系统数值模型,按照工程案例的实际尺寸建立分析模型,如图8所示,电梯井尺寸为2.8 m×2.6 m,采用T89/B型导轨。根据导靴与导轨支架的相对位置,选取3种典型的对重位置,分别以对重下部导靴位于下导轨支架、对重中部位于中导轨支架、对重上部导靴位于上导轨支架建立对重系统数值模型分析工况1、工况2及工况3,如图9所示。工况1、工况2、工况3中对重下导靴与下导轨支架的距离分别为0、600、1 200 mm。模型在接触设置、材料参数及边界条件等方面与1.1节数值模型保持一致。
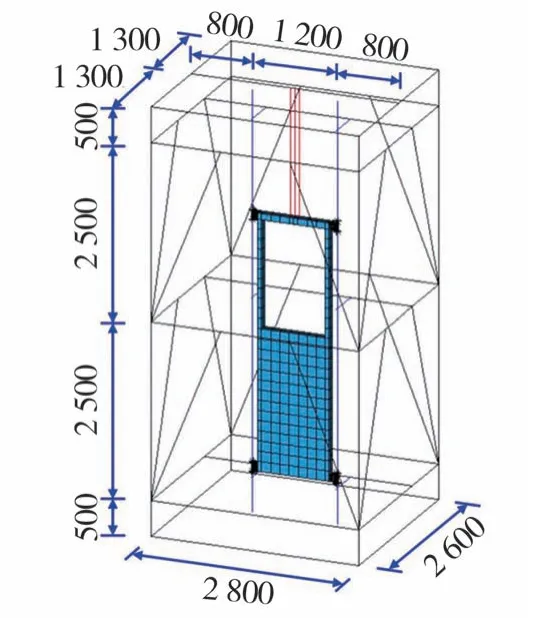
图8 模型尺寸参数(单位:mm)Fig.8 Dimensional parameters of counterweight system(Unit:mm)

图9 电梯对重系统分析模型(单位:mm)Fig.9 Analysis model of elevator counterweight system(Unit:mm)
2 电梯对重系统易损性分析方法
增量动力分析法(incremental dynamic analysis,IDA)是目前基于性能地震工程(performance-based earth‐quake engineering,PBEE)中主要用于确定结构在不同强度地震动作用下动力响应的一种方法[15]。本中研究将建筑结构基于性能的抗震设计方法引入到电梯对重系统抗震性能分析中,采用增量动力法开展了电梯对重系统地震易损性分析。
2.1 地震动选择
现有研究[15]表明,对中高层建筑结构抗震性能进行评估时,10~20条地震动记录能够产生足够的精度,作为中高层建筑内重要的附属设备,电梯系统抗震性能的评估可以此为参照。根据《建筑抗震设计规范》[1],按照场地类别及地震分组确定相应的设计反应谱,以结构基本周期点处对应的反应谱谱值相匹配为原则,通过目标反应谱在美国Pacific Earthquake Engineering Research Center(PEER)强震记录数据中筛选地震波。从平均意义上选入集集地震某台站记录的2个分量TCU115-E和TCU115-N,使地震波平均反应谱接近设计谱的要求[15]。综合考虑精度要求和计算成本,本研究选取15条地震动记录进行IDA分析,见表4所示。设计反应谱和所选择地震波的加速度反应谱如图10所示。
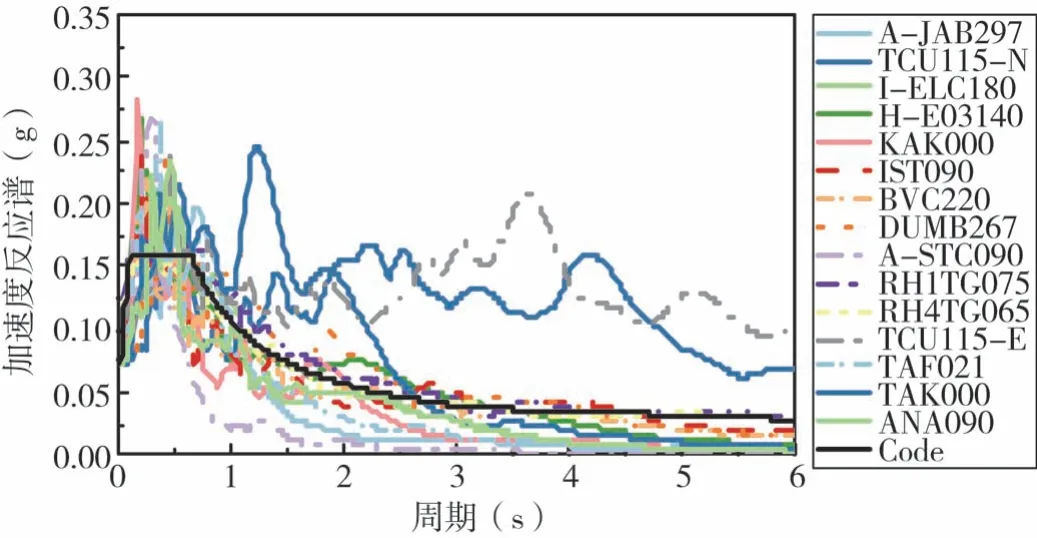
图10 地震动反应谱及设计反应谱(ξ=0.05)Fig.10 The response spectra of design and the selected earthquake records(ξ=0.05)

表4 用于增量动力分析的地震动信息Table 4 Ground motions information used for IDA
2.2 损伤状态及损伤指标的确定
地震作用下,对重对导轨的撞击力的大小与地震动的峰值加速度(PGA)有关,因此采用PGA作为地震动的强度指标。导靴与导轨在地震中处于反复的分离-碰撞状态,当导靴与导轨之间的脱开位移峰值大于两者的正常叠合长度时,就会发生导靴(对重)脱轨[14]。因此,选择导靴与导轨之间的脱开位移峰值与正常叠合长度之比R作为对重系统的损伤指标。参照文献[16]中建筑结构极限状态的划分方法,定义电梯对重系统的损伤状态,见表5所示。

表5 电梯对重系统损伤状态定义Table 5 Definition of damage state of elevator counterweight system
如图11所示,本研究分析模型中导靴与导轨顶面的间隙d=5 mm,导靴与导轨侧面的正常叠合长度L=40 mm,导轨导向面长度n=34 mm。当R≥1时,导靴与导轨之间的脱开位移峰值大于正常叠合长度,导靴脱离导轨,会导致电梯功能中断,脱轨后对重可能撞击其余电梯部件,产生二次灾害;根据《地震情况下的电梯要求》[17],定义导靴与导轨导向面的重叠长度小于5 mm,即0.875≤R<1时导靴发生严重振动,该规定与地震作用下导轨的许用挠度直接相关,发生严重振动时,导轨的变形超过许用挠度,直接影响电梯震后的正常使用,震后应更换撞击位置附近的导轨;以1/2导轨导向面长度作为分界值,定义导靴与导轨导向面重叠长度小于17 mm、大于5 mm,即0.575≤R<0.875时导靴发生中等振动,震后经专业人员排查检验后电梯即可继续运行;定义导靴与导轨导向面重叠长度大于17 mm,即R<0.575时导靴发生轻微振动,在安全位移范围内撞击导轨,基本不影响电梯的功能。
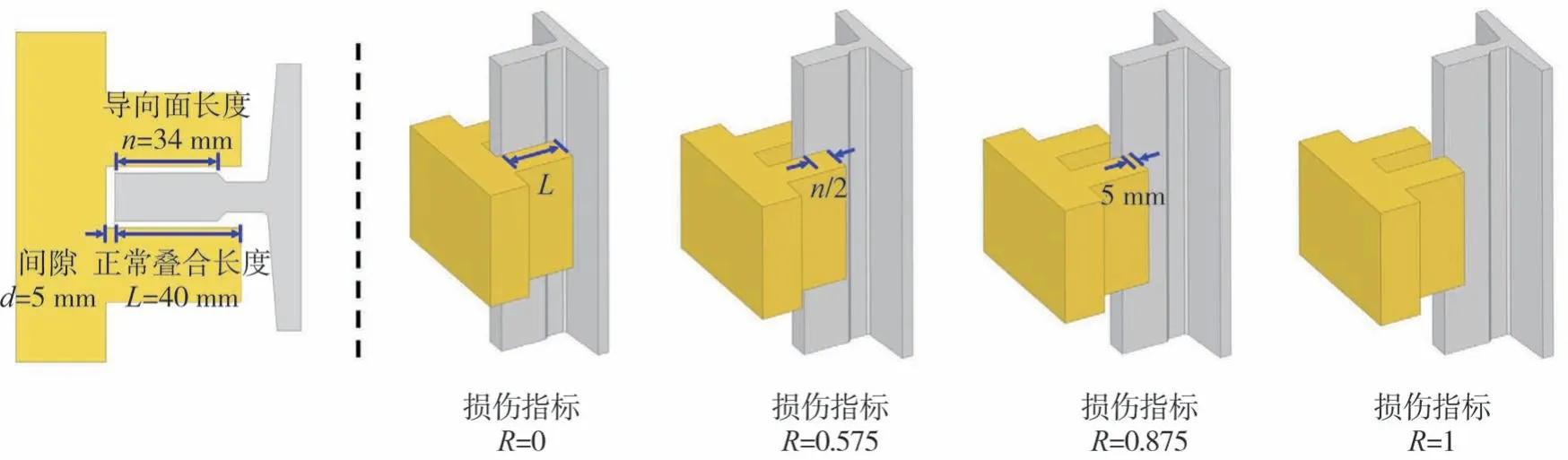
图11 导靴-导轨损伤状态示意Fig.11 Schematic diagram of guide shoe-guide rail damage state
3 电梯对重系统地震易损性分析
3.1 增量动力分析
电梯对重系统的动力响应受到主体结构振动特性的影响。在盈建科软件中对所选择的15条地震波进行调幅,对1.2节所述的主体结构开展动力弹塑性分析。由于地震动峰值加速度在0.4 g之后已属于非常罕遇的地震,发生概率较小;且考虑到结构塑性程度较高时,非线性分析会耗费大量时间[16],因此在0.4 g之后适当增大幅值,调幅后的PGA分别为0.1、0.2、0.3、0.4、0.6 g。不同地震动作用下,结构X方向(对重面内方向)最大楼面峰值加速度随PGA的变化如图12(a)所示。从图12(a)可以看出,结构楼层加速度响应与地震动输入相比,存在放大现象,且放大作用与地震波的频谱特性相关。以最大楼面峰值加速度与PGA的比值作为放大系数,定量描述主体结构对地震动的放大作用。由图12(b)可知,PGA为0.1、0.2、0.3、0.4、0.6 g时,加速度放大系数平均值分别为1.95、1.83、1.73、1.65、1.53,综合均值为1.73。由于主体结构对地震波的放大作用,对重系统受到的地震作用要强于主体结构,这也是多次地震中主体结构没有出现损伤,而电梯损坏的主要原因。

图12 最大楼面峰值加速度Fig.12 The maximum peak floor acceleration
将各地震动作用下最大楼面加速度响应时程曲线作为输入激励,对对重系统进行增量动力分析,并绘制各分析工况的IDA曲线,如图13所示。由图13可知,当PGA较小时,导靴对导轨的撞击力较小,导轨处于弹性变形阶段,IDA曲线基本呈线性变化;PGA大于0.1 g时,导轨开始产生弹塑性变形,刚度逐渐退化,IDA曲线斜率逐渐减小。不同地震动记录作用时,IDA曲线表现出一定的离散性。
3.2 易损性分析
基于IDA分析结果,计算对重系统振动响应超过某一损伤状态的概率。下面以中等振动的损伤状态为例说明具体计算过程。根据表5,电梯对重系统中等振动极限状态的损伤指标限值为0.575,根据IDA分析结果,计算脱开位移峰值与啮合长度之比的对数均值μlnR|PGA=x和对数标准差σlnR|PGA=x,按照式(1)计算不同PGA下脱开位移峰值与啮合长度之比超过0.575的概率,其中Φ(·)为标准正态累积分布函数。
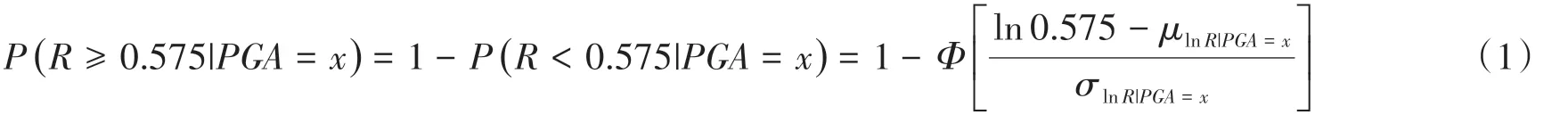
按照该方法计算进入每一个损伤状态的概率,以PGA为横轴、损伤状态的超越概率为纵轴绘制各工况电梯对重系统的地震易损性曲线,如图14所示。

图14 各工况对重系统易损性曲线Fig.14 Fragility curves of counterweight system under various working conditions
由图14可知,各工况对重系统易损性曲线的倾斜程度明显不同,表明对重系统的易损性与地震发生时对重所在的位置有关。以脱轨状态为例,在8度设防地震(0.2 g)作用下,工况1、工况2和工况3的超越概率分别为0%、2.63%、2.72%;在8度罕遇地震(0.4 g)作用下,工况1、工况2和工况3的超越概率分别为68.48%、82.52%、94.47%。与工况1、工况2相比,工况3更易发生脱轨破坏,这是由于对重块质心靠近下导靴,对重质量分布不均匀,下导靴对导轨的碰撞作用强于上导靴。工况1中对重下导靴位于导轨支架处,导轨支架在很大程度上减小了导轨的变形;工况3中对重下导靴远离导轨支架,导轨在下导靴的撞击作用下产生较大的变形,更易导致导靴脱轨;工况2中对重下导靴相比工况3更靠近导轨支架,导轨变形大小介于工况1和工况3之间。通过分析可知,当对重下导靴远离导轨支架时会使导轨产生较大的动力响应,减小导轨支架间距可使导靴尽可能的靠近导轨支架,是一种可以有效降低导轨动力响应的措施。易损性分析结果表明电梯对重系统的抗震性能较为薄弱,特别是在罕遇地震作用下发生对重脱轨现象的概率很大。
假定电梯正常运行时对重位于导轨不同位置的概率相等[13],综合考虑电梯对重系统的易损性。将对重每个位置的失效概率Pf-i与对重在该位置出现的概率进行相乘,由式(2)得到考虑对重位置的对重系统平均失效概率Pf。

式中:N为计算对重系统失效概率的对重位置工况数目。
对重系统整体易损性曲线和三水准地震易损性矩阵分别如图15和表6所示。

表6 对重系统的三水准地震易损性矩阵Table 6 Seismic fragility matrix for the given three ground motion levels of counterweight system

图15 对重系统整体易损性曲线Fig.15 Overall seismic fragility curve of counterweight system
由表6可知,当发生8度多遇地震时,电梯对重系统有2.40%的概率达到中等振动状态,达到严重振动与脱轨的概率基本为0;当发生8度设防地震时,对重系统达到中等振动的概率为44.84%,分别有4.35%、2.45%的概率达到严重振动和脱轨状态;当发生8度罕遇地震时,对重系统达到中等振动的概率接近100%,分别有89.58%和81.79%的概率达到严重振动和脱轨状态。通过以上分析可知,当主体结构满足抗震设计要求时,对重系统在各地震水准下可能发生不同程度的损伤,甚至是导靴脱轨现象。因而当前电梯的抗震设计与建筑结构“小震不坏,中震可修,大震不倒”的三水准抗震设防目标不相匹配,电梯对重系统的抗震性能有待提高。
4 结论
文中以某综合体建筑为算例,基于已有振动台试验建立了3种典型对重位置的对重系统数值分析模型。考虑主体结构振动特性对对重系统动力响应的影响,以导靴与导轨之间的脱开位移峰值与正常叠合长度之比作为对重系统的损伤指标,开展了对重系统地震易损性分析,主要结论如下:
(1)当主体结构受到水平地震作用时,由于结构固有振动特性的影响,楼层加速度响应与地震动输入相比,存在一定的放大现象,平均放大系数为1.73。因此,电梯对重系统所受到的地震作用要强于主体结构,在地震中更容易发生损伤。
(2)对重系统的易损性与地震发生时对重所在的位置有关。这是由于质量较大的对重块质心靠近下导靴,下导靴对导轨的碰撞作用强于上导靴,当对重下导靴远离导轨支架时,导轨在下导靴的撞击下产生较大的变形,更易发生对重脱轨现象。
(3)综合考虑3种典型对重位置的对重系统平均失效概率,得到8度设防地震作用下,对重系统分别有4.35%、2.45%的概率达到严重振动和脱轨状态;8度罕遇地震作用下,对重系统达到严重振动和脱轨状态的概率分别为89.58%和81.79%。因此,当主体结构满足抗震设防目标时,对重系统在各地震水准下可能发生不同程度的损伤,甚至是导靴脱轨这种严重破坏形式,表明对重系统的抗震性能有待提高。
(4)减小导轨支架间距可使导靴尽可能的靠近导轨支架,降低因导轨过大的动力响应导致对重发生脱轨的概率,是一种有效的电梯对重系统减振措施。
