R语言在概率统计课堂教学中的应用
——中心极限定理随机模拟
2022-11-16普映娟
吴 婷 普映娟
(保山学院 大数据学院,云南 保山 678000)
概率统计课本里的理论知识虽可以为学生提供理论基础,但却缺乏图形表达和模拟来增强理解与动手实践能力。在教学实践中,学生普遍认为中心极限理论晦涩难懂,教学效果不理想[1]。传统的黑板教学无法再满足学生课堂教学的需求[2]。因此,在概率论教学中,利用R语言的随机模拟和可视化将抽象概念转化为具体形象的图像,实验模拟的动态过程不仅可以加深学生对知识的理解,激发他们的想象力,从而促进反思,最终掌握知识,还可以提高课堂效率,使概率学习更具操作和动手空间,提高学生的实践能力。
1 中心极限定理
中心极限定理是相互独立的随机变量之和用正态分布近似的一类定理。直到20世纪30年代,中心极限定理的研究曾是概率论的中心内容。至今其仍是一个活跃的方向,推广的方向如独立不同分布乃至非独立的情形,由中心极限定理而引起的误差的估计,以及与之相关联的问题如大偏差问题之类[3]。最为著名的相互独立同分布情形下的中心极限定理,又称为列维-林德伯格中心极限定理。列维(1886-1971年)是法国数学家,对极限理论和随机过程理论做出杰出的贡献。林德伯格(1876-1932年)是芬兰数学家,因中心极限定理而闻名于世[4]。
定理1(列维-林德伯格中心极限定理)设随机变量序列X1,X2,…Xn中心相互独立同分布,若E(Xi)=μ,D(Xi)=σ2,且0<σ2< +∞,i=1,2,…,则对任意实数x,有

这个定理的直观意义是,当n足够大时,可以近似地认为。在实际问题中,若n较大,可以利用正态分布近似求得概率。
传统的教学就是列出不同条件下的中心极限定理,简单说明在样本量充分大时依分布收敛到正态分布。而证明过程在大多公共基础课的教材基本没有涉及到。即使教材给出了证明,作为公共基础课的学生也很少对其繁琐的推导过程感兴趣。故在讲授这项重要的知识点的时候,除理论说明和推导之外,还可以结合统计软件R进行教学,让学生切实体会到中心极限定理的魅力[4]。
本文将利用R软件生成n(n=1,2,3,4,30)个相互独立的均匀分布X~U(0,1)之和的模拟数据,绘制其直方图和密度函数图形。观察随着n的增大,n个相互独立的变量之和是否能用正态分布近似。本文将通过2种数据模拟的思路,来说明中心极限定理。一是进行随机采样,然后求和生成新的数据列,再查看和数据的分布情况;二是通过卷积推导出和变量的密度函数,然后分别绘制密度函数线,查看分布情况。设{}Xi为独立同分布的随机变量序列,其分布为区间(0,1)上的均匀分布,即Xi~U(0,1),i=1,2,…,30,且Xi之间相互独立。记,由中心极限定理可知,Yn~N(nμ,nσ2)。
2 R语言随机采样模拟
R语言是一款免费、开源的程序软件。它由新西兰奥克兰大学的Robert Gentleman和Ross Ihaka等人员共同开发,主要用于统计分析、数据挖掘以及数据可视化[2]。它不仅支持数据分析相关的多种算法,而且其语法也十分简明易懂,运行速度也可以接受,适合在教学和科研中使用。因此本文将利用R语言把概率论中的中心极限定理可视化,辅助教学。
随机采样模拟的思路:利用R语言中的随机数采样命令runif随机生成容量为10 000的30组数据,然后得到30组的模拟值,最后使用hist命令绘制每组数据的直方图,并增加其密度函数线。接下来运用R软件对其进行统计模拟并加以验证。
2.1 随机采样模拟的步骤
(1)随机生成容量为10 000的30组数据

(2)依次构造和变量Yn模拟数据

(3)绘制和变量Yn(n=1,2,3,30)的直方图和分布图

2.2 绘制直方图和分布图

图1 均匀分布随机采样生成 Yn(n=1,2,3,30)的直方图

图2 二项分布随机采样生成Yn(n=1,2,3,30)的直方图
3 R语言密度函数模拟
除可以通过采样的方式生成随机数,然后加和模拟,还可以通过卷积公式严格地推导出和变量的密度函数,用R软件直接绘制密度函数来观察分布情况。但随着变量的增多,计算会相当复杂,不易实现。
3.1 卷积公式
设(X,Y)是二维连续型随机变量,它们具有概率密度(fx,y),则Z=X+Y仍为连续型随机变量,其概率密度为。若X和Y相互独立,设(X,Y)关于X,Y的边缘概率密度分别为fX(x),fY(y),则上式化为

3.2 和变量的密度函数
设{Xi}为独立同分布的随机变量序列,其分布为区间(0,1)上的均匀分布,即Xi~U(0,1),i=1,2,3,4,且Xi之间相互独立。记,由中心极限定理可知,Yn~N(nμ,nσ2),令pn(y)为Yn的密度函数。根据卷积公式,可以依次求出Yn(n=1,2,3,4)的密度函数pn(y),n=1,2,3,4,如下公式(3.1)所示。

3.3 数据模拟的步骤和R代码
3.3.1 利用R语言依次构造Yn的密度函数pn

3.3.2 绘制Y1,Y2,Y3,Y4的密度图
根据构造Yn(n=1,2,3,4)的密度函数,利用R语言的curve函数绘制x∈[0,4]密度函数图。
3.4 模拟结果
根据上述步骤,将Yn(n=1,2,3,4)地密度函数p1(y),p2(y),p3(y),p4(y)表示在图3中。由图3可知:随着n的增加,pn(y)的图形愈来愈光滑,且越来越接近正态曲线,符合中心极限定理。

图3 Yn(n=1,2,3,4)的密度函数图
4 课堂教学案例(高尔顿钉板实验)
在《概率论与数理统计》学习中,在阐释完中心极限定理的基本定义后,增加中心极限定理的应用案例。高尔顿钉板实验常常作为应用实例,利用中心极限定理来进行解释。在课上展示环节,主要基于R软件,对高尔顿实验进行模拟,模拟多种情况,比如钉子层数的不同、实验小球的个数对于实验结果的影响等。
4.1 高尔顿钉板实验
有一个板上面有n排钉子,每排相邻的两个钉子之间的距离均相等。上一排钉子的水平位置恰巧位于下一排紧邻的两个钉子水平位置的正中间。从上端入口放入小球,在下落过程中小球碰到钉子后相等的可能性向左或向右偏离,碰到下一排相邻的两个钉子中的一个。如此继续下去,直到落入底部隔板中的一格,如图4所示。问当有大量的小球从上端依次放入,任其自由下落,小球最终在底板中堆积的形态。设钉子有16排,即n=16。
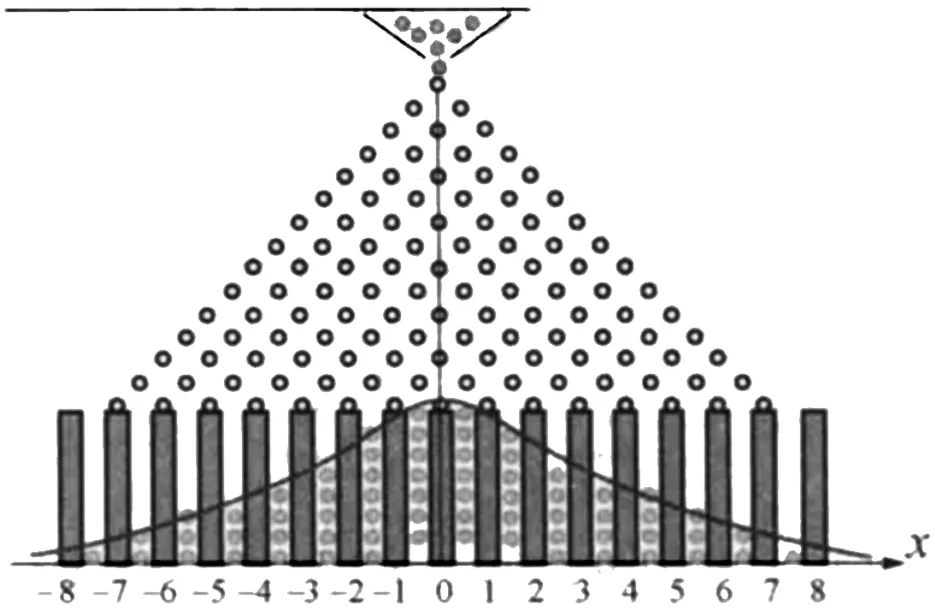
图4 高尔顿钉板
在街头赌博中,庄家会在高尔顿钢板的底板两端距离原点超出8格的位置放置了值钱的东西来吸引顾客,而在原点附近则放置相对便宜的东西或者不放置任何。一般在赌博游戏中,大多都是庄家赢,而这个游戏也不例外。我们可以用中心极限定理来揭穿这个街头赌博中的骗术。
若要考察小球堆积的形态,就需要考察小球最终下落在底部隔板的位置的分布。则设随机变量X为“小球最终下落在底部隔板中的位置”,同时引入随机变量Xi服从伯努利分布,分布律如表1所示。则μ=E(Xi)=0,σ2=D(Xi)=1。

表1 随机变量Xi的分布律

为揭穿这个街头赌博中的骗术,需要计算中大奖概率,即下落小球超出8格的位置的概率。设钉子有16排,即n=16。由于,此时X~N( )0,16,有

此时计算中大奖的概率不到5%,这说明顾客中大奖的可能性微乎其微。
4.2 R语言模拟实验
接下来通过软件模拟的方式,来模拟高尔顿钉板实验。
4.2.1 模拟生成落点数据
设定生成落点数据函数的输入、输出参数,如表2和表3所示。

表2 输入参数

表3 输出参数
下面是模拟生成落点数据的R函数实现。


4.2.2 绘制落点数据的直方图
由上述构造的R函数可以得到每个点的下落位置y,对下落位置绘制其直方图hist,同时增加临界位置8和-8,标识出中大奖的概率P(|X|>8)。

4.3 实验结果
根据上述步骤进行实验,得到在n=16排钉子下投掷分别M=10,100,1 000,10 000次落点的位置数据,可以得到结果如图5所示。在本次模拟下,仅投掷10次,此时获取大奖(P(|X|>8))的概率为0。当投掷次数达到100及以上,获取大奖的概率稳定在2%附近。同时,随着次数的增加,落点位置的分布更接近于正态分布。

图5 在16排钉子下投掷分别10,100,1 000,10 000次落点分布
但同时也注意到随着投掷次数的增加,获取大奖的概率稳定在2%附近,与上节正态分布计算出的概率4.56%存在差异。原因是层数n仅为16不足够大,正态近似程度不高。虽然能在一定程度上说明赌博问题,得到近似概率,但精确概率仍然需要通过卷积公式来求n重二项分布的和分布函数。
由此可以得到如下结论:
(1)试验测试较少时,一次性命中大奖几乎不可能。
(2)随着次数的增加,落点位置的分布接近于正态分布,符合中心极限定理。
(3)通过数据模拟得到的概率值与中心极限定理利用正态近似得到的概率相比,仍有差异。原因是层数n不足够大。但作为近似的判断也足够了,不影响对此赌博问题得到近似概率,精确概率仍然需要通过卷积公式来求n重二项分布的和分布函数。
5 结语
中心极限定理作为概率论与数理统计课程教学中的重点和难点之一,在教学过程中选择使用R语言随机模拟抽样和概率分布情况,不仅可以使学生能够较好地理解和掌握中心极限定理的本质,也能够训练学生的编程能力,增强其动手能力[6]。
在计算技术快速发展的今天,编程和数据模拟也是一项必备技能。大学课堂教学也应该与时俱进,充分利用现代化的教学工具和手段,让学生在学习传统知识的同时,领略现代科技的发展对一些学科的促进作用,从而激发学生的学习兴趣,培养学生利用现代技术手段解决问题的能力[5]。
