“老鼠出洞”问题的另两种奇思妙解
2022-11-16郭蓉
郭 蓉
甘肃省武威第一中学,甘肃 武威 733000
“老鼠出洞”问题,是一个经典而有趣的物理竞赛问题。经查阅大量对该问题研究的文献资料,发现文献[1-3]中只给出了积分法(或者微元法)和图像法两种求解的方法。因此,文献[1]认为因高中数学知识不足,直接应用积分法(或微元法)求解难度大,图像法是唯一的方法。文献[2]也用图像法做了分析。本文介绍竞赛训练时学生想到的另两种奇思妙解,以飨读者。
1 常见分析方法
问题一只老鼠出洞后沿直线奔跑,其速率与离开洞口的距离成反比。已知老鼠在距洞口距离为a的甲处时,其速率为v0。那么,当老鼠从甲处跑到距洞口距离为b(b>a)的乙处,所需时间是多少?
1.1 积分法
以洞口为坐标原点,以老鼠奔跑的直线建立直线坐标系。设老鼠在任意位置x处时的速率为v,则,k 为常数。由题意,x=a时,v=v0,则 k=av0。
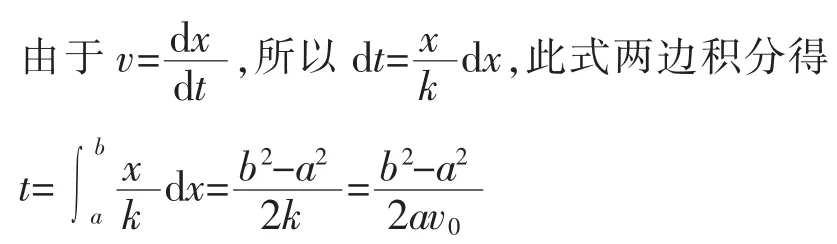
点评积分法的实质是微元求和取极限,即积分法和微元法的本质相同。由于大部分高中生没有熟练掌握数学积分知识,因此竞赛辅导中常用微元法分析。
1.2 图像法
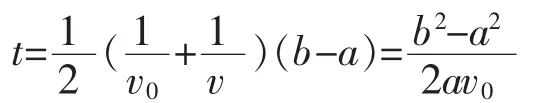
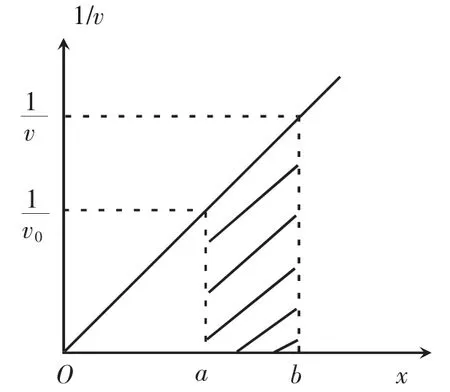
图1 图像
点评图像法是物理解题中常用的方法,在某些问题的求解中,物理图像可起到意想不到的效果。
2 另两种奇思妙解
2.1 等效转化法
等效转化法是常用的物理方法,也是高中生必备的物理学科核心素养。等效转化法的原则是效果要相同。实际应用时,一定要在保证效果相同的前提下,将陌生的、复杂的、不熟悉的、难处理的实际问题的分析,转化为与其等效的简单的、熟悉的问题的分析,以便抓住问题的本质,从而找到复杂问题的规律。
独特的设想若能找到一个简单而又熟悉的运动与老鼠的运动等效,则通过求解这个熟悉的运动所需的时间,可知道老鼠运动所需的时间。
精巧的构思由于老鼠运动速率v与位置坐标x成反比,即。设想一根弹簧一端固定在图2中坐标原点的左侧,另一端固定在一小滑块上,弹簧自由伸长时,滑块在洞口位置(坐标原点)。滑块离开洞口后向右运动,在光滑水平面上受向左的弹簧弹力,并设弹簧弹力F=k0x(k0为弹簧劲度系数)对滑块做功的功率P恒定不变,由力做功的功率公式P=Fv得滑块运动的速度

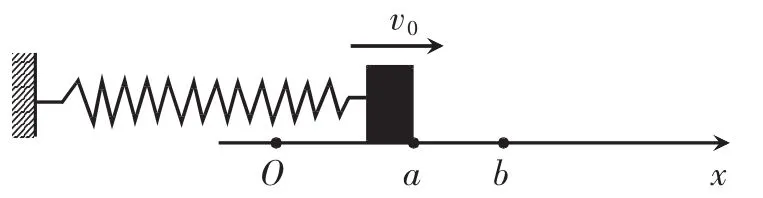
图2 等效转化的运动模型图
巧妙的计算由题意,当x=a时,v=v0,将其代入(1)式得

滑块从甲处到乙处的运动过程中,弹簧弹力对滑块做的功为
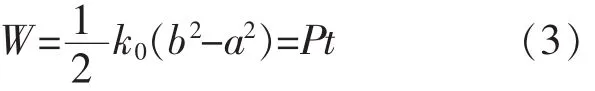
由(2)(3)式易得滑块从甲处运动到乙处的时间为

点评从独特的设想,到精巧的构思,再到巧妙的计算,体现了学生思维的独特性和创造性,也体现了学生解决问题中构建物理模型的能力。
2.2 类比猜想法
类比猜想法,是根据两个事物在某些属性上的相似性,类比猜想出其他属性也有可能具有相似性的认知思维方法。类比的基础,是要发现两个不同事物之间有某些相似性,从而利用已知事物的规律去类比探寻(猜想)未知事物的规律。类比猜想法具有一定的认知价值,是科学探究中常用的方法。
但是,类比猜想法是由个别到个别的非逻辑推理。因此,其结论的正确性需要用实验(或者其他方法)来进一步检验。如果类比的两个对象之间共有的属性越多,则类比出的结论的可靠性越大。
在“老鼠出洞”问题中,老鼠的运动虽然不能直接用已学过的运动学公式求解,但只要能找到描述老鼠运动的公式和学过的物理公式的数学形式相似,便可类比学过的公式形式推测出解决“老鼠出洞”问题的公式形式。但这样类比出的结果不一定正确,其结果还有待于用其他办法(或者实验)进一步验证。

类比对象初速度v0=0的匀加速直线运动的两个公式Δs=vΔt和v=at(式中Δs是极短时间Δt内的位移),所以在t时刻到t+Δt时刻所发生的位移为

显然,(5)(6)式的数学形式极为相似。
因此,由(5)(6)式找到物理量之间的对应关系:“老鼠出洞”问题中的时间t、位置坐标x、分别对应初速度为零的匀加速直线运动中的位移 s、时间 t、加速度 a 。
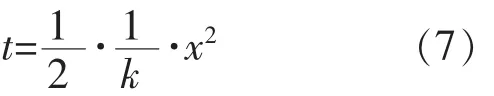
由于从洞口到甲处的时间为t1时,x1=a;从洞口到乙处的时间为 t2时,x2=b,则由(7)式得
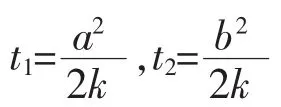
所以,老鼠从甲处到乙处所需时间为
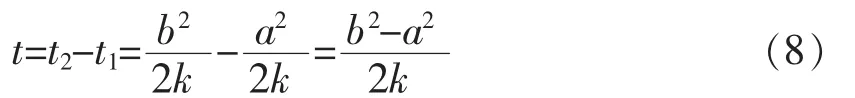
点评类比猜想法,是科学研究中的一种很重要的科学方法,也是一种创造性思维方法。上述求解方法也是一种奇思妙解,但考试中学生若采用这种方法,即使得出正确的结果,评卷判分时其思考的过程也可能并不能得分,这或许也是我们教学中值得深思的问题。
