高中物理研究极值问题的几种方法
2022-11-16吴晓明
吴晓明
合肥市第一中学,合肥 230601
在高中物理学习中,我们不仅借助于数学学习中严密的逻辑思维能力,还需要运用各类数学方法进行分析、讨论、推理、演算,从而最终得出结果。如果在物理学习中,依据物理原理建立起若干方程,却不会运用数学方法进行求解,依然功败垂成。因此,在高考考场上,凡是中学阶段学到的数学,如代数、三角、几何、解析几何等,都可以成为求解高考物理试题的数学工具。物理极值问题是物理与数学融合的典范,它既要求学生能正确分析物理情境、建立合理的物理模型,又要求学生具有较高的数学解题技巧[1]。通过大量的教学实践总结,高中物理中研究极值问题一般有以下几种方法。
1 运用一元二次方程的判别式求解极值问题
如果方程ax2+bx+c=0有实根,那么它的判别式一定满足条件Δ=b2-4ac≥0,利用这一性质,我们可以将待求物理量与自变量之间建立起一元二次函数关系,通过解不等式Δ=b2-4ac≥0,找出函数的极值。
例1如图1所示,用细线竖直悬挂一个质量为M的圆环,在环上套有两个相同的、质量均为m的光滑小球,现设法使两球从圆环最高点沿两侧由静止滑下,若下滑至某处悬绳的拉力恰好等于零,则m至少多大?
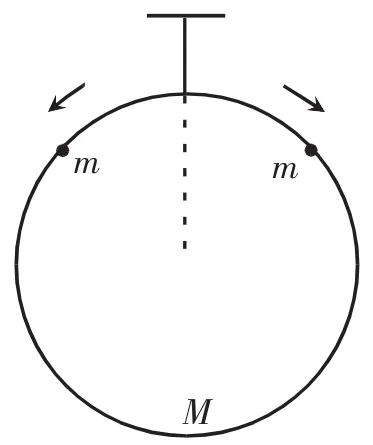
图1 例1图示
解析设圆环半径为R,取其中一个小球为研究对象,如图2所示,某时刻小球下滑到A点,此时小球与圆环圆心连线和竖直方向成θ角。

图2 例1解析图示
根据牛顿第二定律可知

整个下滑过程中,由机械能守恒可知
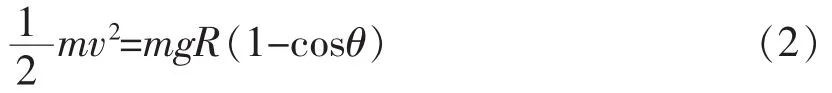
联立(1)(2)两式得

以圆环为研究对象,由平衡条件可知

将(3)式代入(4)式,得

2 运用三角函数求解极值问题
根据高中数学知识可知,函数y=acosθ+bsinθ,我们可以变化为:

例2如图3所示,质量为m的滑块以初速度v0从斜面底端沿斜面向上运动,滑块和斜面之间的动摩擦因数,重力加速度为g。若斜面倾斜角度可以调节,求:当斜面倾角为多大时,滑块滑行的最大距离最小?最小值是多少?

图3 例2图示
解:当θ变化时,设沿斜面向上为正方向,滑块的加速度为a,则:

滑块的滑行距离x满足:
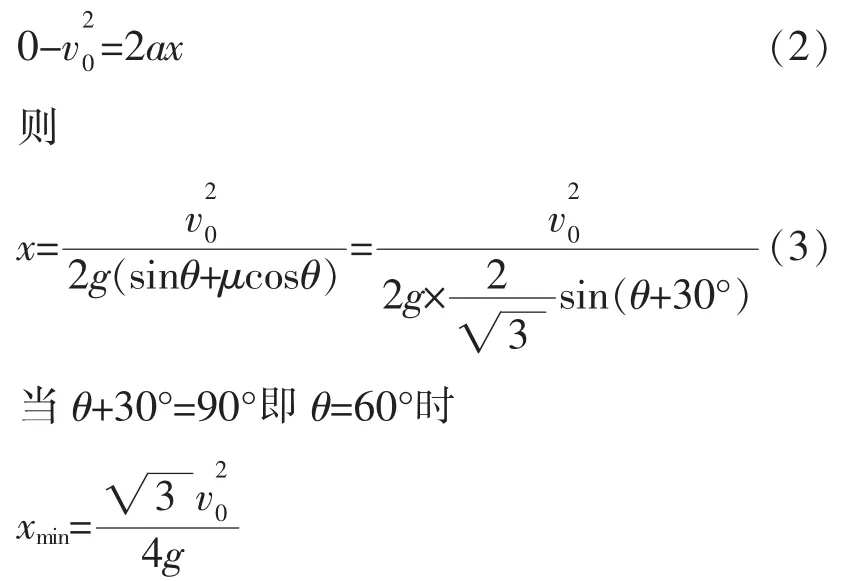
3 运用物理图像求解极值问题
中学数学学习中,我们常常借助图像来研究函数性质,如何将函数图像的几何特征与代数特征进行紧密结合,往往也是求解问题的关键所在。在高中物理定量分析问题中,除了通过物理规律建立起各种物理量的函数关系、进行代数联立求解以外,图像这种语言在传递信息的同时,也可以在特定情境下帮助我们简化代数运算、寻找出问题的答案。
例3如图4所示,在光滑的水平面上静置一质量为M、长度为L的木块,现有一质量为m的子弹以水平速度v0射向木块,若v0大小可随意调整,请问v0满足什么条件时,在整个子弹打击木块的过程中,木块获得的动能最大?不考虑子弹竖直方向的下落运动,假设子弹打入木块时二者之间相互作用力f大小保持不变,重力加速度为g。

图4 例3图示
解析如果子弹初速度太小,打击过程中,木块获得的动能肯定较少;子弹初速度不断增大时,木块动能是否持续增加呢?这显然需要定量的分析,如果以子弹初速度v0为自变量,木块动能为因变量,建立起函数关系寻找极值,代数运算会比较繁琐,我们不妨用v-t图像来展现这个过程,寻找答案。
如图5所示,v-t图像中阴影部分面积为子弹击穿木块的过程中二者的相对位移,即等于木块长度L。对比图6可知减小子弹初速度v0,由于子弹击穿木块的过程二者的相对位移保持不变,故而木块在此过程中获得的速度更大。由此分析可知,当满足子弹刚好击穿木块二者共速时,木块获得的动能最大。
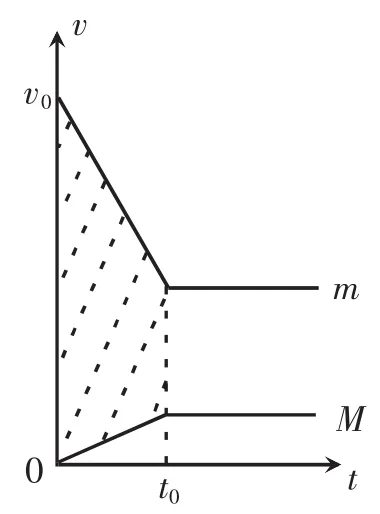
图 5 v-t图

图 6 v-t图
根据系统动量守恒定律可知

由能量守恒可知
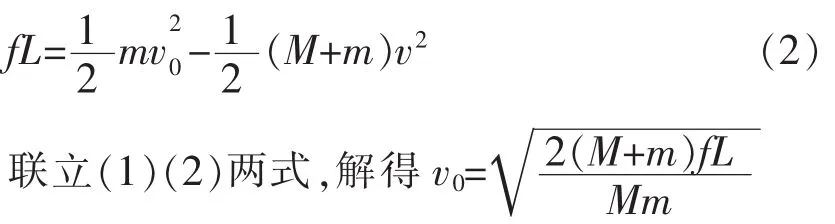
4 运用矢量三角形求解极值问题
由几何知识可知,从一点到某一直线垂线段最短。这一几何特征运用于高中物理求解问题时,往往被构建在矢量三角形中,利用矢量三角形分析求解动态平衡问题就是最好的例子(受篇幅限制,本文不再探讨该问题)。但是受这个知识点影响,在思维方式中,学生常常固化地认为矢量三角形只能求解动态平衡问题,其实矢量三角形也可以在分析其他矢量运算时助力极值问题求解。
例4某同学在距离地面高度h处以一定大小的速度v0斜抛一小球,当其速度与水平方向夹角不同时,落地点与抛出点的水平距离即射程大小也不同,不计空气阻力,则最大射程是多少?
解析设小球初速度方向与水平面夹角为α,空中运动时间为t,落地速度大小为v,与水平方向夹角为β,由机械能守恒可知:

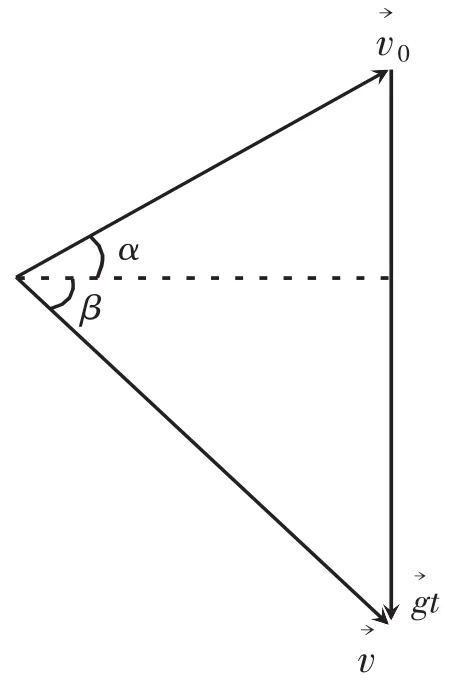
图7 例4解析图示
该三角形面积为

故当 α+β=90°时,S面积取极大值。
代入(1)(4)(5)式解得
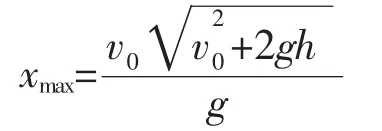
5 运用费马原理求解运动中的极值问题
1662年法国科学家皮埃尔·德·费马提出:过空间中两定点的光,实际路径总是光程(或者时间)最短。这是几何光学中一个最普通的基本原理,称为费马原理。用微分或变分法可以从费马原理导出以下三条几何光学定律:光在均匀介质(或者真空)中沿直线传播、光的反射定律、光的折射定律。折射定律涉及的介质折射率定义为,其中v是光在介质中的传播速度,c是光在真空中的传播速度,而光在两种不同介质面上折射时,有[2]。这一规律可以被用于运动学中当物体在两个不同的速度区域运动时与时间相关的问题,即类折射问题。
例5如图8所示,MN为沿着湖岸的一条笔直马路,路人甲行走到A点位置时,忽然听见湖中C点传来路人乙落水的求救声,落水点到马路的垂线段长,路人甲急忙奔跑至C点救人。已知xAB=30 m,路人甲在马路上奔跑速度v1=7 m/s,在水中游泳速度v2=1 m/s,请问路人甲奔跑至哪个位置入水游泳到C点位置所需时间最短?最短时间是多少?[3]

图8 例5图示
解析把路人甲视为光子,马路相当于“光疏介质”,湖水相当于“光密介质”。
如图9所示,路人甲沿着马路运动至D点跳入湖中,沿DC方向游向C点,类比折射定律可知
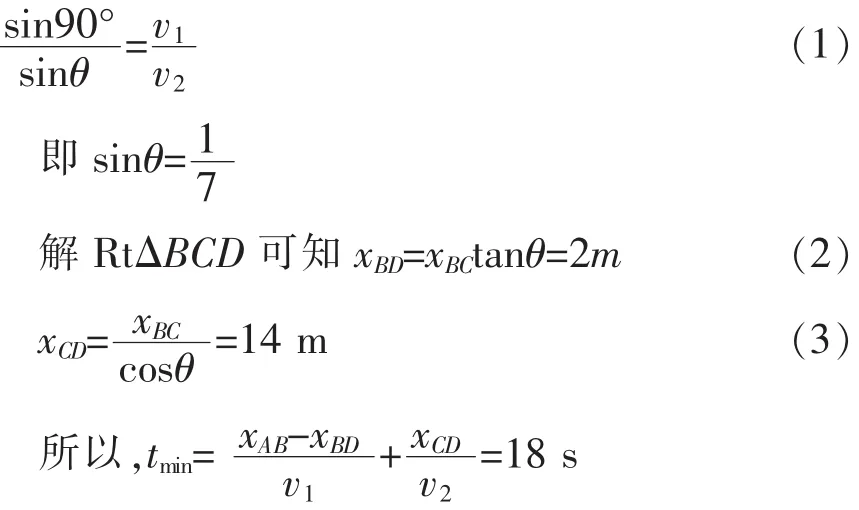
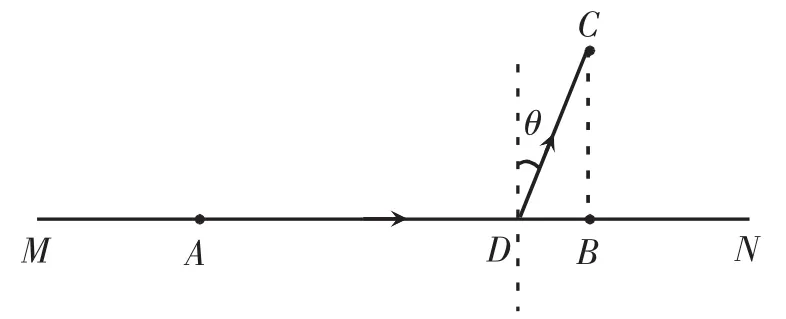
图9 例5解析图示
6 运用不等式求解极值问题
当我们根据物理条件列出不等式求解问题时,对计算式中“≤”“≥”符号的解读非常重要,其等号一般包含了极值条件。高中物理学习阶段,应用到的主要不等式为均值等式,即:

当且仅当a1=a2=a3=…=an时等号成立。
例6如图10所示,一根长为L的轻绳一端悬于O点,另一端连接一质量为m的小球(小球可视为质点),现将轻绳拉直至水平方向,此时小球处于与O点同一水平高度的M点,由静止释放,在小球下摆至最低点N的过程中,请问小球所受重力的最大瞬时功率是多少?
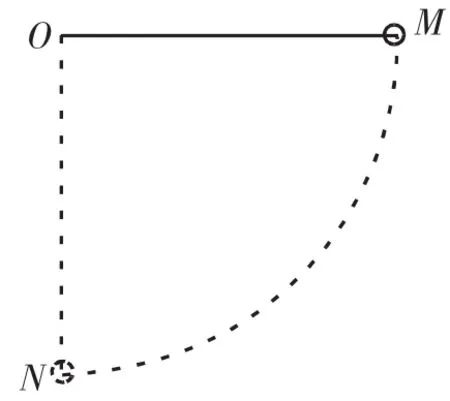
图10 例6图示
解析1如图11所示,设某时刻小球摆到A点,轻绳与水平方向的夹角为θ,小球速度为v。
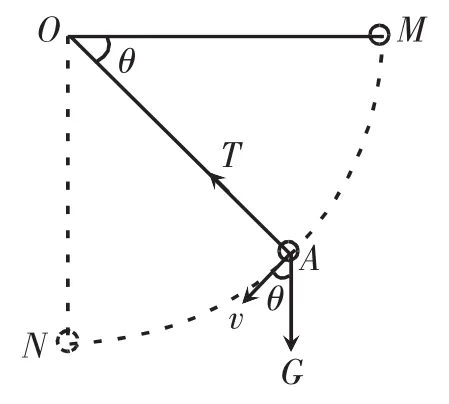
图11 例6解析1图示

小球从M点摆到A点的过程中由机械能守恒可知:

联立(1)(2)式解得:

本题除了运用不等式求解问题,也可以应用物理原理分析问题找到答案。
解析2如图12所示,以释放点为原点建立直角坐标系。


图12 例6解析2图示
7 总结
在高中物理学习中,选择合理的数学运算方法是高效求解物理问题的关键。同时,我们也要结合高中物理教学要求与高中生的实际数学能力,不能一味地把所有物理问题数学化,譬如例6向我们展示了只有抽象的物理分析与合理的数学工具相结合,才能事半功倍。
