辩证思想在高考数学命题中的渗透

侯飞建

(江苏省如皋市第一中学，江苏如皋，226500)

高中数学教育教学的目的是培养学生的核心素养，提升学生通过数学学习并利用数学思维，数学知识来认识世界和解决问题的能力.不难发现高考这种具有极强选拔性功能的考试，在强调数学基础知识的理解与掌握的基础上，明显将辩证唯物思想在试题中进行了合理与有效的渗透.高考数学真题中辩证思维的渗透也是对学生能力考查的一个体现.

1 “动”与“静”

从马克思主义物质观来看，运动是物质的存在形式和固有属性，是指宇宙间所发生的一切变化和过程；静止是指相对某一参照系，事物没有发生特定的变化或者事物的根本性质不变.从辩证思想视角来看，“动”与“静”是密不可分的，运动是绝对的，是静止的一般状态；而静止是相对的，是运动的特殊状态.任何事物都是运动和静止的统一，“动”中有“静”，“静”中有“动”.

( )

分析：根据题设条件，利用“点P，Q均在C上，且关于y轴对称”这两“动点”变化规律，化“动”为“静”，合二为一，以“静止”状态下“点P，Q重合于上顶点B(0，b)”这个特殊位置的选取来分析与解决问题.

解析：已知A(-a，0)，结合点P，Q均在C上，且关于y轴对称，取特殊位置，化“动”为“静”，使得点P，Q重合于上顶点B(0，b)，

故选择答案：A.

点评：本题借助题设背景下两“动点”的运动过程与变化规律加以特殊位置的相对“静止”状态化处理，化“动”为“静”，实现辩证思想的美妙应用.在解决一些平面几何、解析几何、立体几何等相关问题中，经常借助“动”与“静”的辩证思想并加以巧妙应用，引导学生对哲学的“动”与“静”进行思考，感受试题中的哲学辩证美学意义.

2 “整体”与“局部”

从辩证思想视角来看，任何事物都有其“整体”和“局部”内涵，而且“整体”和“局部”二者之间既相互区别又相互联系，“整体”往往处于统率的决定性地位；而“局部”同时制约着“整体”，甚至在一定条件下关键部分的性能对“整体”起着决定的作用.

( )

A

B

C

D

分析：根据题设条件，先考虑整体性质，结合函数的奇偶性的定义来合理排除相应的选项；再考虑局部特点，借助特殊值所对应的函数值正负情况来进一步排除相应的选项，进而“整体”与“局部”相统一，本题得以正确判断.

解析：由于函数y=f(x)=(3x-3-x)cosx，

可知f(-x)=(3-x-3x)cos(-x)=-(3x-3-x)cosx=-f(x)，则知函数y=f(x)是奇函数，其图象关于坐标原点对称，由此可以排除选项B、D；

选取特殊值x=1，可得f(1)=(31-3-1)cos 1>0，由此可以排除选项C；

故选择答案：A.

点评：该试题以函数的图象判断的创设，引导学生从函数的奇偶性的整体性质来分析，并借助局部的情况来综合，两者有机结合，巧妙应用，合理引导学生养成借助“整体”与“局部”之间变化与统一的辩证思想解题以及看待生活中的问题的习惯，引导学生既要树立“整体”的全局观念，寻求最优目标，又要搞好“局部”细节，使整体功能得到最大的发挥.同时也从更深层次引导青年学生在思考与解决问题时，既要从全局高度进行大方向的把握，也要从细致到点的缜密视角合理分析，从而做出正确的最佳决策.

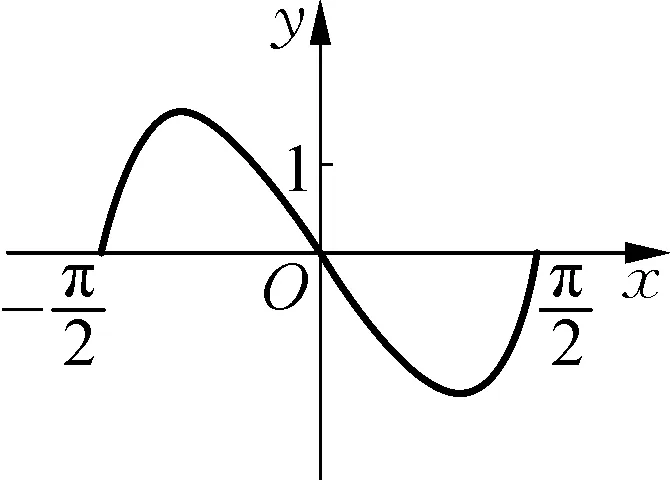
3 “变”与“不变”

从事物运动发展的辩证视角来看，“变”与“不变”两者之间相互依赖、相互包含，并在一定条件下可以实现相互变形与转化.在看待与处理问题时，要合理把“变”与“不变”的两面性有机统一起来，认识与把握“不变”中有“变”，“变”中有“不变”，形成一个和谐统一的整体.

( )

A.tan(α+β)=1 B.tan(α+β)=-1

C.tan(α-β)=1 D.tan(α-β)=-1

分析：根据题设条件，利用两个变角的“变”与一个三角函数方程的“不变”的辩证思维关系来创新设置，借助三角恒等变换公式的综合与应用，合理推导出相应的两变角的和或差的正切值这一“不变”的元素，实现“变”与“不变”的和谐统一.

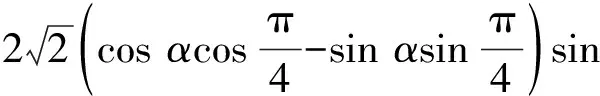
则有sinαcosβ-cosαsinβ=-cosαcosβ-sinαsinβ，即sin(α-β)=-cos(α-β)，

所以tan(α-β)=-1，故选择答案：D.

点评：该题通过正确利用两角和与差公式对复杂角与简单角之间进行“正向”与“逆向”变形，通过“变”与“不变”的关系来实现问题的分析与解决.对于“变”与“不变”的辩证思想，基本实现运动与静止、变量与常量等一些辩证统一体之间的转化与应用，有助于引导学生从哲学角度辩证地看待数学问题，提高数学思想高度，提升数学思维广度.

4 “对立”与“统一”

根据逻辑的辩证思想，任何事物内部都是矛盾对立的统一体，矛盾对立是事物发展变化的主要源泉与动力，而矛盾对立的终点就是统一.否定之否定规律揭示了矛盾对立运动过程中所具有的特点，它告诉人们，矛盾对立运动是生命力的表现，其特点是自我否定、向对立面转化，形成统一体.

例4(2022年高考数学浙江卷·9)已知a，b∈R，若对任意x∈R，a|x-b|+|x-4|-|2x-5|≥0，则

( )

A.a≤1，b≥3 B.a≤1，b≤3

C.a≥1，b≥3 D.a≥1，b≤3

分析：根据题设条件，通过两变参的取值范围的假设，结合自变量的特殊取值情况加以分析，推理分析出与条件产生矛盾对立的结论，产生“对立”与“统一”的转化，结合反证法思维来确定参数的取值范围.

解析：假设a<1，当x→+∞时，可得a|x-b|+|x-4|-|2x-5|=a(x-b)+(x-4)-(2x-5)=(a-1)x-ab+1<0，这与条件a|x-b|+|x-4|-|2x-5|≥0矛盾，故有a≥1；

假设b>3，则当x=b时，可得a|x-b|+|x-4|-|2x-5|=|b-4|-2b+5<0，这与条件a|x-b|+|x-4|-|2x-5|≥0矛盾，故有b≤3；

综上分析，可知a≥1，b≤3，故选择答案：D.

点评：该题从正面直接分析与确定参数取值范围比较有难度，且难以叙述清晰，因此利用找出对立面，再通过逻辑推理发现矛盾的方法，达到应用反证法的目的.反证法思维是应用“对立”与“统一”辩证思想分析与推理问题的一个基本方法，对于问题的解决有时也能起到非常重要的作用.“对立”与“统一”辩证思想引导青年学子在正面难以处理时尝试从对立面入手，化繁为简，从而实现问题的解决.

5 结语

在高中数学教学中，教师要应用发展与联系的眼光看待知识，寻找各部分知识的内在联系，合理构建哲学的辩证思想.一线教育工作者的教学更要结合哲学辩证思想，不能微观片面地只关心学生的阶段性的暂时成绩，而要宏观地、全面地看到学生的整体发展情况，为学生的长远发展铺砖砌石，切实做到传授科学知识时候既要体现科学价值也要渗透人文价值，做到所授内容对学生未来发展有所帮助.