包壳管三维力学建模及其变形分析软件开发

张明， 厉井钢， 刘虓瀚， 卢勇， 朱亚楠

(中广核研究院有限公司反应堆工程软件研究所， 深圳 518000)

燃料棒包壳是防止放射性物质外泄的第一道安全屏障，其堆内性能直接影响核电厂运行的安全性与经济性。因此，燃料棒包壳的变形机理及其数值分析方法一直是反应堆核燃料研究的重点。

燃料棒包壳一般由锆合金[1]制成，在寿命初期由于UO2芯块的密实作用其体积收缩，导致包壳在轴向产生未支撑段，这是包壳蠕变坍塌的先决条件。在反应堆内高温、高压和辐照等耦合作用下，未支撑段包壳会逐渐向内蠕变，最终坍塌失效，蠕变是包壳坍塌的根本原因。包壳坍塌会造成局部热点影响冷却剂流道，或者使得临近燃料棒或导向管弯曲，影响反应堆运行安全。中国压水堆燃料组件设计标准[2]规定：包壳要满足自立条件，且不能发生蠕变坍塌。由于包壳的服役工况复杂，难以直接观测其变形状态，因此需要对包壳的变形和应力进行建模计算，常见分析方法包括理论解析建模和开发专用软件求数值解。

包壳管的理论建模可追溯到1959年，Hoff等[3]研究了无限长薄圆柱壳在均匀外压作用下的稳态蠕变行为，但未考虑包壳管的弹塑性变形和瞬态蠕变。Bargmann[4]通过考虑弹性变形扩展了Hoff的方法，并指出包壳的弹性变形会极大降低包壳寿命。Nishiguchi[5]假设应力沿着壁厚均匀分布，并给出无限长高温气冷堆加热管的蠕变坍塌临界时间。以上研究只限于模态二失稳，并未考虑失稳后的后屈曲行为。随后，严爱民[6]提出了高温和外压作用下有限长圆柱壳的多模态蠕变失稳解法；谢旭华[7]开展了无限长夹心壳的后屈曲研究；Xue[8]研究了无限长圆柱薄壳的局部失稳现象，并给出了其后屈曲解；卢勇等[9]基于商业有限元软件ABAQUS研究了三维燃料棒包壳管的变形和坍塌行为。

虽然理论建模可得到包壳管蠕变失稳和后屈曲的解析解，但理论建模只适用于边界规则、几何模型简单的问题，对于堆内变形行为复杂的包壳管，通常开发专用数值软件计算包壳的堆内状态，并判断其是否符合安全标准。常见的包壳变形分析软件包括BUCKLE[10]、COLAPX[11]、COVE-1[12]、CEPAN[13]和FROCO[14]等，以上软件采用无限长管假设(即平面应变假设)和截面上的对称假设，在蠕变坍塌变形计算和临界寿命评估方面存在以下不足。

(1)均基于平面应变假设，是一种二维的力学模型，其几何模型为无限长管，这在变形分析中会产生较大误差，虽然COVE-1[12]、CEPAN[13]和FROCO[14]考虑了对有限长管的修正，但计算误差仍然较大。

(2)COLAPX[11]、COVE-1[12]、CEPAN[13]和FROCO[14]在截面内采用对称假设，只分析1/4模型，故只能分析圆管变为椭圆管的模态二失稳，而实际包壳未支撑段为有限长度，一般会发生多模态失稳[8]，以上软件无法准确模拟。

(3)在数值计算方法方面，BUCKLE[10]、COVE-1[12]和CEPAN[13]采用有限差分法，计算精度依赖于空间和时间步长，大时间步长的计算结果精度受限；FROCO[14]采用矩阵变换法将计算域离散为许多小结块，未考虑结块之间的相互作用，难以精确得到包壳的变形和应力状态。综上所述，现有计算软件的基本假设和计算方法不尽合理，难以精确计算包壳的应力和变形，也难以准确预测包壳的堆内状态。尽管商业软件在包壳管蠕变变形计算中可以被采用[9]，但其仍不如以上专业软件应用广泛和计算方便。

针对现存软件的不足，亟须研究燃料棒包壳的三维变形机理，即建立热-辐照-力等多物理场耦合作用下的包壳模型，并开发出高精度的专用计算软件。现基于连续介质力学力学理论建立包壳管的控制方程，引入相应的蠕变本构关系，并开发基于有限元的包壳管三维变形数值计算方法。通过与商业软件ABAQUS结果的对比来验证本软件的正确性，并计算真实燃料棒包壳的堆内变形。

1 方法

1.1 控制方程

直接建立包壳管的三维几何模型，无需要求包壳管满足平面应力/应变假设。笛卡尔坐标系下一般弹性体的力学控制方程如下。

(1)平衡方程

(1)

式(1)中：σ为应力；x为坐标，i,j=1、2、3分别表示x、y、z方向。式(1)展开为3个方程。

(2)几何方程

(2)

式(2)中：ε为应变；x为坐标；u为位移。式(2)展开为6个方程。

1.2 弹性本构关系

对于弹性体，要想计算出其位移，必须给出弹性本构关系，这里假设包壳管在弹性阶段为线弹性材料，其应力应变关系符合广义胡克定律，即

σij=2Gεij+λεkkδij

(3)

式(3)中：G=E/[2(1-ν)]为剪切模量；λ=Eν/[(1+ν)(1-2ν)]为体积模量，E为弹性模量，ν为泊松比；εkk为体积应变。式(3)包含6个方程。

一般地，弹性力学方程式(1)～式(3)共包含15个方程，需要求15个未知数，分别为应力6个、应变6个和位移3个，因此以上3组方程是封闭的方程系统。引入包壳管的蠕变本构方程，增加方程的同时也增加了蠕变相关的未知量，故方程系统还是封闭、适定的。

1.3 蠕变本构关系

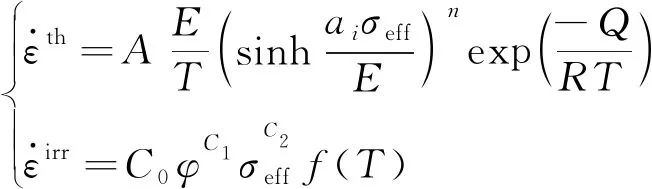
(4)

式(4)中：σeff为等效应力；T为温度；φ为中子注量率，其他参数的取值见表1。参考塑性力学理论的Prandtl-Reuss流动法则，将等效蠕变应变流动到各个方向，即

表1 蠕变本构模型中的材料参数[15]

(5)

式(5)中：Sij为偏应力。

1.4 有限元计算方法

以上方程不仅个数多，而且涉及蠕变引起的材料非线性，无法直接求解，故对以上控制方程进行有限元离散。将有限长的包壳管离散为六面体，采用八节点线性等参元建模。为了兼顾效率和精度，经网格收敛性测试后包壳管径向、环向和轴向的网格数分别为3、40和7个，总网格数为840，结构化网格划分如图1所示。

图1 包壳管三维网格

八节点等参元的形函数为

(6)

式(6)中：ξ、η、ζ分别为母单元上的3个方向的坐标值。

单元内任一点的坐标和位移可以用8个节点的相应量插值表示为

(7)

式(7)中：带有上角标“0”的量均表示结点的值。

将应变张量写为Voigt向量的形式，并把式(7)中位移代入几何方程[式(2)]，则应变向量为

ε=Bu0

(8)

式(8)中：B为应变矩阵。

应力的向量形式由式(3)得到，即

σ=Dε=DBu0

(9)

式(9)中：D为弹性矩阵。

将蠕变应变看作初应变，忽略重力引起的体积力，根据虚功原理，可得有限元方程为

Keu0=fl+fc

(10)

Ktu0t=flt+fct

(11)

通过高斯消去法或超松弛迭代(successive over-relaxation, SOR)法即可计算t时刻的位移。下一时刻t+Δt先由式(4)和式(5)计算蠕变应变，得到附加载荷列阵，再计算载荷向量，重新求解式(11)即得到下一时刻的位移，以此类推直至燃料棒包壳的寿期末。

1.5 包壳失效准则

为了预测包壳管服役状态，并判断其是否失效，需要建立包壳管的蠕变坍塌准则，拟采用以下的失效准则。

(1) 最大屈服应力准则。当应力达到包壳管的屈服应力时，认为包壳失效[2]。

(2) 最大椭圆度准则和最大位移准则。当包壳管上任一点的椭圆度或位移超过限值时，认为包壳蠕变坍塌，椭圆度限值取25%[10]，最大位移的限值取包壳管最小外径的一半[14]。

2 结果与讨论

2.1 测试和验证

为了验证自主软件BINE3D的正确性，拟采用相同的模型与商业软件ABAQUS对比。分别从静力结果和蠕变结果两方面对自主软件进行测试与验证。

2.1.1 静力测试

如图2所示，考虑一边长为1×1×1的立方体，在一个面受到均匀外部拉力1，材料的弹性模量为1、泊松比为0.346，理论结果、ABAQUS和本软件结果见表2。

表2 静力结果对比

图2 单元示意图

对比可看出，软件结果与理论解和ABAQUS结果相同，BINE3D计算结果正确。

2.1.2 蠕变测试

仍采用2.1.1节的模型和参数，同时将蠕变引入，因ABAQUS软件未提供蠕变本构模型[式(4)]，故用经典Norton本构模型代替。Norton蠕变本构的表达式为

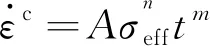
(12)

式(12)中：常数A=0.000 713 05，n=0.8，m=-0.991 5。

BINE3D结果和商业软件ABAQUS结果如图3所示。

图3 单元蠕变结果对比

可以看出，BINE3D结果和ABAQUS结果重合，具有一致性，从而验证了BINE3D计算结果的准确性。

2.2 包壳管结构蠕变坍塌分析

测试和验证表明BINE3D可用于考虑蠕变效应的三维包壳管变形分析。拟进行一真实工况下包壳管的变形分析,包壳管外径为9.75 mm，厚度为0.57 mm，轴向高度为100 mm，弹性模量为绝对温度的函数，即E=1.149×105-59.9T，泊松比为0.346，蠕变本构方程为式(4)，包壳两端位移固定，堆内辐照参数取一典型工况下的温度史、压力史和中子注量史。

包壳截面为均匀圆管时，其最大位移随着时间变化曲线见图4。可以看出，随着包壳管辐照时间的增加，因蠕变产生位移逐渐增加，并且位移的增加速度逐渐减小。到60 000 h，最大位移为0.006 81 mm，包壳结构未失效。

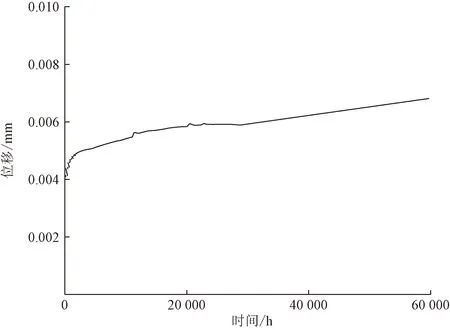
图4 包壳管最大位移随时间变化曲线

不同初始椭圆度下三维包壳管一中部截面(高度h=42.875 mm)的椭圆度随时间变化规律见图5，随着服役时间的增加，初始椭圆度较大的包壳管总椭圆度也较大。随着辐照时间的增加，包壳椭圆度增加速度逐渐减小。辐照60 000 h时，初始椭圆度为0.1 mm的包壳最大椭圆度为3.91%，远小于限值25%，未在服役期间出现坍塌。

图5 包壳管初始椭圆度对总椭圆度的影响

当椭圆度为0.1 mm时，不同时刻包壳管一中部截面(高度h=42.875 mm)外轮廓见图6，随着辐照时间的增加，受外压和持续蠕变导致包壳管的位移越来越大。其长轴向外变形、短轴向内变形。

图6 初始椭圆度为0.1 mm时，包壳管中间截面外轮廓图

三维变形分析软件BINE3D不需对轴向变形做出假设，也无需对包壳的变形进行修正，计算出的结果即为包壳的真实变形。随着辐照时间的增加，长轴和短轴处轴向节点的位移见图7。当辐照时间为60 000 h时，长轴位移呈现出两端为负、中间为正的特点，这是由包壳的三维结构导致的。60 000 h时，长轴最大正向位移和负向位移分别为0.002 88 mm和-0.004 mm。而基于平面应变假设的修正方法无法精确修正出此结果。短轴位移一直为负，即短轴处向包壳内变形，当辐照时间为60 000 h时，最大位移为-0.016 7 mm，短轴位移较长轴大。

图7 椭圆度为0.1 mm时，包壳管长轴和短轴处轴向位置的位移随时间变化

3 结论

基于连续介质力学模型对燃料棒包壳进行了三维力学建模，并采用有限元方法开发出了包壳三维变形分析软件BINE3D，可用于预测包壳的堆内变形行为并揭示包壳的失效机理。主要工作和结论如下。

(1) 基于有限元数值方法开发了燃料棒包壳三维变形分析软件BINE3D，可准确预测包壳三维在堆变形状态。

(2) 包壳的变形速度(主要由蠕变导致)随着辐照时间的增加逐渐减小。

(3) 具有椭圆截面的三维包壳结构，其长轴位移有正有负，而短轴位移均为负且较长轴的变形量较大。

(4) 该软件有望对其他复杂结构的核燃料包壳进行分析。