卷积神经网络在ENSO预报中的应用

李孝涌, 陈科艺, 李熙晨

(1.成都信息工程大学大气科学学院,四川 成都 610225;2.中国科学院大气物理研究所,北京 100029)

0 引言

厄尔尼诺与南方涛动(El Nino-southern oscillation,ENSO)是发生在热带中东太平洋的海温、风场异常现象[1],是热带太平洋主要的气候变率,对全球的气候有深远的影响。海表温度异常作为延伸期重要的下垫面信号,能通过大气遥相关作用对中国的气温和降水造成影响[2],因此,对ENSO的准确预测能提高中长期气候的预测技巧。

目前,ENSO的预报方法主要分为动力方法和统计方法两大类。动力方法采用动力学方程,对海洋、大气、陆地等圈层及其相互作用进行建模,并利用计算机逐步积分,模拟大气的演变,计算出未来的气候状况。欧洲中期天气预报中心(ECMWF)于2017年推出的第五代季节预报系统SEAS5包含了大气、海洋和海冰等部分,是一个耦合动力模型。对SEAS5的评估显示,其在ENSO预报方面继续显示出特别的优势。在预报时效为9个月时,SEAS5对ENSO预报的相关系数在0.7以上[3]。相对而言,统计学模式通过一系列统计学方法,如线性转置模型(LIM)、非线性典型相关分析(NLCCA)、奇异谱分析(SSA)等[4]来预报未来的气候状况。Xue等[5]利用线性Markov模型,采用海表温度、海平面高度和风应力作为预报因子,建立了预报模型。在预报时效为6个月时,其预报相关技巧为0.8。Kondrashov[6]采用多层次回归分析来获得ENSO的随机强迫模型。在预报时效为6个月时,其相关系数超过0.6。

近些年,随着机器学习技术的快速发展和计算机硬件计算速度的不断提高,基于神经网络的预测方法被广泛应用在各个领域,神经网络在气象领域中的应用也正日益受到关注。ENSO作为海洋-大气相互作用的产物,具有明显的非线性特征。而神经网络中引入的非线性的激活函数,使其具备了拟合任意函数的能力[7],从而能够完成非线性回归的任务。

前人在将机器学习用于ENSO预报上已做了诸多有益的尝试。许柏宁等[8]使用序列到序列(Seq2Seq)模型来预测区域SSTA,结果在提前7个月以上的预报上,均方根误差(RMSE)比动力学模式小,但在峰值处误差较大。Dandan He等[9]同样使用了基于卷积长短时记忆神经网络(ConvLSTM)的Seq2Seq模型用于预报Nino3.4指数,其效果比长短期记忆网络(LSTM)、动力学模式的决定性预报和集合预报好。Clifford Broni Bedaiko等[10]使用“气候复杂网络”(Climate Complex Network)提取气象数据特征,用提取得到的特征作为预报因子,使用LSTM预报Nino3.4指数。Ham等[11]以过去3个月的SST和海洋热含量(heat content,HC)为预测因子,训练了一个CNN,该CNN在Nino3.4指数与厄尔尼诺类型的预测上明显优于动力学模型,可提前18个月对ENSO做出预测。

目前,机器学习用于ENSO预报时,与集合预报方法结合比较少。同时各种因素对机器学习预报效果的影响也有待探讨。基于这个原因,文中建立了以深度卷积神经网络(CNN)为基础的ENSO预报模型,通过对照实验确定最佳的模型,并讨论模型在后报实验中给出的结果。

1 资料和方法

1.1 资料简况

用于训练和测试神经网络的数据包括观测资料和模式资料。其中,观测资料来自美国国家环境预报中心(NCEP)提供的全球海洋资料同化系统(global ocean data assimilation system,GODAS)产品。GODAS产品包含海水盐度、海水温度、洋流和海平面高度等多种变量,范围涵盖75°S ～65°N,最大分辨率为1°×1°[12]。模式资料来自第六次国际耦合模式比较计划(CMIP6)。Mckenna等[13]从季节性、强度和频率考察了CMIP6模式对ENSO的模拟能力,结果显示部分模式对ENSO的模拟在季节锁相特征和衰亡阶段存在偏差,多数模式模拟的ENSO频率与观测到的相同,说明CMIP6对ENSO有一定的模拟能力。选用的CMIP6模式包括:AWI-CM-1-1-MR、BCC-CSM2-MR、BCC-ESM1、CanESM5、CESM2、CESM2-WACCM、MCM-UA-1-0、MIROC6、NESM3、SAM0-UNICON。不同CMIP6模式之间的水平和垂直分辨率存在差异,因此使用前需统一进行资料预处理。对于上述所有资料,选取的时间分辨率为逐月数据,选取的资料变量为海表温度以及海水位温。

用于比较预报效果的ENSO历史预报数据由哥伦比亚大学的国际气候与社会研究所提供,包括了各个动力模式和统计模式的Nino 3.4区历史预报数据,时间跨度为2002-2019年。模式包含了动力模式和统计模式。模式的具体情况[22]可参照表1及表2。在诊断海-气相互作用强度时,Nino 3.4指数由NOAA物理科学实验室(PSL)提供,南方涛动指数(southern oscillation index,SOI)由东英吉利亚大学气候研究组提供。

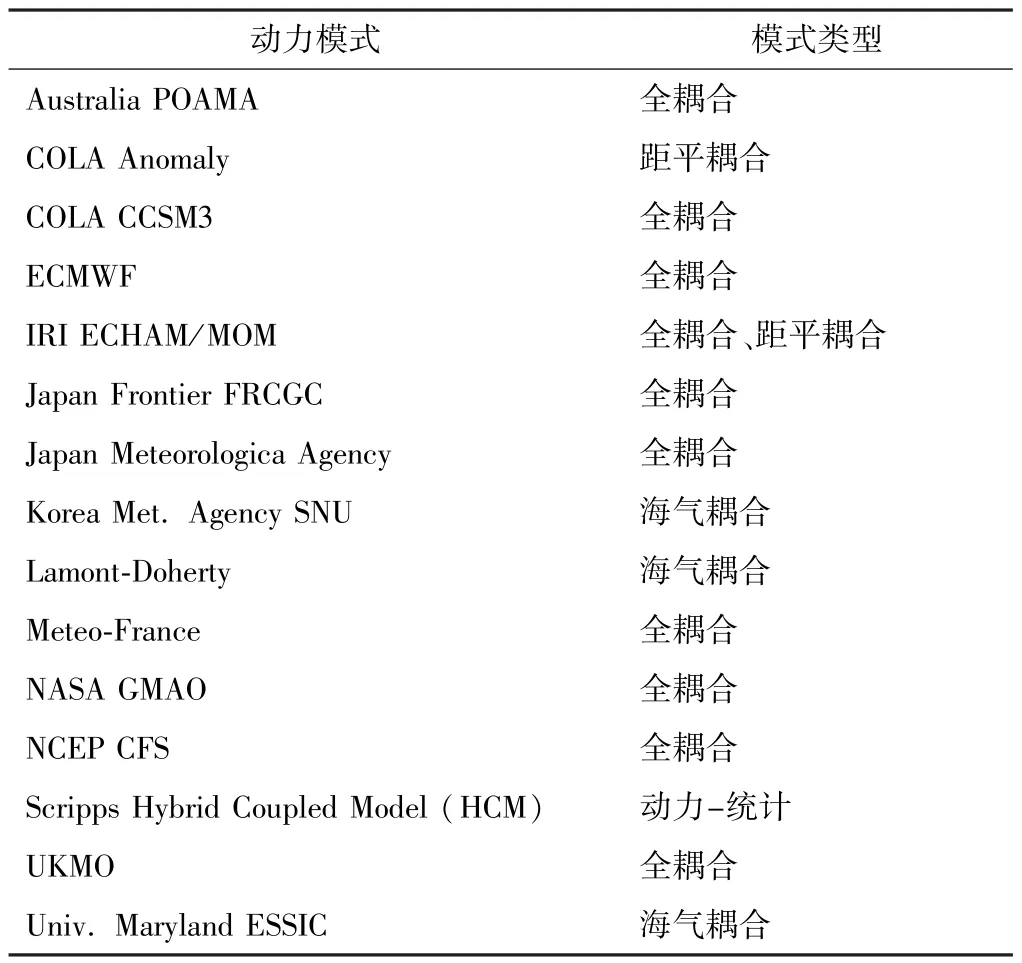
表1 用于比较预报效果的动力模式

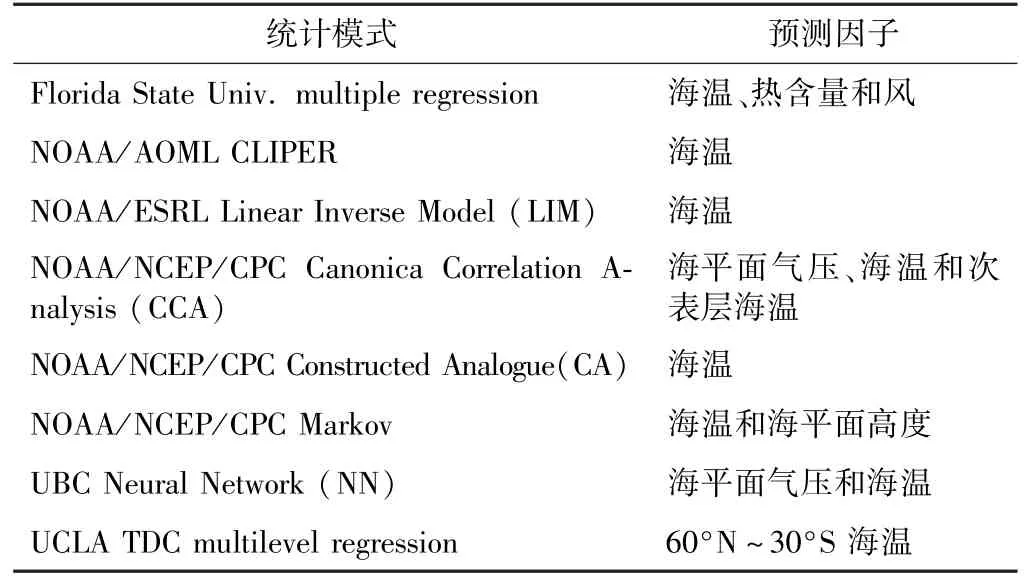
表2 用于比较预报效果的统计模式

2.2 资料预处理

对用于训练神经网络的模式和观测资料,选取的空间范围为中低纬度(60°S～60°N)区域。首先,将资料统一双线性内插到分辨率为2.5°×2.5°(格点数114×49)的格点上,之后计算资料的距平值,然后计算3个月的滑动平均值,最后得到的资料为3个月滑动平均距平值。

海表温度(SST)定义为海洋表层的海水温度。热含量(HC)定义为0～300 m的海水位温积分[14]。Nino 3.4指数是ENSO的指标,定义为Nino 3.4区(170°W ～120°W,5°S～5°N)的纬度加权平均海温的距平值[15]。

2.3 神经网络介绍

使用基于卷积神经网络(CNN)的深度学习架构。CNN作为神经网络的一种类型,能有效提取图像中包含的特征,因此被广泛应用在涉及图像处理(如图像识别、目标检测等)的领域[16]。对气象数据来说,可以把某时刻某要素的分布场视作一张图像,将其作为CNN的输入。用CNN来解决,实际上就是全球海洋要素场与未来几个月Nino 3.4区海温的非线性回归问题。

CNN中包含卷积运算和下采样运算。卷积运算可表示为

另定义代价函数:

其中,C为代价函数的损失值,是实际值与预测值之差,是权重w和偏置b的函数。优化目标是寻找代价函数的最小值,即用梯度下降法寻找使C最小的w,b。

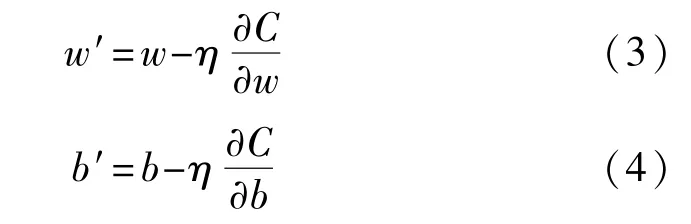
其中η为学习率。训练神经网络时,利用式(3)、(4)可迭代更新权重w和偏置b。

所用的神经网络结构包含2个输入和9个输出。输入1为近3个月全球中低纬度区域(60°S～60°N)的海表温度(SST)距平和海洋0～300m热含量(HC)距平;输入2为近3个月的Nino 3.4指数;网络的输出为未来9个月Nino 3.4指数的预测值。

ENSO是海气相互作用的结果,但相比于大气,海洋存在巨大的热惯性,运动变化有缓慢性和持续性的特征,同时其本身也能反映一定大气环流变化的信息。Ham等[11]的实验证明仅使用海洋的数据是可行的。基于此,文中同样使用海洋的数据作为输入。预测Nino 3.4指数时,有必要特别考虑近3个月的Nino 3.4指数的变化。尽管输入1(中低纬SSTA)包含了Nino 3.4海温的信息,仍将Nino3.4海温单独作为另一个输入,这样可以使模型更好地利用过往Nino 3.4指数的信息。另外,考虑到多数统计模式都采用近3个月的气象要素作为输入,为了方便比较在同一情况下的效果,文中神经网络的输入同样为近3个月的资料。

神经网络的详细结构参见表3。其中,v为变量个数,在对照实验中,有只输入SST和同时输入SST和HC两种情况,因此v的取值为1或2。t为输入时间步数,实验中取3个月。

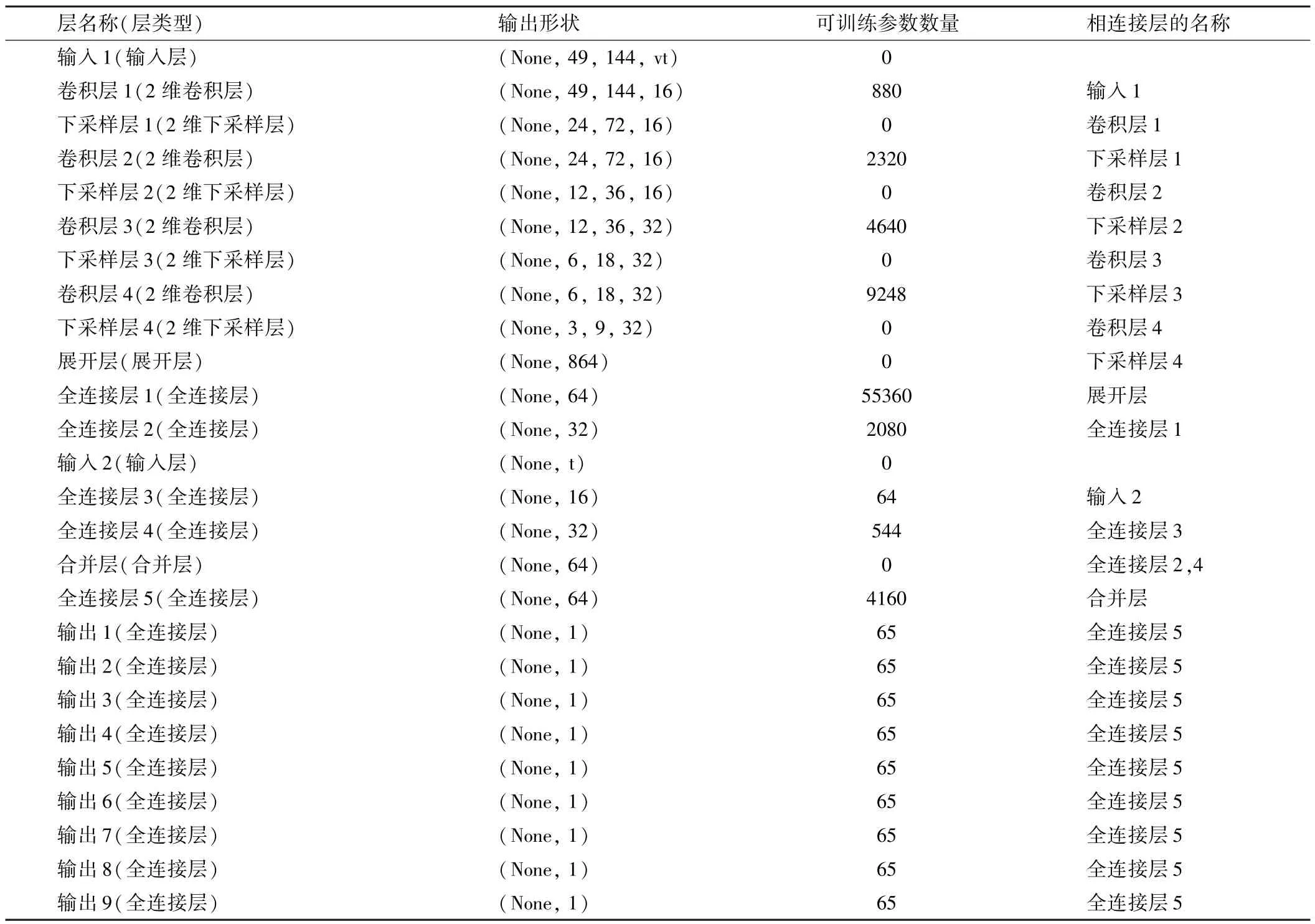
表3 采用的神经网络结构

神经网络中的卷积层起到提取特征的作用,下采样处理则能通过取最大值保留卷积层提取出来的最明显的特征。通过卷积运算和下采样运算,得到的特征图的尺寸被不断缩小。相对而言,卷积核的感知范围不断扩大。因此,采用卷积神经网络的结构能够从全球气象要素场中提取小尺度到大尺度的各个不同尺度的特征。

2.4 实验设计

为研究不同算法、资料和变量对模型预测效果的影响,设计了如下的对照试验,除对照变量外,其余条件保持一致。在下述条件下训练神经网络,当代价函数给出的损失值C不再有明显下降时,则认为神经网络模型收敛,训练已完成。此时终止训练,并将模型用于后报实验中以检测模型的效果。

对照实验一分为两组,区别在于使用算法的不同。首先在保持训练集一致的情况下,引入50个模型分别训练。由于神经网络的初始权重是随机赋值的,最终得到的50个模型略有不同。该实验的其中一组在做预测时,依次使用每一个网络单独做预测(下称单一模型),共预测50次。评价单一模型时,最终结果取这50次预测效果的平均。该实验的另一组则共同将这50个模型输出的平均作为结果,使用多个模型做预测的做法在机器学习领域又被称为集成学习,在时间序列预测上应用广泛,前人的研究显示采用这种方法对改进预报结果能起到一定效果[17-18]。集成学习与数值预报中的集合预报的思路相似,不同之处在于集合预报中的各子成员的初始扰动需要用各种方法专门确定,而集成学习是通过训练时引入随机性来产生不同的子成员。下文将采用集成学习的模型称为集合模型。

对照实验二分为三组,区别在于使用资料不同。其中组一采用实际观测资料,组二采用模式资料,而组三同时采用观测资料和模式资料。当同时使用观测资料和模式资料训练网络时,采取了机器学习领域中迁移学习的方法,即先用模式资料训练神经网络,在此基础上再用观测资料对神经网络进行微调。做迁移学习时,虽然模式资料不能完全反映真实海洋的变化,但是经过模式资料的训练,神经网络可以先收敛到较接近真实的情况,之后,再用观测资料训练这个神经网络,神经网络给出的情况就会更加接近真实结果。迁移学习结合了模式资料数量多和观测资料质量高两个优点,克服了过往仅采用观测资料,数据集不够大的问题。实验二使用观测资料时,为了正确评估模型的效果,将观测资料划分为训练集(1980-1996年)和测试集(1996-2019年)。其中训练集仅用于训练模型,验证集在后报实验中用于评估模型效果。

对照实验三分为两组,区别在于输入变量不同。其中一组只采用SST作为输入,另一组同时采用SST和HC作为输入。

除实验二因需比较不同资料的情况,没有完全使用全套资料外,实验一和实验三均同时使用了模式资料和观测资料,并同样采用了迁移学习的方法。最终选取在上述实验中效果最佳的模型进行讨论。

3 实验结果分析

图1给出了各组实验下模型的预报技巧,这里使用预报值与观测值之间的Pearson相关系数作为后报实验中模型准确度的度量[19]。从图1可以看到在任何条件下,相关系数均随着预报时效的增加而下降。这一点很好理解:海洋运动表现出混沌的特性,初始的微小误差会随时间放大,从而影响长时间的预报效果。

图1 不同方法下模型的预报技巧(误差线表示其他变量变化时,预报技巧的变化范围)

图1(a)展示了单一模型和集合模型的效果差异。可以看到,集合模型的引入对于效果有明显改进,能提升预报的相关系数,而且预报时效越长,提升越明显。这证明了采用集合模型确实能较大程度地提升预报效果。

图1(b)展示了使用不同资料对模型效果的影响。可以看到同时使用模式资料和观测资料时,模型的表现优于单独使用一种资料。另外可以看到,对于1～7个月(短中期)的预报,仅用模式资料比仅用观测资料的效果好,而对于8个月及以上(长期)的预报,则是仅用观测资料的效果更好些。这说明模式资料主要改善的是短中期预报,而观测资料改善的则是长期预报。

图1(c)展示了仅用SST和同时使用SST和HC时效果的差异。引入HC之后,对结果有负面的影响。理论上,HC包含了海洋更深层次的信息,应该能够改进预报的效果,特别是能够减轻春季预报障碍[20]。但对神经网络来说,增加输入的数据量并不是总能提高输出的效果。例如,Jonathan等[21]在预报位势高度场时,对比过仅使用500 hPa的单层资料和同时使用700 hPa、500 hPa、300 hPa的多层资料的效果,后者并没有表现出比前者更好的改善,研究指出这可能是由于模型没有输入变量的垂直结构信息。另外,虽然HC提供了更多的信息,但在实际观测中,海洋次表层的数据比表层稀缺,以及数值模式对该层次物理过程的刻画能力,这些都有可能导致HC的数据质量不如SST。总之,引入HC后预报效果下降的原因在之后的研究中值得进一步讨论。

对照实验表明,在使用集合模型同时使用模式和观测资料,以及仅用SST数据时,模型的表现最佳。图2展示了神经网络模型与传统动力模式集合平均和统计模式集合平均的预报技巧比较。可以看到神经网络模型的效果优于传统动力模式集合平均和统计模式集合平均,在预报时效为9个月时,相关系数仍可以达到0.7以上。

图2 神经网络、动力模式集合平均和统计模式集合平均的预报技巧

图3比较了在测试时间段(1996-2019年),实际观测的Nino 3.4指数和模型给出的预测值之间的差异。对于短时效的预报,模型能准确给出ENSO发生的时间和强度。随着预报时效增加,相关系数逐渐下降,集合模型成员的发散程度增加,对ENSO事件强度的预报偏小。同时,对长时效的预报,预报的峰值的时间存在滞后现象。这种滞后现象被称为“目标时段滞后”[22],在动力模式和统计模式中都存在,而由于包括本文的模型在内的统计模式常使用近3个月平均作为输入,因此与动力模式相比滞后的情况更加突出[22]。另外,由于采用了集合模型,可以给出成员发散的范围,这在实际业务中具有更多的参考意义。

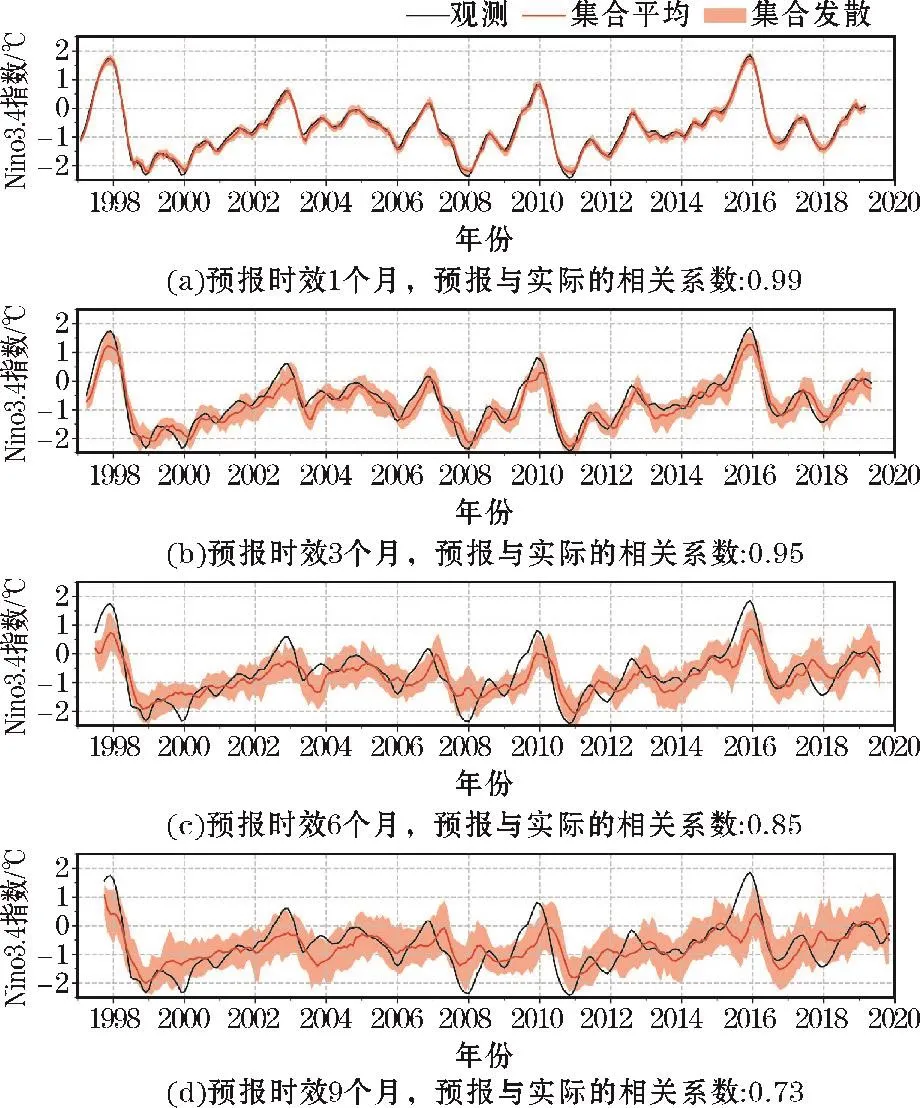
图3 不同预报时效下,观测的Nino 3.4指数、模型集合平均预报和集合成员发散范围

图4给出了在不同的目标月份和预报时效下,模型准确度的变化。除了准确度随预报时效增加而减小之外,还可以发现准确度存在着周年变化。具体而言,在冬春季节预测夏季的情况时,准确率相比于一年中其他时间有明显的下降,这个ENSO预报问题被称为“春季预报障碍”。进一步计算表明,在预报时效为6个月时,集合模型50个成员间的方差在春季最大。这说明集合预报在春季发散最明显、预报的不确定性在春季最大,从另一个角度体现了“春季预报障碍”。

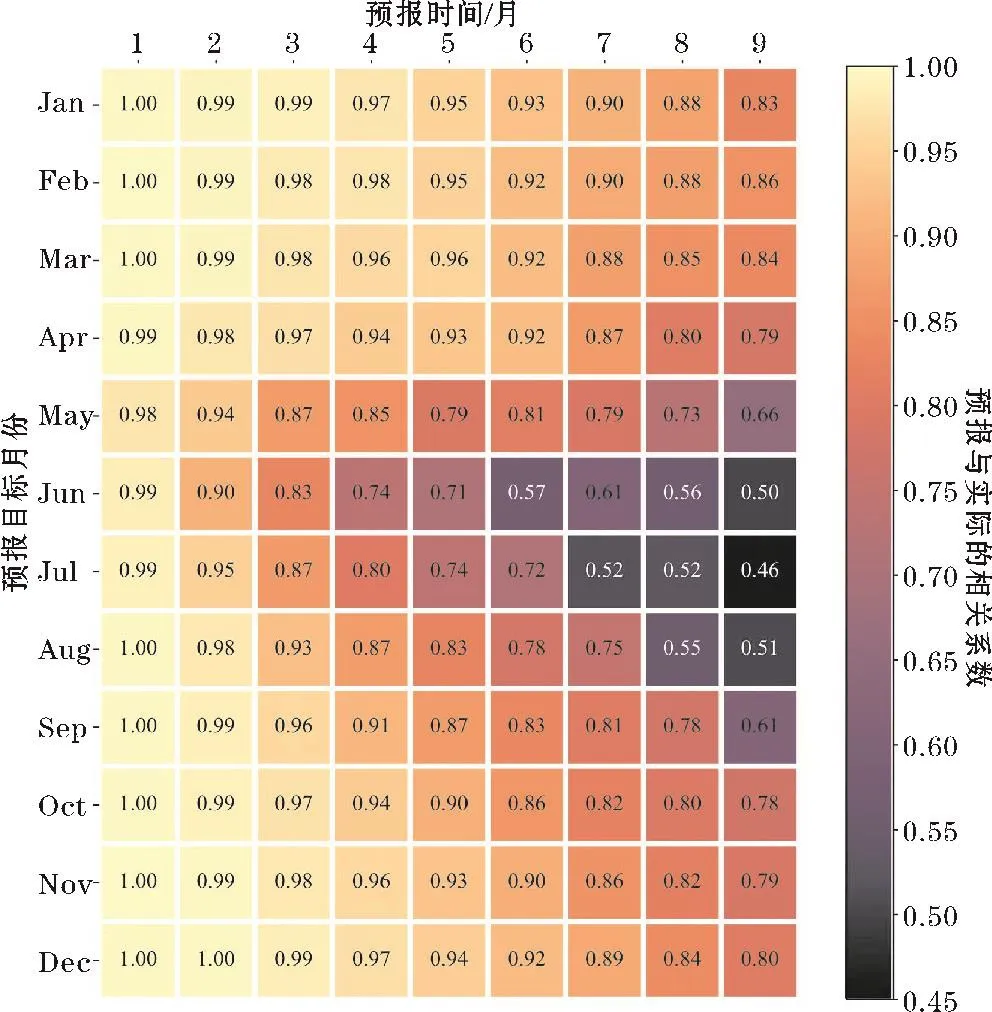
图4 不同的目标月份和预报时效对应的模型的预报技巧

春季预报障碍的存在一般认为和季节循环、ENSO自身性质、初始误差3个原因有关[23-24]。南方涛动指数(SOI)和Nino 3.4指数的相关系数可以表征海-气相互作用强度。计算了不同月份的SOI和Nino 3.4指数的相关系数,发现相关性在春季最低,表明海-气相互作用在春季最不稳定,误差易在春季发展,这从季节循环的角度对春季预报障碍做出了解释。

除了模型预报技巧的年内变化外,本文还研究了预报技巧在年际尺度上的变化(图5)。统计了在预报时效为1～6个月时,模型预报的平均绝对误差(MAE),计算结果显示1～6个月MAE呈现出明显且一致的年际变化。MAE的年际变化指示出ENSO可预报性的年际变化,前人的研究指出这与海-气相互作用的Bjerknes反馈的强度有关[25]。

根据国家气候中心给出的《ENSO历史事件统计表》,将中等及以上强度的厄尔尼诺发生的时间段时间绘制在图上(图5粉红色区域),可以看到在中等及以上强度的厄尔尼诺发生之前,误差会有比较大的增长。结合图3,可以得出这主要是模型在预测时对厄尔尼诺的峰值估计偏小、时间估计滞后造成的。另外在对预报拉尼娜时,误差增大的现象则表现得不明显(图5蓝色区域),呈现出预报误差的不对称性。根据张雅乐等[26]的研究,在ENSO事件冷暖相位,预报误差的增长位相具有显著的非对称性,发展期暖位相预报误差强于冷位相,这解释了预报误差不对称性的现象。

图5 预报时效为1～6个月时,模型预测的平均绝对误差随年份的变化

4 结论与讨论

将神经网络应用到ENSO预报中,利用神经网络预测Nino 3.4区SSTA,并对模型的预报结果进行了讨论。

对照实验的结果表明,采用集合模型的方法不仅能够提高预报的准确度,集合成员给出的发散范围在实际业务中也具有参考价值。数值模式的加入,可以弥补实际观测资料不足的问题。把模式资料和观测资料相结合,可以提高模型的预报技巧。对于预报因子的选择,需要通过实验结果来判断其效果。增加预报因子、扩大输入量不一定能改善预报效果。

文中选择了在多组实验中表现最佳的模型。该模型在时效为1～9个月的后报实验中表现优于传统的统计模式集合平均和动力模式集合平均。对后报实验结果的分析表明,神经网络的预报准确度存在着年内和年际变化。其中,年内变化和“春季预报障碍”有关,年际变化和ENSO可预报性的年际变化有关。

神经网络的预报也存在着一些不足,例如在做长时效预报时,对于ENSO事件峰值存在估计偏小、峰值时间预测滞后的问题。机器学习方法在许多领域的应用都取得了良好的效果,如何将机器学习和气象有机结合值得继续探索。尽管有时机器学习能给出相当好的结果,但与传统方法相比,神经网络是一个只负责输入和输出的“黑箱子”模型。如果能进一步理解神经网络给出这些结果的原因,对于更深地认识其中的物理机制也是有帮助的。