智能车路径跟踪控制器的设计
2022-11-16王月红
王月红, 蒋 涛, 李 平, 周 楠
(成都信息工程大学控制工程学院,四川 成都 610225)
0 引言
随着科学技术的不断发展,自动驾驶技术不断成熟,智能车在生活中得到广泛应用。路径跟踪控制是智能车实现自动驾驶的关键技术之一,其目的是控制智能车的油门、方向盘和刹车等执行机构,使智能车能够按照既定路线行驶[1-4]。
目前主流的路径跟踪控制算法主要有不依靠模型的PID控制算法[5-6]、基于运动学模型的纯跟踪算法[7-8]和基于动力学模型[9]的MPC控制算法[10-12]和LQR控制算法。在这些控制算法中,PID控制算法由于没有考虑车辆的模型所以在实际的应用中效果并不理想;纯跟踪算法虽然是基于车辆的运动学模型进行设计的,但是未考虑车辆的受力情况,所以在道路曲率较大时效果不理想;MPC控制算法虽然是基于车辆的动力学模型进行设计的,但是其需要设置的参数较多,在实际应用中难以调试;LQR控制器是线性负反馈控制器,容易设计。文献[13]设计了智能驾驶车辆LQR路径跟踪控制器,以二轮自行车模型为基础,建立路径跟踪问题状态空间方程,设计了相应目标函数,并对其进行LQR问题的最优求解,获得最佳状态反馈控制率,实现基于LQR控制器的路径跟踪控制。文献[14]基于LQR设计了路径跟随控制器,实现侧向的路径跟随控制,并进行实车实验,验证了算法的可行性。文献[15-17]也对LQR控制在路径跟踪控制上的应用进行了一定的研究。综上所述,文中采用LQR控制理论为基础,设计智能车路径跟踪器。
在上述的研究中,LQR控制器都采用随机设置的Q、R矩阵,这样随机选取的加权矩阵限制了路径跟踪控制器的适用性和精度。LQR控制器的控制效果完全取决于其加权矩阵的选择,然而加权矩阵不能通过数学解析方式得出,只能靠设计者的经验来选择。这样就加大了LQR路径跟踪控制器的设计复杂性。并且,有时随机选择的加权矩阵不但不能实现最优控制,还会增加控制的代价。因此利用遗传算法(genetic algorithm,GA)进行全局搜索,以智能车路径跟踪的横向误差和航向误差作为目标函数选择最佳的加权矩阵,减小LQR路径跟踪控制器设计的复杂性和提高控制器的精度。此外,传统的LQR路径跟踪控制方法未考虑道路的曲率信息,存在稳态误差问题,文中通过在LQR路径跟踪控制器的基础上加上一个前馈控制消除系统的稳态误差。
1 路径跟踪误差动力学模型
1.1 车辆动力学模型
车辆动力学模型反映车辆各个部位的受力情况,对智能车路径跟踪控制具有十分重要的意义。如图1所示,为方便对车辆进行控制,根据受力情况建立车辆的模型。为简化控制只考虑车辆横向和纵向受力情况,并假设前轴和后轴的两个车轮的转角与侧偏刚度相等,汽车后轮不进行转向,并且忽略空气阻力对车辆的影响,将汽车简化为二自由度单车模型。
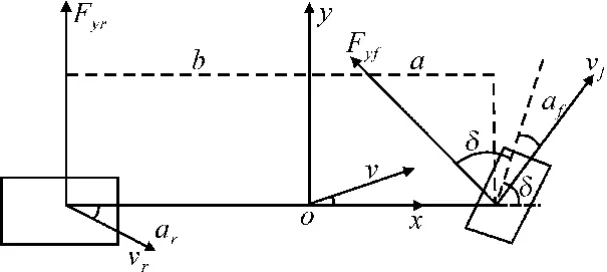
图1 汽车动力学模型
图1中,汽车沿Y轴受力情况和绕Z轴的转动惯量为
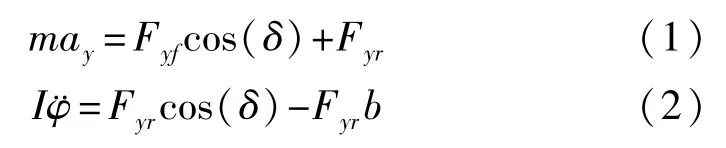
假设δ较小,cos(δ)≈1,那么式(1)、(2)可改写为
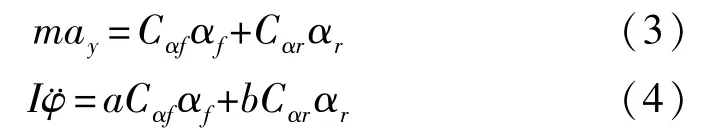


表1 公式符号的含义
1.2 车辆路径跟踪动力学模型
建立了动力学模型还不能直观地看出方向盘转角和车辆横向位移的关系,因此再进一步将车辆投影到自然坐标系下,建立以相对于期望路径的横向误差和航向误差为状态变量的误差动力学模型。
如图2所示,将车体坐标系投射到自然坐标系下,这样可以将车辆的控制解耦成横向控制和纵向控制,降低控制的复杂度。
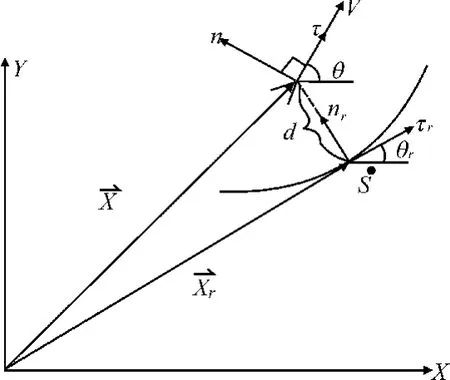
图2 车辆坐标转换
设横向误差为d,航向误差为θ-θr,投影点速度大小为,根据向量的关系可得

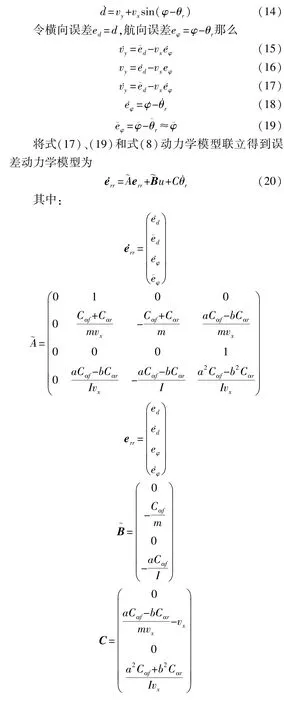
2 LQR控制器设计及其参数优化
2.1 LQR控制器的设计
LQR的控制对象是一个以线性状态空间表达的线性系统,而能量函数为控制对象的状态向量和控制量的二次型函数。LQR的作用在于当系统状态偏离或者还未达到目标状态时,能消耗不多的能量使系统状态向量的各个分量去接近目标状态。利用 LQR控制理论设计路径跟踪控制器,需要先设计一个包含控制对象的状态向量和控制量的二次型函数。一般选取如下能量函数:
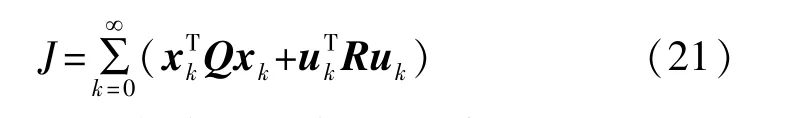
其中,Q和R是LQR控制器的加权矩阵,Q=diag[q1,q2,q3,q4],R=[r],xk为状态量,uk为系统输入量。Q中的元素分别代表对系统状态中横向偏差、横向偏差变化率、航向偏差和航向偏差变化率的重视程度,其值越大,其对应的目标便越快速的靠近目标状态;R中的元素代表对控制量输出的限制,其值越大,代表对控制量输出的限制越大。
由于处理器不能处理连续信号,所以要将误差动力学模型进行离散化处理:

2.2 前馈控制器的设计
在设计LQR控制器时,求解系统的最优解时并未考虑道路的曲率信息,也就是误差动力学模型式(20)中的C˙θr,那么LQR控制器求解出的控制量作用智能车时无论如何都不能使智能车的系统状态达到目标状态。因此在LQR控制器的基础上根据误差动力学模型中的道路曲率信息设计一个前馈控制δf消除系统的稳态误差。加入前馈控制后系统的输入量为

2.3 基于遗传算法的LQR控制器参数优化
由式(21)可知,LQR控制器的效果与其加权矩阵息息相关,这两个加权矩阵的选取直接影响智能车在无人驾驶过程中的路径跟踪效果。但是加权矩阵中的元素并不是越大越好,而要考虑之间的平衡。由于系统状态中横向偏差、横向偏差变化率、航向偏差和航向偏差变化率是影响智能车路径跟踪的主要因素,而LQR路径跟踪控制器中的控制量只有一个前轮转角,所以将加权矩阵R中的元素设置为固定值,考虑用遗传算法优化选择出合适的加权矩阵Q中的元素。
遗传算法是一种模仿自然界物种进化的算法。它将问题参数编码为染色体,再利用迭代的方式进行选择、交叉以及变异等运算交换种群中染色体的信息,最终生成符合优化目标的染色体。
根据系统的横向偏差ed、航向偏差eφ、横向偏差变化率˙ed和航向偏差变化率˙eφ设计遗传算法优化的适应度函数,但是ed、eφ、˙ed和˙eφ的单位不一样,因此除以车辆路径跟踪的性能指标值统一单位,得到遗传算法优化的适应度函数,该适应度函数如下:
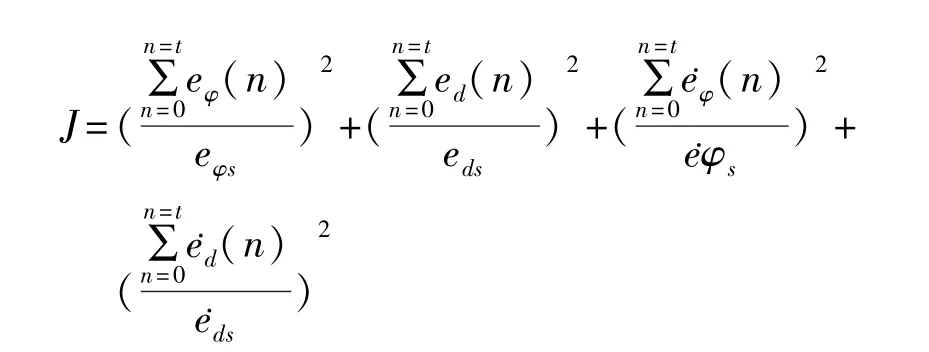
其中,eφs为智能车航向偏差性能指标,eds为车辆横向偏差性能,˙eφs为车辆航向偏差变化率性能指标,˙eds为车辆横向偏差变化率性能指标。
优化算法流程图如图3所示。
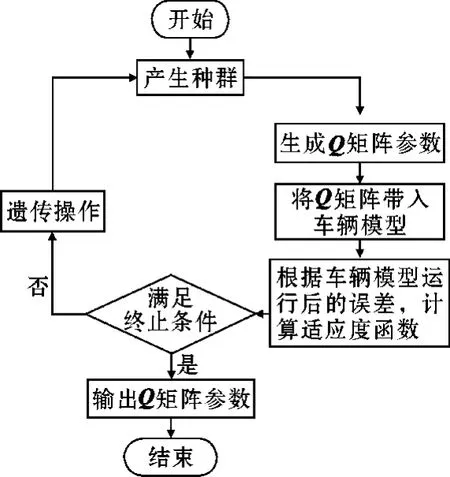
图3 LQR控制器参数优化流程图
首先,随机生成一个种群,种群中的个体即为加权矩阵Q;其次,将加权矩阵Q带入车辆模型中计算偏差;再次,利用偏差计算适应度函数;然后判断是否符合终止计算的条件,若符合条件,退出算法的计算,若不符合,进行遗传操作重复前面的步骤;最后输出符合终止条件的加权矩阵Q。
利用 matlab/simulink仿真,求解出最优的q1、q2、q3和q4参数,遗传算法参数设置如表2所示。

表2 遗传算法参数设置
通过遗传算法优化后,得到的Q矩阵参数为
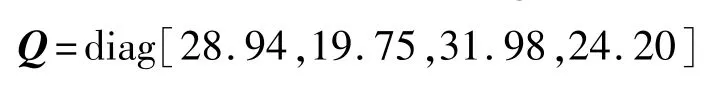
3 仿真实验结果及分析
为验证所设计的GA-FFC-LQR路径跟踪控制器,在carsim/simulink中进行仿真。在carsim中采用的车辆模型参数如表3所示。仿真测试中的道路选择常用的双移线道路和余弦曲线道路,车速设置为固定值10 m/s,由carsim中的控制器进行控制,车辆转角控制由simulink中的LQR控制器解算出来传递至carsim中进行控制。

表3 智能车参数表
3.1 双移线路径跟踪实验
为方便分析本文设计的路径跟踪控制器的性能,同时一起测试了带有前馈控制的LQR控制器(FFCLQR)和LQR控制器的性能。
图4和图5表示了3种控制器在双移线道路仿真中的航向偏差和横向偏差。从仿真的结果中可以看出本文设计的GA-FFC-LQR路径跟踪控制器的横向误差控制在0.1m以内,航向偏差控制在0.05rad以内;FFC-LQR控制在各方面的性能均不如本文设计的路径跟踪控制器;只有单独的LQR控制器在3个控制器中性能最差。
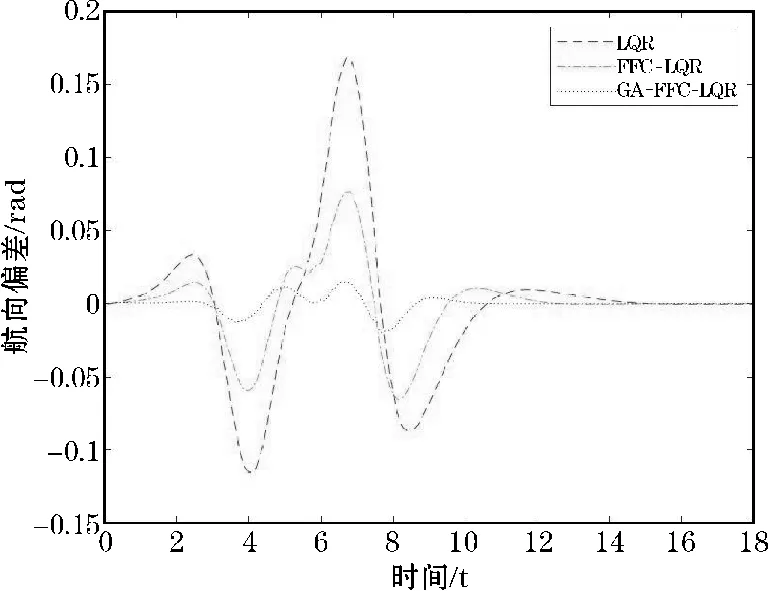
图4 航向偏差(双移线)
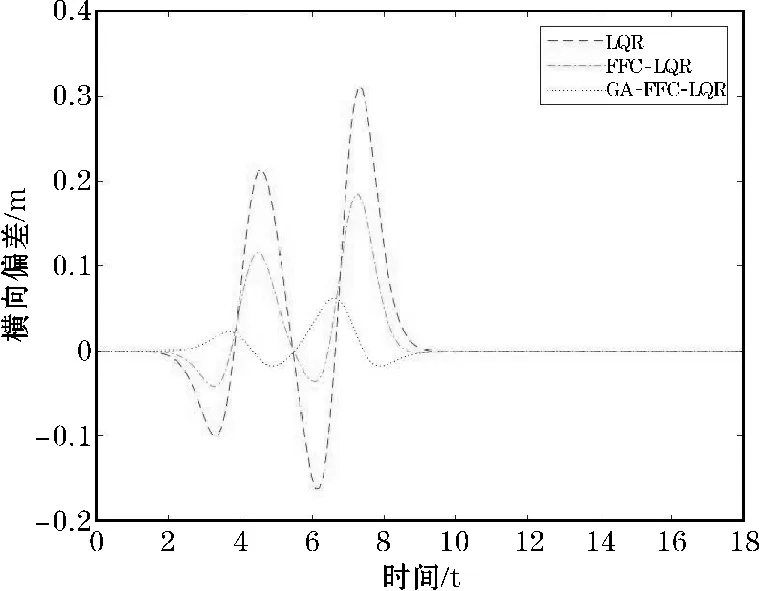
图5 横向偏差(双移线)
在图6的跟踪效果图中,可以明确地看到3种控制器的路径跟踪性能。从图中可以看出本文设计的路径跟踪控制器较为精准的贴合规定路线行驶,FFCLQR控制器也基本能贴合规定路线行驶,但不如本文设计的路径跟踪控制器效果好,单独的LQR控制器在直线时效果与前两种比没有太大的差别,但是在转弯时跟踪精度很差。
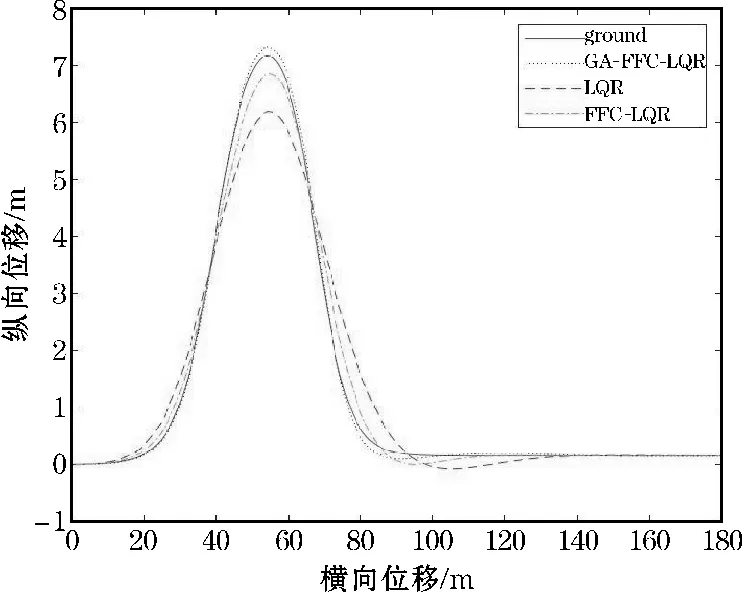
图6 路径跟踪结果(双移线)
3.2 余弦曲线路径跟踪实验
在余弦曲线道路测试实验中,车速仍然设置为10 m/s。仿真的测试结果如图7、图8和图9所示。仿真测试结果显示,基于GA-FFC-LQR的路径跟踪控制器的效果最好,车辆的横向偏差和航向偏差在3种控制器中是最小的,能很好地跟踪目标路径;FFC-LQR控制器的效果比GA-FFC-LQR的路径跟踪控制器效果略差,但基本也能跟踪目标路径;单独的LQR控制器的效果是3种控制器中最差的,尤其在弯道时误差最大。
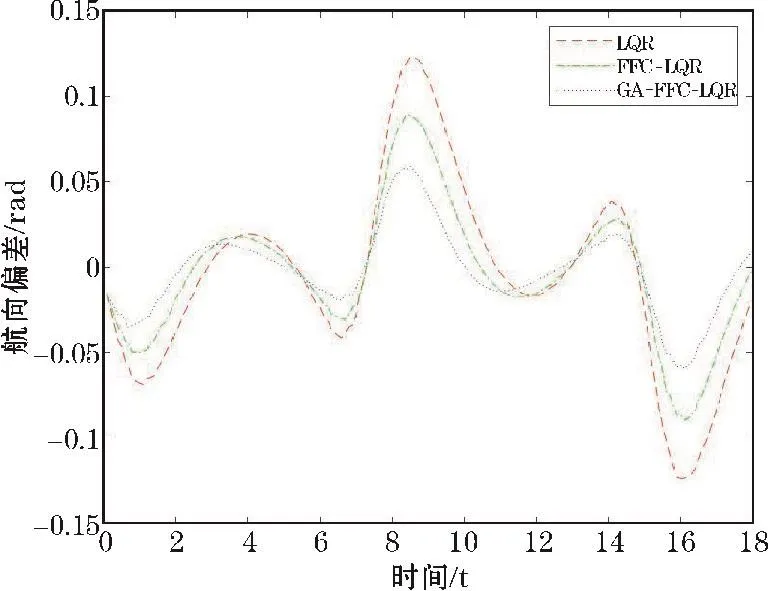
图7 航向偏差(余弦曲线)
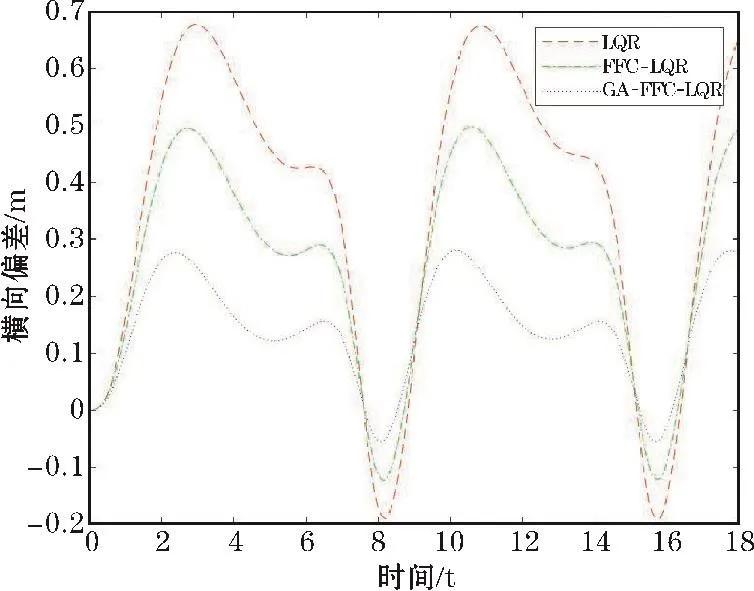
图8 横向偏差(余弦曲线)
4 结束语
针对智能车无人驾驶关键技术路径跟踪控制进行研究。根据车辆的横向和纵向受力情况以及合理假设的基础上建立了二自由度车辆动力学模型,并根据此动力学模型建立了相对于期望路径的横向误差和航向误差为状态变量的误差动力学模型,在此基础上设计了基于LQR控制理论的自动驾驶路径跟踪控制器,同时根据道路的曲率信息加入了前馈控制器来消除系统的稳态误差。然后,对LQR加权矩阵参数进行分析,利用遗传算法的全局搜索能力,以智能车路径跟踪的横向误差和航向误差作为目标函数计算最佳的加权矩阵,减小LQR路径跟踪控制器设计的复杂性和提高控制器的精度。最后,通过carsim/simulink的联合仿真对本文设计的路径跟踪控制器进行仿真实验和对比分析,证明了本文设计的基于GA-FFC-LQR的智能车路径跟踪控制器对目标路径具有较好的跟踪控制效果。
