结合时间映射和卷积神经网络的知识补全
2022-11-16陈新元谢晟祎陈庆强
陈新元, 谢晟祎, 陈庆强, 刘 羽
(1.闽江学院计算机与控制工程学院,福建 福州 350121;2.福州墨尔本理工职业学院信息工程系,福建 福州 350121;3.福建农业职业技术学院实验实训中心,福建 福州 350300;4.福建工程学院信息科学与工程学院,福州 350118;5.福州墨尔本理工职业学院现代教育技术中心,福建 福州 350121)
0 引言
知识图(knowledge graph,KG)中的节点和边分别对应实体和关系,以三元组(头实体,关系,尾实体)的形式编码事实,即(h,r,t),h和t分别为头、尾实体,r为实体间关系,如(Beijing,isCapitalOf,China)。主流知识库如NELL[1],YAGO[2],Freebase[3]等,常用于信息检索[4]、问题回答[5-7]、语义搜索引擎[8]、专家系统和社交网络分析等领域[9]。现有知识库数据不完整[10],知识图谱补全[11]是近年的热点方向之一[12-14],主流思路是学习KG中节点和关系的多维矢量表示,同时保留原有结构信息和知识约束。知识有效性常受时间限制,或仅在特定时段内正确,例如(Donald Trump,isPresidentOf,United States)目前仅在2016-2020年有效;(Barack Obama,presidentOf,USA)仅在2008-2017年有效。部分知识库已开始为事实打上时间标签,如YAGO和Wikidata[15]等。然而主流方法在学习实体嵌入和关系翻译时,常将知识图视作静态,忽略了时间信息,因此相关研究较少;Jiang等[16]提出利用时序信息辅助知识补全,但并非直接将时间整合到嵌入表示中,而是先学习关系间的相对顺序,再在嵌入阶段将关系顺序引入为约束。
文中提出一种基于时间映射和卷积神经网络的嵌入表达技术TSKGC,将时序信息直接纳入事实嵌入学习,旨在提高链路预测的性能表现。TSKGC先将输入的知识图根据不同的时间戳分为多个子图,将实体和关系投影至对应时间戳的超平面上,从而学习携带时间信息的向量表示。主要工作如下:探讨较少涉及的时间敏感性问题,将时间信息集成至三元组的嵌入表示中;将映射三元组的矩阵表示用作卷积神经网络(CNN)的输入,通过多个通道(不同时间节点对应的超平面)的卷积遍历提取事实特征。
1 相关工作
1.1 关系嵌入学习
嵌入学习是知识表达的热门领域之一,常用于知识图谱补全或链路预测,大致分为两类。一是基于距离的平移嵌入方法,通过降低关系平移后的实体向量距离优化嵌入表示,如 TransE[17],TransH[18],TransR[19],TransD[20],STransE[21]和 TranSparse[22]等。 二是基于矩阵化参数的方法,如基于矩阵嵌入的SE[23]认为若三元组有效,头实体在子空间中的映射应接近尾部向量;RESCAL[24]使用双线性模型表示特征和关系间的相互作用;DistMult[25]和ComplEx[26]使用三重积计算三元组得分。此外,NTN[27]使用张量网络提升表达能力;Nguyen等[28]和Toutanova等[29]引入了关系路径;也有研究使用文本信息增强等其他方法[30-34]。
TransE在层次结构的概念树和词嵌入空间中矢量表示的基础上设计模型,将标记边对应的关系映射为平移向量,即vh+vr≈vt,其中vh,vr,vt分别为实体h,t和关系r的嵌入表示。d=‖vh+vr-vt‖p,计算当p取L1或L2范数时三元组得分,该算法相对简单,但在复杂关系三元组上学习能力欠佳。
TransH设计了关系特定的超平面wr,将实体进行差异化投影。本文在此基础上,尝试为时间信息建立超平面以学习知识表达。TransR使用投影矩阵Wr进一步提高表达能力,但计算开销增加。
近年来,CNN广泛应用于NLP[35]领域,代表模型如ConvE[13],使用CNN提取头实体和关系特征,但二维卷积可能导致全局特征丢失。ConvKB[36]在ConvE基础上调整,过滤器尺寸size设置为1×3。
1.2 时间信息嵌入
实体之间的关系基数可分为1-1,M-1,1-M和M-M 4种类别,简单方法在1-1关系上可获得较好的建模结果,而对M-1,1-M和M-M等复杂关系,目前尚无统一的建模标准。部分复杂关系与不同时间节点对应的不同尾实体有关,但主流关系嵌入模型的研究对象多为静态知识图,忽略了对时间维度的分析,因而无法直接对这类关系进行区分。
早期的T-YAGO[37]从Wikipedia Infoboxes的半结构化数据中提取时间信息,使用正则表达式分类;UzZaman等[38]设计了时间提取和表达方案并根据顺序与事实对应;t-TransE[16]在TransE的基础上通过关系排序学习时间感知的嵌入表达;双线性模型Know-Evolve[39]使用RNN捕获非线性时间变化的动态特征;Leblay等[40]使用知识图中静态的辅助信息进行时间嵌入学习;Dasgupta等[41]将时间对应的超平面与实体关系融合;另外有许多研究致力于时间相关的推理[42-43]。文中重点是设计关系嵌入学习模型,以及进一步提高特征提取能力用于知识推理或补全,而非提取时序信息。
2 TSKGC
将时间跨度信息以list形式合并到知识库的三元组中,即(h,r,t,[τs,τe]),τs和 τe分别表示有效期的起始和终止;设定时间点将知识图划分为多个静态子图,每个子图内包括在对应时间点上有效的所有三元组,单个三元组可在多个子图上存在。设图其中i∈1,2,…,N表示离散的时间节点的编号,将其对应到N个超平面,即对于分别有ωT1,ωT2,…,ωTN与之对应。 若 Ti,Ti+1,…,Tm落在三元组的时间跨度[τs,τe],即 τs≤Ti≤Ti+1≤…≤Tm≤τe,则该三元组在上有效,将其投影至这m个超平面,如图1所示,从而保留三元组的时间信息,并通过缩小平移距离优化嵌入表示。
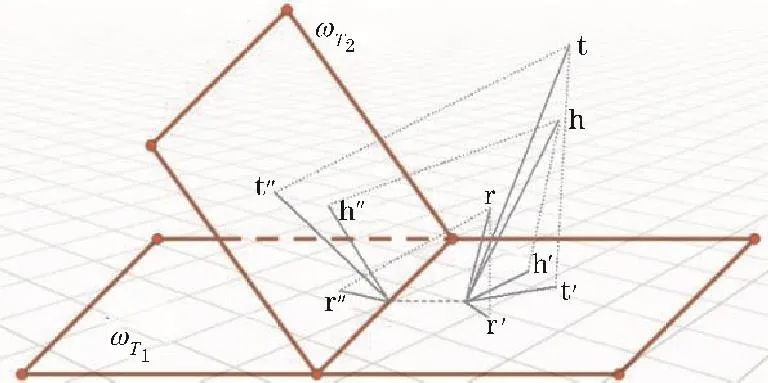
图1 单一三元组映射至多个超平面(多个时间节点内有效)
使用CNN提取三元组嵌入表示的非线性时间演化特征。将对应不同时间节点的N个超平面作为卷积层的多个通道,每通道多个卷积核遍历矩阵,并行提取特征。过滤器的尺寸size和步长stride对特征提取和计算开销影响较大,使用ω∈1×3提取同一维度嵌入向量的特征,步长设置为3,提取全局特征的同时避免无意义的局部特征。特征映射vi为
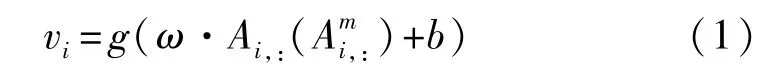
g为非线性激活函数,b为偏置系数,本文使用ReLU。令Ω和τ分别表示ω的卷积核和核数,即τ=|Ω|。卷积层处理后,特征映射的规模可表示为k×m(×τ)。
评分函数f(h,r,t)定义为
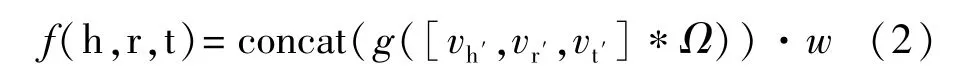
其中,*表示卷积运算,w为权重参数。非线性函数的参数通过关系融合和平移转换得到。流程框架如图2所示。
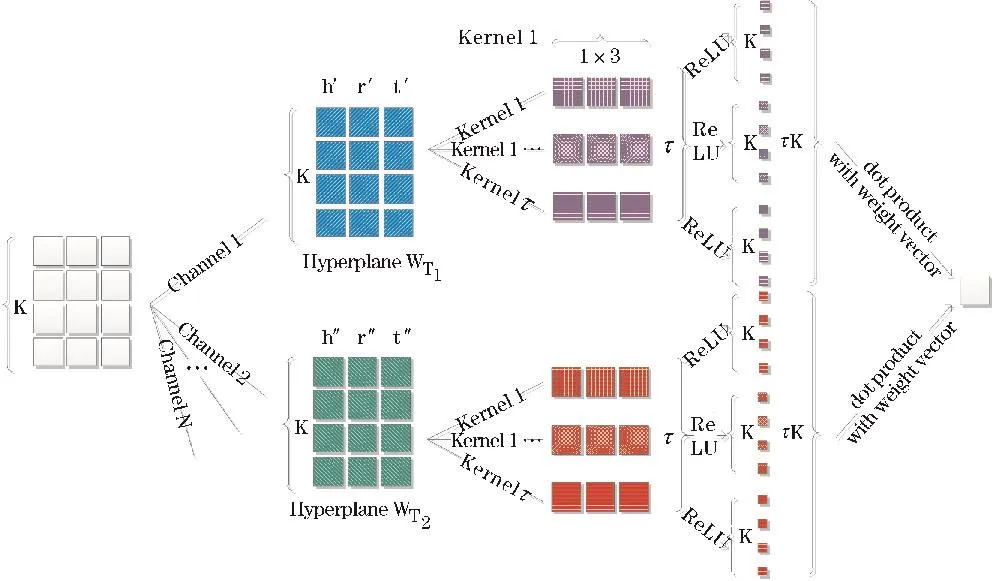
图2 TSKGC的卷积流程

模型算法如Algorithm 1所示,开销控制为O(nek+nrk),与TransE等主流模型在相同量级上。考虑到数据集中的重数关系对实体/关系预测的影响,即一组头实体+关系,或一组头实体+尾实体,可能对应单一或多种尾实体或关系。而单一情况下预测结果应相对较好,因此根据重数关系,为损失函数添加权重系数,使单一取值预测错误的惩罚较高。

无效三元组分为两类:
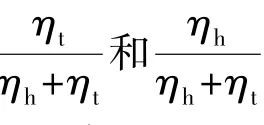
与时间信息相关:随机选择KG中存在的三元组,但修改其时间节点归属。
3 实验结果与分析
在YAGO11k和Wikidata12k数据集上进行链路预测和时间预测[45],将TSKGC算法与TranE、t-TranE、HyTE和ConvKB共4种主流算法比较。YAGO11k从YAGO3[46]数据集中提取包含occurSince和occurUntil标注的事实,选择频数最高的10种关系并去除部分稀疏实体。Wikidata12k的处理流程类似,选择最常见的24种关系。数据集统计信息如表1所示。
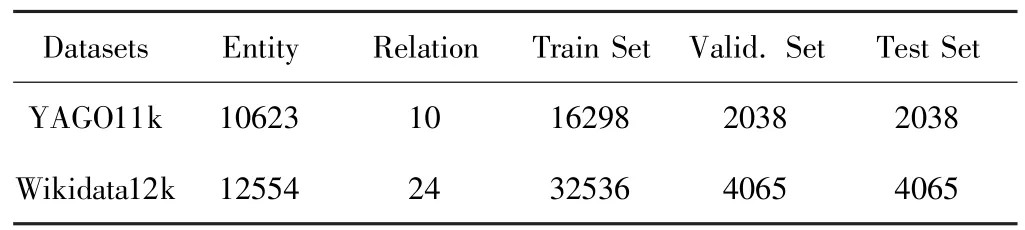
表1 数据集统计信息
3.1 链路预测
链路预测在给定关系和头实体或尾实体的前提下推测丢失实体。文中使用MR(平均排名)和Hits@10(排名在前10位的有效实体的百分比)作为评估指标。实验使用第1类方法创建无效样本,取验证集上Hits@10得分最高的模型用于测试。
TransE的超参数初始化设置如下:k∈[50,100],学习率设定为[1e-4,5e-4],L1范数,margin γ∈[1,3,5,7]。在YAGO11k上,当k=50,学习率=5e-4,L1范数,γ=1时得分最高;在Wikidata12k上,当k=100,γ=3且其他参数相同时,得分最高。
t-TransE的初始设置为k∈[20,50,100],学习率∈[1e-1,1e-2,1e-3],γ1,γ2∈[1,2,4,10],λ∈[1e-1,1e-2,1e-3,1e-4],当 k=100,学习率=1e-3,γ1=γ2=4,λ=1e-2时表现最优。
HyTE的参数初始化设置为:batch size=50k,k∈[50,100,200],学习率∈[1e-2,1e-3,1e-4],L1范数,γ∈[1,2,5,10],当 k=100,学习率=1e-3,γ=5时表现最佳。
TSKGC学习率初始设置为∈[1e-5,1e-4,5e-4],batch size设为[128,256],kernel数 τ∈[100,200,500],轮数 epoch∈[200,500,1000],L2正则化 λ=0.001,使用Algorithm 1中描述的正态分布初始化过滤器,使用Adam优化器,将ReLU作为非线性激活函数。在 YAGO11k上,当k=50,学习率=5e-4,τ=100,使用[0.1,0.1,-0.1]的过滤器分布时表现最佳;Wikidata12k上,当k=100,τ=200,truncated分布,其他参数相同时,得分最优;两个数据集上batch大小都为256,epoch=100。
链路预测结果如表2所示(最优表现设置为黑体,其次设置为下划线),HyTE、ConvKB和TSKGC的MR得分和Hit@10成绩明显优于TransE和t-TransE,而TSKGC成绩总体上相较HyTE和ConvKB又有所提高,说明将时间信息集成到实体关系映射中有助于知识补全,使用多通道卷积网络也利于提取全局特征。
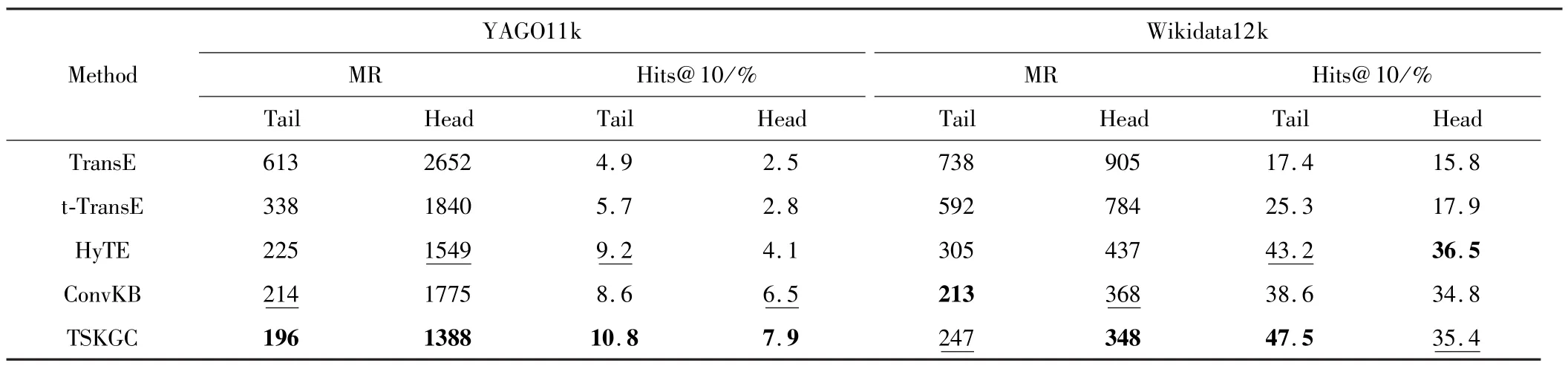
表2 YAGO11k和Wikidata12k上的链路预测结果
YAGO11k相较Wikidata12k,复杂关系的比例更高,而相应Hits@10得分中,TSKGC的优势相比HyTE和ConvKB也较明显,因此将YAGO11k中的三元组按重数关系分为4类,进一步比较 HyTE、ConvKB和TSKGC这3种模型在不同关系上的性能,每类别的预测头/尾实体的Hits@10得分如图3、图4所示。在1-1关系中,无论是预测头部或尾部,HyTE、ConvKB和TSKGC的性能相仿;预测1-M类型的头部和M-1类型的尾部,三者差距也不大;在M-1和M-M类型的头部预测,以及1-M和M-M类型的尾部预测这4种情况下,TSKGC的得分均最高,说明其能更好地识别上述复杂关系。
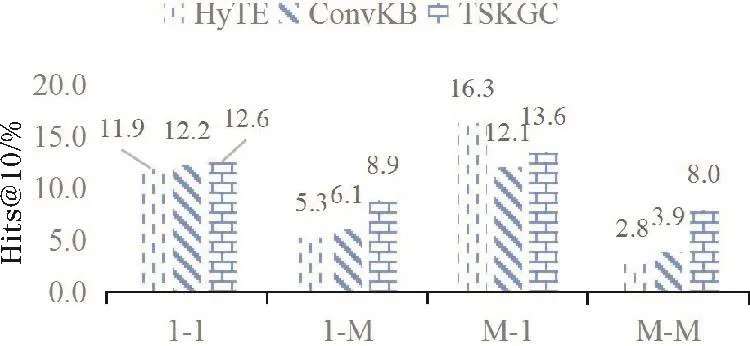
图3 YAGO11k上针对4种类型关系的尾实体预测性能比较(Hits@10)
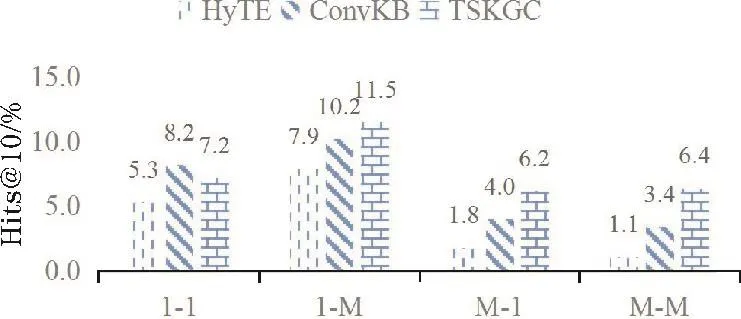
图4 YAGO11k上针对4种类型关系的头实体预测性能比较(Hits@10)
3.2 时间预测
通过超平面映射将时间维度信息直接集成至事实向量,本文模型可用于给定三元组(h,r,t,?)的时间节点预测。实验采用第2类方法创建无效样本,在相同数据集上以相同参数训练、验证并测试;由于其他主流模型无法用于时间预测,故只比较TSKGC与HyTE的表现。实验使用调整的MR指标[41],考察模型的时间预测性能:将三元组的构成元素分别映射至所有超平面上,按概率降序排列,正确时间节点对应超平面的排序越前越好。以年为最小时间跨度,允许稀疏事实的年份合并,阈值设置为500,YAGO11k和 Wikidata12k分别取51和63个时间节点。实验结果如表3所示,可见TSKGC的时间预测能力在YAGO11k中与HyTE基本持平,在Wikidata12k中略有提升。若时间信息完备,该类算法还可扩展为时间范围预测。
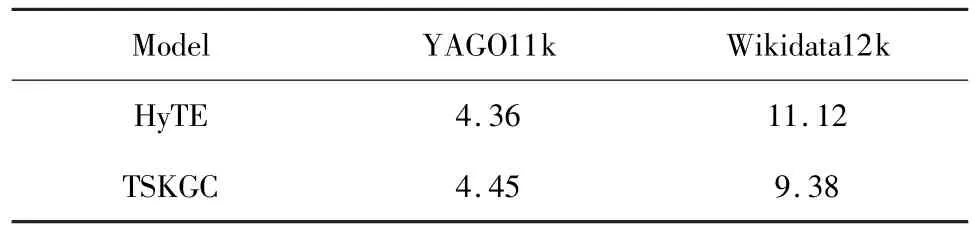
表3 时间预测的MR得分
4 结束语
基于超平面的映射,将事实三元组蕴含的时间信息集成到实体关系嵌入空间中,并进一步结合卷积神经网络,在减小参数规模的同时提取特征并评分,以解决主流算法多在静态图上进行知识表示或推理,没有利用时间信息的局限。实验证明TSKC模型的集成时间信息有助于提高链路预测的性能表现。但实验采用的是带时间信息的数据集,这类数据集难以获取,或手工标注成本较高,因此算法的适用范围需进一步泛化。如根据事实是否携带时间信息,选择不同的嵌入模型并在同一框架内计算其向量表示,以便共享参数,用于知识补全等任务。此外,近年来基于关系路径,以及注意力机制的知识表达和推理模型也取得了较好的成果,计划在未来工作中结合上述思路进一步提升模型性能。
